基本信息
发表刊物
ICML 2025
作者信息
Dilfira Kudrat 1、 Zongxia Xie 1 、Yanru Sun 1 、Tianyu Jia 1 、Qinghua Hu 1
天津大学智能与计算学院
解决的问题
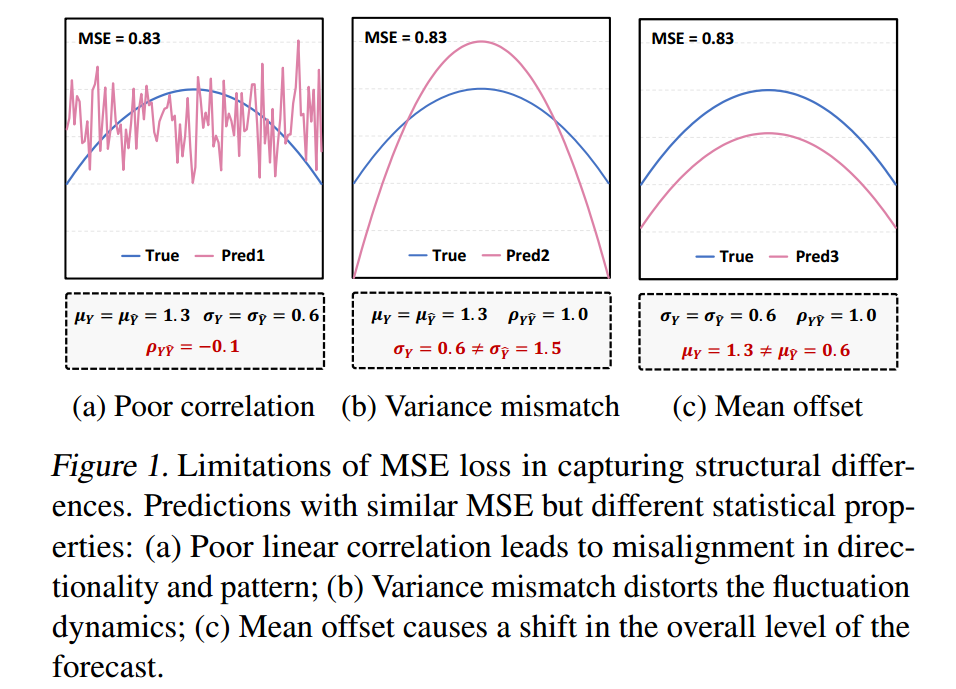
问题(现有方法的局限性)
-
大多数现有的时间序列预测模型 严重依赖于点对点(point-wise)的损失函数 ,例如均方误差(Mean Squared Error, MSE) 。这类损失函数将每一个时间步独立对待,因此忽略了时间序列数据中固有的结构依赖性(structural dependencies) ,这使得模型难以准确捕捉复杂的时间模式。
-
此外,大多数创新方法依赖于整个时间序列的全局比较 ,忽略了关键的局部结构细节。相比之下,我们提出的方法将分片统计特性纳入损失函数,实现了更细粒度的数据结构测量,并为时间序列损失设计提供了一个全新的视角。
解决方案
-
为了解决上述挑战,论文提出了一种新颖的 分块结构化损失(Patch-wise Structural, PS loss)。
-
该损失函数旨在通过在 "块"(patch) 的级别上比较时间序列,从而增强结构对齐(structural alignment)。
-
PS 损失通过利用局部统计特性 (如相关性、方差和均值),来捕获传统点对点损失所忽略的细微结构差异。
-
还能与点对点损失无缝集成,从而能够同时解决局部结构不一致性和单个时间步的误差问题。
简而言之,论文的动机是为了设计一个能够感知和利用时间序列结构信息的损失函数,以弥补传统点对点损失在捕捉复杂时间模式上的不足。
提出的方法
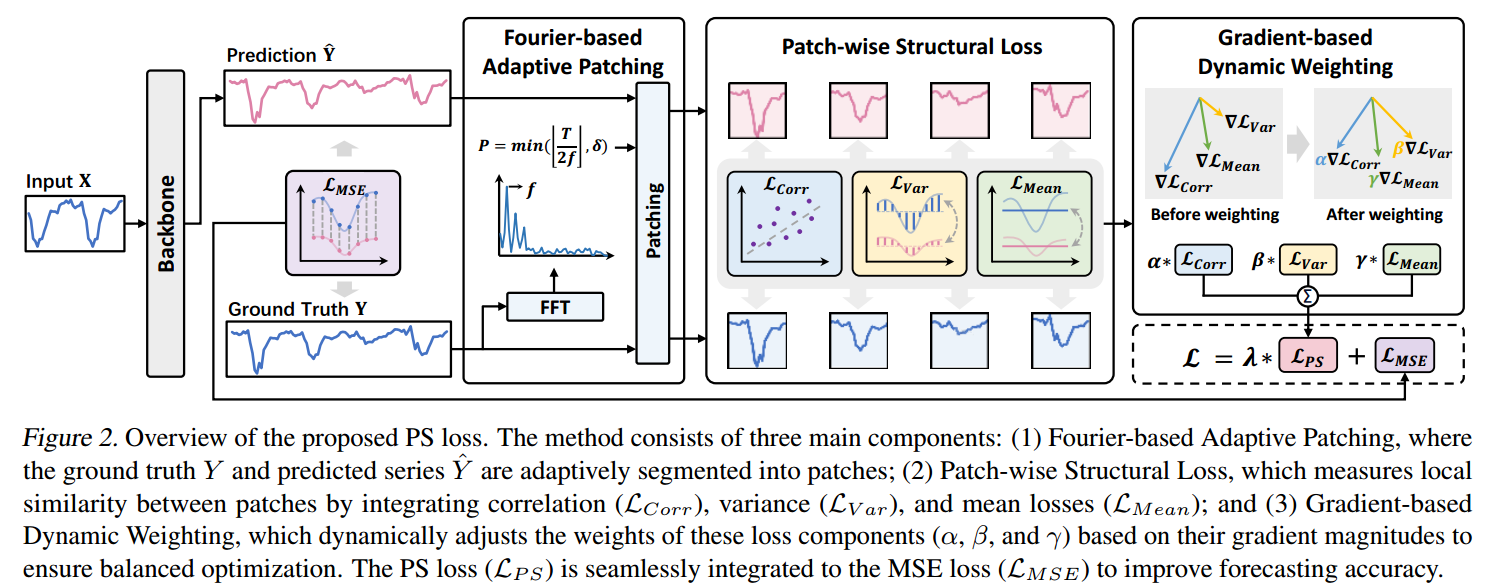
Fourier-based Adaptive Patching
FAP 的主要目标是自适应地确定 一个最能捕获时间序列内在结构模式 和重复周期 的块长度 P。
确定主导周期性
FAP 利用**快速傅里叶变换(FFT)对 真实值序列 **进行分析:
-
计算振幅谱: 首先计算
的 FFT,并提取其振幅值
。振幅谱反映了序列中不同频率分量的强度。
-
识别主导频率: 找到在
中具有最大振幅对应的频率
。这个频率
就是序列的主导频率(dominant frequency),它代表了序列中最显著的重复周期。
-
计算初始周期: 根据主导频率
计算序列的主导周期
,作为初始块长度的候选值。
这个周期
确保了块能够反映序列中反复出现的结构模式。
平衡粒度与一致性
虽然主导周期 提供了结构信息,但它可能导致块过大 ,从而错失更精细的结构细微差别 。为了平衡粒度(granularity)和结构一致性(coherence) ,最终的块长度
进行了调整:
最终块长度 的确定: 最终的块长度
被定义为
系列中的最小值,但同时不能小于一个预设的阈值
。
(注: 论文中的公式 (3) 简化了表示,暗示了一个过程: ,其中
会递增直到达到满足条件的
。这是一个确保
是
的一个较小因子且不低于
的机制。)
-
: 确保
与主导周期
保持关联,但通过除以
减小其尺寸,以捕获更精细的局部结构。
-
: 预设的最小阈值,防止
过小。
分块操作
一旦确定了块长度 ,序列就会被分割成块:
-
步长(Stride): 论文使用步长
,即块长度的一半 ,这意味着相邻的块之间会有重叠。重叠有助于在块边缘实现更平滑的结构化比较。
-
分块结果: 真实序列
和预测序列
都被分割成一组块
和
。
-
块总数: 块的总数量
由序列长度
、块长度
和步长
决定:
。
-
块定义: 第
个块
包含
个连续的时间步,用于后续的结构化损失计算。
总结: FAP 通过傅里叶分析 找到了序列的核心周期性,并基于此周期性自适应地确定 了一个合适的、具有结构意义的块长度 ,为接下来的PS Loss计算奠定了基础。
Patch-wise Structural Loss
PS Loss 通过关注每个 "块" (Patch)内的局部统计特性,旨在捕获和对齐 真实值与预测值之间的结构差异。它由三个互补的损失项构成。
相关性损失 ( )
)
-
目的: 量化真实块和预测块之间方向性(Directionality)和模式(Pattern)的一致性。
-
计算方法: 基于皮尔逊相关系数(Pearson Correlation Coefficient, PCC)
。当两个块的走势(如上升或下降趋势)越一致时,PCC 越接近 1,损失越小。
-
公式:
-
作用: 鼓励模型对齐预测和真实值的趋势和底层模式关系,这对于需要捕捉结构关系而非仅仅点对点准确性的时间序列预测至关重要。
方差损失 ( )
)
-
目的: 确保预测值能代表真实值块内的局部波动(Fluctuation)和变化性(Variability)。
-
核心思想: 不直接比较方差的绝对值,而是软对齐 每个时间步在块内的相对离散程度(Relative Dispersion)。
-
计算方法:
-
计算每个块相对于其均值的偏差 (
和
)。
-
使用 Softmax 函数
将这些偏差值归一化为概率分布。这个分布代表了块内各点相对于均值的相对大小(离散程度)。
-
使用 Kullback--Leibler (KL) 散度来衡量这两个概率分布之间的相似性。
-
-
简化后的公式(利用 Softmax 的平移不变性):
-
作用: 通过对齐块内的相对离散度,该损失鼓励模型捕捉时间序列的底层波动模式,从而生成更具结构连贯性的预测。
均值损失 ( )
)
-
目的: 测量预测块和真实块之间中心趋势(Central Tendency)的一致性 ,以校正系统性偏差(Systematic Shifts or Biases)。
-
计算方法: 定义为真实块均值
和预测块均值
之间的平均绝对误差(Mean Absolute Error, MAE)。
-
公式:
-
作用: 通过对齐平均值,确保预测模型能够维持准确的整体水平 ,并适应时间序列中的动态水平漂移。
PS Loss 的集成
最终的分块结构化损失 () 是这三个独立损失项的加权和:
其中, 是用于平衡 三种损失对整体优化的贡献度的超参数。这种集成方法利用了每个损失项的互补优势,提供了全面的结构对齐。
Gradient-based Dynamic Weighting
GDW 的核心目标是动态平衡 损失中的三个结构分量 (
) 的贡献。这是必要的,因为它们可能具有不同的量级(scales),导致模型过度优化其中一个而忽略其他。
动态权重计算
GDW 使用每个损失项关于模型输出层参数 的梯度范数(
-norm of the gradient)来衡量该损失项对优化过程的影响程度:
-
计算梯度范数:
-
计算平均梯度范数:
-
计算动态权重: 权重被设置为平均梯度范数与该项自身梯度范数之比。这个比值的作用是:如果某个损失项的梯度范数较大(说明它对优化的影响较大,或者其优化得还不够),它的动态权重就会减小(被惩罚),反之亦然。这迫使所有损失项的梯度保持在一个相似的水平,以实现平衡优化。
均值损失的权重精炼
对于均值损失 的权重
,引入了额外的两个缩放因子
和
进行调整:
-
缩放因子 c 和 v:
其中,
是真实值和预测值之间的协方差,
和
是它们的标准差。
-
作用: c 和 v 都在
范围内,并且随着预测值在相关性和方差 方面与真实值对齐得越好 而增大。这意味着:
-
只有当模型已经很好地捕捉到序列的结构(相关性)和波动(方差)时,
的相对权重才会增加。
-
这确保了
主要在优化后期 或结构对齐良好时 发挥作用,用于精细校正预测偏差(即均值)。
-
最终的总损失函数
最后,将标准均方误差(MSE)损失 和集成了动态权重的分块结构化损失(PS Loss)
结合起来,形成最终用于模型优化的总损失函数:
-
: 传统的点对点损失,处理全局点对点误差。
-
: 结构化损失,处理局部结构差异。
-
: 一个超参数,用于控制 PS Loss 在总损失中的贡献度。
实验
实验设置
数据集 (Datasets)
论文使用了七个真实世界的多变量时间序列数据集来验证其方法的泛化能力和有效性:
-
ETT : ETTh1, ETTh2, ETTm1, ETTm2
-
Weather
-
ECL
-
Exchange
骨干模型 (Backbones)
为了全面评估 PS Loss 的效果,论文选择了五种 具有多样化架构的最新(SOTA)时间序列预测模型作为骨干(即 PS Loss 将集成到这些模型的训练中):
| 模型类型 | 模型名称 | 特点 |
| 基于 Transformer | iTransformer | 可能侧重于逆向注意力或特定的 Transformer 变体。 |
| 基于 Transformer | PatchTST | 使用 **分块(Patching)**方法将长序列分解为短块,以捕获局部语义。 |
| 基于 MLP | DLinear | 线性模型,通过分解和简单 MLP 实现 SOTA 性能。 |
| 基于 MLP | TimeMixer | 使用 MLP 结构进行特征混合和时间混合。 |
| 基于 CNN | TimesNet | 基于时空分析 和多尺度分解的卷积网络。 |
|---|
实现细节
为了保证公平评估,论文在集成 PS Loss 时采用了严格的控制变量方法:
-
基线一致性: 骨干模型使用了官方实现 ,并沿用了它们原始的实验和超参数设置。
-
仅调整 PS Loss 相关参数: 只有两个超参数被调整:
-
PS Loss 权重
: 控制
在总损失
中的贡献度。
-
分块长度阈值
: FAP 方法中用于限制最小块长度的参数。
-
-
计算资源: 实验是在 PyTorch 框架上,使用 NVIDIA RTX 3090 24GB GPU 执行的。
Main Results
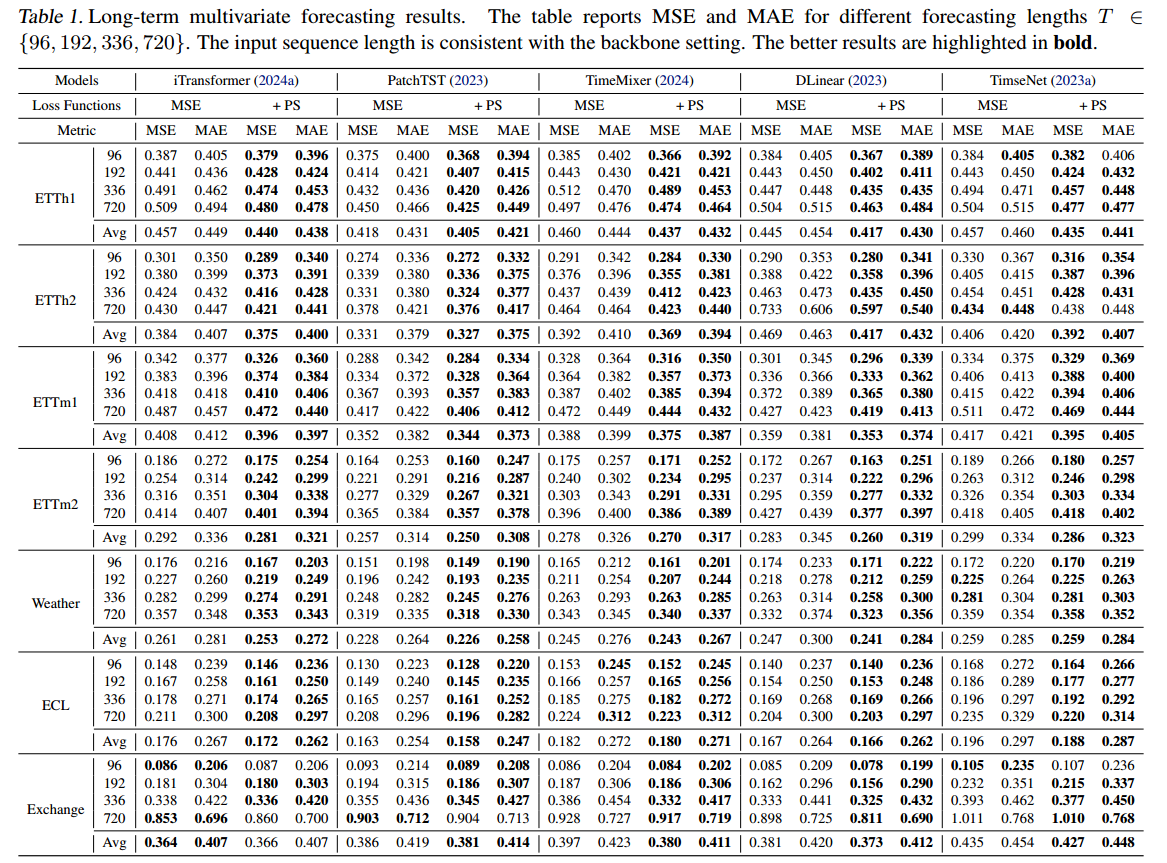
在 DLinear 模型上取得了显著的进步,MSE 平均降低 5.22%,MAE 平均降低 4.39%;
在 140 个测试案例中,有 134 个 PS Loss 的性能优于标准的 MSE Loss。
Results on LLM-based Models
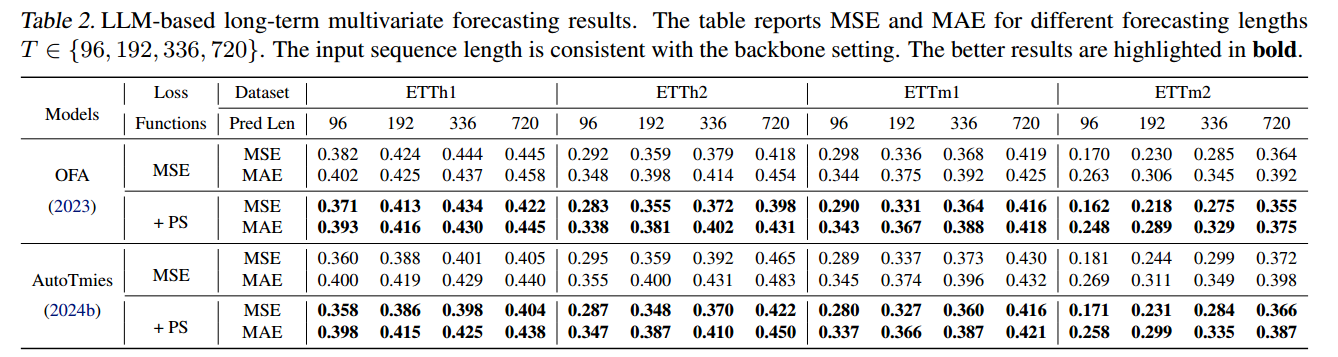
集成 PS Loss 后,性能一致地优于标准的 MSE Loss。
Comparison with Other Loss Functions
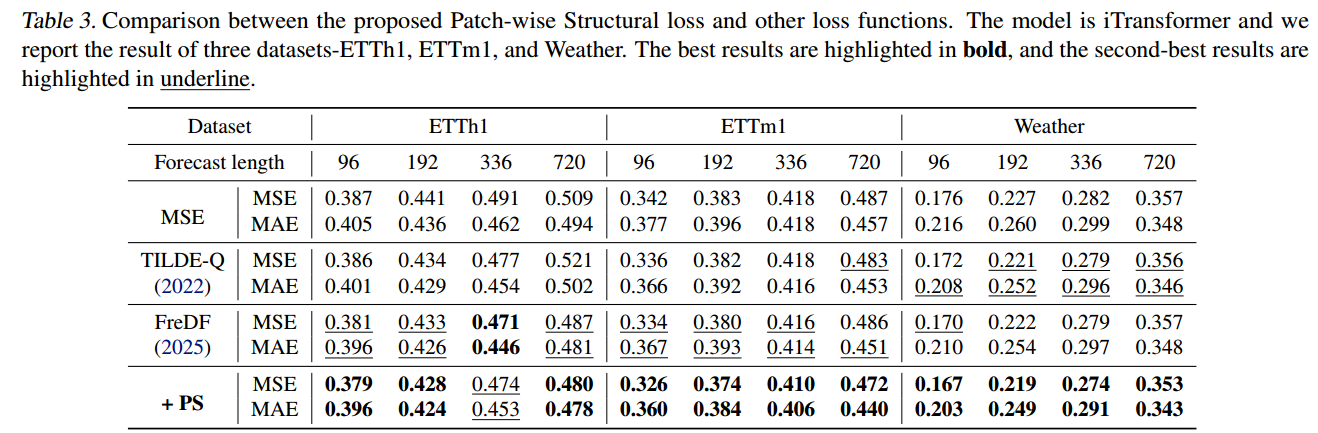
-
在大多数数据集和预测范围下,PS Loss 实现了最低的 MSE 和 MAE。
-
这归功于 PS Loss 能够通过在块级别 评估相关性、方差和均值 ,有效地测量局部结构相似性,实现更精确的对齐。
Ablation Study
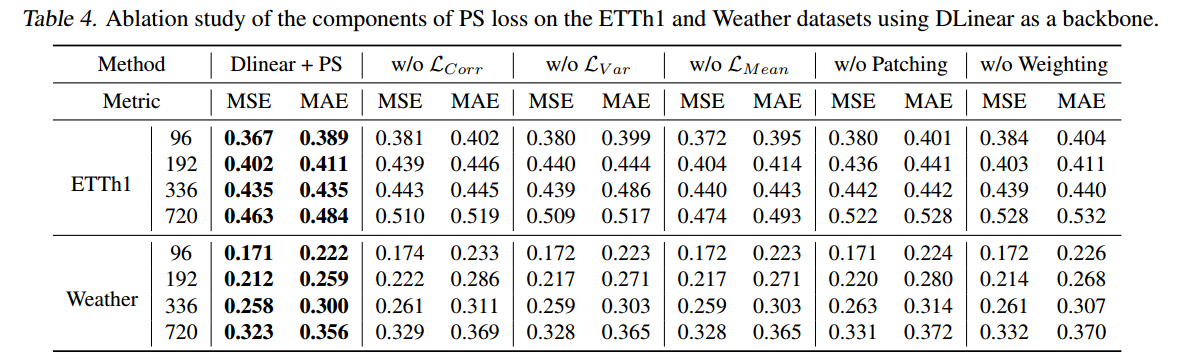
使用 DLinear 模型在 ETTh1 和 Weather 数据集上进行消融实验,评估 各个组件的贡献:
-
损失分量: 移除
中的任何一个分量,都会导致性能明显下降 ,强调了这些分量在捕获局部结构相似性方面的协同关系(synergistic relationship)。
-
自适应分块(Adaptive Patching): 如果不进行分块而直接处理整个时间序列,性能会显著恶化 ,尤其是在长预测范围内,证明了分块机制在捕获细粒度模式中的价值。
-
动态加权(Dynamic Weighting, GDW): 用固定的权重(1.0)替代动态加权会导致性能下降 ,证明了动态加权能够有效地平衡 各个损失项,从而改善优化和预测效果。
Zero-shot Forecasting
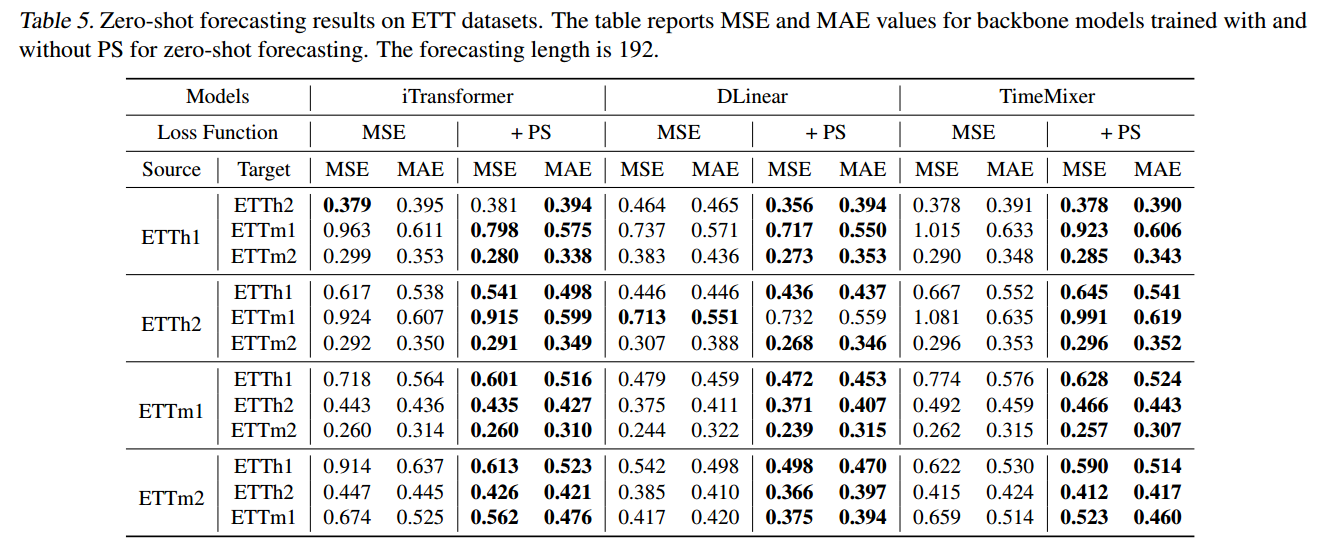
- 在 36 个场景中,PS Loss 优于 MSE Loss 34 次 ,表明它在跨数据集和粒度方面带来了实质性的泛化能力提升。
Forecasting Visualization
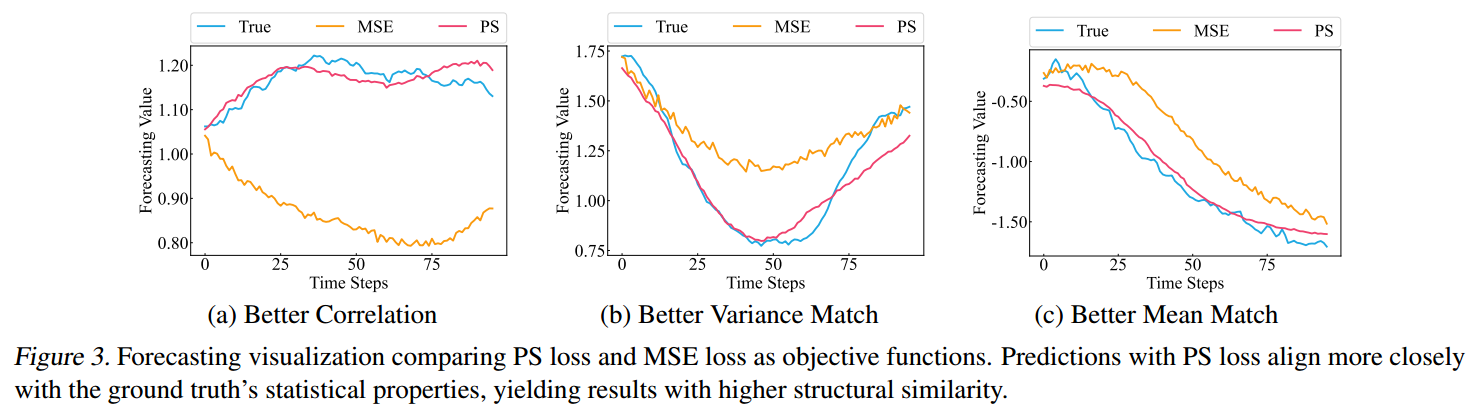
观察结果: 使用 iTransformer 在 Weather 数据集上进行的可视化(如图 3)显示,与 MSE Loss 相比,PS Loss 显著改善了与真实值的对齐:
-
预测紧密跟随 真实值的轨迹,保留了整体趋势和模式。
-
有效地捕获了振幅波动 ,反映了局部变化性。
-
减少了整体水平上的偏差,确保了与中心趋势的更好对齐。
Hyperparameter Sensitivity
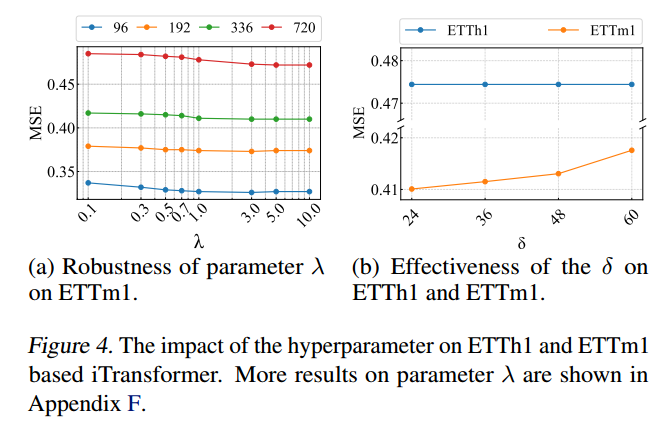
PS损失权重λ
权重 λ 决定PS损失与MSE的相对重要性,性能随着λ的增加而提高,在λ = 3.0时达到峰值。
性能在 λ 的宽范围内保持稳定,表明PS损失是稳健的,可以很容易地应用于各种数据集和模型。
补丁长度阈值δ
补丁长度阈值 δ 限制最大补丁长度以保持比较的粒度。
对于ETTh 1,基于傅立叶的补丁长度小于δ,增加δ不会影响性能。
对于ETTm 1,其中基于傅立叶的补丁长度超过δ,较大的δ导致性能降低,表明过大的补丁模糊了细粒度的结构模式,并且适当的补丁长度对于结构对齐至关重要。