HOT100-图论类型题

HOT100系列-图论类题目

核心思想

例题

1、岛屿数量

题目描述：

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

**输入：**grid = [

'1','1','1','1','0'\], \['1','1','0','1','0'\], \['1','1','0','0','0'\], \['0','0','0','0','0'

]

**输出：**1

示例 2：

**输入：**grid = [

'1','1','0','0','0'\], \['1','1','0','0','0'\], \['0','0','1','0','0'\], \['0','0','0','1','1'

]

**输出：**3

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 300
• grid[i][j] 的值为 '0' 或 '1'

解题思路：

• 洪水填充法

代码如下：

class Solution {

    public int numIslands(char[][] grid) {

        int m=grid.length;

        int n=grid[0].length;

        int ans=0;

        for(int i=0;i<m;i++){

            for(int j=0;j<n;j++){

                if(grid[i][j]=='1'){

                    ans++;

                    dfs(grid,i,j);

                }

            }

        }

        return ans;

    }

  

    public void dfs(char[][] grid,int i,int j){

        //越界,或者对应位格数字不为1

        if(i<0 || i==grid.length || j<0 || j==grid[0].length || grid[i][j]!='1'){

            return;

        }

        //将当前点置为0

        grid[i][j]='0';

        //上下左右填充遍历

        dfs(grid,i-1,j);

        dfs(grid,i+1,j);

        dfs(grid,i,j-1);

        dfs(grid,i,j+1);

    }

}

2、腐烂的橘子

题目描述：

在给定的 m x n 网格 grid 中，每个单元格可以有以下三个值之一：

• 值 0 代表空单元格；
• 值 1 代表新鲜橘子；
• 值 2 代表腐烂的橘子。

每分钟，腐烂的橘子 周围 4 个方向上相邻 的新鲜橘子都会腐烂。

返回 直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

示例 1：

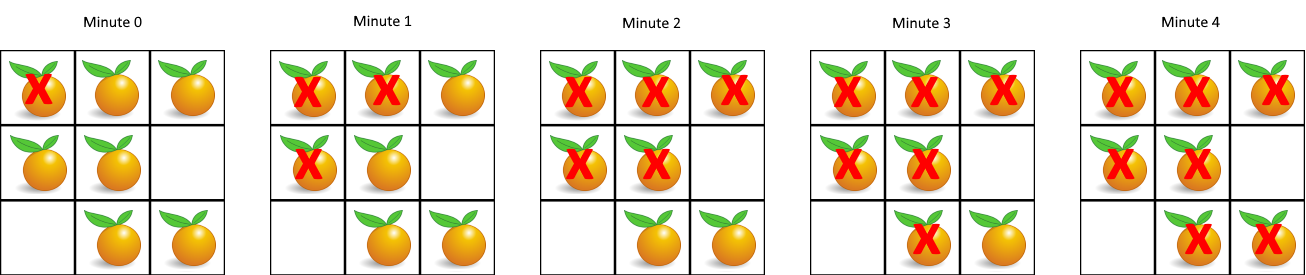
**输入：**grid = [[2,1,1],[1,1,0],[0,1,1]]

**输出：**4

示例 2：

**输入：**grid = [[2,1,1],[0,1,1],[1,0,1]]
输出： -1

**解释：**左下角的橘子（第 2 行， 第 0 列）永远不会腐烂，因为腐烂只会发生在 4 个方向上。

示例 3：

**输入：**grid = [[0,2]]

**输出：**0

**解释：**因为 0 分钟时已经没有新鲜橘子了，所以答案就是 0 。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 10
• grid[i][j] 仅为 0、1 或 2

解题思路：

• 多源dfs
• 本题与上题不同的就在于，本题要的是感染轮数，上一种dfs写法不顾及轮数，直接能一直感染就一直感染
• 先统计好橘子的数量以及坏橘子的位置坐标
• 每一轮的感染中用坏橘子从4个方向去感染好橘子，然后统计本轮感染的好橘子位置，下一轮用新收集的接着感染

代码如下：

class Solution {

    //四个方向

    public static int[][]directions={{-1,0},{1,0},{0,-1},{0,1}};

    public static int orangesRotting(int[][] grid) {

        int m=grid.length;

        int n=grid[0].length;

        //统计初始时新鲜橘子数量和腐烂橘子的位置

        int fresh=0;

        List<int[]> q=new ArrayList<>();

        for(int i=0;i<m;i++){

            for(int j=0;j<n;j++){

                if(grid[i][j]==1){

                    fresh++;

                }

                if(grid[i][j]==2){

                    q.add(new int[]{i,j});

                }

            }

        }

        int ans=0;

        //开始多源dfs，每轮都将现在腐烂橘子周围的好橘子腐化

        while(!q.isEmpty() && fresh>0){

            List<int[]>temp=q;

            //收集这一轮新增的坏橘子

            q=new ArrayList<>();

            ans++;

            //遍历这一轮的每一个坏橘子，将其周围的好橘子感染

            for(int[] pos:temp){

                for(int[]d:directions){

                    int i=pos[0]+d[0];

                    int j=pos[1]+d[1];

                    //将本轮感染的好橘子加入下一轮的坏橘子中

                    if(i>=0 && i<m && j>=0 && j<n && grid[i][j]==1){

                        fresh--;

                        grid[i][j]=2;

                        q.add(new int[]{i,j});

                    }

                }

            }

        }

        return fresh>0?-1:ans;

    }

}

3、课程表

题目描述：

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

• 例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。

请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

示例 1：

**输入：**numCourses = 2, prerequisites = [[1,0]]

**输出：**true

**解释：**总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。

示例 2：

**输入：**numCourses = 2, prerequisites = [[1,0],[0,1]]

**输出：**false

**解释：**总共有 2 门课程。学习课程 1 之前，你需要先完成​课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

提示：

• 1 <= numCourses <= 2000
• 0 <= prerequisites.length <= 5000
• prerequisites[i].length == 2
• 0 <= ai, bi < numCourses
• prerequisites[i] 中的所有课程对 互不相同

解题思路：

• 拓扑排序

代码如下

class Solution {

    public static int MAXN=2001;

    public static int MAXM=5001;

    //链式前向星

    public static int[]head=new int[MAXN];

    public static int[]next=new int[MAXM];

    public static int[]to=new int[MAXM];

    public static int cnt;

    //收集入度为0的队列

    public static int[]queue=new int[MAXN];

    public static int l,r;

    //收集各个节点入度情况

    public static int[]indegree=new int[MAXN];

    //统计给出数据的点，边数

    public static int n,m;

    public static boolean canFinish(int numCourses, int[][] prerequisites) {

        n=numCourses;

        m=prerequisites.length;

        build();

        //开始建图,收集节点的入度

        for(int i=0,u,v;i<m;i++){

            u=prerequisites[i][1];

            v=prerequisites[i][0];

            addEdge(u,v);

            indegree[v]++;

        }

        //队列存储入度为0的点

        l=r=0;

        for(int i=0;i<n;i++){

            if(indegree[i]==0){

                queue[r++]=i;

            }

        }

        //开始拓扑排序

        topSort();

        return r==n;

  

    }

    public static void build(){

        Arrays.fill(head,0,n+1,0);

        cnt=1;

        Arrays.fill(indegree,0,n+1,0);

    }

    public static void addEdge(int u,int v){

        next[cnt]=head[u];

        to[cnt]=v;

        head[u]=cnt++;

    }

  

    public static void topSort(){

        while(l<r){

            int u=queue[l++];

            //遍历u的边

            for(int ei=head[u],v;ei>0;ei=next[ei]){

                v=to[ei];

                if(--indegree[v]==0){

                    queue[r++]=v;

                }

            }

        }

    }

}

4、实现Trie（前缀树）

题目描述：
Trie （发音类似 "try"）或者说 前缀树 是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补全和拼写检查。

请你实现 Trie 类：

• Trie() 初始化前缀树对象。
• void insert(String word) 向前缀树中插入字符串 word 。
• boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
• boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入

"Trie", "insert", "search", "search", "startsWith", "insert", "search"

\[\], \["apple"\], \["apple"\], \["app"\], \["app"\], \["app"\], \["app"\]

输出

null, null, true, false, true, null, true

解释

Trie trie = new Trie();

trie.insert("apple");

trie.search("apple"); // 返回 True

trie.search("app"); // 返回 False

trie.startsWith("app"); // 返回 True

trie.insert("app");

trie.search("app"); // 返回 True

提示：

• 1 <= word.length, prefix.length <= 2000
• word 和 prefix 仅由小写英文字母组成
• insert、search 和 startsWith 调用次数 总计 不超过 3 * 104 次
  解题思路：
• 题目都说了这是一个前缀树，但是由于小写字母任意都开头，所以我们在构建的时候，每个节点都有26个分叉，即26叉树
• 同时为了判别某个字符串是否加入其中，我们需要再每个节点加入boolean变量来确定它是否为某个字符的最后一个节点

代码如下：

class Trie {

    private static class Node{

        //构建26叉树

        Node[] son=new Node[26];

        //表示这个节点是不是尾节点，用来看某个字符是否在加入过

        boolean end=false;

    }

    //统一根节点

    public Node root;

  

    public Trie() {

        root=new Node();

    }

    public void insert(String word) {

        Node cur=root;

        for(char c:word.toCharArray()){

            c-='a';

            if(cur.son[c]==null){

                cur.son[c]=new Node();

            }

            cur=cur.son[c];

        }

        cur.end=true;

    }

    public boolean search(String word) {

        return find(word)==2;

    }

    public boolean startsWith(String prefix) {

        return find(prefix)!=0;

    }

  

    public int find(String word){

        Node cur=root;

        for(char c:word.toCharArray()){

            c-='a';

            if(cur.son[c]==null){

                return 0;

            }

            cur=cur.son[c];

        }

        //若最后这个节点是尾节点，则说明有一个字符串加入，否则，则说明是某些字符串的前缀

        return cur.end?2:1;

    }

}