深度学习实战（基于pytroch）系列（三十三）循环神经网络RNN

循环神经网络RNN

• • 不含隐藏状态的神经网络
  • 含隐藏状态的循环神经网络
  • • 核心组件
    • 信息流动过程
    • 关键特征
    • [对输出 O t − 1 O_{t-1} Ot−1, O t O_t Ot, O t + 1 O_{t+1} Ot+1的理解](#对输出 O t − 1 O_{t-1} Ot−1, O t O_t Ot, O t + 1 O_{t+1} Ot+1的理解)
    • • 数据准备
      • 时间步1：输入"我"
      • 时间步2：输入"爱"
      • 时间步3：输入"学习"
  • PyTorch实现
  • 小结

上一节介绍的 n n n 元语法模型中，时间步 t t t 的词 w t w_t wt 基于前面所有词的条件概率只考虑了最近时间步的 n − 1 n-1 n−1 个词。如果要考虑比 t − ( n − 1 ) t-(n-1) t−(n−1) 更早时间步的词对 w t w_t wt 的可能影响，我们需要增大 n n n。但这样模型参数的数量将随之呈指数级增长。

本节将介绍循环神经网络。它并非刚性地记忆所有固定长度的序列，而是通过隐藏状态来存储之前时间步的信息。首先我们回忆一下前面介绍过的多层感知机，然后描述如何添加隐藏状态来将它变成循环神经网络。

不含隐藏状态的神经网络

让我们考虑一个含单隐藏层的多层感知机。给定样本数为 n n n、输入个数（特征数或特征向量维度）为 d d d 的小批量数据样本 X ∈ R n × d \boldsymbol{X} \in \mathbb{R}^{n \times d} X∈Rn×d。设隐藏层的激活函数为 ϕ \phi ϕ，那么隐藏层的输出 H ∈ R n × h \boldsymbol{H} \in \mathbb{R}^{n \times h} H∈Rn×h 计算为

H = ϕ ( X W x h + b h ) , \boldsymbol{H} = \phi(\boldsymbol{X} \boldsymbol{W}_{xh} + \boldsymbol{b}_h), H=ϕ(XWxh+bh),

其中隐藏层权重参数 W x h ∈ R d × h \boldsymbol{W}_{xh} \in \mathbb{R}^{d \times h} Wxh∈Rd×h，隐藏层偏差参数 b h ∈ R 1 × h \boldsymbol{b}_h \in \mathbb{R}^{1 \times h} bh∈R1×h， h h h 为隐藏单元个数。把隐藏变量 H \boldsymbol{H} H 作为输出层的输入，且设输出个数为 q q q（如分类问题中的类别数），输出层的输出为

O = H W h q + b q , \boldsymbol{O} = \boldsymbol{H} \boldsymbol{W}_{hq} + \boldsymbol{b}_q, O=HWhq+bq,

其中输出变量 O ∈ R n × q \boldsymbol{O} \in \mathbb{R}^{n \times q} O∈Rn×q，输出层权重参数 W h q ∈ R h × q \boldsymbol{W}_{hq} \in \mathbb{R}^{h \times q} Whq∈Rh×q，输出层偏差参数 b q ∈ R 1 × q \boldsymbol{b}_q \in \mathbb{R}^{1 \times q} bq∈R1×q。如果是分类问题，我们可以使用 softmax ( O ) \text{softmax}(\boldsymbol{O}) softmax(O) 来计算输出类别的概率分布。

含隐藏状态的循环神经网络

现在我们考虑输入数据存在时间相关性的情况。假设 X t ∈ R n × d \boldsymbol{X}t \in \mathbb{R}^{n \times d} Xt∈Rn×d 是序列中时间步 t t t 的小批量输入， H t ∈ R n × h \boldsymbol{H}t \in \mathbb{R}^{n \times h} Ht∈Rn×h 是该时间步的隐藏变量。与多层感知机不同的是，这里我们保存上一时间步的隐藏变量 H t − 1 \boldsymbol{H}{t-1} Ht−1，并引入一个新的权重参数 W h h ∈ R h × h \boldsymbol{W}{hh} \in \mathbb{R}^{h \times h} Whh∈Rh×h，该参数用来描述在当前时间步如何使用上一时间步的隐藏变量。具体来说，时间步 t t t 的隐藏变量的计算由当前时间步的输入和上一时间步的隐藏变量共同决定：

H t = ϕ ( X t W x h + H t − 1 W h h + b h ) . \boldsymbol{H}t = \phi(\boldsymbol{X}t \boldsymbol{W}{xh} + \boldsymbol{H}{t-1} \boldsymbol{W}_{hh} + \boldsymbol{b}_h). Ht=ϕ(XtWxh+Ht−1Whh+bh).

与多层感知机相比，我们在这里添加了 H t − 1 W h h \boldsymbol{H}{t-1} \boldsymbol{W}{hh} Ht−1Whh 一项。由上式中相邻时间步的隐藏变量 H t \boldsymbol{H}t Ht 和 H t − 1 \boldsymbol{H}{t-1} Ht−1 之间的关系可知，这里的隐藏变量能够捕捉截至当前时间步的序列的历史信息，就像是神经网络当前时间步的状态或记忆一样。因此，该隐藏变量也称为隐藏状态。由于隐藏状态在当前时间步的定义使用了上一时间步的隐藏状态，上式的计算是循环的。使用循环计算的网络即循环神经网络（recurrent neural network）。

循环神经网络有很多种不同的构造方法。含上式所定义的隐藏状态的循环神经网络是极为常见的一种。在时间步 t t t，输出层的输出和多层感知机中的计算类似：

O t = H t W h q + b q . \boldsymbol{O}_t = \boldsymbol{H}t \boldsymbol{W}{hq} + \boldsymbol{b}_q. Ot=HtWhq+bq.

循环神经网络的参数包括隐藏层的权重 W x h ∈ R d × h \boldsymbol{W}{xh} \in \mathbb{R}^{d \times h} Wxh∈Rd×h、 W h h ∈ R h × h \boldsymbol{W}{hh} \in \mathbb{R}^{h \times h} Whh∈Rh×h 和偏差 b h ∈ R 1 × h \boldsymbol{b}h \in \mathbb{R}^{1 \times h} bh∈R1×h，以及输出层的权重 W h q ∈ R h × q \boldsymbol{W}{hq} \in \mathbb{R}^{h \times q} Whq∈Rh×q 和偏差 b q ∈ R 1 × q \boldsymbol{b}_q \in \mathbb{R}^{1 \times q} bq∈R1×q。值得一提的是，即便在不同时间步，循环神经网络也始终使用这些模型参数。因此，循环神经网络模型参数的数量不随时间步的增加而增长。

下图展示的是循环神经网络（RNN）在三个连续时间步（t-1, t, t+1）的计算过程。

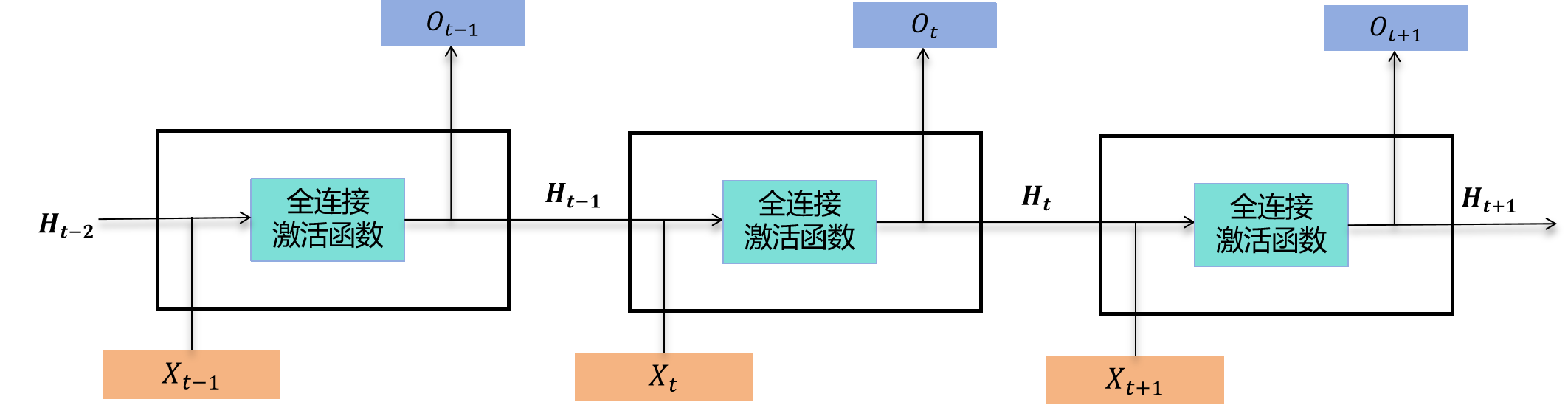
核心组件

• 输入层 ： X t − 1 X_{t-1} Xt−1, X t X_t Xt, X t + 1 X_{t+1} Xt+1 分别表示不同时间步的输入数据
• 隐藏状态 ： H t − 1 H_{t-1} Ht−1, H t H_t Ht 表示随时间传递的隐藏状态（记忆）
• 输出层：每个时间步都会产生相应的输出
• 全连接层和激活函数 ϕ \phi ϕ：核心计算单元

信息流动过程

时间步 t 的计算流程：

1. 输入合并 ：将当前输入 X t X_t Xt 和前一时刻的隐藏状态 H t − 1 H_{t-1} Ht−1 **连结（concatenate）**在一起
2. 全连接变换 ：连结后的数据通过全连接层和激活函数 ϕ \phi ϕ 进行处理
3. 生成新状态 ：计算得到当前时间步的隐藏状态 H t H_t Ht
4. 输出生成 ：基于 H t H_t Ht 生成当前时间步的输出

关键特征

1. 时间依赖性：

   • H t H_t Ht 的计算依赖于 X t X_t Xt 和 H t − 1 H_{t-1} Ht−1
   • 信息通过隐藏状态在时间维度上传递

2. 参数共享：

   • 所有时间步使用相同的全连接层参数（权重矩阵）
   • 体现了"循环"的核心思想

3. 记忆机制：

   • 隐藏状态 H H H 充当网络的"记忆"
   • 能够捕捉序列中的长期依赖关系

对输出 O t − 1 O_{t-1} Ot−1, O t O_t Ot, O t + 1 O_{t+1} Ot+1的理解

假设我们有一个句子："我 爱 学习"，我们要预测每个词的下一个词。

数据准备

• 词汇表：{"我", "爱", "学习", "编程"}
• 输入序列："我" → "爱" → "学习"
• 目标：预测下一个词的概率分布

时间步1：输入"我"

输入: X₁ = "我" (词向量)
隐藏状态: H₁ = ϕ("我"的向量 + 初始状态)
输出: O₁ = softmax(H₁ × W_hq + b_q)

O₁的具体内容：

[0.15, 0.60, 0.20, 0.05]  # 4个词的概率分布
对应： ["我", "爱", "学习", "编程"]
解释：基于"我"预测下一个词，"爱"的概率最高(0.60)

时间步2：输入"爱"

输入: X₂ = "爱" (词向量) + 隐藏状态H₁
隐藏状态: H₂ = ϕ("爱"的向量 + H₁)  # 包含了"我"的信息
输出: O₂ = softmax(H₂ × W_hq + b_q)

O₂的具体内容：

[0.05, 0.10, 0.75, 0.10]  # 4个词的概率分布
对应： ["我", "爱", "学习", "编程"]
解释：基于"我爱"预测下一个词，"学习"的概率最高(0.75)

时间步3：输入"学习"

输入: X₃ = "学习" (词向量) + 隐藏状态H₂
隐藏状态: H₃ = ϕ("学习"的向量 + H₂)  # 包含了"我爱"的信息
输出: O₃ = softmax(H₃ × W_hq + b_q)

O₃的具体内容：

[0.10, 0.05, 0.15, 0.70]  # 4个词的概率分布
对应： ["我", "爱", "学习", "编程"]
解释：基于"我爱学习"预测下一个词，"编程"的概率最高(0.70)

PyTorch实现

我们刚刚提到，隐藏状态中 X t W x h + H t − 1 W h h \boldsymbol{X}t \boldsymbol{W}{xh} + \boldsymbol{H}{t-1} \boldsymbol{W}{hh} XtWxh+Ht−1Whh 的计算等价于 X t \boldsymbol{X}t Xt 与 H t − 1 \boldsymbol{H}{t-1} Ht−1 连结后的矩阵乘以 W x h \boldsymbol{W}{xh} Wxh 与 W h h \boldsymbol{W}{hh} Whh 连结后的矩阵。接下来，我们用一个具体的例子来验证这一点。

首先，我们构造矩阵X、W_xh、H和W_hh，它们的形状分别为(3, 1)、(1, 4)、(3, 4)和(4, 4)。将X与W_xh、H与W_hh分别相乘，再把两个乘法运算的结果相加，得到形状为(3, 4)的矩阵。

import torch

X, W_xh = torch.randn(3, 1), torch.randn(1, 4)
H, W_hh = torch.randn(3, 4), torch.randn(4, 4)
torch.matmul(X, W_xh) + torch.matmul(H, W_hh)

输出

tensor([[-0.2345, 1.5432, 0.7891, -1.2345],

0.4567, -0.8912, 1.2345, 0.5678\], \[-1.2345, 0.6789, -0.4567, 1.8912\]\])

将矩阵X和H按列（维度1）连结，连结后的矩阵形状为(3, 5)。可见，连结后矩阵在维度1的长度为矩阵X和H在维度1的长度之和（ 1 + 4 1+4 1+4）。然后，将矩阵W_xh和W_hh按行（维度0）连结，连结后的矩阵形状为(5, 4)。最后将两个连结后的矩阵相乘，得到与上面代码输出相同的形状为(3, 4)的矩阵。

torch.matmul(torch.cat((X, H), dim=1), torch.cat((W_xh, W_hh), dim=0))

输出

tensor([[-0.2345, 1.5432, 0.7891, -1.2345],

0.4567, -0.8912, 1.2345, 0.5678\], \[-1.2345, 0.6789, -0.4567, 1.8912\]\])

小结

• 使用循环计算的网络即循环神经网络。
• 循环神经网络的隐藏状态可以捕捉截至当前时间步的序列的历史信息。
• 循环神经网络模型参数的数量不随时间步的增加而增长。
• 可以基于字符级循环神经网络来创建语言模型。