一、队列:数据结构中的 "排队艺术"
在编程世界里,队列(Queue)是一种遵循 "先进先出"(FIFO,First In First Out)规则的线性数据结构,就像我们日常生活中的排队场景 ------ 先到的人先服务,后到的人只能依次排队等候。这种特性让队列在众多场景中发挥着不可替代的作用:
- 任务调度:操作系统中的进程调度、打印机任务队列,都是通过队列实现任务的有序执行;
- 数据缓冲:网络通信中,数据包的接收和发送常采用队列作为缓冲,避免数据丢失或拥堵;
- 广度优先搜索(BFS):图论算法中,BFS 遍历必须依赖队列存储待访问的节点,确保遍历顺序的正确性。
作为 C 语言开发者,手动实现队列是掌握数据结构的基础技能,也是提升代码效率的关键。今天我们就从原理到实战,结合完整代码案例,深入探讨队列的 C 语言实现逻辑。
二、队列的核心操作与设计思路
队列的核心操作并不复杂,围绕 "入队""出队""判空""判满""获取队头元素" 这五大功能展开。在 C 语言中,队列的实现主要有两种方式:数组实现(顺序队列) 和链表实现(链式队列)。本文聚焦数组实现(即顺序队列),这也是你提供的代码采用的方式,其优势在于存储紧凑、访问高效,适合固定容量的场景。

- 数据结构定义
首先需要定义队列的结构体,核心包含三个部分:
- 存储数据的数组 data:采用固定大小的数组(maxsize=100),限制队列最大容量;
- 队头指针 front:指向队列第一个元素的位置,出队时移动;
- 队尾指针 rear:指向队列最后一个元素的下一个位置,入队时移动。
代码中的定义如下,逻辑清晰且符合 C 语言规范:
#define maxsize 100
typedef int elemtype;
typedef struct queue{
elemtype data[maxsize]; // 存储队列元素
int front; // 队头指针(出队端)
int rear ; // 队尾指针(入队端)
}queue;
- 核心操作的实现逻辑剖析
(1)初始化队列(initqueue)
初始化的核心是让队头和队尾指针都指向起始位置(索引 0),此时队列为空。这一步是队列使用的前提,避免野指针导致的内存异常:
void initqueue(queue*Q){
Q->front=0;
Q->rear =0;
}

(2)判空操作(is_empty)
判断队列是否为空的标准很简单:当 front == rear 时,说明队列中没有元素。这里需要注意代码的小细节 ------ 函数返回值设计为 elemtype(本质是 int),返回 1 表示空,0 表示非空,同时增加打印提示,提升调试友好性:
elemtype is_empty(queue*Q){
if(Q->front==Q->rear){
printf("是空的");
return 1;
}
else{
return 0;
}
}

(3)入队操作(pushqueue)
入队是将元素添加到队尾,但需先判断队列是否已满(rear >= maxsize)。这里代码的亮点的是:并非直接判满,而是调用 queuefull 函数进行 "数据搬移" 优化------ 当队列前方有出队后留下的空闲空间时,将所有元素向前移动,复用空闲空间,避免 "假溢出"(即数组未满但队尾已达边界)。
优化后的入队逻辑:若队列未满或可通过搬移复用空间,则将元素存入 data[rear],并让 rear 自增:
elemtype pushqueue(queue*Q,elemtype e){
if(Q->rear>=maxsize){
if(queuefull(Q)){ // 尝试搬移空间,若真满则返回0
return 0;
}
}
Q->data[Q->rear]=e;
Q->rear++;
return 1;
}
(4)空间复用逻辑(queuefull)
这是代码中最具巧思的部分,也是解决顺序队列 "假溢出" 的关键。当队尾到达数组边界时,检查队头是否大于 0(即前方有空闲空间):
- 若是,则将从 front 到 rear 的元素整体向前移动 front 个位置,让队头重新指向 0,队尾更新为 rear - front;
- 若否(front=0,无空闲空间),则说明队列真满,返回 1。
这种设计让数组空间得到充分利用,相比 "一次性判满" 的简单实现,实用性更强:
int queuefull(queue*Q){
if(Q->front>0){// 存在空闲空间,进行数据搬移
int tem=Q->front;
for(int i=Q->front;i<=Q->rear;i++){
Q->data[i-tem]=Q->data[i];
}
Q->front=0; // 队头重置为0
Q->rear=Q->rear-tem; // 队尾更新为实际元素个数
return 0;
}
else{
printf("真的满了\n");
return 1;
}
}
(5)出队与获取队头(dequeue & get_queue)
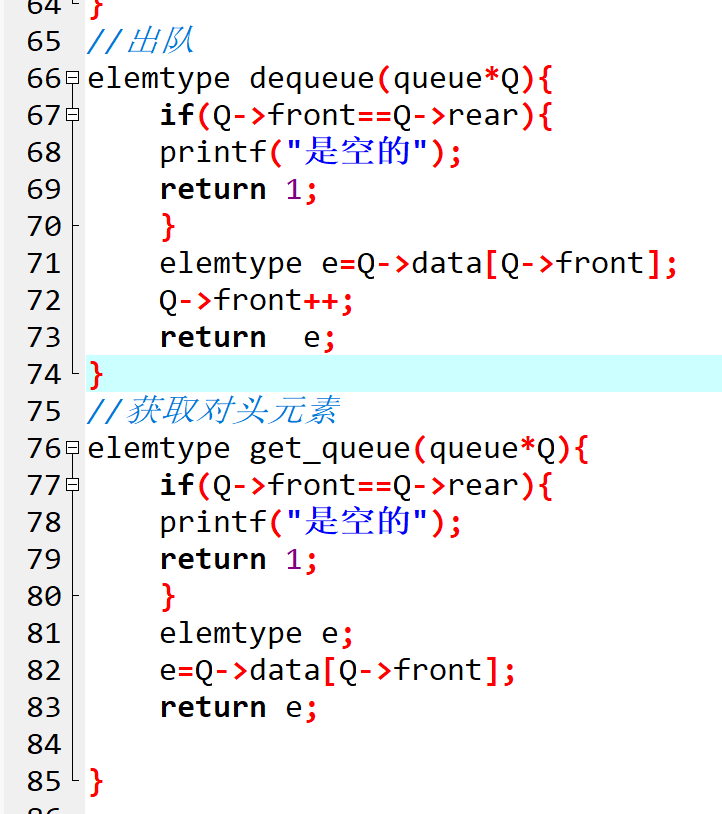
出队是从队头取出元素,需先判空;获取队头元素则仅返回队头值,不改变队列结构。两者逻辑类似,均需先检查 front == rear(空队列),避免访问无效内存:
// 出队:取出队头元素并移动front
elemtype dequeue(queue*Q){
if(Q->front==Q->rear){
printf("是空的");
return 1;
}
elemtype e=Q->data[Q->front];
Q->front++;
return e;
}
// 获取队头元素:仅读取不删除
elemtype get_queue(queue*Q){
if(Q->front==Q->rear){
printf("是空的");
return 1;
}
elemtype e=Q->data[Q->front];
return e;
}
三、实战测试:队列功能验证
代码的 main 函数提供了完整的测试用例,我们可以一步步拆解执行过程,直观感受队列的工作机制:
- 初始化队列 q,front=0,rear=0;
- 四次入队:依次添加 8、88、888、8888,此时 rear=4,front=0,队列元素为 [8,88,888,8888];
- 获取队头元素:返回 8,队列结构不变;
- 两次出队:依次取出 8、88,此时 front=2,rear=4,队列剩余 [888,8888];
- 再次获取队头元素:返回 888。
最终输出结果为:
测试用例覆盖了入队、出队、获取队头的核心场景,验证了代码的正确性。
四、深度思考:代码优化与拓展方向
虽然这份代码实现了队列的基本功能,但在实际开发中仍有优化空间,这也是数据结构学习的核心 ------灵活适配场景:
- 动态扩容:当前队列容量固定为 100,可改为动态数组(通过 malloc/realloc 分配内存),避免容量不足;
- 循环队列优化:数据搬移操作会消耗时间(时间复杂度 O (n)),更高效的方式是实现循环队列 ------ 通过取模运算((rear+1)%maxsize)判断队列满,无需搬移元素,时间复杂度降至 O (1);
- 链式队列实现:对于容量不确定的场景,链式队列(用链表存储)更合适,可动态增减节点,无溢出问题,但需额外维护指针,空间开销略大。
五、互动交流:你的队列实战经验?
队列作为基础数据结构,看似简单,但在实际开发中往往能解决关键问题。比如我曾用循环队列优化过嵌入式系统中的串口数据接收逻辑,避免了数据丢失;还有同学用队列实现了简易的消息队列,解决了多线程通信的同步问题。
那么你呢?在项目中用过队列吗?遇到过哪些坑(比如假溢出、线程安全问题)?或者有更巧妙的队列实现方式?欢迎在评论区分享你的经验和思考,我们一起探讨数据结构的实战技巧!
如果需要完整的循环队列代码、链式队列实现,或者想深入了解队列在多线程中的应用,也可以在评论区留言,后续我会针对性输出相关内容~