2.神经网络基础

2.神经网络基础

1.神经网络组成部分

1.1 神经网络

（1）神经元

人工神经网络：灵感来自于大脑中的生物神经网络

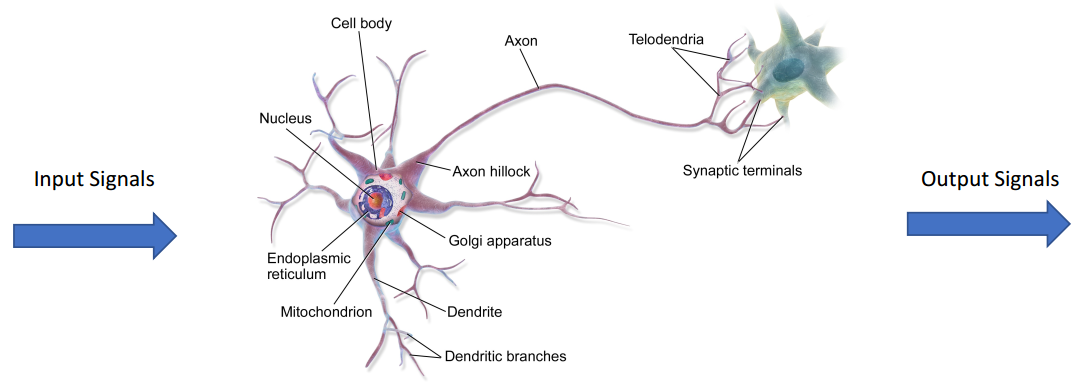
神经元是一个具有输入和一个输出和参数www,bbb的计算单元

hw,b(x)=f(wTx+b) h_{\boldsymbol{w}, b}(\boldsymbol{x})=f\left(\boldsymbol{w}^{T} \boldsymbol{x}+b\right) hw,b(x)=f(wTx+b)

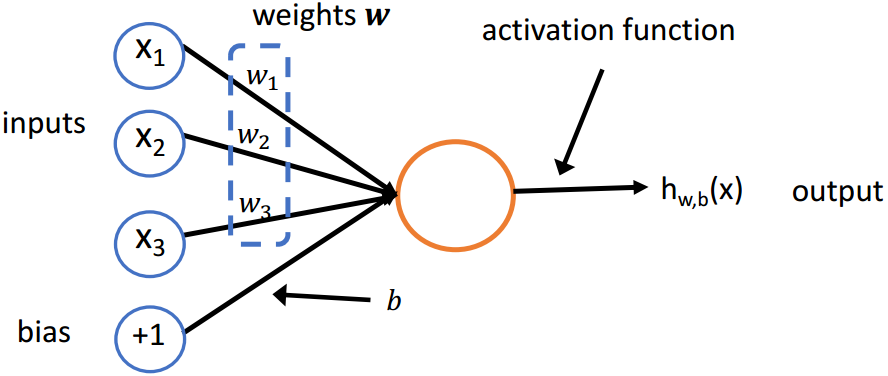
（2）单层神经网络

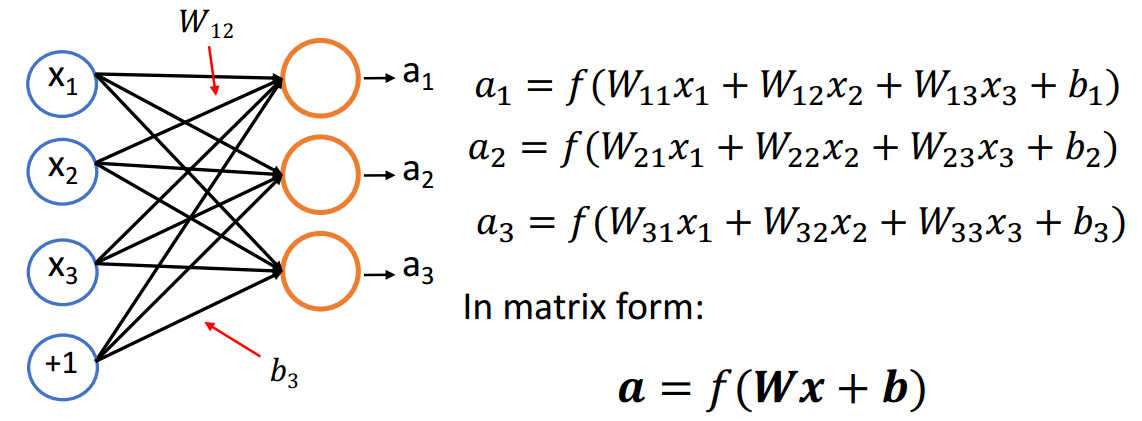
（3）多层神经网络

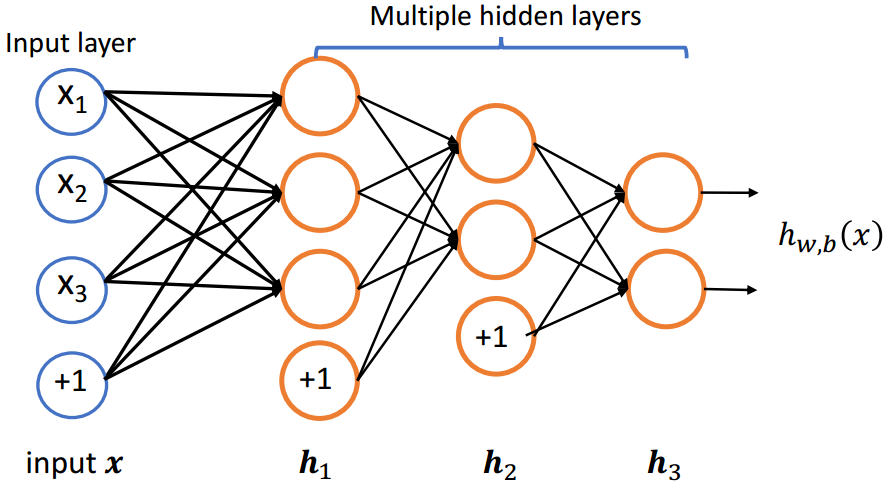
h1=f(W1x+b1)h2=f(W2h1+b2)h3=f(W3h2+b3) \begin{array}{l}\boldsymbol{h}{1}=f\left(\boldsymbol{W}{1} \boldsymbol{x}+\boldsymbol{b}{1}\right) \\ \boldsymbol{h}{2}=f\left(\boldsymbol{W}{2} \boldsymbol{h}{1}+\boldsymbol{b}{2}\right) \\ \boldsymbol{h}{3}=f\left(\boldsymbol{W}{3} \boldsymbol{h}{2}+\boldsymbol{b}_{3}\right)\end{array} h1=f(W1x+b1)h2=f(W2h1+b2)h3=f(W3h2+b3)

1.2 激活函数

如果神经网络中只存在线性运算的话，那么多层的神经网络其实可以被转化为单层的神经网络；所以我们使用非线性的激活函数，防止多层的神经网络塌缩成单一的神经网络

（1）Sigmoid

f(z)=11+e−z f(z)=\frac{1}{1+e^{-z}} f(z)=1+e−z1

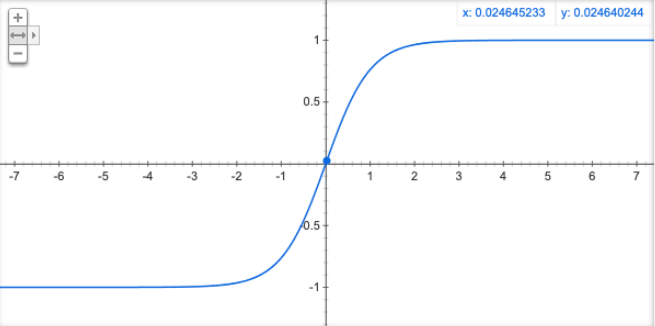
（2）Tanh

f(z)=tanh⁡(z)=ez−e−zez+e−z f(z)=\tanh (z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}} f(z)=tanh(z)=ez+e−zez−e−z

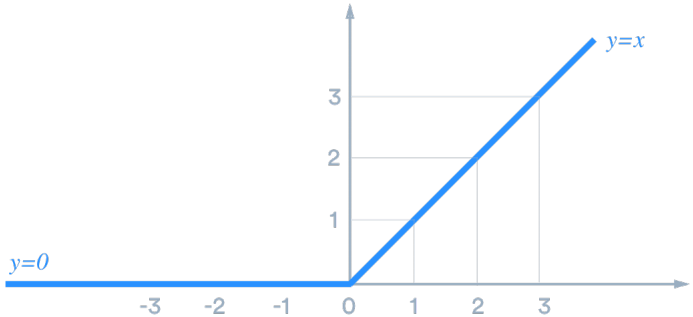
（3）ReLU

f(z)=max⁡(z,0) f(z)=\max (z, 0) f(z)=max(z,0)

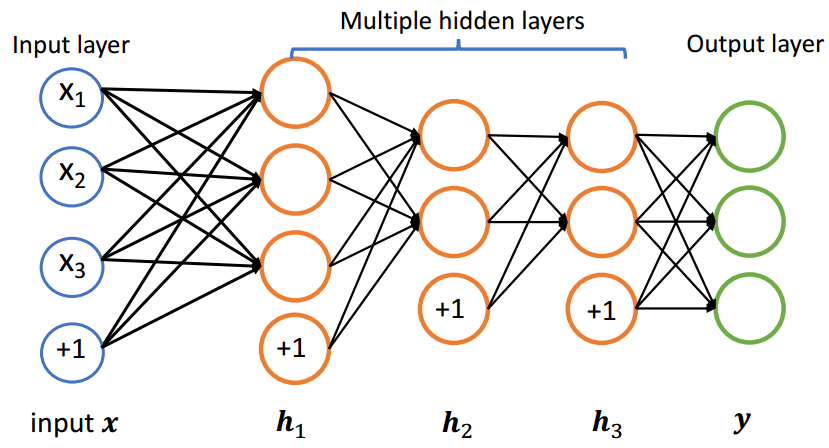
1.3 输出层

增加若干个隐层可以提高网络的表达能力，如果想要得到我们想要的输出结果，就需要添加网络的最后一层，即输出层

2.训练方式

2.1 训练目标

（1）均方根误差

min⁡θJ(θ)=min⁡θ1N∑i=1N(yi−Fθ(xi))2 \min {\theta} J(\theta)=\min {\theta} \frac{1}{N} \sum{i=1}^{N}\left(y{i}-F_{\theta}\left(x_{i}\right)\right)^{2} θminJ(θ)=θminN1i=1∑N(yi−Fθ(xi))2

其中，θ\thetaθ是神经网络参数

（2）交叉熵

min⁡θJ(θ)=min⁡θ−1N∑i=1Nlog⁡Pmodel⁡(Fθ(xi)=yi) \min {\theta} J(\theta)=\min {\theta}-\frac{1}{N} \sum{i=1}^{N} \log P{\operatorname{model}}\left(F_{\theta}\left(x_{i}\right)=y_{i}\right) θminJ(θ)=θmin−N1i=1∑NlogPmodel(Fθ(xi)=yi)

其中，θ\thetaθ是神经网络参数

2.2 随机梯度下降

更新规则：

θnew =θold −α∇θJ(θ) \theta^{\text {new }}=\theta^{\text {old }}-\alpha \nabla_{\theta} \mathrm{J}(\theta) θnew =θold −α∇θJ(θ)

其中，$\alpha

$是学习率

（1）梯度

给定nnn个输入，mmm个输出的函数：

F(x)=[F1(x1,x2...xn),F2(x1,x2...xn)...Fm(x1,x2...xn)] \mathrm{F}(\boldsymbol{x})=\left[F_{1}\left(x_{1}, x_{2} \ldots x_{n}\right), F_{2}\left(x_{1}, x_{2} \ldots x_{n}\right) \ldots F_{m}\left(x_{1}, x_{2} \ldots x_{n}\right)\right] F(x)=[F1(x1,x2...xn),F2(x1,x2...xn)...Fm(x1,x2...xn)]

则输出为m×nm\times nm×n的雅可比矩阵

∂F∂x=[∂F1∂x1⋯∂F1∂xn⋮⋱⋮∂Fm∂x1⋯∂Fm∂xn] \frac{\partial \mathrm{F}}{\partial \boldsymbol{x}}=\left[\begin{array}{ccc}\frac{\partial \mathrm{F}{1}}{\partial x{1}} & \cdots & \frac{\partial \mathrm{F}{1}}{\partial x{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial \mathrm{F}{\mathrm{m}}}{\partial x{1}} & \cdots & \frac{\partial \mathrm{F}{\mathrm{m}}}{\partial x{n}}\end{array}\right] ∂x∂F= ∂x1∂F1⋮∂x1∂Fm⋯⋱⋯∂xn∂F1⋮∂xn∂Fm

其中，(∂F∂x)ij=∂Fi∂xj\left(\frac{\partial \mathrm{F}}{\partial x}\right){i j}=\frac{\partial \mathrm{F}{\mathrm{i}}}{\partial x_{j}}(∂x∂F)ij=∂xj∂Fi表示第i个输出对第j个输入求梯度。

（2）链式求导法则

给定s=uTh,h=f(z),z=Wx+bs=\boldsymbol{u}^{T} \boldsymbol{h}, \boldsymbol{h}=f(\boldsymbol{z}), \boldsymbol{z}=\boldsymbol{W} \boldsymbol{x}+\boldsymbol{b}s=uTh,h=f(z),z=Wx+b，求∂s∂b\frac{\partial s}{\partial \boldsymbol{b}}∂b∂s

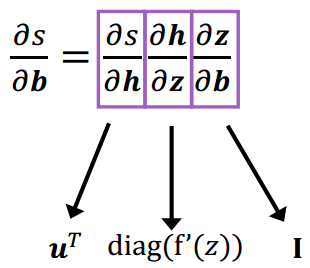
2.3 反向传播

（1）计算图

计算图：将神经网路的传播以图的形式表示。

• 源节点：输入
• 内部节点：操作
• 边传递操作：结果

s=uTh , h=f(z) , z=Wx+b , x input \begin{array}{c}s=\boldsymbol{u}^{T} \boldsymbol{h} ~,~ \boldsymbol{h}=f(\mathbf{z}) ~,~ \boldsymbol{z}=\boldsymbol{W} \boldsymbol{x}+\boldsymbol{b} ~,~ \boldsymbol{x} \text { input }\end{array} s=uTh , h=f(z) , z=Wx+b , x input

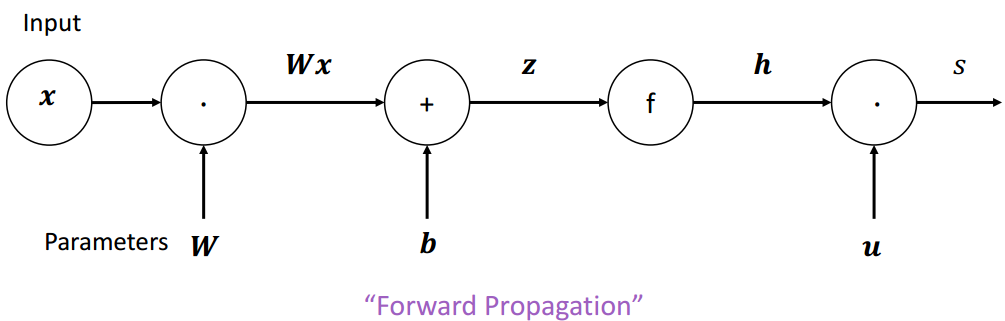
梯度回传：沿着边往回走，沿着梯度传递

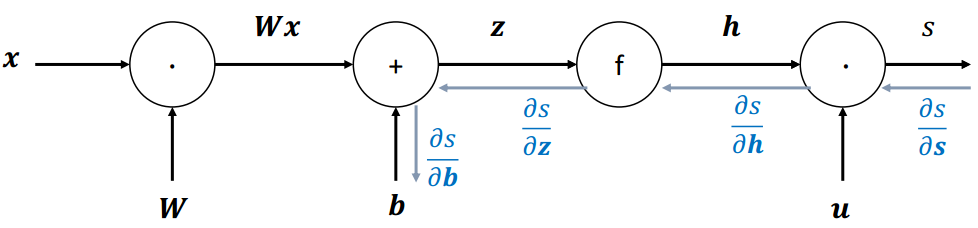
（2）单个结点

节点接收到一个"上游梯度"

目标是传递正确的"下游梯度"

每个节点都有一个局部梯度（ local gradient ），输出相对于输入的梯度

downstreamgradient\]=\[upstreamgradient\]×\[localgradient\] \[downstream gradient\] = \[upstream gradient\] \\times \[local gradient\] \[downstreamgradient\]=\[upstreamgradient\]×\[localgradient

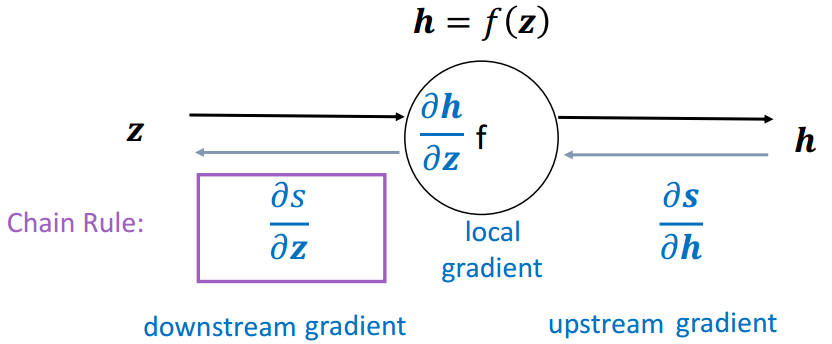
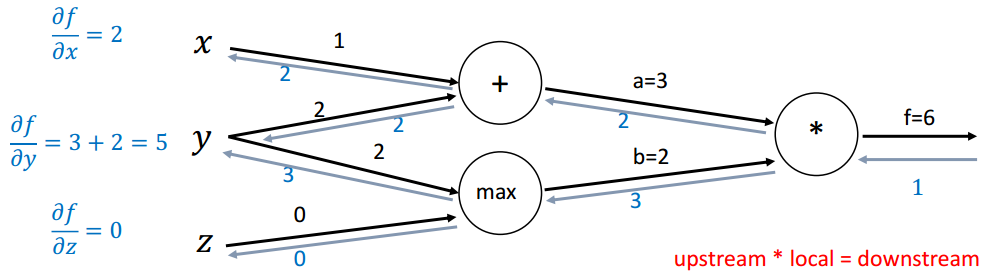
（3）示例

函数：f(x,y,z)=(x+y)max⁡(y,z) , x=1,y=2,z=0\begin{array}{c}f(x, y, z)=(x+y) \max (y, z) ~~,~~ x=1, y=2, z=0\end{array}f(x,y,z)=(x+y)max(y,z) , x=1,y=2,z=0

前向传播：

a=x+y=3 b=max⁡(y,z)=2f=ab=6 \begin{array}{c}a=x+y=3 \\ \mathrm{~b}=\max (y, z)=2 \\ f=a b=6\end{array} a=x+y=3 b=max(y,z)=2f=ab=6

本地梯度（Local gradients）：

∂a∂x=1,∂a∂y=1∂b∂y=1(y>z)=1,∂b∂z=1(z>y)=0∂f∂a=b=2,∂f∂b=a=3 \begin{array}{c}\frac{\partial a}{\partial x}=1, \frac{\partial a}{\partial y}=1 \\ \frac{\partial b}{\partial y}=\mathbf{1}(y>z)=1, \frac{\partial b}{\partial z}=\mathbf{1}(z>y)=0 \\ \frac{\partial f}{\partial a}=b=2, \frac{\partial f}{\partial b}=a=3\end{array} ∂x∂a=1,∂y∂a=1∂y∂b=1(y>z)=1,∂z∂b=1(z>y)=0∂a∂f=b=2,∂b∂f=a=3

初始计算图：

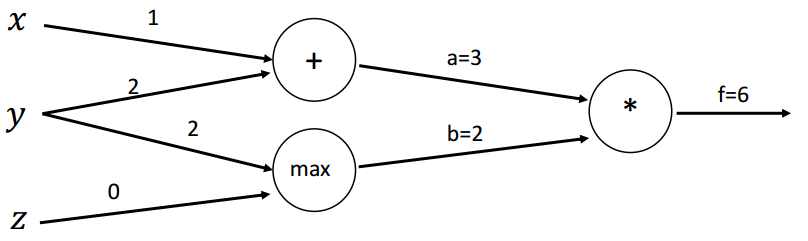
回传第一步：

回传第二步（*）：

∂f∂a=b=2,∂f∂b=a=3 \frac{\partial f}{\partial a}=b=2, \frac{\partial f}{\partial b}=a=3 ∂a∂f=b=2,∂b∂f=a=3

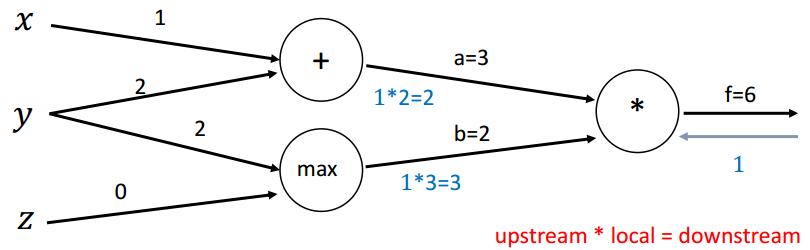
回传第三步（max）：

∂b∂y=1(y>z)=1,∂b∂z=1(z>y)=0 \frac{\partial b}{\partial y}=\mathbf{1}(y>z)=1, \frac{\partial b}{\partial z}=\mathbf{1}(z>y)=0 ∂y∂b=1(y>z)=1,∂z∂b=1(z>y)=0

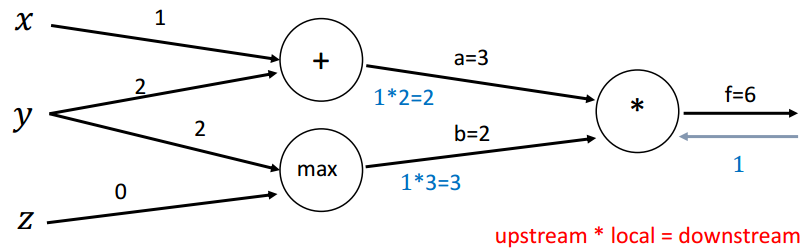
回传第四步（+）：

∂a∂x=1,∂a∂y=1 \frac{\partial a}{\partial x}=1, \frac{\partial a}{\partial y}=1 ∂x∂a=1,∂y∂a=1

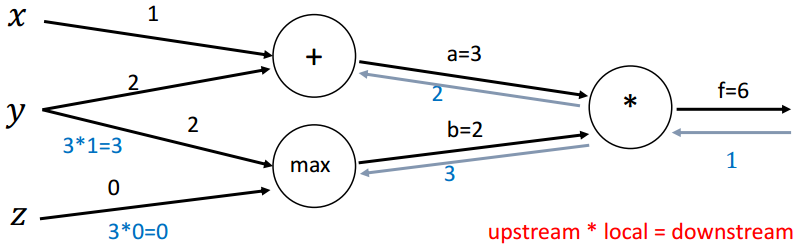
计算最终梯度：

3.词表示：Word2Vec

Word2Vec：可以学到一些语义内涵，捕捉到语言学上的一些规律

3.1 Word2Vec

Word2vec使用浅层神经网络将单词与分布式表示相关联

它可以捕获许多语言规则，例如:

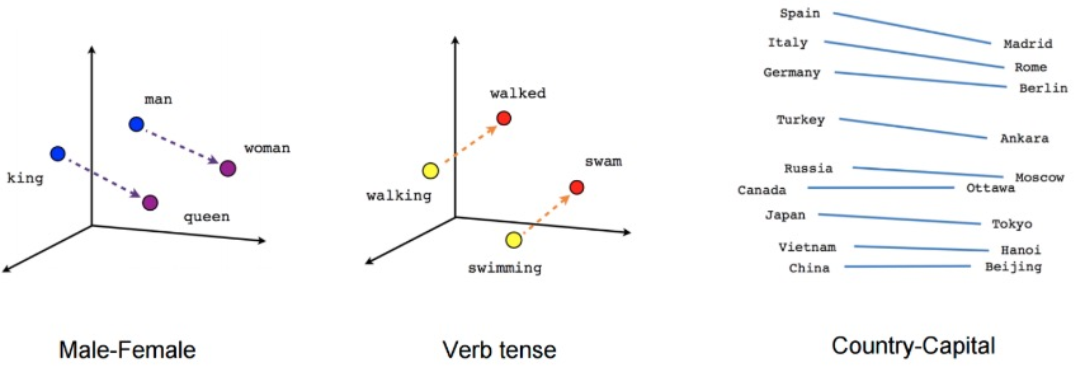
Word2vec可以利用两种架构来生成单词的分布式表示：

• Continuous bag-of-words (CBOW)
• Continuous skip-gram

3.2 滑动窗口

Word2vec使用一个固定大小的滑动窗口沿着句子移动

• 在每个窗口中，中间的单词是目标单词，其他单词是上下文单词
• 给定上下文单词，CBOW预测目标单词的概率
• 当给定目标词时，skip-gram预测上下文词的概率

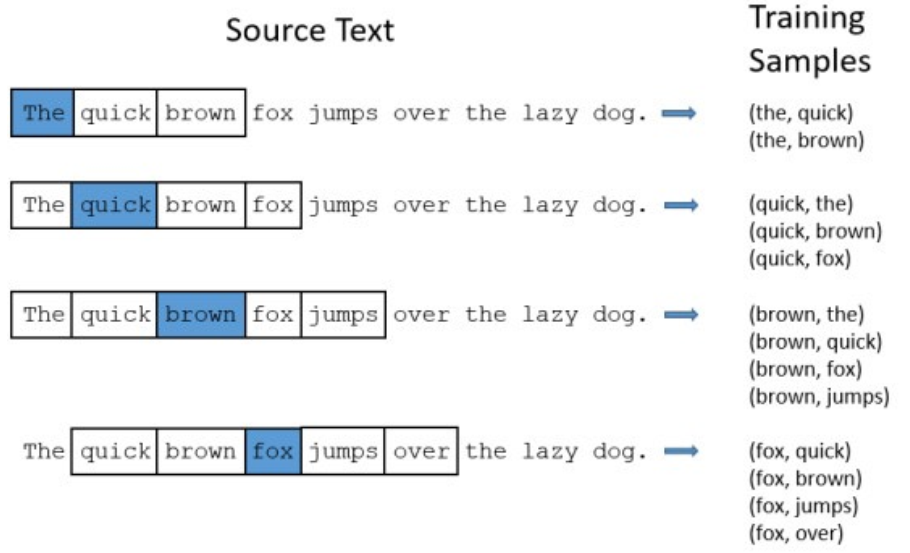
滑动窗口大小为5

3.3 CBOW（Continuous Bag-of-Words）

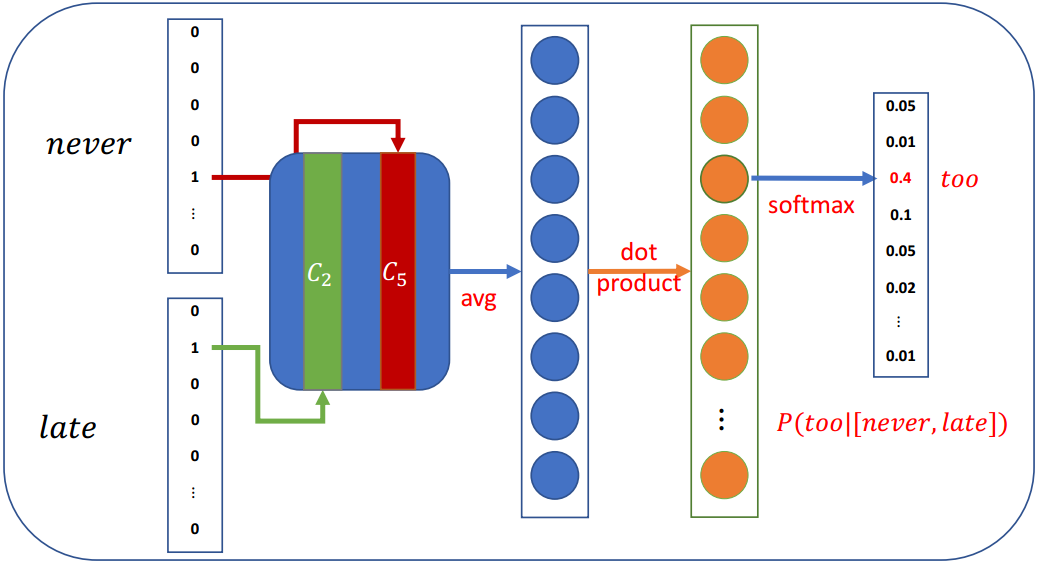
在CBOW架构中，该模型给出一个周围上下文词的窗口来预测目标词

• 根据词袋假设：上下文词的顺序不影响预测
• 假设窗口大小为5，Never too late to learn

P(late∣[never,too,to,learn]) P( late \mid[ never, too, to, learn ]) P(late∣[never,too,to,learn])

3.4 Continuous Skip-Gram

在skip-gram架构中，该模型从目标词中预测上下文词

假设窗口大小为5，Never too late to learn

P([too,late]∣Never),P([Never,late,to]∣too),... P([ too, late ] \mid Never ), P([ Never, late, to ] \mid too ), \ldots P([too,late]∣Never),P([Never,late,to]∣too),...

Skip-gram每步预测一个上下文词，训练样本为:

P( too ∣ Never ),P( late ∣ Never ),P( Never ∣ too ),P( late ∣ too ),P( to ∣ too ),... \begin{array}{l}P(\text { too } \mid \text { Never }), P(\text { late } \mid \text { Never }), P(\text { Never } \mid \text { too }), P(\text { late } \mid \text { too }), P(\text { to } \mid \text { too }), \ldots\end{array} P( too ∣ Never ),P( late ∣ Never ),P( Never ∣ too ),P( late ∣ too ),P( to ∣ too ),...

3.5 Softmax存在问题

当词汇量很大的时候

• Softmax对所有单词的每一步都依赖于大量的模型参数，这在计算上是不切实际的
• 我们需要提高计算效率

事实上，在word2vec中我们并不需要一个完整的概率模型；word2vec主要有两种改进方法:

• 负采样
• 分层softmax

3.6 负采样

当词汇表非常大，这意味着模型每一步都有大量的权重需要更新

负抽样的思想是，每一步只更新一小部分权重

既然有词汇表并且知道上下文单词，可以按概率选择几个不在上下文单词列表中的单词：

P(wi)=f(wi)3/4∑j=1Vf(wj)3/4 P\left(w_{i}\right)=\frac{f\left(w_{i}\right)^{3 / 4}}{\sum_{j=1}^{V} f\left(w_{j}\right)^{3 / 4}} P(wi)=∑j=1Vf(wj)3/4f(wi)3/4

其中，f(wi)f(w_i)f(wi)为wiw_iwi的频次，3/43/43/4为经验值

相比于f(wi)∑j=1Vf(wj)\frac{f\left(w_{i}\right)}{\sum_{j=1}^{V} f\left(w_{j}\right)}∑j=1Vf(wj)f(wi)，这可以增加低频词出现的概率。

假设我们只选取4个负采样词：

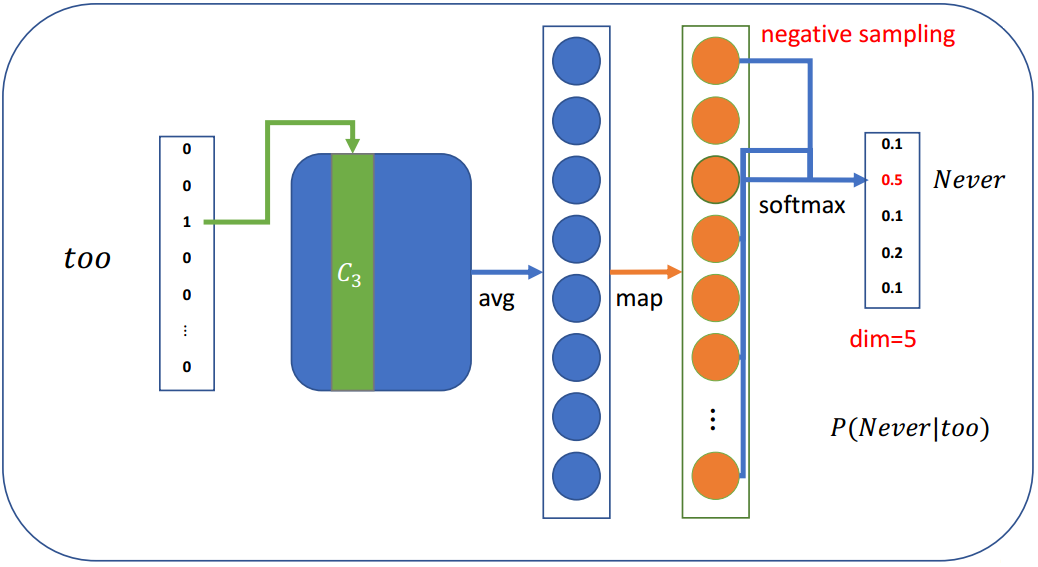
然后我们可以计算损失，并优化每一步的权重(不是所有的权重)

• 假设有一个大小为300×10,000的权重矩阵，输出大小为5
• 只需要更新300×5权重，这只占所有权重的0.05%

3.7 其他一些细节

（1）Sub-Sampling

罕见的单词可能更有可能携带不同的信息，据此，Sub-Sampling有概率地丢弃单词:

1−t/f(w) 1-\sqrt{t / f(w)} 1−t/f(w)

其中，f(w)f(w)f(w)为单词频率，ttt是一个可调节的阈值吗

（2）Soft sliding window

滑动窗口应该给较远的单词分配较少的权重

将滑动窗口最大的定义为 SmaxS_{max}Smax，实际的滑动窗口大小在1和SmaxS_{max}Smax之间随机选择

因此，那些靠近目标单词的单词更有可能出现在窗口中

4.通用神经网络

4.1 RNN

（1）顺序记忆

RNN的关键概念：处理序列数据时的顺序存储器

定义：一种让大脑更容易识别序列模式的机制

RNN递归地更新序列内存以建模序列数据

（2）RNN

（3）RNN单元

hi=tanh⁡(Wxxi+Whhi−1+b)yi=F(hi) \begin{array}{c}h_{i}=\tanh \left(W_{x} x_{i}+W_{h} h_{i-1}+b\right) \\ y_{i}=F\left(h_{i}\right)\end{array} hi=tanh(Wxxi+Whhi−1+b)yi=F(hi)

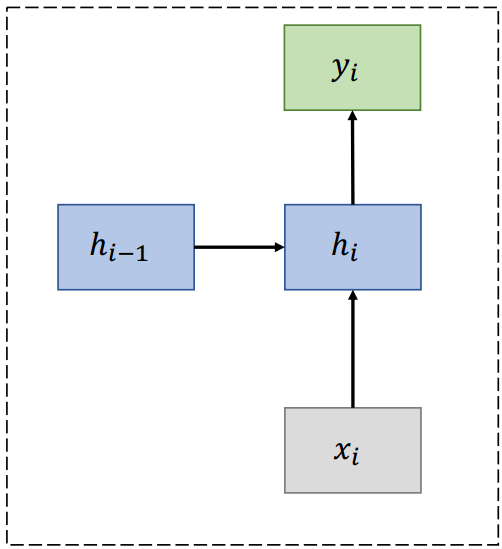
（4）RNN语言模型

WhW_hWh参数是共享的

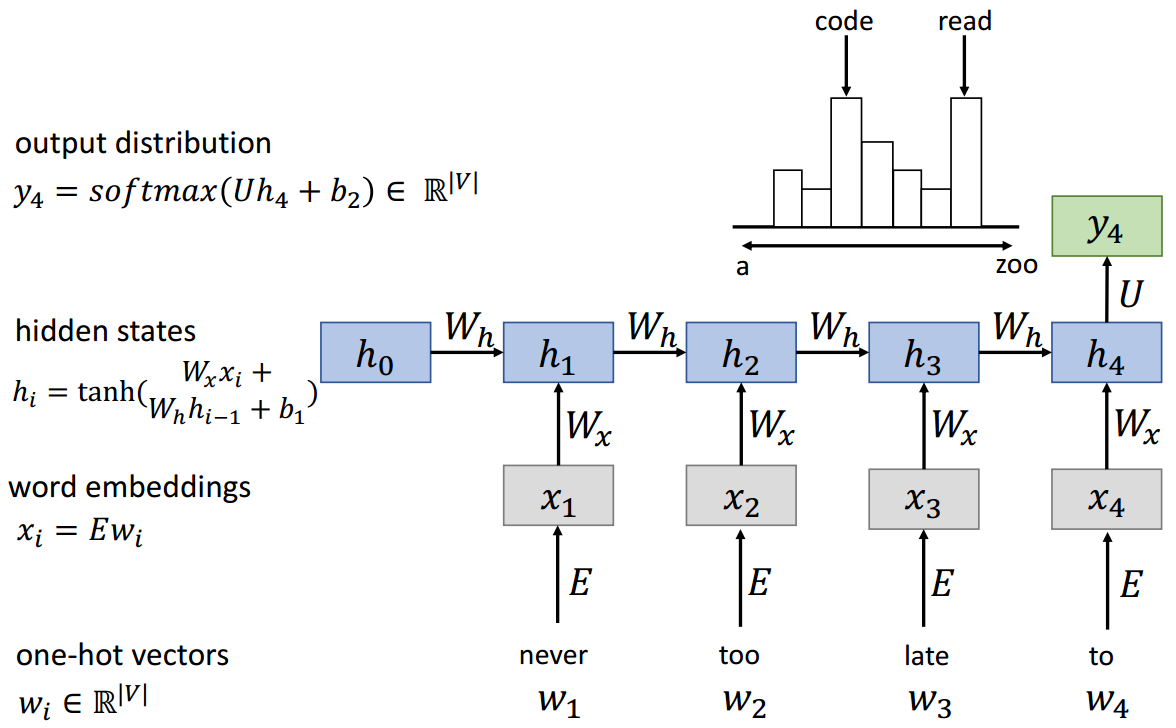
（5）优缺点

优点：

• 可以处理任何长度的输入
• 模型尺寸不增加较长的输入
• 跨时间步共享权重
• 从许多后退步骤计算步骤

缺点：

• 循环计算速度慢
• 在实践中，很难从许多步骤中获取信息

（6）梯度问题

RNN链比较长，容易出现梯度消失或爆炸

hi=tanh⁡(Wxxi+Whhi−1+b) h_{i}=\tanh \left(W_{x} x_{i}+W_{h} h_{i-1}+b\right) hi=tanh(Wxxi+Whhi−1+b)

Δw1=∂ Loss ∂w2=∂ Loss ∂hn∂hn∂hn−1∂hn−1∂hn−2...∂h3∂h2∂h2∂w2 \Delta w_{1}=\frac{\partial \text { Loss }}{\partial w_{2}}=\frac{\partial \text { Loss }}{\partial h_{n}} \frac{\partial h_{n}}{\partial h_{n-1}} \frac{\partial h_{n-1}}{\partial h_{n-2}} \ldots \frac{\partial h_{3}}{\partial h_{2}} \frac{\partial h_{2}}{\partial w_{2}} Δw1=∂w2∂ Loss =∂hn∂ Loss ∂hn−1∂hn∂hn−2∂hn−1...∂h2∂h3∂w2∂h2

（7）RNN变种

梯度消失问题的主要解决方案是在递归中使用更复杂的隐单元计算

• GRU
• LSTM

主要思想：保持记忆，捕捉远距离的依赖

4.2 GRU（Gated Recurrent Unit）

Vanilla RNN在下一个时间步直接计算隐藏层：

hi=tanh⁡(Wxxi+Whhi−1+b) h_{i}=\tanh \left(W_{x} x_{i}+W_{h} h_{i-1}+b\right) hi=tanh(Wxxi+Whhi−1+b)

在原始RNN中，增加门控机制，主要用于平衡过去的信息和输入之间的影响。主要有两个门控单元：

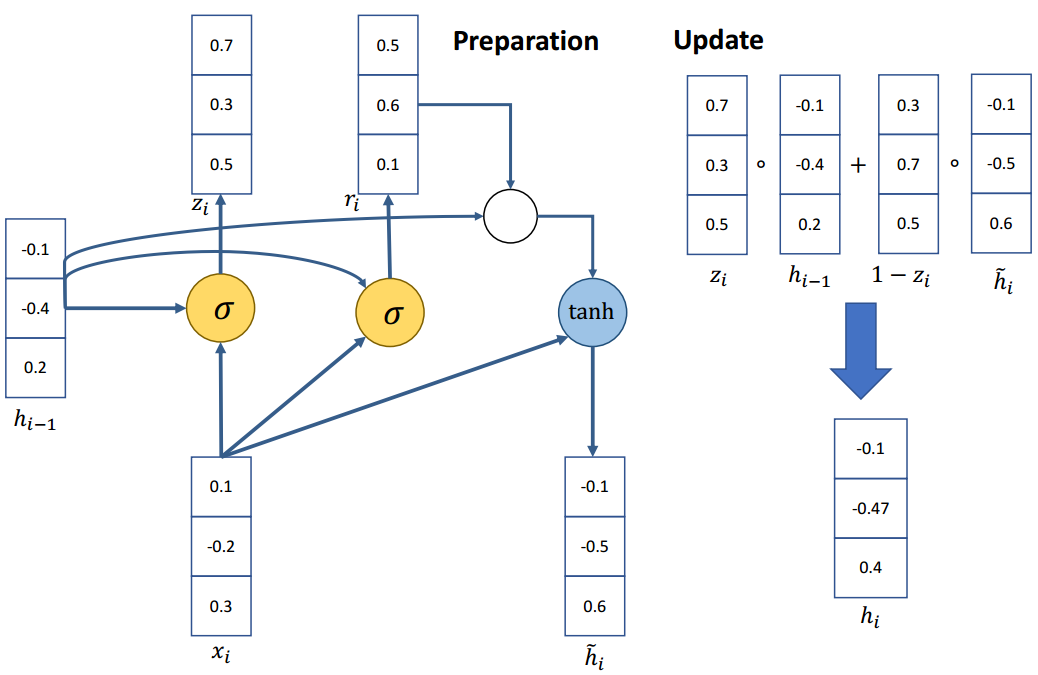
更新门 （update gate）：zi=σ(Wx(z)xi+Wh(z)hi−1+b(z))z_{i}=\sigma\left(W_{x}^{(z)} x_{i}+W_{h}^{(z)} h_{i-1}+b^{(z)}\right)zi=σ(Wx(z)xi+Wh(z)hi−1+b(z))

重置门 （reset gate）：ri=σ(Wx(r)xi+Wh(r)hi−1+b(r))r_{i}=\sigma\left(W_{x}^{(r)} x_{i}+W_{h}^{(r)} h_{i-1}+b^{(r)}\right)ri=σ(Wx(r)xi+Wh(r)hi−1+b(r))

新的激活输出 h~i\tilde{h}{i}h~i：h~i=tanh⁡(Wxxi+ri∗Whhi−1+b)\tilde{h}{i}=\tanh \left(W_{x} x_{i}+r_{i} * W_{h} h_{i-1}+b\right)h~i=tanh(Wxxi+ri∗Whhi−1+b)

最后的隐藏单元输出hih_ihi：hi=zi∗hi−1+(1−zi)∗h~ih_{i}=z_{i} * h_{i-1}+\left(1-z_{i}\right) * \tilde{h}_{i}hi=zi∗hi−1+(1−zi)∗h~i

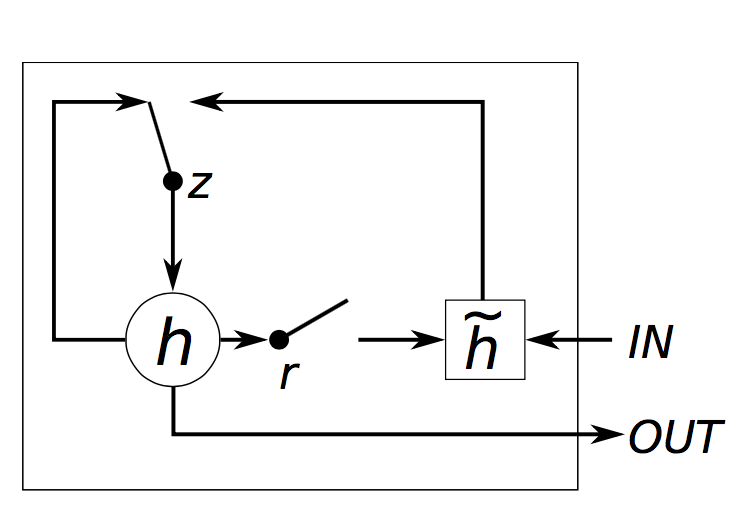
示例

如果重置门rir_iri 接近于0

h~i≈tanh⁡(Wxxi+0∗Whhi−1+b) \tilde{h}{i} \approx \tanh \left(W{x} x_{i}+0 * W_{h} h_{i-1}+b\right) h~i≈tanh(Wxxi+0∗Whhi−1+b)

h~i≈tanh⁡(Wxxi+b) \tilde{h}{i} \approx \tanh \left(W{x} x_{i}+b\right) h~i≈tanh(Wxxi+b)

忽略先前的隐藏状态，这表明当前的激活与过去无关。例如，在一篇新文章的开头，过去的信息对于当前的激活是无用的。

更新门ziz_izi控制与当前激活相比，过去的状态有多少是重要的。

如果ziz_izi接近于1，然后可以通过许多时间步骤复制该单元中的信息!

hi=1∗hi−1+(1−1)∗h~i=hi−1 h_{i}=1 * h_{i-1}+(1-1) * \tilde{h}{i}=h{i-1} hi=1∗hi−1+(1−1)∗h~i=hi−1

如果ziz_izi接近于0，然后将信息放入该单元并完全取代历史信息

4.3 LSTM（Long Short-Term Memory network）

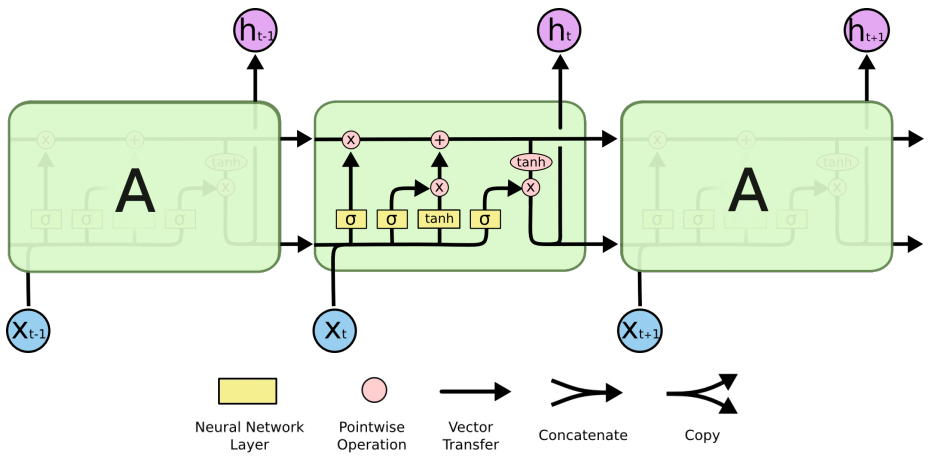
LSTM是一种特殊的RNN，能够像GRU一样学习长期依赖关系；

（1）状态单元 CtC_tCt

LSTM的关键是单元状态CtC_tCt

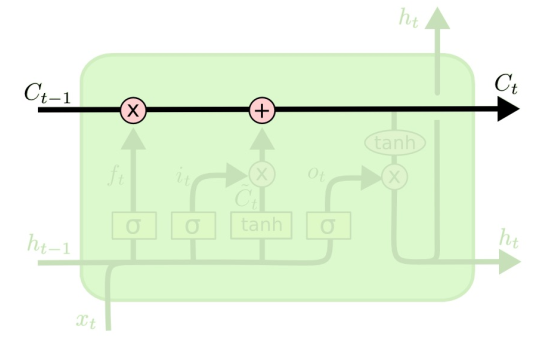
• 用于捕获长期依赖的额外向量
• 直接贯穿整个链条，只有少量的线性交互作用
• 易于删除或添加信息到细胞状态

（2）遗忘门ftf_tft

遗忘门：决定从状态单元中丢弃哪些信息

ft=σ(Wf⋅[ht−1,xt]+bf) f_{t}=\sigma\left(W_{f} \cdot\left[h_{t-1}, x_{t}\right]+b_{f}\right) ft=σ(Wf⋅[ht−1,xt]+bf)

其中，[ht−1,xt]\left[h_{t-1}, x_{t}\right][ht−1,xt]为拼接向量

如果ft=0f_{t}=0ft=0，则直接遗忘过去的信息。

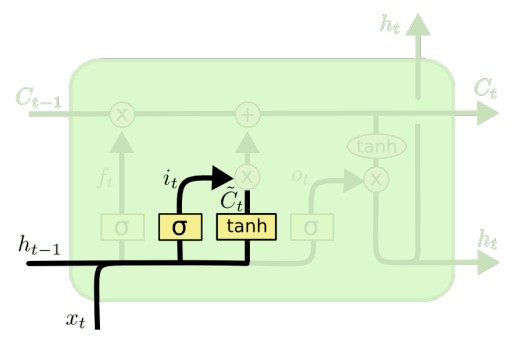
（3）输入门 iti_tit

输入门：决定在单元状态中存储什么信息；

输入门iti_tit和新的候选状态信息 C~t\tilde{C}_{t}C~t

it=σ(Wi⋅[ht−1,xt]+bi) i_{t}=\sigma\left(W_{i} \cdot\left[h_{t-1}, x_{t}\right]+b_{i}\right) it=σ(Wi⋅[ht−1,xt]+bi)

C~t=tanh⁡(WC⋅[ht−1,xt]+bC) \tilde{C}{t}=\tanh \left(W{C} \cdot\left[h_{t-1}, x_{t}\right]+b_{C}\right) C~t=tanh(WC⋅[ht−1,xt]+bC)

更新就的状态信息 Ct−1C_{t-1}Ct−1，结合前两步的结果

Ct=ft∗Ct−1+it∗C~t C_{t}=f_{t} * C_{t-1}+i_{t} * \tilde{C}_{t} Ct=ft∗Ct−1+it∗C~t

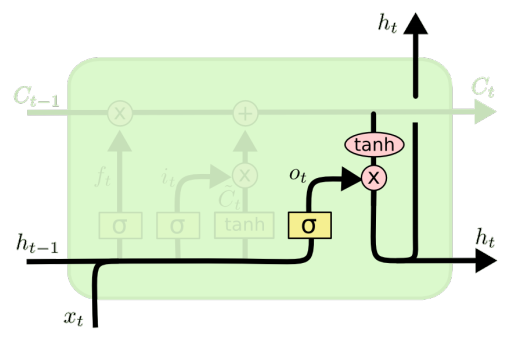
（4）输出门oto_tot

输出门：决定输出什么信息

为特定的单词表示调整句子信息

ot=σ(Wo[ht−1,xt]+bo) o_{t}=\sigma\left(W_{o}\left[h_{t-1}, x_{t}\right]+b_{o}\right) ot=σ(Wo[ht−1,xt]+bo)

ht=ot∗tanh⁡(Ct) h_{t}=o_{t} * \tanh \left(C_{t}\right) ht=ot∗tanh(Ct)

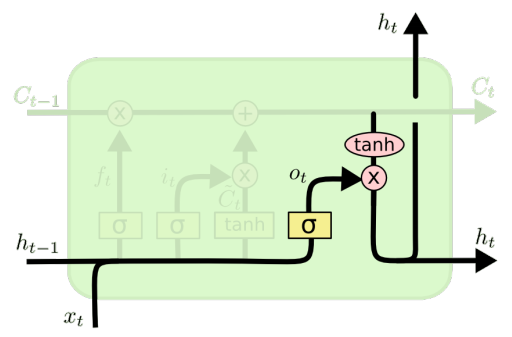
功能强大，特别是当堆叠和更深层时(每个隐藏层已经由深层内部网络计算)

如果你有大量的数据，非常有用

4.4 双向RNN

在传统的RNN中，当前状态只捕获过去的信息

ht=f(xt−1,...,x2,x1) h_{t}=f\left(x_{t-1}, \ldots, x_{2}, x_{1}\right) ht=f(xt−1,...,x2,x1)

问题：在很多应用中，我们希望输出yty_tyt依赖于整个输入序列

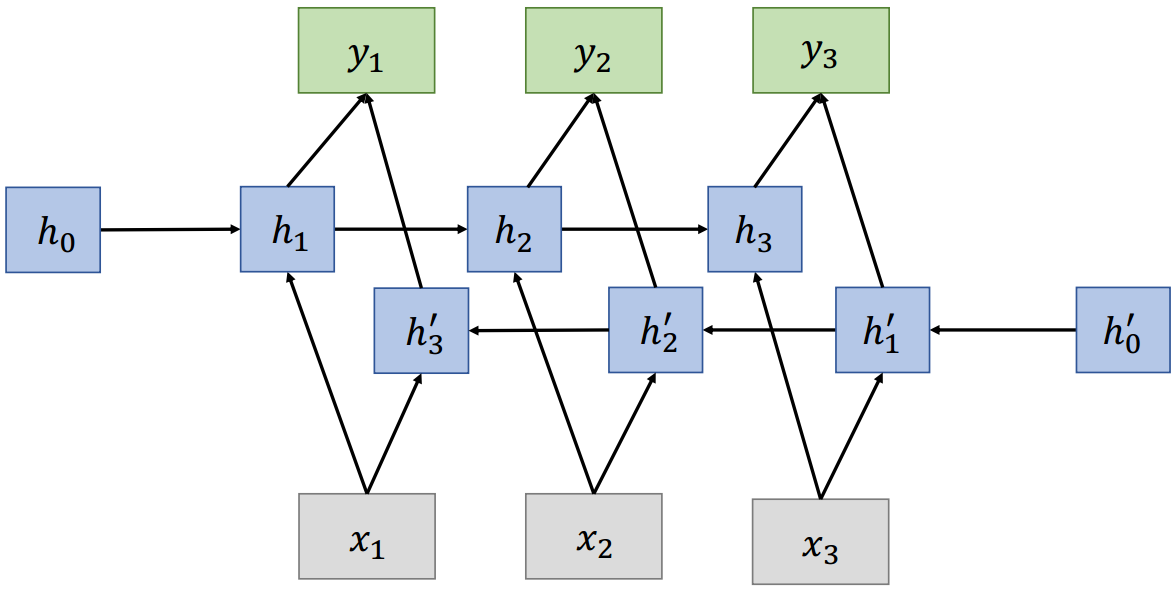
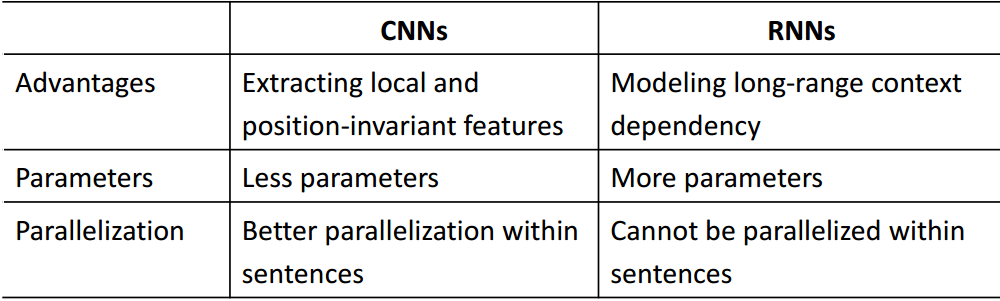
4.5 CNN

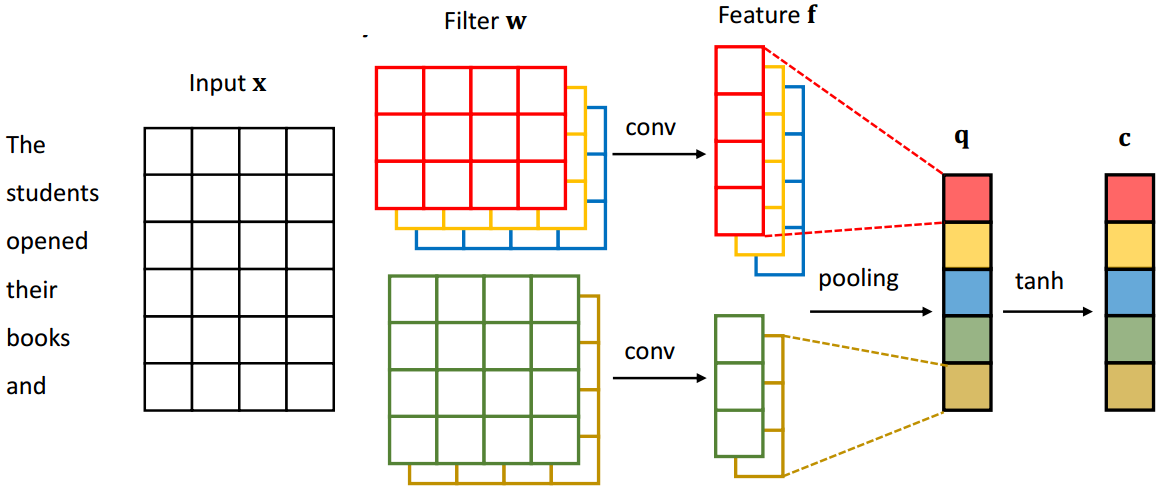
RNN vs CNN