一、实践中的高斯消元法
数值线性代数的一个目标就是快速兼顾精度的求解。我们需要效率,但是也要避免不稳定性。在高斯消元法(Gaussian elimination)中,需要权衡如何交换方程的顺序 。本节说明了什么时候为了计算的速度交换行,什么时候为了计算精度而交换行。
精确求解的关键是要避免不必要的很大的数,通常也要求避免很小的数!小的主元意味着需要大的乘数(因为消元时要除以该主元)。一个好的方法是 "部分(列)主元消元法 partial pivoting ",基本思想就是每一步选择一个绝对值最大的元素,然后通过行变换将其交换至主元的位置上,再用它消去主对角线以下的元素。下面会说明为什么在计算机程序中要使用这种消元策略。
也可以进行其它的行交换来减少消元步骤。在实践上,大部分高阶矩阵都是稀疏的(sparse) ------ 绝大部分元素都为零。当方程重新排列后产生非零窄带状系数时,消元速度最快,在消元过程中,如果窄带内的零元素被填充为了非零元,那么这些零元就被破坏了,这样就无法节省计算时间。
11.211.211.2 节是关于数值稳定性,它是所求解问题自带的属性,通过 "条件数(condition number) " 来衡量。11.311.311.3 节介绍如何通过迭代法(iterations) 来求解 Ax=bA\boldsymbol x=\boldsymbol bAx=b. 不同于直接消元,计算机通过重复计算一组更简单的式子来逼近答案,由每一步的迭代值 xk\boldsymbol x_kxk 推出下一步的迭代值 xk+1\boldsymbol x_{k+1}xk+1. 好的迭代法(如共轭梯度法 conjugate gradient method ),xk\boldsymbol x_kxk 会很快收敛到 x=A−1b\boldsymbol x=A^{-1}\boldsymbol bx=A−1b.
二、最快的超级计算机
200820082008 年 555 月 202020 日,IBM(International Business Machine,国际商用公司)和 Los Alamos 宣布了一项新的超算纪录,走鹃(Roadrunner)超级计算机是第一个实现每秒千万亿次(101510^{15}1015)浮点运算的机器:1 petaflop1\,petaflop1petaflop 超级计算机。这个世界纪录的排名标准是基于求解一个超大规模且稠密的线性方程组 Ax=bA\boldsymbol x=\boldsymbol bAx=b 的速度:计算机的计算速度是由线性代数来测试的。
这一台机器在 201320132013 年就停止了运行!TOP500(全球超级计算机排行榜)项目列出了世界上最强大的 500500500 个计算机系统。截止 201520152015 年 101010 月,前四名分别是来自中国的国防科技大学(NUDT),美国的克雷(Cray)和 IBM,和日本的富士通(Fujitsu). 它们都使用基于 LINUX 的系统,所有的向量处理器都跌出了 TOP500.
展望未来的话,Summit 预计会以 150−300150-300150−300 petaflops 排名第一,而奥巴马下令卡法百亿亿次系统(1000 petaflops). 到目前为止,我们遵循的是每 141414 个月翻一倍的摩尔定律(Moore's Law).
LAPACK 软件使用的是列主元消元法,与我们所介绍的最大的不同是,它使用的是大型子矩阵而不是单个数字运算。现在,更依赖的是图像处理单元(GPU's),视频游戏市场要比科学计算领域更加庞大,这也加速了芯片的发展。
在 IBM 的蓝色基因(BlueGene)前,建造一台千万亿次机器需要 320003200032000 个标准四核处理器,而蓝色基因所使用的新架构大大降低了芯片功率,但是它也有代价:一段代码需要三个独立的编译器和显式指令来传输所有数据。有兴趣可以查阅 SIAM News(2008 年 7 月)的优秀文章。
对矩阵计算的研究结果体现在高度优化的 BLAS(Basic Linear Algebra Subroutines,基础线性代数子程序)中,它们有三个等级的运算:
- Level 1 向量的线性组合 au+va\boldsymbol u+\boldsymbol vau+v:算法的时间复杂度为 O(n)O(n)O(n)
- Level 2 矩阵 - 向量乘法 Au+vA\boldsymbol u+\boldsymbol vAu+v:算法的时间复杂度为 O(n2)O(n^2)O(n2)
- Level 3 矩阵 - 矩阵乘法 AB+CAB+CAB+C:算法的时间复杂度为 O(n3)O(n^3)O(n3)
Level 1 是一个消元步骤(行 iii 减去 lijl_{ij}lij 乘行 jjj);Level 2 可以一次消去一整行;高性能的求解器更多地位于 Level 3 BLAS(ABABAB 有 2n32n^32n3 次浮点运算和 2n22n^22n2 个数据)。
限制并行计算速度的是数据通信和存储检索(storage retrieval)的效率,主内存和浮点计算芯片之间的高速缓存一定充分利用!分块矩阵方法(block matrix approach) 消元才能获得最高的速度。
未来即将发生的重大变化就是引入芯片级的并行处理。
三、舍入误差与列主元
到目前为止,我们接受任意的非零主元,然而实际上,绝对值很小的主元可能会比较危险,会出现较大的误差。当我们将两个不同数量级的数相加时,很有可能会出现不准确的情况。计算机使用的是固定位数(fixed number)的有效数字(例如,一个性能非常低的计算机使用的是三位有效数字),那么 10000+110000+110000+1 将被舍入(rounded off)为 100001000010000,此时 "1""1""1" 将会被完全丢弃了。下面我们看一下这个问题的解将会发生怎样的变化:0.0001u+v=1−u+v=0的系数矩阵是A=[0.00011−11]\begin{array}{r}0.0001u+v=1\\-u+v=0\end{array}\kern 15pt的系数矩阵是\kern 10ptA=\begin{bmatrix}0.0001&1\\-1&1\end{bmatrix}0.0001u+v=1−u+v=0的系数矩阵是A=[0.0001−111]如果我们将 0.00010.00010.0001 作为主元,那么消元时我们会将第 111 行乘上 10 00010\,00010000 然后加到第 222 行,四舍五入后得到:10 000v=10 000而不是10 001v=10 00010\,000v=10\,000\kern 15pt而不是\kern 15pt10\,001v=10\,00010000v=10000而不是10001v=10000那么计算机的答案是 v=1v=1v=1,虽然与实际解 v=0.9999v=0.9999v=0.9999 很接近,但是我们把这个近似解 v=1v=1v=1 回代到方程来求 uuu :
0.0001u+1=1而不是0.0001u+0.9999=10.0001u+1=1\kern 15pt而不是\kern 15pt0.0001u+0.9999=10.0001u+1=1而不是0.0001u+0.9999=1
第一个方程的解得到的是 u=0u=0u=0,而正确的解(第二个方程)是 u=1.000u=1.000u=1.000. 我们在矩阵中仅在主元中舍去了 "1""1""1",就得到了一个错误的答案。从 10 001\pmb{10\,001}10001 到 10,000\pmb{10,000}10,000 这样小的变化就将答案从 u=1\pmb{u=1}u=1 变成了 u=0\pmb{u=0}u=0 了 (100%100\%100% 错误!)
如果我们交换一下行,即使是这个性能很弱的只能有 333 位有效数字的计算机也可以得到正确答案:−u+v=00.0001u+v=1→−u+v=0v=1→u=1v=1\begin{array}{r}-u+v=0\\0.0001u+v=1\end{array}\kern 5pt\rightarrow\kern 5pt\begin{array}{r}-u+v=0\\v=1\end{array}\kern 5pt\rightarrow\kern 5pt\begin{array}{r}u=1\\v=1\end{array}−u+v=00.0001u+v=1→−u+v=0v=1→u=1v=1原先方程的主元是 0.00010.00010.0001 和 10 00010\,00010000 ------ 数值的比例很大,而进行行交换后,主元变为了 −1-1−1 和 1.00011.00011.0001 ------ 比值很接近。此时计算机计算时使用的近似主元是 −1-1−1 和 111,它们与真实的主元很接近。绝对值过小的主元会带来数值的不稳定性,而修正措施就是部分(列)主元消元法(partial pivoting) . 下面是我们在消元进行至第 kkk 列时选取最佳主元的策略:在第 k 行和它下面所有的元素中选择绝对值最大的数,将其所在的行与第 k 行交换。\pmb{在第\,k\,行和它下面所有的元素中选择绝对值最大的数,将其所在的行与第\,k\,行交换。}在第k行和它下面所有的元素中选择绝对值最大的数,将其所在的行与第k行交换。全主元消元法(complete pivoting)的策略是同时在后续的列中寻找绝对值最大的元素,它不仅需要进行行交换,还要进行列交换,但是这种方法由于复杂很多而很少使用,主流的程序中都是使用部分主元消元法。对某一行或某一列乘上一个常缩放系数也是一个很好的策略。例如,原先的第一个方程两边同时乘上 10 00010\,00010000,就变成了 u+10 000v=10 000u+10\,000v=10\,000u+10000v=10000,此时将不需要缩放,虽然 111 看上去是一个很好的主元,但是这样也可能会错过必要的行交换。
对于正定的系数矩阵,并不需要行交换,此时消元过程中出现的主元都可以接受,虽说小的主元可能会出现,但是行交换也不会改善矩阵。当矩阵的条件数很大时,问题出现在矩阵本身而不是代码上,这种情况下,输出的结果对输入的敏感将会无可避免。
我们现在理解了计算机实际上是如何求解线性方程组 Ax=bA\boldsymbol x=\boldsymbol bAx=b ------ 通过部分消元法 。对比一下理论的求解方法 ------ 求 A−1A^{-1}A−1,然后做乘法 A−1bA^{-1}\boldsymbol bA−1b,描述细节需要更多的时间。但是计算机计算时,消元要快很多。消元法应该也是研究矩阵的行空间和零空间代数结构的最佳方法。
四、操作次数:稠密矩阵
下面讨论实际计算量的问题:利用消元法求解 Ax=bA\boldsymbol x=\boldsymbol bAx=b 需要多少次运算?这个决定了我们能够解决多大规模的问题。
首先考虑 nnn 阶矩阵 AAA 消元得到矩阵 UUU 这个过程。当我们从第 222 行减去第 111 行的倍数时,我们需要进行 nnn 次运算。第一步是除以主元,求得乘数 lll,对于该行的其它 n−1n-1n−1 个元素,我们执行 "乘-减(multiply-subtract)" 运算。为了方便,我们将这视为一个运算。如果我们把乘以乘数 lll 和减去这一行的结果视为两个运算的话,将所有的运算次数乘 222 即可。
矩阵 AAA 是 n×nn\times nn×n 的方阵,上述的计算数量可以适用于第一行下面所有 n−1n-1n−1 行。因此,需要 n(n−1)=n2−nn(n-1)=n^2-nn(n−1)=n2−n 次运算,这样就使得第一个主元下方的元素均为零。检验:除了第一行的 nnn 个元素,所有的元素 n2n^2n2 个均有变化。
当消元进行到第 kkk 行时,行会变短,此时只需要 k2−kk^2-kk2−k(不是 n2−nn^2-nn2−n)次运算就可以将该列主元下方的所有元素变成零,对于 1≤k≤n1\le k\le n1≤k≤n 均成立。最后一步不需要运算,因为 12−1=01^2-1=012−1=0. 至此,向下消元就完成了,得到矩阵 UUU 共需要的计算次数是 kkk 从 111 到 nnn 所有 k2−kk^2-kk2−k 的总和:(12+22+⋯+n2)−(1+2+⋯+n)=n(n+1)(2n+1)6−n(n+1)2=n3−n3(1^2+2^2+\cdots+n^2)-(1+2+\cdots+n)=\dfrac{n(n+1)(2n+1)}{6}-\dfrac{n(n+1)}{2}=\color{blue}\dfrac{n^3-n}{3}(12+22+⋯+n2)−(1+2+⋯+n)=6n(n+1)(2n+1)−2n(n+1)=3n3−n上式利用了前 nnn 个正整数和它们平方的求和公式。将 n=100n=100n=100 代入得到一百万减去一百后再除以 333,一台工作站上执行这些操作大约要花费 1 s1\,\textrm s1s. 当 nnn 比较大时,相比于 n3n^3n3,可以忽略掉 nnn,此时可以得出主要结论:对于向下消元(A 到 U,会产生 L),乘−减操作共需要 13n3 次.\pmb{对于向下消元(A\,到\,U,会产生\,L),乘-减操作共需要\,\dfrac{1}{3}n^3\,次.}对于向下消元(A到U,会产生L),乘−减操作共需要31n3次.这表明向下消元共需要 13n3\dfrac{1}{3}n^331n3 次乘法和减法。由于 nnn 是三次方,所以 nnn 如果翻倍,那么总的运算量会变为原来的 888 倍。100100100 个方程可能还比较容易,100010001000 个的花费就会相当高,而 100001000010000 个方程几乎不可能。我们需要更快的计算机或者系数矩阵中有大量的零元素或者一个新的思想。
对于方程的右侧,计算会快很多,因为处理的是单个数,而不是整行。右端项需要 n2\pmb{n^2}n2 次运算 。向下代入 Lc=bL\boldsymbol c=\boldsymbol bLc=b 和向上回代 Ux=cU\boldsymbol x=\boldsymbol cUx=c,我们仅需要求解两个系数矩阵为三角形矩阵的方程组。在向上回代过程中,最后一个未知数只需要使用最后一个主元做一次除法,而倒数第二个方程需要两次运算 ------ 代入 xnx_nxn 然后右侧项减去前面的结果,并除以该行的主元。第 kkk 步需要 kkk 次乘 - 减运算,向上回代的总运算次数是1+2+⋯+n=n(n+1)2≈12n2次操作1+2+\cdots+n=\dfrac{n(n+1)}{2}\approx\dfrac{1}{2}n^2\kern 15pt次操作1+2+⋯+n=2n(n+1)≈21n2次操作向下代入的部分是相似的,这两个步骤总共需要 n2n^2n2 次运算,正好等于求 A−1bA^{-1}\boldsymbol bA−1b 的计算量!综上可知:高斯消元法(Gaussian elimination)相比于计算 A−1bA^{-1}\boldsymbol bA−1b 共有两大优势:
1、消元过程需要 13n3 \,\dfrac{1}{3}n^3\,31n3 次乘 - 减运算,而计算 A−1A^{-1}A−1 需要 n3 n^3\,n3 次。
2、如果 AAA 是带状矩阵,那么 LLL 和 UUU 也是:而 A−1A^{-1}A−1 通常是稠密矩阵。
五、带状矩阵
如果矩阵 AAA 有 "优质零元素" 的话,计算次数能够显著减少。优质零元素就是从 AAA 消元得到 LLL 和 UUU 的过程中,它所在的位置仍然为零。最佳的零元素是在一行的开头 ,此时这一行就不需要消元,因为乘数为零,所以它对应矩阵 LLL 的位置仍然为零。对于三对角矩阵(tridiagonal matrix)AAA (还有 Figure 11.1 中的带状矩阵)这种特征尤为明显:三对角矩阵=(两对角矩阵)×(两对角矩阵)Tridiagonal=Bidiagonal× Bidiagonal[1−1−12−1−12−1−12]=[1−11−11−11][1−11−11−11]{\color{blue}三对角矩阵=(两对角矩阵)×(两对角矩阵)}\\{\color{blue}\textrm{Tridiagonal\kern 7pt=\kern 7ptBidiagonal\kern 7pt}\times\,\textrm{Bidiagonal}}\\[1ex]\begin{bmatrix}\kern 7pt1&-1\\-1&\kern 7pt2&-1\\&-1&\kern 7pt2&-1\\&&-1&\kern 7pt2\end{bmatrix}=\begin{bmatrix}\kern 7pt1\\-1&\kern 7pt1\\&-1&\kern 7pt1\\&&-1&1\end{bmatrix}\begin{bmatrix}1&-1\\&\kern 7pt1&-1\\&&\kern 7pt1&-1\\&&&\kern 7pt1\end{bmatrix}三对角矩阵=(两对角矩阵)×(两对角矩阵)Tridiagonal=Bidiagonal×Bidiagonal 1−1−12−1−12−1−12 = 1−11−11−11 1−11−11−11 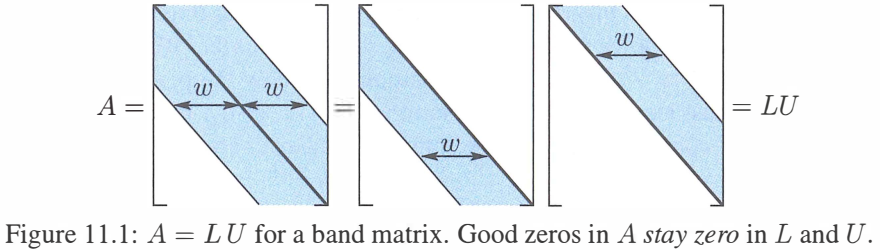
这些零元素将会使得运算次数发生巨大变化,对于 "半带宽 half-bandwidth" www:带状矩阵 band matrix A 满足当 ∣i−j∣>w 时,aij=0.\color{blue}带状矩阵\,\textrm{band matrix}\,A\,满足当\,|i-j|>w\,时,a_{ij}=0.带状矩阵band matrixA满足当∣i−j∣>w时,aij=0.当 w=1w=1w=1 时是对角矩阵,w=2w=2w=2 时是三对角矩阵,w=nw=nw=n 时是稠密矩阵。消元时,主元行需要进行运算的非零元的个数最多为 www 个,而任意主元下方的非零元素不超过 w−1w-1w−1,因此每步消元需要 w(w−1)w(w-1)w(w−1) 次运算,而带状结构仍然保留,总共有 nnn 列需要进行消元。因此:带状矩阵的消元(将 A 分解成 L 和 U)需要的运算次数少于 w2n.\color{blue}带状矩阵的消元(将\,A\,分解成\,L\,和\,U)需要的运算次数少于\,w^2n.带状矩阵的消元(将A分解成L和U)需要的运算次数少于w2n.对于带状矩阵,运算次数与阶数 nnn 成正比,而不是 n3n^3n3 了,同时也正比于 w2w^2w2. 对于稠密矩阵 w=nw=nw=n,运算次数又会回到 n3n^3n3 的数量级。计算准确的运算次数时,要记得矩阵右下角的半带宽是小于 www 的(没有足够的空间):带状矩阵w(w−1)(3n−2w+1)3稠密矩阵n(n−1)(n+1)3=n3−n3\pmb{带状矩阵}\kern 8pt\dfrac{w(w-1)(3n-2w+1)}{3}\kern 16pt\pmb{稠密矩阵}\kern 8pt\dfrac{n(n-1)(n+1)}{3}=\dfrac{n^3-n}{3}带状矩阵3w(w−1)(3n−2w+1)稠密矩阵3n(n−1)(n+1)=3n3−n在 Ax=bA\boldsymbol x=\boldsymbol bAx=b 的右侧,需要从 b\boldsymbol bb 求得 x\boldsymbol xx,运算次数大约是 2wn2wn2wn 次(稠密矩阵需要 n2n^2n2 次)。重点:对于带状矩阵,运算次数正比于 n\pmb nn , 这种消元非常迅速。对于一个 10 00010\,00010000 阶的三对角矩阵也不会有太多运算,我们并不需要计算逆矩阵 A−1A^{-1}A−1. 看下面这个带状矩阵,它的逆矩阵完全没有零元素:A=[1−100−12−100−12−100−12]有A−1=U−1L−1=[4321332122211111]A=\begin{bmatrix}\kern 7pt1&-1&\kern 7pt0&\kern 7pt0\\-1&\kern 7pt2&-1&\kern 7pt0\\\kern 7pt0&-1&\kern 7pt2&-1\\\kern 7pt0&\kern 7pt0&-1&\kern 7pt2\end{bmatrix}\kern 19pt有\kern 10ptA^{-1}=U^{-1}L^{-1}=\begin{bmatrix}4&3&2&1\\3&3&2&1\\2&2&2&1\\1&1&1&1\end{bmatrix}A= 1−100−12−100−12−100−12 有A−1=U−1L−1= 4321332122211111 实际上,已知 A−1A^{-1}A−1 要比已知 LLL 和 UUU 更麻烦。计算乘法 A−1bA^{-1}\boldsymbol bA−1b 需要 n2n^2n2 步,而求解 Lc=bL\boldsymbol c=\boldsymbol bLc=b 和 Ux=cU\boldsymbol x=\boldsymbol cUx=c 只需要 2wn2wn2wn 步。
实际问题中带状矩阵很常见,比如我们用矩阵来反映相邻数字间的关系时:由于 111 与 333 和 444 都不相邻,所以 a13=0a_{13}=0a13=0 且 a14=0a_{14}=0a14=0.
我们再讨论一下高斯 - 若尔当消元法和格拉姆 - 施密特 - 豪斯霍尔德(Gram-Schmidt-Householder)方法的计算量:
A−1 需要 n3 次 乘−减步骤QR 需要 23n3 次步骤{\color{blue}A^{-1}\,需要\,n^3\,次\,乘 - 减步骤}\kern 20pt\color{blue}QR\,需要\,\dfrac{2}{3}n^3\,次步骤A−1需要n3次乘−减步骤QR需要32n3次步骤
由于 AA−1=IAA^{-1}=IAA−1=I,所以我们可以通过 Axj=Ij(表示 I 的第 j 列)A\boldsymbol x_j=I_j(表示\,I\,的第\,j\,列)Axj=Ij(表示I的第j列) 来求解 A−1A^{-1}A−1 的第 jjj 列。左边的消元的运算量是 13n3\dfrac{1}{3}n^331n3(这个是一次性的成本!因为 LLL 和 UUU 不需要重复计算。)而 III 的第 jjj 列的前 j−1j-1j−1 个元素都为零,这就为向下代入节省了计算量。在右侧,在向下代入工作进行到第 jjj 行之前,我们不需要做任何运算,向下代入的运算量就变为了 12(n−j)2\dfrac{1}{2}(n-j)^221(n−j)2 而不再是 12n2\frac{1}{2}n^221n2 了,在这里我们忽略了低阶项,实际应为 12(n−j)(n−j+1)\dfrac{1}{2}(n-j)(n-j+1)21(n−j)(n−j+1)。由于是 nnn 阶矩阵,我们对 jjj 从 111 到 nnn 对上式求和,可以得到向下代入的总的计算量为 16n3\dfrac{1}{6}n^361n3;而向上回代并不会减少计算量,仍然为 12n3\dfrac{1}{2}n^321n3,需要注意向上回代是从下面往上回代的,所以前面的零元素并不会减少计算量。所以,求逆矩阵 A−1A^{-1}A−1 最终的乘 - 减操作的运算量为 n3n^3n3:求 A−1 的运算量:n33(求 L 和 U)+n36(向下代入)+n(n22)(向上回代)=n3(11.1.1)\pmb{求\,A^{-1}\,的运算量:}\kern 15pt\dfrac{n^3}{3}(求\,L\,和\,U)+\dfrac{n^3}{6}(向下代入)+n\Big(\dfrac{n^2}{2}\Big)(向上回代)=\pmb{n^3}\kern 20pt(11.1.1)求A−1的运算量:3n3(求L和U)+6n3(向下代入)+n(2n2)(向上回代)=n3(11.1.1)正交化(AAA 到 QQQ): 正交化与消元的主要区别是每一个乘数都是由点积决定的,这需要 nnn 次运算,而消元法只需要除以主元。4.4 节有正交化的介绍,我们进行到第 kkk 列时,需要第 kkk 列一次减去该列沿着第 j(j<k)j(j<k)j(j<k) 列的投影(jjj 是从 111 到 k−1k-1k−1),总共有 nnn 次乘 - 减运算。结合起来的运算量就是 2n2n2n,而消元法是 nnn 次。这个因数 222 就是正交化的代价。正交化过程是将点积变为零,而消元法是将非零元素变为零。
注意: 要判断一个数值算法的好坏,仅仅是看运算次数并不够 ,除了 "浮点运算次数(flop counting\textrm {flop\,counting}flopcounting)" 外,还需要研究数值的稳定性(这里豪斯霍尔德方法更好)和数据流传输。
六、稀疏矩阵的重新排列
对于固定半带宽 www 的带状矩阵,行排序是最优的。但是实际计算中的大多数稀疏矩阵(sparse matrices),带宽并不是常数,带内有很多零元。这些零元在消元过程中很可能变成非零元。我们需要对方程重新排序减少这些零元变成非零元的次数 ,这将会加快消元的速度。
一般来说,我们希望将零元移动到消元的前期所操作的行和列中,因为后期所操作的行和列会逐渐变短。MATLAB 中对稀疏矩阵重新排列的算法 "近似最小度(approximate minimum degree\textrm{\pmb approximate \pmb minimum \pmb degree}approximate minimum degree,简记为 amd\pmb{\textrm{amd}}amd)" 是贪心(greedy)算法 ------ 它不计后果的选择一个消元行,这样可能会在最后得到一个几乎稠密的(右下角)子矩阵,但是得到 LULULU 总的运算次数仍然会少很多。要使得 LLL 和 UUU 中的非零元绝对最少是一个困难的 NP\textrm{NP}NP 问题,这个代价太大,而 amd\pmb{\textrm{amd}}amd 是一个很好的折中方案。
当考虑方形网格上的每个节点与它相邻的四个点所得关联矩阵时,对其使用消元法总会将零元变为非零元,此时不可能对所有网格点进行编号并且使得其相邻节点的编号连在一起。如果我们按网格的行进行编号,那么将需要很长时间才能处理对角线上方的网格点。
在研究这种零元变为非零元的现象时,我们只需要非零元的位置信息,而并不需要它确切的值。考虑上图中非零元:aij≠0a_{ij}\neq0aij=0 表示节点 iii 和节点 jjj 相连。注意,消元法会产生非零元(新边),这也是要克服的问题。
MATLAB 中的命令 nnz(L)\textrm{\pmb{nnz}}(L)nnz(L) 会得到下三角矩阵 LLL 中非零元的数量,find(L)\textrm{\pmb{find}}(L)find(L) 会列出这些非零元,spy(L)\textrm{\pmb{spy}}(L)spy(L) 会画出这些元素的分布情况。
命令 colamd\textrm{\pmb{colamd}}colamd 和 symamd\textrm{\pmb{symamd}}symamd 的目标都是获得更好的行排序(使用对应的置换矩阵 PPP),通过选择下方具有最少非零元所在行的主元使得对 APAPAP 和 PTAPP^TAPPTAP 消元时,来减少零元变为非零元的次数。
七、快速正交化
有三种方法可以得到这个重要的矩阵分解 A=QRA=QRA=QR. 格拉姆 - 施密特 Gram-Schmidt\textrm{Gram-Schmidt}Gram-Schmidt 正交化方法可以求得 QQQ 的正交向量,按照这个方法的步骤保证了 RRR 是上三角矩阵。下面介绍两个更好的方法(豪斯霍尔德 Householder\textrm{Householder}Householder 和吉文斯 Givens\textrm{Givens}Givens 方法),它们都使用了一系列特殊的简单正交矩阵 QQQ 的乘积 ------ 也是正交矩阵。
消元法可以得到 A=LUA=LUA=LU,正交化可以得到 A=QRA=QRA=QR,现在我们不需要三角矩阵 LLL,我们需要一个正交矩阵 QQQ. LLL 是由消元矩阵 EEE 的乘积得到的,它对角线的元素全为 111,对角线下的元素是乘数 lijl_{ij}lij,QQQ 也可以由一系列正交矩阵的乘积得到。
有两种简单的正交矩阵都可以替代消元矩阵 EEE:反射矩阵 I−2uuT\pmb{I-2\boldsymbol u\boldsymbol u^T}I−2uuT,也称为豪斯霍尔德矩阵;平面旋转矩阵 ,也称为吉文斯矩阵。
下面先介绍吉文斯矩阵,下例简单的矩阵 Q21Q_{21}Q21 将 xyxyxy 平面逆时针旋转 θ\thetaθ:在平面上的吉文斯旋转Q21=[cosθ−sinθ0sinθcosθ0001]\begin{array}{}\pmb{在平面上的}\\\pmb{吉文斯旋转}\end{array}\kern 15ptQ_{21}=\begin{bmatrix}\cos\theta&-\sin\theta&0\\\sin\theta&\kern 7pt\cos\theta&0\\0&0&1\end{bmatrix}在平面上的吉文斯旋转Q21= cosθsinθ0−sinθcosθ0001 我们和用消元矩阵 E21E_{21}E21 同样的方法来使用 Q21Q_{21}Q21,选择合适的角度 θ\thetaθ,就可以将 (2,1)(2,1)(2,1) 位置上的元素变为零:Q21A=[0.60.80−0.80.60001][90−153114120−79−223200−40395]=[150−155−110075−225200−40395]Q_{21}A=\begin{bmatrix}\kern 7pt0.6&0.8&0\\\color{blue}-0.8&\color{blue}0.6&0\\\kern 7pt0&0&1\end{bmatrix}\begin{bmatrix}\color{blue}90&-153&\kern 7pt114\\\color{bllue}120&-79&-223\\200&-40&\kern 7pt395\end{bmatrix}=\begin{bmatrix}150&-155&-110\\\color{blue}0&\kern 7pt75&-225\\200&-40&\kern 7pt395\end{bmatrix}Q21A= 0.6−0.800.80.60001 90120200−153−79−40114−223395 = 1500200−15575−40−110−225395 这个零元素来自于 −0.8×90+0.6×120=0-0.8\times90+0.6\times120=0−0.8×90+0.6×120=0,我们不需要求得 θ\thetaθ,需要的是 cosθ\cos\thetacosθ 和 sinθ\sin\thetasinθ:cosθ=90902+1202,sinθ=−120902+1202(11.1.2)\cos\theta=\dfrac{90}{\sqrt{90^2+120^2}},\kern 20pt\sin\theta=\dfrac{-120}{\sqrt{90^2+120^2}}\kern 20pt(11.1.2)cosθ=902+1202 90,sinθ=902+1202 −120(11.1.2)现在我们来消去 (3,1)(3,1)(3,1) 位置处的元素,此时的旋转变换会体现在第 3,13,13,1 行和第 3,13,13,1 列的元素中,cosθ\cos\thetacosθ 和 sinθ\sin\thetasinθ 现在由 150150150 和 200200200 来确定,不再是刚才的 909090 和 120120120 了。Q31Q21A=[0.600.8010−0.800.6][150−155−110075−225200−40395]=[250−125250075−2250100325]Q_{31}Q_{21}A=\begin{bmatrix}0.6&0&0.8\\0&1&0\\\color{blue}-0.8&0&\color{blue}0.6\end{bmatrix}\begin{bmatrix}\color{blue}{150}&-155&-110\\0&\kern 7pt75&-225\\\color{blue}200&-40&\kern 7pt395\end{bmatrix}=\begin{bmatrix}250&-125&\kern 7pt250\\0&\kern 7pt75&-225\\\color{blue}0&\kern 7pt100&\kern 7pt325\end{bmatrix}Q31Q21A= 0.60−0.80100.800.6 1500200−15575−40−110−225395 = 25000−12575100250−225325 还有一步就可以得到 RRR,我们要消去 (3,2)(3,2)(3,2) 位置处的元素。现在的 cosθ\cos\thetacosθ 和 sinθ\sin\thetasinθ 由 757575 和 100100100 来确定,旋转体现在第 3,23,23,2 行和第 3,23,23,2 列中的元素中:Q32Q31Q21A=[10000.60.80−0.80.6][250−125250075−2250100325]=[250−125250012512500375]Q_{32}Q_{31}Q_{21}A=\begin{bmatrix}1&\kern 7pt0&0\\0&\kern 7pt0.6&0.8\\0&\color{blue}-0.8&\color{blue}0.6\end{bmatrix}\begin{bmatrix}250&-125&\kern 7pt250\\0&\color{blue}\kern 7pt75&-225\\0&\kern 7pt\color{blue}100&\kern 7pt325\end{bmatrix}=\begin{bmatrix}250&-125&250\\0&\kern 7pt125&125\\0&\kern 7pt\color{blue}0&375\end{bmatrix}Q32Q31Q21A= 10000.6−0.800.80.6 25000−12575100250−225325 = 25000−1251250250125375 此时我们就得到了上三角矩阵 RRR,那么 QQQ 是什么呢?将平面旋转矩阵 QijQ_{ij}Qij 移动到另一侧,就可以得到 A=QRA=QRA=QR,这里就像我们将消元矩阵 EijE_{ij}Eij 移动到另一侧得到 A=LUA=LUA=LU 一样:Q32Q31Q21A=R即A=(Q21−1Q31−1Q32−1)R=QR(11.1.3)Q_{32}Q_{31}Q_{21}A=R\kern 18pt即\kern 18ptA=(Q_{21}^{-1}Q_{31}^{-1}Q_{32}^{-1})R=QR\kern 20pt(11.1.3)Q32Q31Q21A=R即A=(Q21−1Q31−1Q32−1)R=QR(11.1.3)QijQ_{ij}Qij 的逆矩阵是 QijTQ_{ij}^{T}QijT(逆时针旋转 −θ-\theta−θ),也是一个正交矩阵,而 EijE_{ij}Eij 的逆矩阵并不是一个正交矩阵!LULULU 和 QRQRQR 形式相似,但是 LLL 和 QQQ 并不一样,它们性质不同。
下面再看一下豪斯霍尔德矩阵,它比旋转更快,因为每次回消去对角线下的整列元素。观察一下 AAA 的第一列 a1\boldsymbol a_1a1 是如何变为 RRR 的列 r1\boldsymbol r_1r1 的:
反射矩阵 H1H1=I−2uuTH1a1=[∣∣a1∣∣0⋮0]或[−∣∣a1∣∣0⋮0]=r1(11.1.4)\begin{array}{l}\pmb{反射矩阵} \,H_1\\\color{blue}H_1=I-2\boldsymbol u\boldsymbol u^T\end{array}\kern 15pt{\color{blue}H_1\boldsymbol a_1}=\begin{bmatrix}||\boldsymbol a_1||\\0\\\vdots\\0\end{bmatrix}\kern 5pt或\kern 5pt\begin{bmatrix}-||\boldsymbol a_1||\\0\\\vdots\\0\end{bmatrix}={\color{blue}\boldsymbol r_1}\kern 15pt(11.1.4)反射矩阵H1H1=I−2uuTH1a1= ∣∣a1∣∣0⋮0 或 −∣∣a1∣∣0⋮0 =r1(11.1.4)
变换后长度不变,单位向量 u1\boldsymbol u_1u1 和 a1−r1\boldsymbol a_1-\boldsymbol r_1a1−r1 方向相同,这样就可以求得 u1\boldsymbol u_1u1。我们利用单位向量 u1\boldsymbol u_1u1 中的 n−1n-1n−1 个元素来得到 r1\boldsymbol r_1r1 中的 n−1n-1n−1 个零元素,而吉文斯方法旋转一个角度 θ\thetaθ 只能得到一个零元素。当我们进行到第 kkk 列时,uk\boldsymbol u_kuk 中会有 n−kn-kn−k 个可选的元素,它们用来得到 rk\boldsymbol r_krk 中的 n−kn-kn−k 个零。我们只需要存储每个 u\boldsymbol uu 和 r\boldsymbol rr 就可以得到最终的 QQQ 和 RRR:Hi 的逆矩阵仍是 Hi(Hn−1Hn−2⋯H1)A=R即A=(H1H2⋯Hn−1)R=QR(11.1.5)H_i\,\pmb{的逆矩阵仍是}\,H_i\kern 12pt(H_{n-1}H_{n-2}\cdots H_1)A=R\kern 10pt即\kern 10ptA=(H_1H_2\cdots H_{n-1})R=QR\kern 12pt(11.1.5)Hi的逆矩阵仍是Hi(Hn−1Hn−2⋯H1)A=R即A=(H1H2⋯Hn−1)R=QR(11.1.5)这是 LAPACK\textrm{LAPACK}LAPACK 软件在 191919 世纪用于改善 Gram-Schmidt\textrm{Gram-Schmidt}Gram-Schmidt 方法的成果,QQQ 的确是一个正交矩阵。
A=QRA=QRA=QR 分解还会应用在另一个大规模数值线性代数问题上------ 特征值问题 。它的基本思想是:将分解式 QRQRQR 颠倒得到 A1=QRA_1=QRA1=QR,这个就是 Q−1AQQ^{-1}AQQ−1AQ,由于 A1A_1A1 和 AAA 相似,所以它们有相同的特征值;再将 A1A_1A1 分解为 Q1R1Q_1R_1Q1R1,然后颠倒分解式得到 A2=R1Q1A_2=R_1Q_1A2=R1Q1,依次进行下去,将会惊奇的发现 A1,A2,A3,⋯A_1,A_2,A_3,\cdotsA1,A2,A3,⋯ 对角线下方元素的绝对值会越来越小,我们可以由此确定特征值。这个就是求解 Ax=λxA\boldsymbol x=\lambda\boldsymbol xAx=λx 的 "QRQRQR 方法",是数值线性代数的一次大成功。