目录
[1. Queue 是什么?](#1. Queue 是什么?)
[2. Queue 的继承体系](#2. Queue 的继承体系)
[1.Queue 的核心操作方法(最关键的部分)](#1.Queue 的核心操作方法(最关键的部分))
[2. 常见的 Queue 实现类](#2. 常见的 Queue 实现类)
[1. 顺序队列的表示](#1. 顺序队列的表示)
[2. 顺序队列的假溢出](#2. 顺序队列的假溢出)
[3. 顺序循环队列](#3. 顺序循环队列)
前言
队列(Queue)作为计算机科学中最重要的数据结构之一,是每一个程序员必须掌握的基础知识。无论是在操作系统中的进程调度、网络数据包的处理,还是日常开发中的任务管理,队列都扮演着不可或缺的角色。本文将从队列的基本概念出发,深入剖析Java集合框架中的队列接口及其实现,详细讲解顺序队列、链式队列等不同实现方式的原理与特点,并通过杨辉三角等实际案例展示队列的典型应用。无论你是刚入门的编程新手,还是希望巩固数据结构知识的开发者,相信本文都能为你提供有价值的参考和启发。
正文
一、队列(Queue)的定义
1. Queue 是什么?
Queue(队列)是 Java 集合框架(Java Collections Framework)中的一个重要接口,它位于 java.util包下。它专门用于在处理之前保存元素。
队列的核心特性是遵循 **FIFO(First-In-First-Out,先进先出)** 原则。你可以把它想象成现实生活中的排队:先来的人先接受服务。
重要提示 : 虽然 FIFO 是最常见的规则,但并非所有 Queue的实现都严格遵守。例如,PriorityQueue会根据元素的优先级进行排序,而不是插入顺序。
2. Queue 的继承体系
java
java.util.Collection
↑
java.util.Queue
↑
java.util.Deque (子接口,代表双端队列)Queue接口直接继承自 Collection接口,这意味着所有集合的基本操作(如 add, remove, size, isEmpty等)它都拥有。Deque是 Queue的子接口,提供了在两端进行操作的能力。
二、java.util包中的队列接口
1.Queue 的核心操作方法(最关键的部分)
Queue接口为基本操作(插入、移除、检查)各提供了两种形式的方法。这两种形式的行为在遇到异常情况(如空队列或容量限制)时完全不同。这是学习 Queue的重中之重。
| 操作类型 | 抛出异常的方法 | 返回特殊值的方法 | 说明 |
|---|---|---|---|
| **插入(Insert)** | boolean add(E e) |
boolean offer(E e) |
向队列尾部插入一个元素。 |
| **移除(Remove)** | E remove() |
E poll() |
获取并移除队列头部的元素。 |
| **检查(Examine)** | E element() |
E peek() |
获取但不移除队列头部的元素。 |
两种方法的区别:
-
抛出异常组(Throws exception):
-
如果操作失败(例如,向一个已满的队列
add,或从一个空队列remove),这些方法会立即抛出异常(通常是IllegalStateException或NoSuchElementException)。 -
适用于你确信操作会成功的场景。
-
-
返回特殊值组(Returns special value):
-
如果操作失败,这些方法不会抛出异常,而是返回一个特殊值(
false或null)。 -
适用于在容量受限的队列中,或者需要优雅处理失败情况的场景(例如,多线程环境)。
-
简单记忆 :带有 offer, poll, peek的方法更"友好",因为它们用返回值代替了异常。
2. 常见的 Queue 实现类
Queue是一个接口,你需要使用它的实现类。以下是 java.util包中几个最重要的实现:
1.LinkedList
最常用的通用队列实现。
它实现了 List接口,也实现了 Queue接口。
它没有容量限制(除非内存耗尽)。
基于链表实现。
注意 :LinkedList也实现了 Deque接口,所以它可以作为双端队列使用。
java
Queue<String> queue = new LinkedList<>();
queue.offer("A");
queue.offer("B");
String first = queue.poll(); // 返回 "A"2.PriorityQueue
不遵循 FIFO。
元素根据其自然顺序 (例如,数字从小到大,字符串按字典序)或通过构造时提供的 **Comparator** 进行排序。
出队(poll)时,总是返回当前队列中优先级最高的元素。
它没有容量限制。
内部基于堆(Heap)数据结构实现。
java
// 自然顺序(从小到大)
Queue<Integer> priorityQueue = new PriorityQueue<>();
priorityQueue.offer(5);
priorityQueue.offer(1);
priorityQueue.offer(3);
while (!priorityQueue.isEmpty()) {
System.out.println(priorityQueue.poll()); // 输出顺序:1, 3, 5
}3.ArrayDeque
一个基于可调整大小数组实现的双端队列。
作为队列使用时,性能通常比 LinkedList更好。
没有容量限制。
它不能存储 null元素。
通常作为栈(Stack)或双端队列(Deque)使用时的首选
java
Queue<String> queue = new ArrayDeque<>();
queue.offer("X");
queue.offer("Y");
String next = queue.poll(); // 返回 "X"3.线程安全的队列
在这里,先给大家画个饼,关于线程,我们等到以后开线程专栏再讲,这里只做提及,让大家记得有这个东西。包括在接口中讲的数据库,也是会开专栏的。顺带提一嘴,我们在半小时漫画计算机中很早就提及过线程,在不同的地方遇到这些东西的时候就会有一种城市羡慕连接的感觉。
4.使用示例
java
import java.util.LinkedList;
import java.util.Queue;
public class QueueExample {
public static void main(String[] args) {
// 1. 创建一个队列(使用 LinkedList 实现)
Queue<String> waitingQueue = new LinkedList<>();
// 2. 向队列添加元素 (推荐使用 offer)
waitingQueue.offer("张三");
waitingQueue.offer("李四");
waitingQueue.offer("王五");
waitingQueue.add("赵六"); // 也可以用 add
System.out.println("等待队列: " + waitingQueue); // 输出: [张三, 李四, 王五, 赵六]
// 3. 查看队列头部的元素(不移除)
String firstPerson = waitingQueue.peek();
System.out.println("正在服务: " + firstPerson); // 输出: 张三
System.out.println("当前队列: " + waitingQueue); // 队列不变
// 4. 移除并返回队列头部的元素(服务完毕)
String servedPerson = waitingQueue.poll();
System.out.println("已服务: " + servedPerson); // 输出: 张三
System.out.println("剩余队列: " + waitingQueue); // 输出: [李四, 王五, 赵六]
// 5. 循环处理队列中的所有元素
System.out.println("开始服务剩余顾客:");
while (!waitingQueue.isEmpty()) {
String person = waitingQueue.poll();
System.out.println(" - 正在服务: " + person);
}
System.out.println("最终队列为空: " + waitingQueue.isEmpty()); // 输出: true
// 6. 尝试从空队列中 poll 和 remove
System.out.println("从空队列poll: " + waitingQueue.poll()); // 输出: null (友好)
// String result = waitingQueue.remove(); // 这行会抛出 NoSuchElementException 异常
}
}三、顺序队列
1. 顺序队列的表示
顺序队列使用数组作为底层存储结构,通过两个指针front和rear来分别指向队头和队尾
java
public class SqQueue<T> {
final int QUEUESIZE = 20;
T s[];
int front, rear;
SqQueue() {
front = 0;
rear = 0;
s = (T[]) new Object[QUEUESIZE];
}
// 判断队列是否为空
public boolean isEmpty() {
return front == rear;
}
// 判断队列是否已满
public boolean isFull() {
return (rear + 1) % QUEUESIZE == front;
}
// 入队操作
public boolean offer(T item) {
if (isFull()) {
return false; // 队列已满
}
s[rear] = item;
rear = (rear + 1) % QUEUESIZE;
return true;
}
// 出队操作
public T poll() {
if (isEmpty()) {
return null;
}
T item = s[front];
front = (front + 1) % QUEUESIZE;
return item;
}
// 获取队头元素
public T peek() {
if (isEmpty()) {
return null;
}
return s[front];
}
}2. 顺序队列的假溢出
问题描述:
假溢出是指队列的存储空间实际上还有空闲位置,但由于队列的线性存储结构导致无法继续插入新元素的现象。
产生原因:
在普通顺序队列中,元素入队时rear指针后移,出队时front指针后移
当rear指针到达数组末尾时,即使数组前面有空闲位置(已出队的元素位置),也无法继续插入新元素
这造成了存储空间的浪费
java
初始状态:front=0, rear=0
[null][null][null][null][null]
执行入队A,B,C:front=0, rear=3
[A][B][C][null][null]
执行出队A:front=1, rear=3
[已出队][B][C][null][null]
此时虽然数组前部有空位,但rear=3已到末尾,无法继续插入新元素 → 假溢出3. 顺序循环队列
为了解决假溢出问题,我们引入循环队列的概念,将数组视为一个环状结构。
循环队列的实现要点:
-
队空条件:
front == rear -
队满条件:
(rear + 1) % QUEUESIZE == front -
入队操作:
rear = (rear + 1) % QUEUESIZE -
出队操作:
front = (front + 1) % QUEUESIZE
循环队列示例:
java
public class CircularQueue<T> {
private T[] queue;
private int front;
private int rear;
private int size;
public CircularQueue(int capacity) {
queue = (T[]) new Object[capacity];
front = 0;
rear = 0;
size = 0;
}
public boolean enqueue(T item) {
if (isFull()) return false;
queue[rear] = item;
rear = (rear + 1) % queue.length;
size++;
return true;
}
public T dequeue() {
if (isEmpty()) return null;
T item = queue[front];
front = (front + 1) % queue.length;
size--;
return item;
}
public boolean isFull() {
return size == queue.length;
}
public boolean isEmpty() {
return size == 0;
}
}四、双端队列(Deque)
双端队列(Double Ended Queue)是一种允许在两端进行插入和删除操作的特殊队列。
主要特点:
可以从队头或队尾插入元素
可以从队头或队尾删除元素
结合了栈和队列的特性
Java中的Deque接口方法:
| 操作 | 队头操作 | 队尾操作 |
|---|---|---|
| 插入 | addFirst(e) / offerFirst(e) | addLast(e) / offerLast(e) |
| 删除 | removeFirst() / pollFirst() | removeLast() / pollLast() |
| 查看 | getFirst() / peekFirst() | getLast() / peekLast() |
java
Deque<String> deque = new ArrayDeque<>();
deque.offerFirst("A"); // 队头插入
deque.offerLast("B"); // 队尾插入
deque.offerLast("C");
System.out.println(deque.pollFirst()); // 输出A(队头删除)
System.out.println(deque.pollLast()); // 输出C(队尾删除)五、链式队列
链式队列使用链表作为存储结构,克服了顺序队列的固定容量限制。
链式队列的实现
java
public class LinkedQueue<T> {
private QueueNode<T> front; // 队头指针
private QueueNode<T> rear; // 队尾指针
private int size;
public LinkedQueue() {
front = rear = null;
size = 0;
}
// 入队操作
public boolean offer(T data) {
QueueNode<T> newNode = new QueueNode<>(data);
if (rear == null) {
// 空队列情况
front = rear = newNode;
} else {
rear.next = newNode;
rear = newNode;
}
size++;
return true;
}
// 出队操作
public T poll() {
if (front == null) {
return null;
}
T data = front.data;
front = front.next;
if (front == null) {
rear = null; // 队列变空,重置rear
}
size--;
return data;
}
// 获取队头元素
public T peek() {
return front == null ? null : front.data;
}
public boolean isEmpty() {
return front == null;
}
public int size() {
return size;
}
}
class QueueNode<T> {
T data;
QueueNode<T> next;
public QueueNode(T data) {
this.data = data;
this.next = null;
}
}链式队列的特点
优点:
动态分配内存,无需担心容量限制
插入删除操作的时间复杂度为O(1)
不会出现假溢出问题
缺点:
每个节点需要额外的指针空间
访问需要遍历,不能随机访问
六、对比
| 队列类型 | 存储结构 | 优点 | 缺点 | 适用场景 |
|---|---|---|---|---|
| 顺序队列 | 数组 | 内存连续,访问快 | 固定容量,假溢出 | 已知最大容量 |
| 循环队列 | 数组 | 解决假溢出问题 | 浪费一个存储单元 | 需要循环使用的场景 |
| 链式队列 | 链表 | 动态扩容,无假溢出 | 额外指针开销 | 容量不确定的场景 |
| 双端队列 | 数组/链表 | 操作灵活 | 实现相对复杂 | 需要在两端操作的场景 |
七、用队列实现杨辉三角
1.介绍
杨辉三角,又称帕斯卡三角,是二项式系数在三角形中的一种几何排列,最早可追溯至北宋时期数学家贾宪的"开方作法本源图",而南宋数学家杨辉在《详解九章算法》中详细记载并普及了此图,故在中文数学文献中常被称为"杨辉三角"。其基本规则是每个数等于它上方两数之和(即第n行的第k个数等于第n-1行的第k-1个数与第k个数之和),且每行左右对称(从中间一列开始),由1开始,顶端为第0行,每行数字从第0列开始计数。杨辉三角在组合数学、概率论、代数等领域有广泛应用,例如第n行的数字对应二项式(a+b)^n展开的系数,同时每一行的数字之和等于2的n次方等。
2.代码实现
java
import java.util.LinkedList;
import java.util.Queue;
public class YangHuiWithQueue {
public static void main(String[] args) {
printYangHuiWithQueue(10);
}
public static void printYangHuiWithQueue(int n) {
if (n <= 0) return;
Queue<Integer> queue = new LinkedList<>();
// 第一行
queue.offer(1);
System.out.println("1");
for (int i = 2; i <= n; i++) {
// 每行的第一个数字是1
int prev = 0;
int current;
// 生成当前行的数字
for (int j = 0; j < i - 1; j++) {
current = queue.poll();
// 计算当前数字:上一行的左上方数字 + 上一行的正上方数字
queue.offer(prev + current);
prev = current;
}
// 每行的最后一个数字是1
queue.offer(1);
// 打印当前行
printQueue(new LinkedList<>(queue));
}
}
private static void printQueue(Queue<Integer> queue) {
Queue<Integer> temp = new LinkedList<>(queue);
while (!temp.isEmpty()) {
System.out.print(temp.poll() + " ");
}
System.out.println();
}
}3.结果演示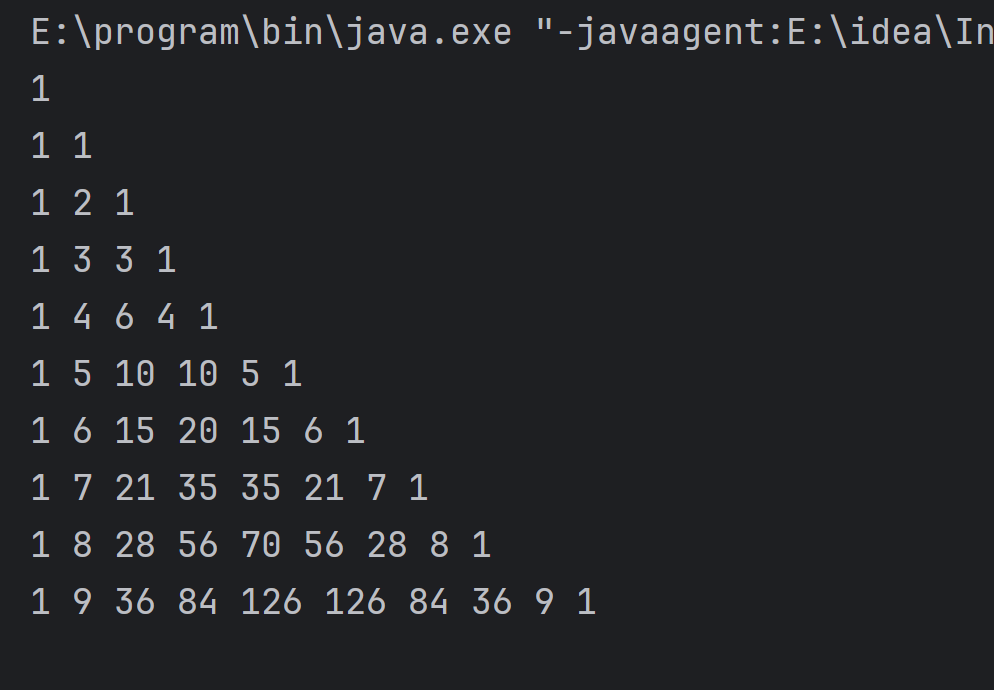
由于这里排版不是重点,且难度很低,就不进行排版了,减少操作
总结
通过本文的全面讲解,我们对队列这一重要的数据结构有了系统而深入的认识。从基础的FIFO原则到Java集合框架中Queue接口的具体实现,从顺序队列的假溢出问题到循环队列的巧妙解决方案,从链式队列的动态特性到双端队列的灵活操作,我们逐步构建了完整的队列知识体系。
队列不仅仅是数据结构课本中的一个概念,更是解决实际问题的有力工具。通过杨辉三角的实现案例,我们看到了队列在算法设计中的巧妙应用。不同的队列实现各有优劣:顺序队列适合已知容量的场景,链式队列适合动态扩容的需求,双端队列则为特殊操作提供了便利。在实际开发中,我们需要根据具体需求选择最合适的队列类型。
掌握队列的核心在于理解其"先进先出"的本质特征以及各种实现方式的内在原理。希望本文能够帮助读者建立起对队列的深刻理解,为后续学习更复杂的数据结构和算法打下坚实基础。
致谢
在本文的撰写过程中,我要感谢Java官方文档提供的准确技术规范,以及开源社区中众多开发者分享的宝贵经验。同时感谢所有数据结构领域的先驱者,他们的智慧结晶为我们今天的学习提供了丰富的理论支撑。
特别感谢CSDN平台为技术爱好者提供了如此优秀的知识分享环境,让开发者能够相互学习、共同进步。也要感谢每一位坚持阅读到这里的读者,你们的关注和认可是我持续创作的最大动力。如果本文中存在任何疏漏或不足之处,欢迎各位读者批评指正,让我们在技术道路上携手共进。
最后,希望本文能够成为读者学习队列数据结构的有益参考,期待在未来的技术文章中与大家再次相遇!