day04 小美的区间删除

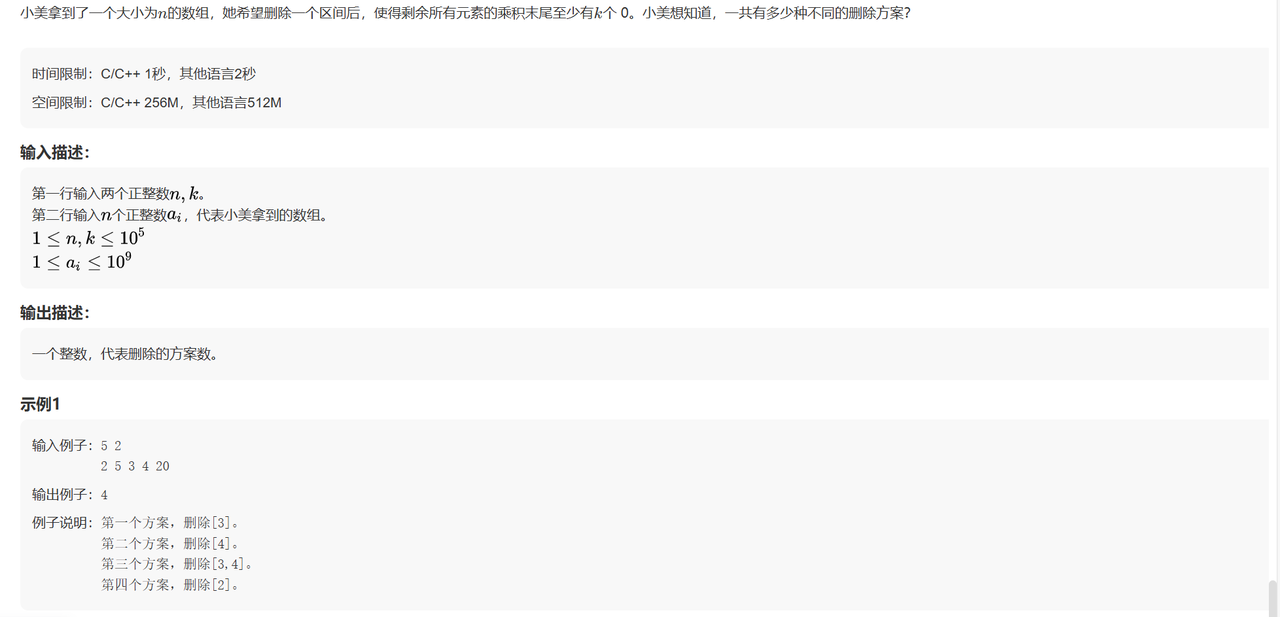
k个0，也即k个（2，5）组合，首先统计每个元素包含的 2 和 5 的个数

java 复制代码

        // 计算每个元素的2和5的个数
        int[] cnt2 = new int[n];
        int[] cnt5 = new int[n];
        for (int i = 0; i < n; i++) {
            int x = a[i];
            int c2 = 0, c5 = 0;
            while (x % 2 == 0) {
                c2++;
                x /= 2;
            }
            while (x % 5 == 0) {
                c5++;
                x /= 5;
            }
            cnt2[i] = c2;
            cnt5[i] = c5;
        }

其次，区间删除，我们可以让pre2 和 pre5 数组分别存储前 i 个元素中 2 和 5 的总个数，便于快速计算任意区间的 2 和 5 的个数。

java 复制代码

        // 计算前缀和
        long[] pre2 = new long[n + 1];
        long[] pre5 = new long[n + 1];
        for (int i = 0; i < n; i++) {
            pre2[i + 1] = pre2[i] + cnt2[i];
            pre5[i + 1] = pre5[i] + cnt5[i];
        }

排除特殊情况，不删除区间的情况下，也无法满足k个0后缀；或者k=0，所有可能的删除方案

java 复制代码

        long total2 = pre2[n];
        long total5 = pre5[n];

        // 特殊情况：总2或总5不足k，直接返回0
        if (total2 < k || total5 < k) {
            System.out.println(0);
            return;
        }

        // 特殊情况：k=0，所有可能的删除方案
        if (k == 0) {
            System.out.println((long) n * (n + 1) / 2);
            return;
        }

这里选择区间，如果暴力遍历的话，很显然会超时。我们这里可以使用双指针遍历 ：右指针 R 遍历每个可能的区间右边界，左指针 L 则根据当前区间是否满足条件进行调整。对于每个 R，找到最小的 L 使得删除区间 [L, R] 后剩余元素的 2 和 5 的个数均不小于 k，此时 [L, R] 到 [R, R] 的所有区间均为有效方案，统计其个数并累加到结果中。

java 复制代码

        long ans = 0;
        int L = 0; 
        for (int R = 0; R < n; R++) {
            while (L <= R) {
                long current2 = pre2[R + 1] - pre2[L];
                long current5 = pre5[R + 1] - pre5[L];
                if (total2 - current2 >= k && total5 - current5 >= k) {
                    break; 
                } else {
                    L++; 
                }
            }

            if (L <= R) {
                ans += (R - L + 1);
            }
        }

完整代码：

java 复制代码

import java.util.*;
import java.io.*;

public class Main {
    public static void main(String[] args) throws IOException {
        //读取输入
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] line = br.readLine().split(" ");
        int n = Integer.parseInt(line[0]);
        int k = Integer.parseInt(line[1]);
        int[] a = new int[n];
        line = br.readLine().split(" ");
        for (int i = 0; i < n; i++) {
            a[i] = Integer.parseInt(line[i]);
        }

        // 计算每个元素的2和5的个数
        int[] cnt2 = new int[n];
        int[] cnt5 = new int[n];
        for (int i = 0; i < n; i++) {
            int x = a[i];
            int c2 = 0, c5 = 0;
            while (x % 2 == 0) {
                c2++;
                x /= 2;
            }
            while (x % 5 == 0) {
                c5++;
                x /= 5;
            }
            cnt2[i] = c2;
            cnt5[i] = c5;
        }

        // 计算前缀和
        long[] pre2 = new long[n + 1];
        long[] pre5 = new long[n + 1];
        for (int i = 0; i < n; i++) {
            pre2[i + 1] = pre2[i] + cnt2[i];
            pre5[i + 1] = pre5[i] + cnt5[i];
        }

        long total2 = pre2[n];
        long total5 = pre5[n];

        // 特殊情况：总2或总5不足k，直接返回0
        if (total2 < k || total5 < k) {
            System.out.println(0);
            return;
        }

        // 特殊情况：k=0，所有可能的删除方案
        if (k == 0) {
            System.out.println((long) n * (n + 1) / 2);
            return;
        }

        long ans = 0;
        int L = 0; 
        for (int R = 0; R < n; R++) {
            while (L <= R) {
                long current2 = pre2[R + 1] - pre2[L];
                long current5 = pre5[R + 1] - pre5[L];
                if (total2 - current2 >= k && total5 - current5 >= k) {
                    break; 
                } else {
                    L++; 
                }
            }

            if (L <= R) {
                ans += (R - L + 1);
            }
        }

        System.out.println(ans);

    }
}