《统计学习方法》第4章——朴素贝叶斯法【学习笔记】

前言

学习机器学习的过程中，我逐渐意识到：
如果只有代码，而没有理论，就很难真正理解模型在做什么
如果只有概念，而缺少一个系统框架，又难以把知识串成体系

《统计学习方法》正好提供了这样一个结构清晰的入口------它把机器学习的核心思想和经典算法用统计学的语言表达出来，帮助我们理解算法背后的原理。

因此，我决定开启这个专栏，用自己的方式整理学习笔记。主要目标是：

用更直白的语言梳理书中的概念
把知识点整理成便于查阅和复习的形式
记录自己的理解和思考过程

这些笔记主要是我个人的学习记录，如果恰好对你也有帮助，那就更好了。希望通过这个过程，能让自己对机器学习的理论基础有更扎实的理解。

第4章------朴素贝叶斯法

本章叙述朴素贝叶斯法，包括朴素贝叶斯法的学习与分类、朴素贝叶斯法的参数估计算法。

4.1 朴素贝叶斯法的学习与分类

4.1.1 基本方法

问题设定

输入空间 : X⊆Rn\mathcal{X} \subseteq \mathbb{R}^nX⊆Rn 是 nnn 维向量的集合
输出空间 : Y={c1,c2,⋯ ,cK}\mathcal{Y} = \{c_1, c_2, \cdots, c_K\}Y={c1,c2,⋯,cK} 是类标记集合
训练数据集 : T={(x1,y1),(x2,y2),⋯ ,(xN,yN)}T = \{(x_1, y_1), (x_2, y_2), \cdots, (x_N, y_N)\}T={(x1,y1),(x2,y2),⋯,(xN,yN)}，由联合概率分布 P(X,Y)P(X,Y)P(X,Y) 独立同分布产生

朴素贝叶斯法通过训练数据学习联合概率分布 P(X,Y)P(X,Y)P(X,Y)，具体分为两步：

学习先验概率分布
P(Y=ck),k=1,2,⋯ ,KP(Y = c_k), \quad k = 1, 2, \cdots, K P(Y=ck),k=1,2,⋯,K
学习条件概率分布
P(X=x∣Y=ck)=P(X(1)=x(1),⋯ ,X(n)=x(n)∣Y=ck),k=1,2,⋯ ,KP(X = x | Y = c_k) = P(X^{(1)} = x^{(1)}, \cdots, X^{(n)} = x^{(n)} | Y = c_k), \quad k = 1, 2, \cdots, K P(X=x∣Y=ck)=P(X(1)=x(1),⋯,X(n)=x(n)∣Y=ck),k=1,2,⋯,K

朴素贝叶斯假设（条件独立性假设）

❓为什么需要条件独立性假设呢？

如果不使用条件独立性假设，我们需要估计完整的条件概率分布：

P(X(1)=x(1),X(2)=x(2),⋯ ,X(n)=x(n)∣Y=ck)P(X^{(1)} = x^{(1)}, X^{(2)} = x^{(2)}, \cdots, X^{(n)} = x^{(n)} | Y = c_k)P(X(1)=x(1),X(2)=x(2),⋯,X(n)=x(n)∣Y=ck)

这意味着需要估计 nnn 个特征的所有可能组合的概率。

假设我们要做垃圾邮件分类：

特征数 n=10n = 10n=10（简化的例子，实际可能有几千个特征）

每个特征的取值数 Sj=2S_j = 2Sj=2（例如：单词是否出现）

类别数 K=2K = 2K=2（垃圾邮件 vs 正常邮件）

不使用条件独立性假设

需要估计的参数数量： K×∏j=1nSj=2×210=2×1024=2048 个参数K \times \prod_{j=1}^{n} S_j = 2 \times 2^{10} = 2 \times 1024 = 2048 \text{ 个参数}K×j=1∏nSj=2×210=2×1024=2048 个参数

如果特征数增加到 n=100n = 100n=100： 2×2100=2×1.27×1030≈2.5×1030 个参数2 \times 2^{100} = 2 \times 1.27 \times 10^{30} \approx 2.5 \times 10^{30} \text{ 个参数}2×2100=2×1.27×1030≈2.5×1030 个参数

这是天文数字！即使整个互联网的数据也不够估计这么多参数。

使用条件独立性假设

需要估计的参数数量： K×∑j=1nSj=2×(2×10)=40 个参数K \times \sum_{j=1}^{n} S_j = 2 \times (2 \times 10) = 40 \text{ 个参数}K×j=1∑nSj=2×(2×10)=40 个参数

如果特征数增加到 n=100n = 100n=100： 2×(2×100)=400 个参数2 \times (2 \times 100) = 400 \text{ 个参数}2×(2×100)=400 个参数

线性增长，完全可行！

这就是为什么叫"朴素"（Naive）贝叶斯------它做了一个简单但不太现实的假设，却换来了巨大的计算优势！

朴素贝叶斯法的核心假设：给定类别 Y=ckY = c_kY=ck 的条件下，各个特征相互独立。

P(X=x∣Y=ck)=∏j=1nP(X(j)=x(j)∣Y=ck)P(X = x | Y = c_k) = \prod_{j=1}^{n} P(X^{(j)} = x^{(j)} | Y = c_k) P(X=x∣Y=ck)=j=1∏nP(X(j)=x(j)∣Y=ck)

说明: 这个假设大大简化了计算，虽然在实际中往往不成立，但朴素贝叶斯法在很多情况下仍然有效。

对于给定的输入 xxx，通过贝叶斯定理计算后验概率：

P(Y=ck∣X=x)=P(X=x∣Y=ck)P(Y=ck)∑kP(X=x∣Y=ck)P(Y=ck)P(Y = c_k | X = x) = \frac{P(X = x | Y = c_k) P(Y = c_k)}{\sum_k P(X = x | Y = c_k) P(Y = c_k)} P(Y=ck∣X=x)=∑kP(X=x∣Y=ck)P(Y=ck)P(X=x∣Y=ck)P(Y=ck)

代入条件独立性假设，得到朴素贝叶斯分类的基本公式：

P(Y=ck∣X=x)=P(Y=ck)∏jP(X(j)=x(j)∣Y=ck)∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck),k=1,2,⋯ ,KP(Y = c_k | X = x) = \frac{P(Y = c_k) \prod_j P(X^{(j)} = x^{(j)} | Y = c_k)}{\sum_k P(Y = c_k) \prod_j P(X^{(j)} = x^{(j)} | Y = c_k)}, \quad k = 1, 2, \cdots, K P(Y=ck∣X=x)=∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)P(Y=ck)∏jP(X(j)=x(j)∣Y=ck),k=1,2,⋯,K

选择后验概率最大的类作为预测结果（贝叶斯分类器）：

y=f(x)=arg⁡max⁡ckP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)y = f(x) = \arg\max_{c_k} \frac{P(Y = c_k) \prod_j P(X^{(j)} = x^{(j)} | Y = c_k)}{\sum_k P(Y = c_k) \prod_j P(X^{(j)} = x^{(j)} | Y = c_k)} y=f(x)=argckmax∑kP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)P(Y=ck)∏jP(X(j)=x(j)∣Y=ck)

由于分母对所有 ckc_kck 都相同，可以简化为：

y=arg⁡max⁡ckP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)y = \arg\max_{c_k} P(Y = c_k) \prod_j P(X^{(j)} = x^{(j)} | Y = c_k) y=argckmaxP(Y=ck)j∏P(X(j)=x(j)∣Y=ck)

4.1.2 后验概率最大化的意义

核心思想

朴素贝叶斯法为什么要选择后验概率最大 的类别？其实这背后有一个很自然的逻辑：最小化分类错误的风险。

我们定义一个简单的 0-1 损失函数：
L(Y,f(X))={1,Y≠f(X) （分类错误）,0,Y=f(X) （分类正确）. L(Y, f(X)) = \begin{cases} 1, & Y \neq f(X)\ \text{（分类错误）},\\[6pt] 0, & Y = f(X)\ \text{（分类正确）}. \end{cases} L(Y,f(X))=⎩ ⎨ ⎧1,0,Y=f(X) （分类错误）,Y=f(X) （分类正确）.

这个函数的意思很直白：分错了就损失 1，分对了损失为 0。

对于每个可能的输入 XXX，我们把所有类别的损失加权求和，权重就是该类别的后验概率：

Rexp⁡(f)=EX∑k=1K[L(ck,f(X))]P(ck∣X)R_{\exp}(f) = E_X \sum_{k=1}^{K} [L(c_k, f(X))] P(c_k | X)Rexp(f)=EXk=1∑K[L(ck,f(X))]P(ck∣X)

最小化风险

要让期望风险最小，我们只需要对每个具体的 X=xX = xX=x 单独最小化：

f(x)=arg⁡min⁡y∈Y∑k=1KL(ck,y)P(ck∣X=x)f(x) = \arg\min_{y \in \mathcal{Y}} \sum_{k=1}^{K} L(c_k, y) P(c_k | X = x)f(x)=argy∈Ymink=1∑KL(ck,y)P(ck∣X=x)

代入 0-1 损失函数：

当 y=cky = c_ky=ck 时，L(ck,y)=0L(c_k, y) = 0L(ck,y)=0
当 y≠cky \neq c_ky=ck 时，L(ck,y)=1L(c_k, y) = 1L(ck,y)=1

所以求和项变成：

f(x)=arg⁡min⁡y∈Y∑k=1KP(y≠ck∣X=x)f(x) = \arg\min_{y \in \mathcal{Y}} \sum_{k=1}^{K} P(y \neq c_k | X = x)f(x)=argy∈Ymink=1∑KP(y=ck∣X=x)

=arg⁡min⁡y∈Y(1−P(y=ck∣X=x))= \arg\min_{y \in \mathcal{Y}} (1 - P(y = c_k | X = x))=argy∈Ymin(1−P(y=ck∣X=x))

=arg⁡max⁡y∈YP(y=ck∣X=x)= \arg\max_{y \in \mathcal{Y}} P(y = c_k | X = x)=argy∈YmaxP(y=ck∣X=x)

结论

最小化期望风险 ⟺ 最大化后验概率

f(x)=arg⁡max⁡ckP(ck∣X=x)f(x) = \arg\max_{c_k} P(c_k | X = x)f(x)=argckmaxP(ck∣X=x)

这就是朴素贝叶斯法的理论依据。

对于分类任务，在已知后验概率的情况下选择概率最大 的类别，其实就是在最小化 0-1 损失的期望错误率。因为在每一次预测中，选择后验概率最高的那一类，等价于让"预测错误的概率"尽可能小；从整体来看，这种策略能保证在所有可能的分类规则中达到最低的平均错误率。

因此，即使它不能保证每次都正确，但从长期统计意义上，它是犯错最少、最合理、也是最优的选择，这就是贝叶斯最优分类器的核心思想。

4.2 朴素贝叶斯法的参数估计

4.2.1 极大似然估计

在朴素贝叶斯方法里，我们要估计两类概率：

先验概率 P(Y=ck)P(Y=c_k)P(Y=ck)
条件概率 P(X(j)=ajl∣Y=ck)P(X^{(j)} = a_{jl} \mid Y=c_k)P(X(j)=ajl∣Y=ck)

朴素贝叶斯直接用训练数据的频率来估计这两个概率，也就是用 极大似然估计（MLE）。

1. 先验概率的 MLE

含义： 某一类 ckc_kck 在训练集中出现的比例。

公式：
P(Y=ck)=1N∑i=1NI(yi=ck)P(Y=c_k)=\frac{1}{N}\sum_{i=1}^N I(y_i=c_k)P(Y=ck)=N1i=1∑NI(yi=ck)

分子：类别 ckc_kck 出现的次数
分母：总样本数 (N)

2. 条件概率的 MLE

含义： 在类别为 ckc_kck 的数据中，第 jjj 个特征取某个值 ajla_{jl}ajl 的比例。

公式：
P(X(j)=ajl∣Y=ck)∑i=1NI(xi(j)=ajl, yi=ck)∑i=1NI(yi=ck)P(X^{(j)} = a_{jl}\mid Y=c_k) \frac{\sum_{i=1}^N I(x_i^{(j)}=a_{jl},\ y_i=c_k)} {\sum_{i=1}^N I(y_i=c_k)}P(X(j)=ajl∣Y=ck)∑i=1NI(yi=ck)∑i=1NI(xi(j)=ajl, yi=ck)

分子：同时满足 「样本属于 ckc_kck」且「特征取值为 ajla_{jl}ajl」的次数
分母：类别 ckc_kck 出现的总次数

4.2.2 学习与分类算法

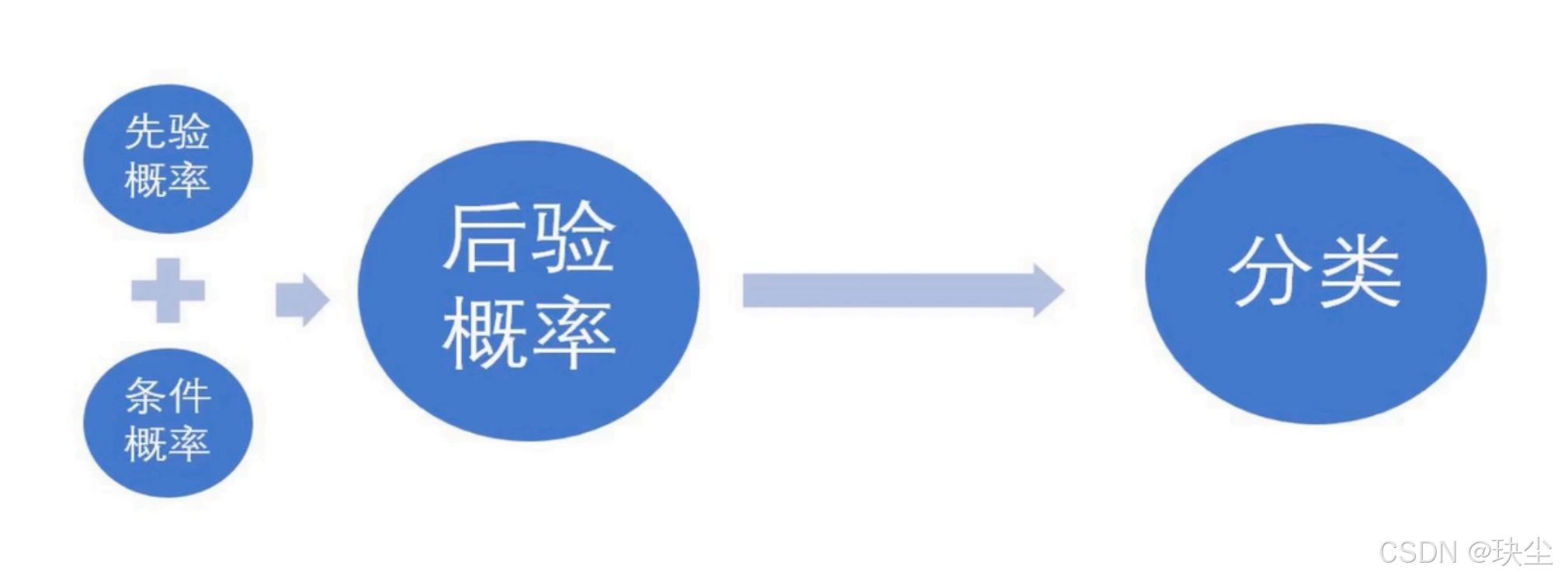
算法目标

如果有「一个实例点 x」，想通过朴素贝叶斯的分类法找到它「对应的类别 y」。

算法过程

先求出先验概率和条件概率（学习系统得到一个模型的过程）
P(Y=ck)=1N∑i=1NI(yi=ck)P(Y=c_k)=\frac{1}{N}\sum_{i=1}^N I(y_i=c_k)P(Y=ck)=N1i=1∑NI(yi=ck)
求出一系列的条件概率（学习系统得到一个模型的过程）
P(X(j)=ajl∣Y=ck)∑i=1NI(xi(j)=ajl, yi=ck)∑i=1NI(yi=ck)P(X^{(j)} = a_{jl}\mid Y=c_k) \frac{\sum_{i=1}^N I(x_i^{(j)}=a_{jl},\ y_i=c_k)} {\sum_{i=1}^N I(y_i=c_k)}P(X(j)=ajl∣Y=ck)∑i=1NI(yi=ck)∑i=1NI(xi(j)=ajl, yi=ck)
把各类的先验概率和条件概率连乘，得出计算结果最大值，就是对应的类
y=arg⁡max⁡ckP(Y=ck)∏jP(X(j)=x(j)∣Y=ck)y = \arg\max_{c_k} P(Y = c_k) \prod_j P(X^{(j)} = x^{(j)} | Y = c_k) y=argckmaxP(Y=ck)j∏P(X(j)=x(j)∣Y=ck)

例题解析

4.2.3 贝叶斯估计

在用极大似然估计概率时，我们完全依赖训练数据本身。如果数据分布不均衡，就会得到非常离谱的估计。比如我们想估计"女性在总体人口中的比例"，但训练数据来自"女儿国"，那极大似然就会给出 100% 都是女性 。显然，这不能代表真实情况。因此，我们需要一种方式来避免极端数据导致的极端结论，这就是贝叶斯估计存在的意义。

贝叶斯估计会在极大似然的公式里额外加上一些"先验信息"。

做法是：在计算先验概率和条件概率时，分子和分母都加上一个常数 λ\lambdaλ。当 λ=0\lambda = 0λ=0 时，它就退化成普通的极大似然估计。当 λ>0\lambda > 0λ>0 时，哪怕某些情况在训练集中从来没出现过，也不会被估计成 零概率。

「先验概率的贝叶斯估计」:

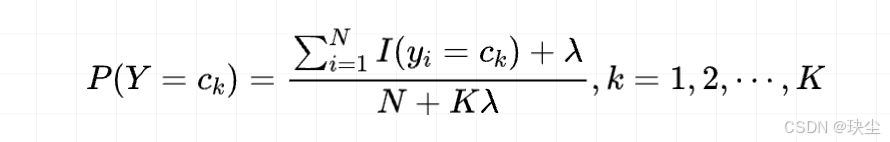
「条件概率的贝叶斯估计」:

实际中常用的是 λ=1\lambda = 1λ=1，也就是所谓的 拉普拉斯平滑。

⭐️为什么加了 𝜆 之后叫做"平滑"？

加入平滑系数 λ\lambdaλ 后，先验概率变为：

Pλ(Y=ck)=∑i=1NI(yi=ck)+λN+KλP_{\lambda}(Y = c_k) = \frac{\sum_{i=1}^{N} I(y_i = c_k) + \lambda}{N + K\lambda}Pλ(Y=ck)=N+Kλ∑i=1NI(yi=ck)+λ

为了推导更直观，我们把记号简化：

Pλ(Y=ck)=θk,∑i=1NI(yi=ck)=NkP_{\lambda}(Y = c_k)=\theta_k,\qquad \sum_{i=1}^{N} I(y_i = c_k) = N_kPλ(Y=ck)=θk,∑i=1NI(yi=ck)=Nk

代入后得：

θk(N+Kλ)=Nk+λ\theta_k(N + K\lambda) = N_k + \lambdaθk(N+Kλ)=Nk+λ

将等式重新整理：

(θkN−Nk)+λ(Kθk−1)=0(\theta_k N - N_k) + \lambda(K\theta_k - 1) = 0(θkN−Nk)+λ(Kθk−1)=0

前面这个式子为0，就是极大似然法，后面这个式子为0时，就是先验概率。这两个式子组成了凸组合。

例题讲解

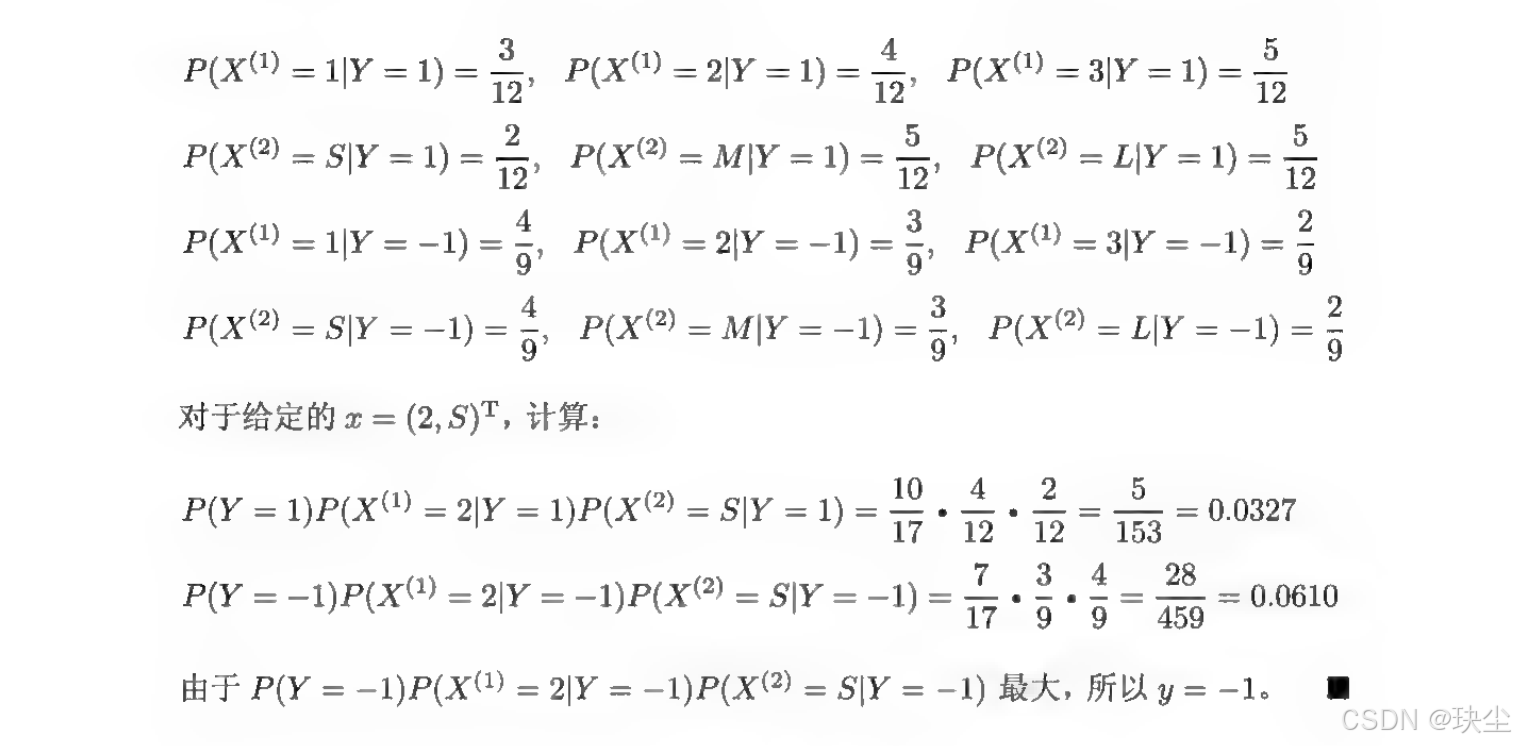
本章概要

1. 朴素贝叶斯法是典型的生成学习方法。 生成方法由训练数据学习联合概率分布 P(X,Y)P(X, Y)P(X,Y)，然后求得后验概率分布 P(Y∣X)P(Y|X)P(Y∣X)。具体来说，利用训练数据学习 P(X∣Y)P(X|Y)P(X∣Y) 和 P(Y)P(Y)P(Y) 的估计，得到联合概率分布：

P(X,Y)=P(Y)P(X∣Y)P(X, Y) = P(Y)P(X|Y)P(X,Y)=P(Y)P(X∣Y)

概率估计方法可以是极大似然估计或贝叶斯估计。

2. 朴素贝叶斯法的基本假设是条件独立性，

P(X=x∣Y=ck)=P(X(1)=x(1),⋯ ,X(n)=x(n)∣Y=ck)P(X = x|Y = c_k) = P(X^{(1)} = x^{(1)}, \cdots, X^{(n)} = x^{(n)}|Y = c_k)P(X=x∣Y=ck)=P(X(1)=x(1),⋯,X(n)=x(n)∣Y=ck)

=∏j=1nP(X(j)=x(j)∣Y=ck)= \prod_{j=1}^{n} P(X^{(j)} = x^{(j)}|Y = c_k)=j=1∏nP(X(j)=x(j)∣Y=ck)

这是一个较强的假设。由于这一假设，模型包含的条件概率的数量大为减少，朴素贝叶斯法的学习与预测大为简化。因而朴素贝叶斯法高效，且易于实现。其缺点是分类的性能不一定很高。

3. 朴素贝叶斯法利用贝叶斯定理与学到的联合概率模型进行分类预测。

P(Y∣X)=P(X,Y)P(X)=P(Y)P(X∣Y)∑YP(Y)P(X∣Y)P(Y|X) = \frac{P(X, Y)}{P(X)} = \frac{P(Y)P(X|Y)}{\sum_Y P(Y)P(X|Y)}P(Y∣X)=P(X)P(X,Y)=∑YP(Y)P(X∣Y)P(Y)P(X∣Y)

将输入 xxx 分到后验概率最大的类 yyy。

y=arg⁡max⁡ckP(Y=ck)∏j=1nP(Xj=x(j)∣Y=ck)y = \arg\max_{c_k} P(Y = c_k)\prod_{j=1}^{n} P(X_j = x^{(j)} \mid Y = c_k)y=argckmaxP(Y=ck)j=1∏nP(Xj=x(j)∣Y=ck)

后验概率最大等价于 0-1 损失函数时的期望风险最小化。