目录
前言
上文中介绍了最小方差自校正控制,《基于Matlab的最小方差自校正控制》提到了主要的两个缺点,要求对象是最小相位系统以及无输入约束,为了解决这些缺陷,提出里广义最小方差自校正控制。
一、广义最小方差自校正控制
广义最小方差自校正控制(Generalized Minimum Variance Self-Tuning Control, GMVSTC)是在最小方差自校正控制(Minimum Variance Self-Tuning Control, MVSTC) 基础上的改进与扩展,核心优势在于解决了 MVSTC 在实际工业场景中存在的局限性,更贴合复杂系统的控制需求。
GMVSTC 通过引入加权目标函数 和广义误差项, 实现 "精度 - 能耗 - 可靠性" 的多目标优化。加权目标函数还能抑制了高频控制分量,减少了噪声放大效应。目标函数的广义化也使控制律更平滑,降低了对模型参数误差的敏感
GMVSTC 的优点使其在工业控制中更具实用性,尤其适合以下场景:
- 有执行器约束的系统:如电机(电流 / 转速限制)、阀门(开度范围限制)、机械臂(力矩限制);
- 非最小相位系统:如某些化工过程、电磁耦合系统、含延迟的传动系统;
- 对能耗和设备损耗敏感的系统:如新能源设备、长期运行的工业生产线;
- 需要多目标优化的复杂系统:如机器人控制、精密制造设备、自动驾驶中的执行器控制。
但GMVSTC也有一个明显缺点,那就是对噪声很敏感,相比MVSTC会放大噪声。所以实际中一般搭配噪声滤波使用。
而 MVSTC 仅适用于简单的最小相位系统(如实验室中的低阶线性系统),且对控制输入无严格要求的场景(如仿真验证、理论研究)。
二、控制理论
有大量公式同前文,这里就简单解释。对于一个随机模型如下:
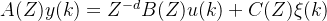
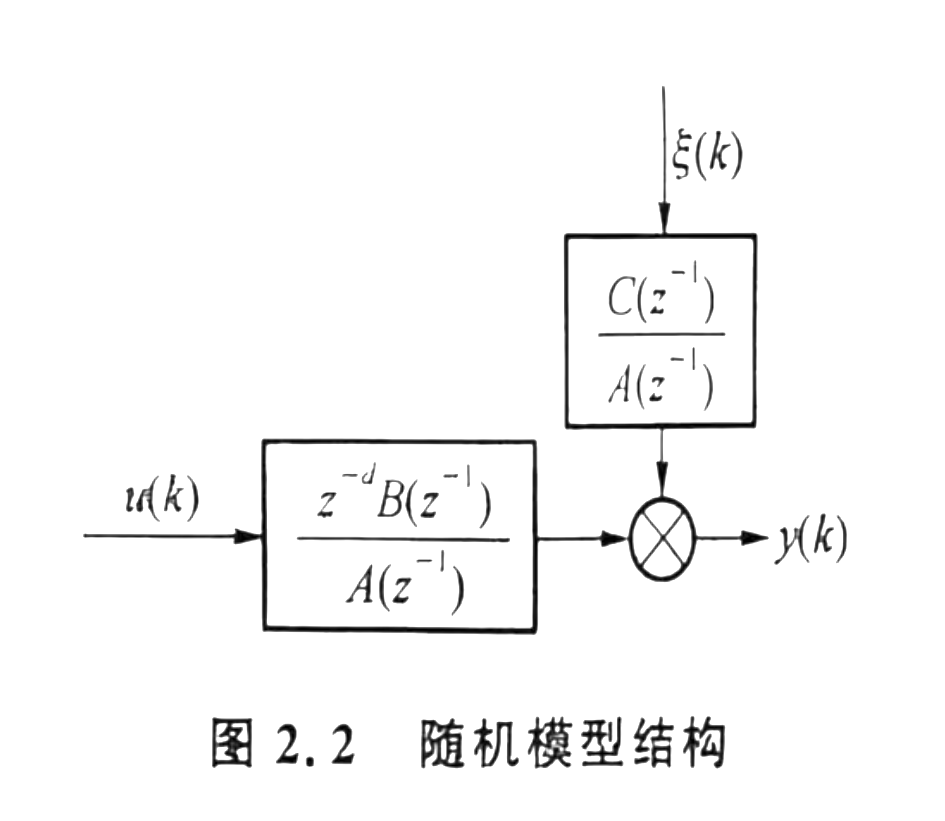
在最小方差自校正控制中选取的性能指标函数为:
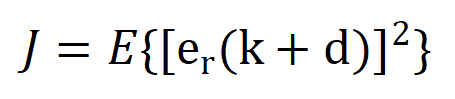
广义最小方差自校正控制有所不同,性能指标函数更改为:
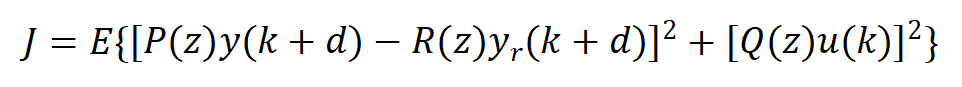
式中y(k+d),yr(k+d)分别为(k+d)时刻的系统实际输出及期望输出,u(k)为k时刻的输入,P(z)、R(z)、Q(z)为加权多项式,作用分别是改善系统闭环性能、柔化期望输出和约束输入信号,定义为:
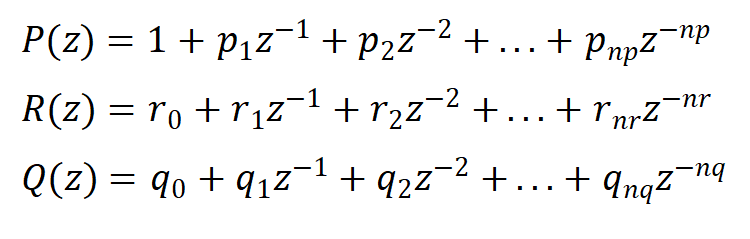
与最小方差自校正控制一样,有了性能指标函数,接下来解出使性能指标达到最优极小的表达式为最小控制律:
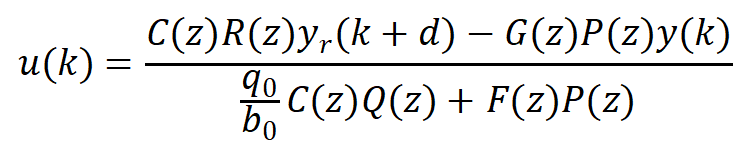
式中出现的G(z)、F(z)为丢番 (Diophantine) 方程的解,结合随机模型,得到广义最小方差自校正控制的结构框图为:
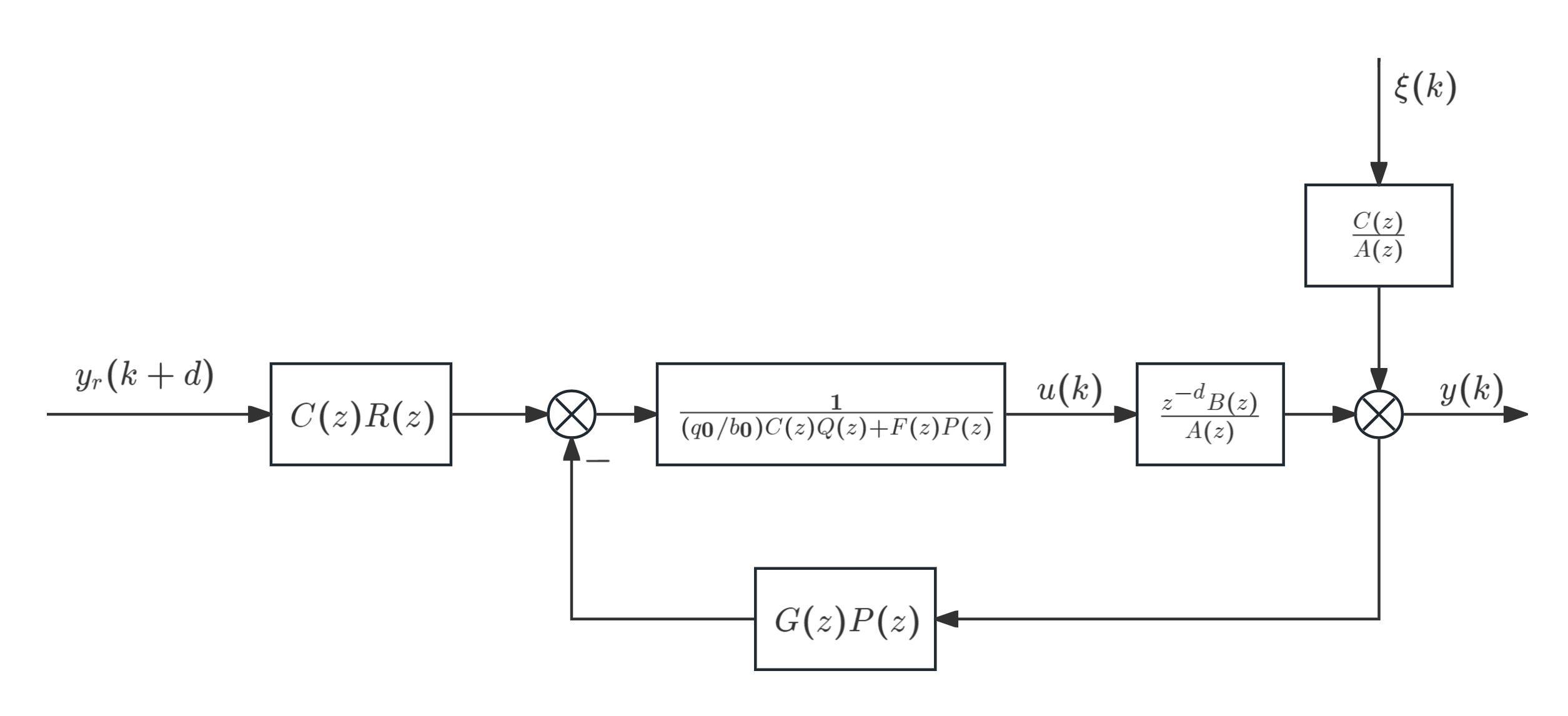
可以解的该系统的闭环特征方程为:
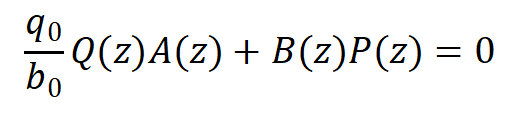
可以看出,即使B(z)为不稳定多项式,仍可通过选择合适的Q(z)和P(z)使系统稳定以及得到良好的闭环动态性能。如果Q(z) = 0,会发现性能指标函数不包含对u(k)的约束作用,而且特征方程变为B(z)P(z) = 0,B(z)的零点就是闭环极点,如果B(z)为非最小相位多项式此时系统不稳定,于是退化成最小方差自校正控制。
所以在进行系统设置中,一般可选P(z) = 1、R(z) = 1、Q(z) = q0。此时q0的大小要在稳定性和快速性之间权衡,若q0过小,接近于最小方差自校正控制,失去了作用。若q0过大,虽然稳定性能满足,但由于对u(k)的约束太强而使系统等效于开环状态,达不到最小方差控制的目的。当单独的q0难以达到理想状态,可以提高Q(z)的阶次。
另外,求得y(k)表达式(带入P(z) = 1、R(z) = 1、Q(z) = q0)为:
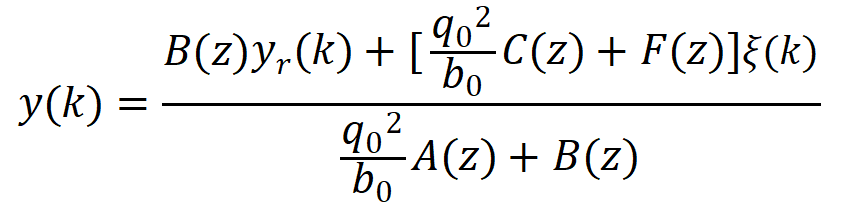
可知,q0会引入稳态误差,当q0 = 0时,y(k) = yr(k)、稳态误差为零,q0越大、稳态误差越大。但也不是绝对,当A(1) = 0时,q0就不会引入稳态误差。
另外,当q0越大,噪声所占比重就越大,当q0 = 0时,噪声比重达到最小。
三、举例说明
给定一个具体的系统模型如下:
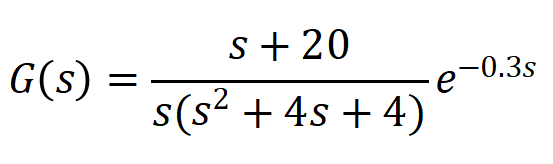
系统离散化。选取采用周期为0.1s,将系统进行零阶保持器的 Z 变换得到:
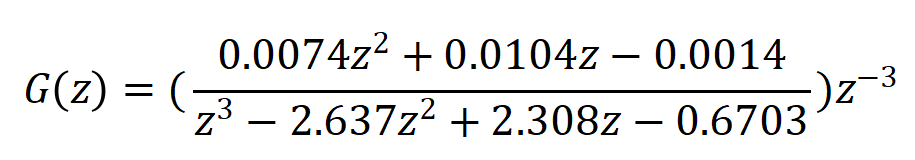
为了测试效果,给系统一个幅值为0,方差为0.1的噪声扰动信号,求得差分方程为:
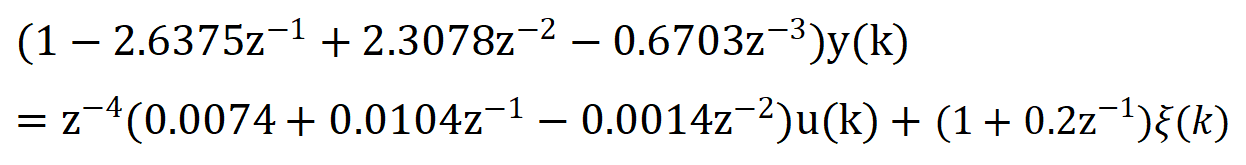
求得:
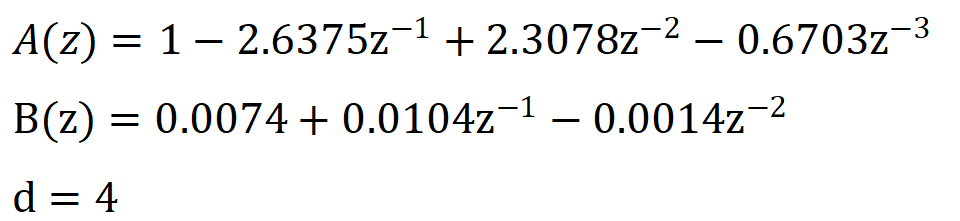
解的B(z)的极点为0,零点为0.1237和-1.5291,其中一个解位于单位圆外,为非最小相位系统,
接下来步骤同上文一样,直接看代码。
四、Matlab代码
Matlab
s = tf('s');%定义符号变量 s
%定义连续系统传递函数
G_continue = (s + 20) / (s*(s^2 + 4*s + 4)) * exp(-0.3*s);
T = 0.1; %采样周期 (单位:秒)
method = 'zoh'; %离散化方法:零阶保持器
G_discrete = c2d(G_continue, T, method); %连续系统离散化
[GB,GA] = tfdata(G_discrete); %提取分子、分母系数
GA = GA{1}; GB = GB{1}(2:numel(GB{1}));
GC = [1 0.2]; d = 4;%其他参数
GP = 1; GR = 1; GQ = 0.3;%P(z) = 1、R(z) = 1、Q(z) = q0;
%计算各多项式的阶次
nA = length(GA)-1;
nB = length(GB)-1;
nC = length(GC)-1;
nE = d-1;
nG = nA-1;
nF = nB+d-1;
L = 4000;%计算步长
yr = 100*[ones(1,L/4) -ones(1,L/4) ones(1,L/4) -ones(1,L/4)];%期望输出
u_noise = sqrt(0.01) * randn(1,L);%噪声信号
%u_noise = zeros(1,L);
[Ge,Gf,Gg] = sindiophantine(GA,GB,GC,d); %丢番方程计算
% T(z)u(k) = C(z)yr(k+d) - Gy(k)
GT = zeros(1,nF+1);
GT(1:nC+1) = GQ^2 * GC/GB(1) + Gf(1:nC+1)*GR;
GT(nC+2:nF+1) = Gf(nC+2:nF+1);
%空间分配
time = zeros(1,L);
y = zeros(1,L);
u = zeros(1,L);
%让t=10设为0时刻,则之前的时刻方便表达
t = 10;
for k=t:L-t
time(k) = k-t+1;
y(k) = -GA(2:nA+1)*[y(k-1);y(k-2);y(k-3)]+GB*[u(k-4);u(k-5);u(k-6)]+GC*[u_noise(k);u_noise(k-1)];
u(k) = (-GT(2:nF+1)*[u(k-1);u(k-2);u(k-3);u(k-4);u(k-5)]+GC*GR*[yr(k+4);yr(k+3)]-Gg*GP*[y(k);y(k-1);y(k-2)])/GT(1);
end
figure(1);
subplot(2,1,1);
plot(time(t:L-t),yr(t:L-t),'r',time(t:L-t),y(t:L-t),'b--');
xlabel('k');ylabel('yr(k)、y(k)');
legend('期望输出yr(k)','实际输出y(k)');
grid on;
subplot(2,1,2);
plot(time(t:L-t),u(t:L-t));
xlabel('k');ylabel('u(k)');
legend('输入u(k)');
grid on;五、结果分析
阶跃信号幅值为10,q0为0.3,无噪声:
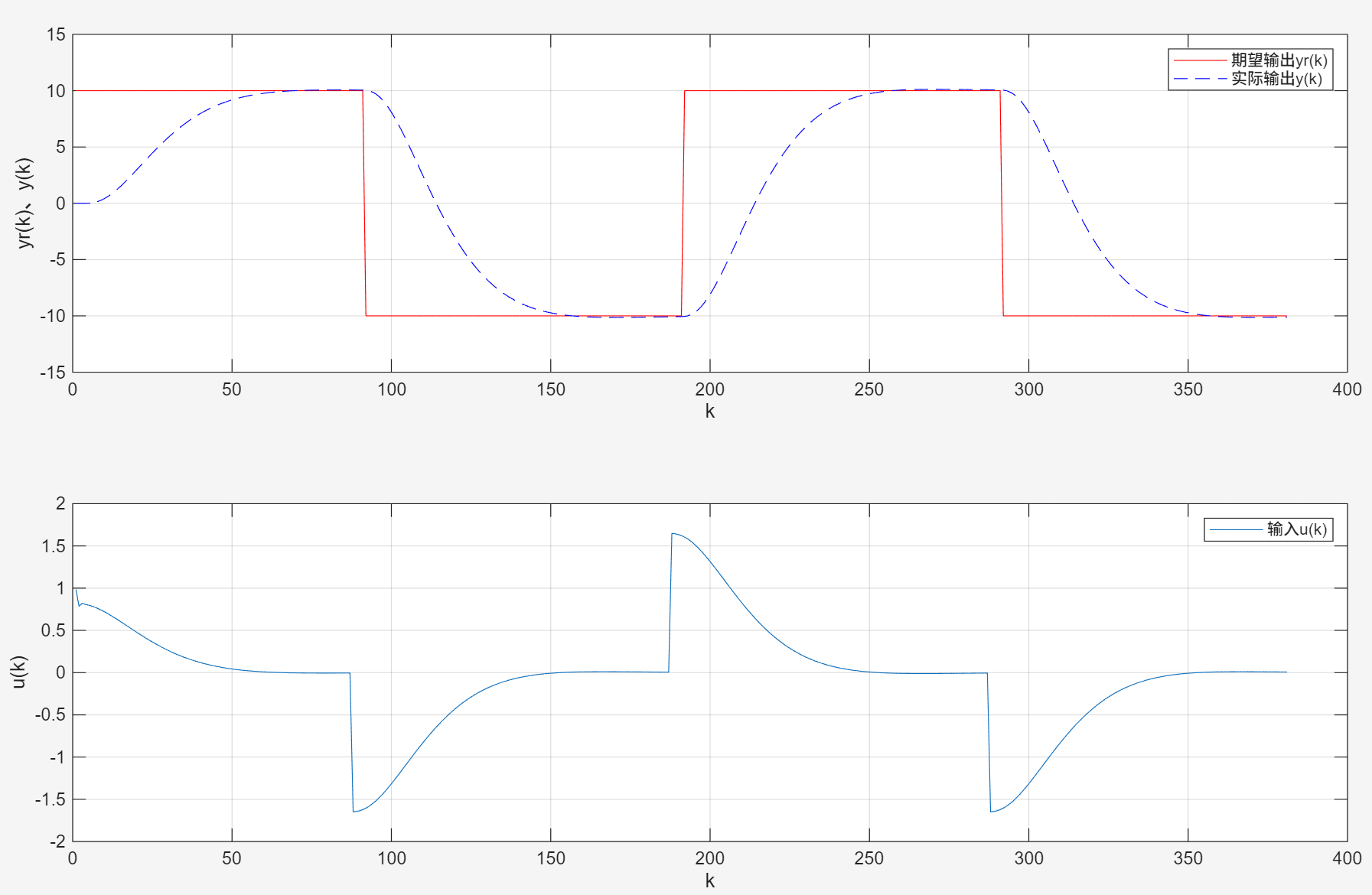
阶跃信号幅值为10,q0为1,无噪声:
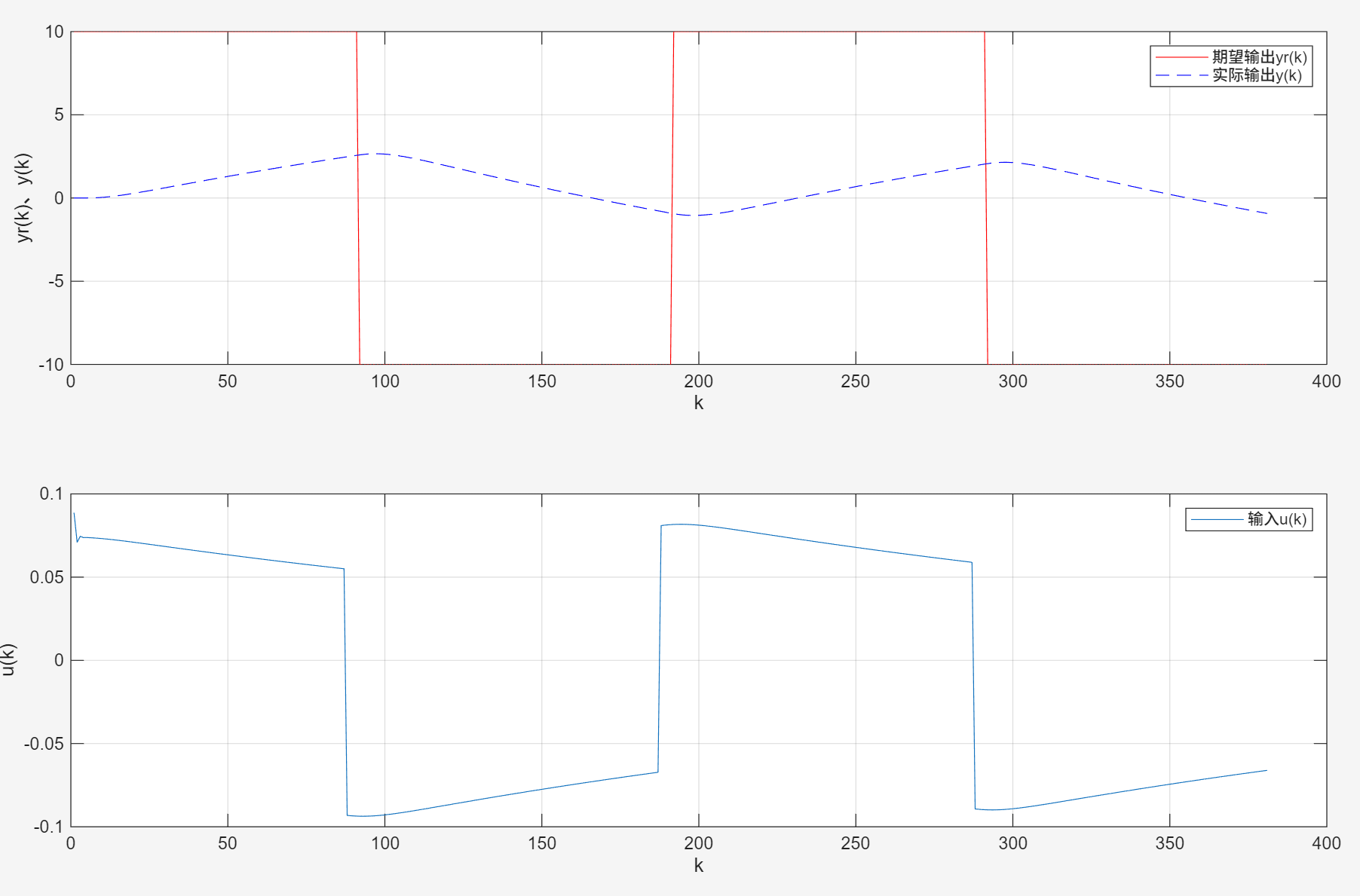
可以看出,增大q0会加大u(k)的约束,但同时上升缓慢,动态性能减弱。
阶跃信号幅值为10,q0为0.3,引入方差为0.1的噪声:
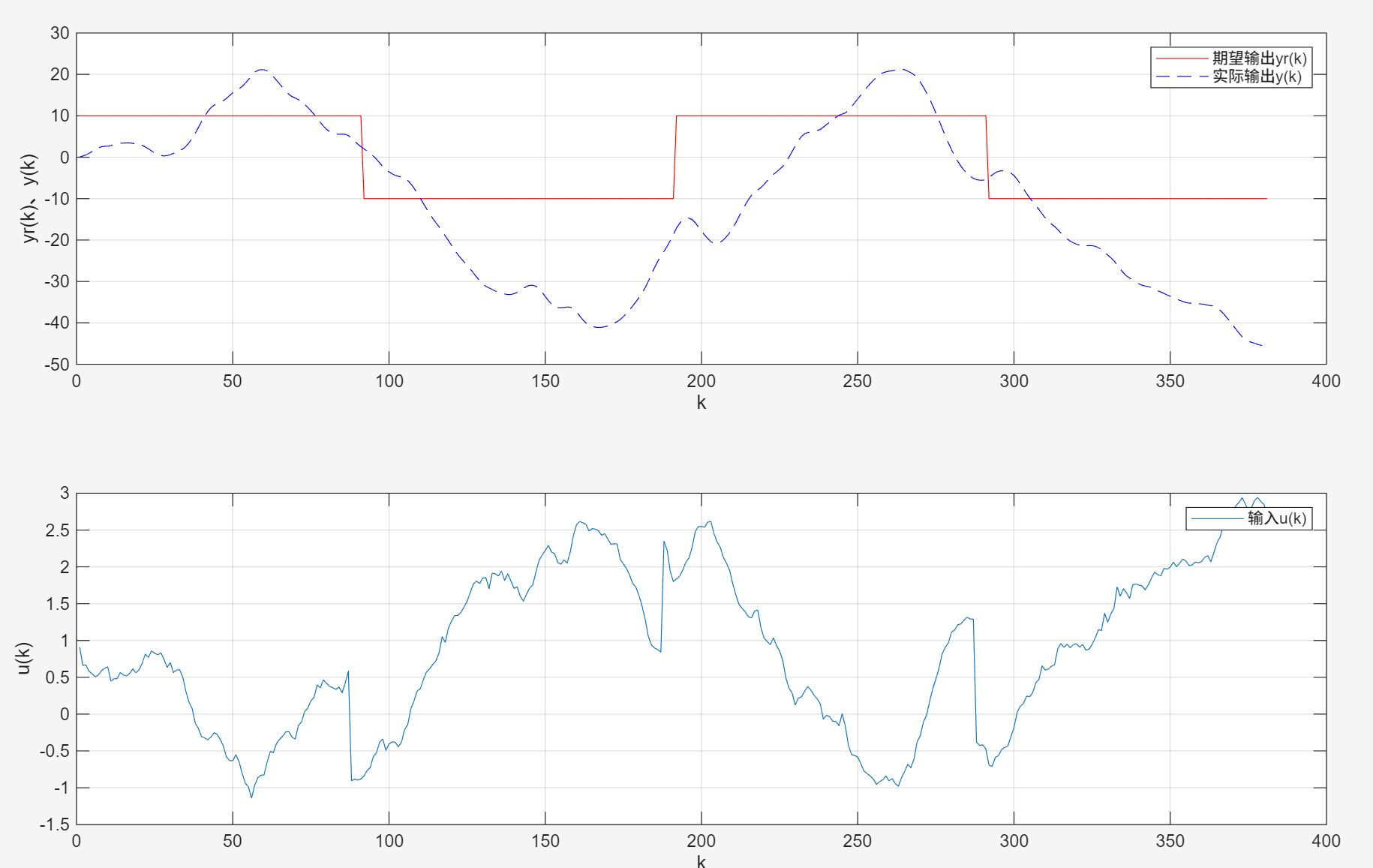
阶跃信号幅值为100,q0为0.3,引入方差为0.1的噪声:
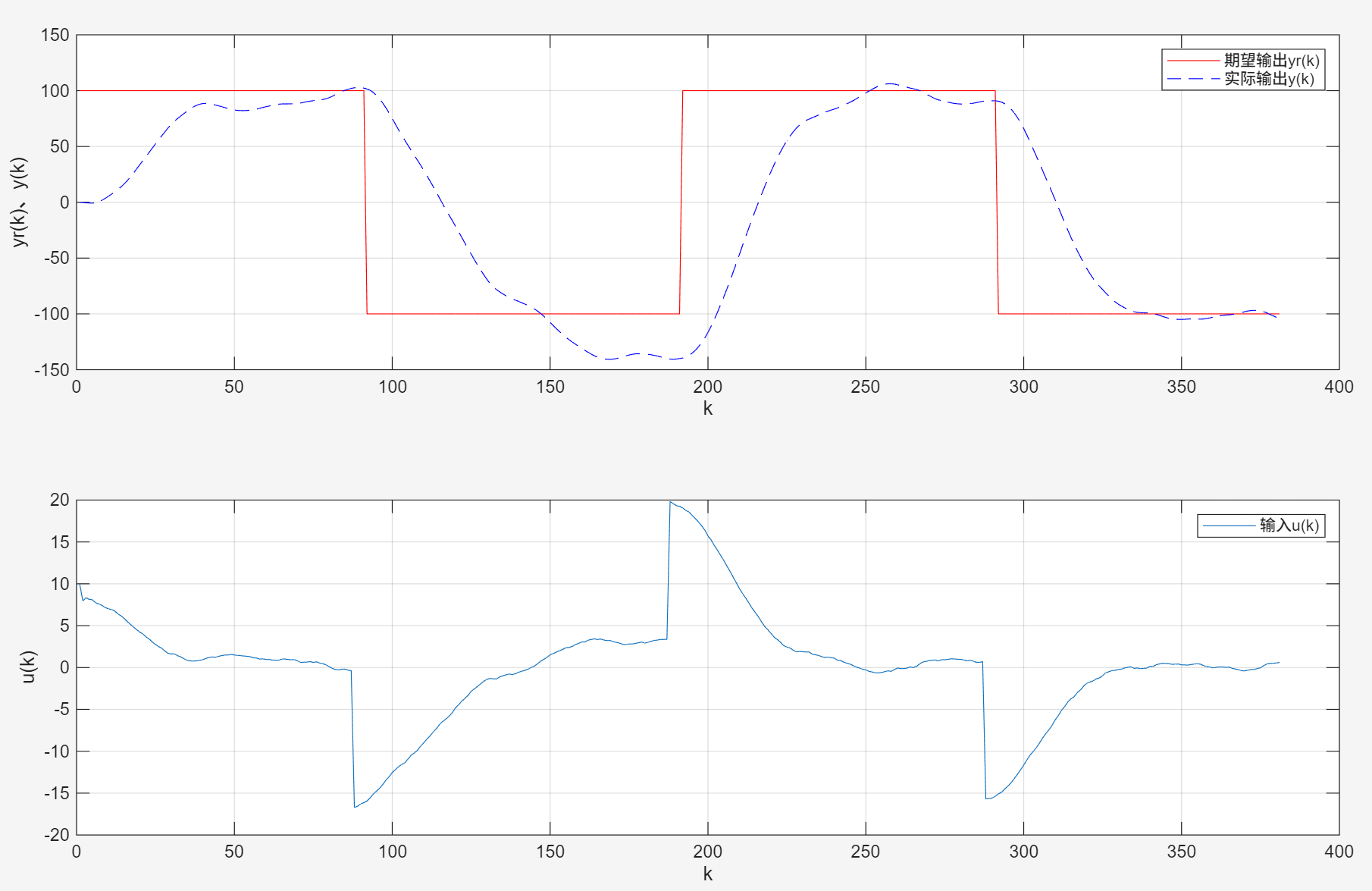
可以看出幅值越大,噪声的影响约小。
阶跃信号幅值为100,q0为0.3,引入方差为0.1的噪声,步长增加到4000:
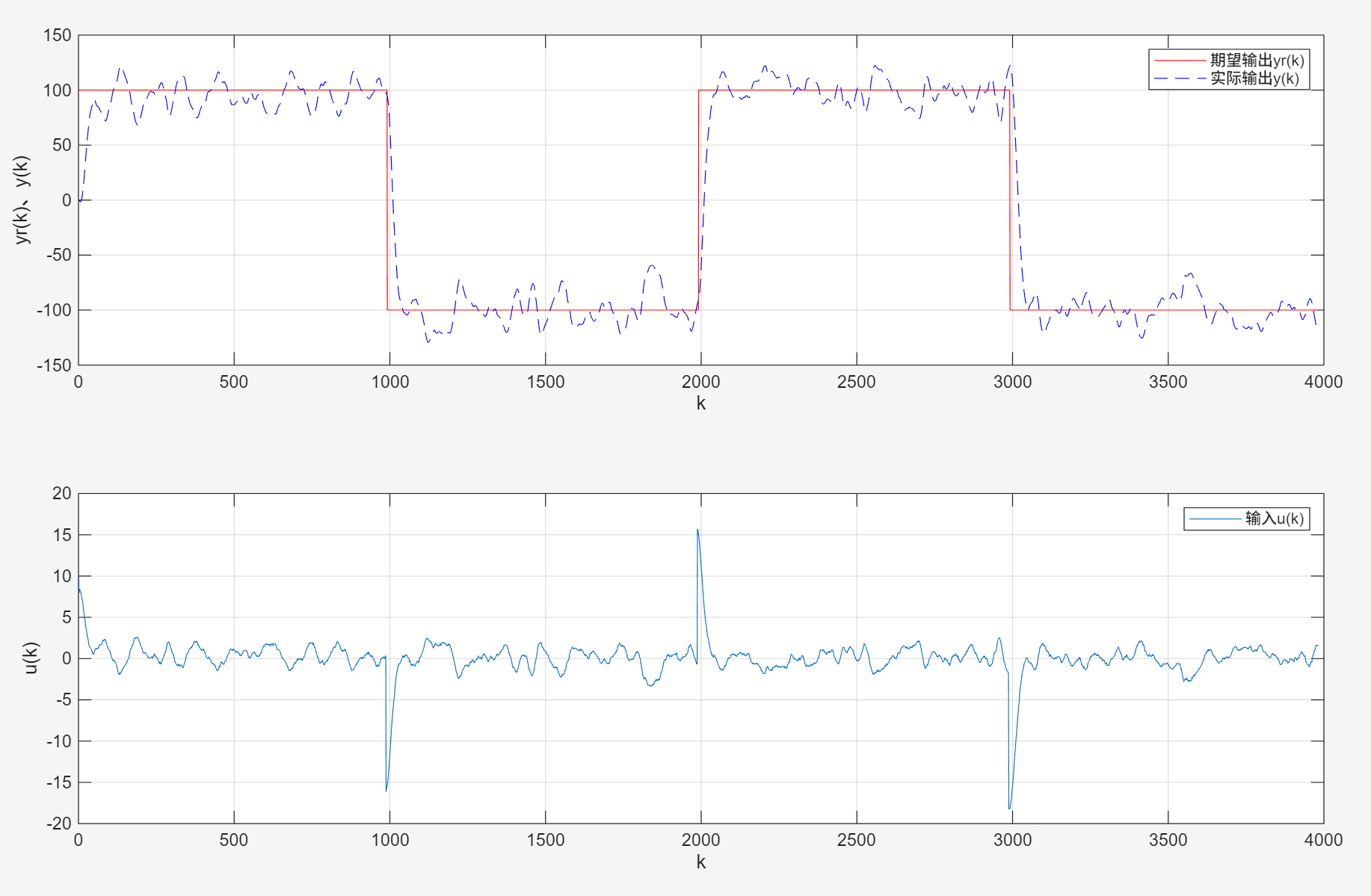
总结
广义最小方差自校正控制相比最小方差自校正控制会扩大噪声,实际中光靠广义最小方差自校正控制本身很难控制下来。
增加q0:稳态误差增大(非常不明显),动态性能减弱(非常明显),对u(k)的约束增强