最近在学习 AI (尤其是大模型和 RAG) 的过程中, 我发现 向量 (Vector) 是理解这一切的基础
为了帮助大家跨越数学门槛, 我整理了这份指南, 尝试把抽象的数学概念与 AI 的实际应用结合起来, 带你从底层逻辑理解 AI 是如何"思考"的
我是印刻君,一位探索 AI 的程序员,关注我,了解更多有温度的轻知识,有深度的硬内容
第一部分: 向量的基础认知
1. 什么是向量?
在数学和物理学中, 我们通常将"量"分为两类:
- 标量 (Scalar) : 只有大小 , 没有方向
- 例子: 今天的气温是 25 摄氏度;我的体重是 60 公斤
- 向量 (Vector) : 既有大小 又有方向
- 例子: 北风 4 级(风速是大小, 北方是方向);向东走 500 米(500 米是大小, 向东是方向)
🤔 为什么 AI 需要使用向量, 而且是高维向量?
现实世界极其复杂, 单一的数字(标量)往往无法完整描述一个事物
如果说二维向量让我们能够同时描述"大小"和"方向", 那么高维向量 则赋予了我们精确描述事物成百上千种特征的能力
在计算机科学中, 向量的每一个维度都可以被理解为一种特征 (Feature)
所谓高维向量, 本质上就是多种特征的组合:
举个例子, 要描述一个"苹果", 光说"甜度 5"是不够的如果我们构建一个特征向量 (颜色, 甜度, 脆度), 例如 (0.9, 5, 8), AI 就能精准知道: "这是一个颜色很红、中等甜度、非常脆的苹果"
当维度扩展到成百上千维时, AI 就能捕捉到人类语言中极其微妙的语义差别
2. 向量的表示: 从图像到坐标
在几何意义上, 二维向量通常表示为一个带箭头的线段:
- 箭头的指向: 代表方向
- 线段的长度: 代表大小(模)
如下图所示, 这是一个从 <math xmlns="http://www.w3.org/1998/Math/MathML"> A ( 0 , 0 ) A(0, 0) </math>A(0,0) 点指向 <math xmlns="http://www.w3.org/1998/Math/MathML"> B ( 3 , 4 ) B(3, 4) </math>B(3,4) 点的向量:
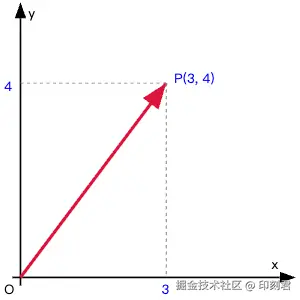
💻 为什么计算机里只存坐标 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( x , y ) (x, y) </math>(x,y)?
你可能会问: "向量不是要有起点和终点吗?为什么代码里通常只写 [0.12, 0.88] 这种数组?"
这是因为在计算机处理中, 为了统一标准, 我们通常使用位置向量 (Position Vector) ------ 将所有向量的起点都固定在坐标原点 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( 0 , 0 ) (0, 0) </math>(0,0)
既然起点是固定的, 我们只需要记录终点的坐标, 就等同于确定了整个向量
转换公式 : 如果一个向量是从任意点 <math xmlns="http://www.w3.org/1998/Math/MathML"> A ( x 1 , y 1 ) A(x_1, y_1) </math>A(x1,y1) 指向 <math xmlns="http://www.w3.org/1998/Math/MathML"> B ( x 2 , y 2 ) B(x_2, y_2) </math>B(x2,y2), 我们可以通过"终点减起点"将其转换为标准位置向量:
<math xmlns="http://www.w3.org/1998/Math/MathML"> A B ⃗ = ( x 2 − x 1 , y 2 − y 1 ) \vec{AB} = (x_2 - x_1, y_2 - y_1) </math>AB =(x2−x1,y2−y1)
第二部分: 向量的加减与模
理解了向量的表示后, 我们来看看向量的基本运算, 以及它们在 AI 语义理解中的核心作用
1. 加法与减法: 语义的推演
向量的加减法遵循对应分量相加减的规则:
- <math xmlns="http://www.w3.org/1998/Math/MathML"> a ⃗ + b ⃗ = ( x 1 + x 2 , y 1 + y 2 ) \vec{a} + \vec{b} = (x_1+x_2, y_1+y_2) </math>a +b =(x1+x2,y1+y2)
- <math xmlns="http://www.w3.org/1998/Math/MathML"> a ⃗ − b ⃗ = ( x 1 − x 2 , y 1 − y 2 ) \vec{a} - \vec{b} = (x_1-x_2, y_1-y_2) </math>a −b =(x1−x2,y1−y2)
在几何上, 这遵循"平行四边形法则"或"三角形法则"
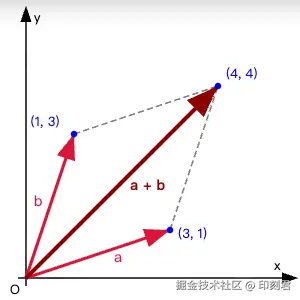
💡 AI 案例: 词向量的加减运算
向量加减法, 本质上就是特征的叠加或抵消
- 加法: 把两个概念融合
- 减法: 把某个特征去掉
经典的例子是: 王子 - 男人 + 女人 = ?
为了便于理解, 假设我们的词向量只有两个维度(实际上通常几百维或更多):
- x 轴代表性别(数值越大越女性化)
- y 轴代表地位(数值越大越尊贵)
我们定义以下坐标:
- 王子 :
(1, 9)[男性, 尊贵] - 男人 :
(1, 1)[男性, 普通] - 女人 :
(9, 1)[女性, 普通]
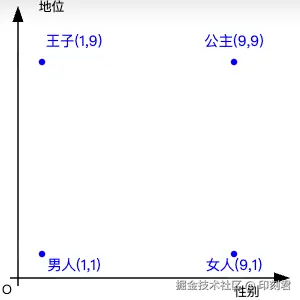
现在进行运算:
王子 - 男人:(1, 9) - (1, 1) = (0, 8)这一步去除了"男性"属性, 保留了"尊贵"属性(即纯粹的"皇室地位"概念)+ 女人:(0, 8) + (9, 1) = (9, 9)将"女性"属性叠加到"皇室地位"上
结果 (9, 9) 对应的是 [女性, 尊贵] , 在向量空间中, 这个坐标最接近的词就是 公主
这就是大语言模型理解"语义"的基础逻辑: 通过向量空间中的位置关系, 来表征词与词之间的逻辑关联
2. 向量的模(Magnitude / Length)
向量的模 (也叫长度)是一个标量, 表示向量的大小通常记作 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ v ⃗ ∣ |\vec{v}| </math>∣v ∣ 或 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ ∣ v ⃗ ∣ ∣ ||\vec{v}|| </math>∣∣v ∣∣
根据初中学的勾股定理, 二维向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> ( x , y ) (x, y) </math>(x,y) 的模为:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ v ⃗ ∣ = x 2 + y 2 |\vec{v}| = \sqrt{x^2 + y^2} </math>∣v ∣=x2+y2
举个例子:
如果向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> v ⃗ = ( 3 , 4 ) \vec{v} = (3, 4) </math>v =(3,4), 那么它的模就是:
<math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ v ⃗ ∣ = 3 2 + 4 2 = 9 + 16 = 25 = 5 |\vec{v}| = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 </math>∣v ∣=32+42 =9+16 =25 =5
💡 AI 案例: 模的作用
归一化 (Normalization) : 在 AI 应用中, 有时我们只关心向量的方向(代表内容主题), 而不关心其长度(代表文本长短或词频)此时, 我们会将向量除以它的模, 使其变为单位向量(长度为 1)这样做可以消除文本长度对相似度计算的影响
第三部分: 衡量向量间的关系(相似度)
在 AI 中, 判断两个对象(文本、图片)是否相似, 本质上就是计算它们对应向量之间的距离或夹角
1. 点乘 (Dot Product)
点乘是计算相似度的数学基础, 其结果是一个标量
- 代数定义 : 对应分量相乘再求和 <math xmlns="http://www.w3.org/1998/Math/MathML"> a ⃗ ⋅ b ⃗ = x 1 x 2 + y 1 y 2 \vec{a} \cdot \vec{b} = x_1x_2 + y_1y_2 </math>a ⋅b =x1x2+y1y2
- 几何定义 : <math xmlns="http://www.w3.org/1998/Math/MathML"> a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ × ∣ b ⃗ ∣ × cos ( θ ) \vec{a} \cdot \vec{b} = |\vec{a}| \times |\vec{b}| \times \cos(\theta) </math>a ⋅b =∣a ∣×∣b ∣×cos(θ)
- <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ a ⃗ ∣ |\vec{a}| </math>∣a ∣ 和 <math xmlns="http://www.w3.org/1998/Math/MathML"> ∣ b ⃗ ∣ |\vec{b}| </math>∣b ∣ 分别是向量 a 和 b 的模(长度)
- <math xmlns="http://www.w3.org/1998/Math/MathML"> θ \theta </math>θ 是两个向量之间的夹角
2. 余弦相似度 (Cosine Similarity)
利用点乘公式, 我们可以推导出两个向量夹角的余弦值, 这就是最常用的余弦相似度:
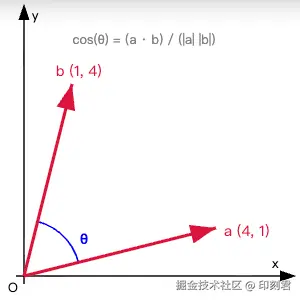
<math xmlns="http://www.w3.org/1998/Math/MathML"> Similarity = cos ( θ ) = a ⃗ ⋅ b ⃗ ∣ a ⃗ ∣ × ∣ b ⃗ ∣ \text{Similarity} = \cos(\theta) = \frac{\vec{a} \cdot \vec{b}}{|\vec{a}| \times |\vec{b}|} </math>Similarity=cos(θ)=∣a ∣×∣b ∣a ⋅b
数值含义:
- 1 ( <math xmlns="http://www.w3.org/1998/Math/MathML"> θ = 0 ∘ \theta = 0^\circ </math>θ=0∘): 方向完全相同(语义极度相似)
- 0 ( <math xmlns="http://www.w3.org/1998/Math/MathML"> θ = 9 0 ∘ \theta = 90^\circ </math>θ=90∘): 相互垂直(毫无关系, 正交)
- -1 ( <math xmlns="http://www.w3.org/1998/Math/MathML"> θ = 18 0 ∘ \theta = 180^\circ </math>θ=180∘): 方向完全相反(语义对立)
为什么 AI 偏爱余弦相似度?
因为它关注的是方向而非距离
- 例子: 一句简短的"我爱编程"和一篇 5000 字赞美编程技术的文章
- 它们的向量方向非常接近(都在讨论编程主题), 因此余弦相似度很高
- 但由于文本长度差异巨大, 长文章的向量模长很大, 两者在空间中的欧氏距离会很远在这种场景下, 余弦相似度更能反映语义的一致性
3. 欧氏距离 (Euclidean Distance)
即两点间的直线距离, 也就是连接两个向量终点的线段长度:
<math xmlns="http://www.w3.org/1998/Math/MathML"> Distance = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 \text{Distance} = \sqrt{(x_1-x_2)^2 + (y_1-y_2)^2} </math>Distance=(x1−x2)2+(y1−y2)2
💡 适用场景 数值的大小(量级)非常关键时, 使用欧氏距离
- 例子: 电商用户聚类
- 用户 A: 购买 1 个苹果
- 用户 C: 购买 2 个苹果
- 用户 B: 购买 1000 个苹果(批发商)
- 虽然三者购买方向一致(都是苹果), 但 A 和 C 的**消费能力(距离)**更近系统会将 A 和 C 归为普通消费者, 而将 B 归为商业客户
第四部分: 从二维到高维 AI 世界
在 AI 领域, 向量通常拥有几百甚至几千个维度(例如 OpenAI 的 text-embedding-3-small 模型是 1536 维)虽然我们无法在脑海中构想出高维图像, 但数学规则是完全一致的:
假设向量 <math xmlns="http://www.w3.org/1998/Math/MathML"> A = ( a 1 , . . . , a n ) A = (a_1, ..., a_n) </math>A=(a1,...,an), <math xmlns="http://www.w3.org/1998/Math/MathML"> B = ( b 1 , . . . , b n ) B = (b_1, ..., b_n) </math>B=(b1,...,bn)
- 加法: 对应位相加
- 模 : <math xmlns="http://www.w3.org/1998/Math/MathML"> a 1 2 + . . . + a n 2 \sqrt{a_1^2 + ... + a_n^2} </math>a12+...+an2
- 点乘 : <math xmlns="http://www.w3.org/1998/Math/MathML"> a 1 b 1 + . . . + a n b n a_1b_1 + ... + a_n b_n </math>a1b1+...+anbn
总结来说, 我们可以用加法 对词语的各种特征进行组合, 用模 来衡量强度, 用点乘来抽象地计算相似度
总结
本文系统性地介绍了向量在 AI 中的核心作用:
- 核心概念
- 向量:兼具大小和方向的数学对象,是 AI 表示复杂特征的基础
- 高维向量:能够同时编码数百种语义特征,实现精细的语义理解
- 关键运算及其意义
- 加减法:实现语义的组合与推演(如"国王 - 男人 + 女人 = 王后")
- 模(长度):衡量特征强度,用于归一化处理
- 点乘与余弦相似度:计算语义相似性,是检索和匹配的核心
- 实际价值 向量为 AI 提供了一种可计算的语义表示方法 ,使得:
- 计算机能够"理解"词语间的逻辑关系
- 实现基于语义的智能搜索和推荐
- 构建更准确的自然语言处理系统
我是印刻君,一位探索 AI 的程序员,关注我,了解更多有温度的轻知识,有深度的硬内容。
本文略过了叉乘(Cross Product), 因为它主要用于 3D 图形学(计算法线等), 在 AI 语义分析中极少使用