二叉搜索树
一、什么是二叉搜索树
二叉搜索树也叫做二叉排序树,是在二叉树的基础上增加了更多的限制条件产生的一种树,限制具体如下:
二叉搜索树整体呈现根节点的左子树小于此根节点的值,右子树大于此根节点的值,每一棵左右子树也遵循此规则,同时中可以⽀持插⼊相等的值,也可以不⽀持插⼊相等的值,但是一般不⽀持插⼊相等的值。
二叉搜索树举例:
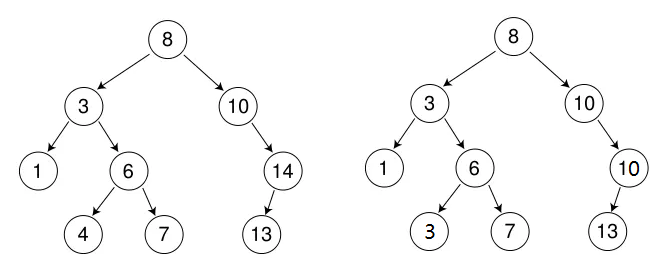
二、二叉搜索树的简单实现
2.1整体结构
C++定义二叉搜索树,首先定义节点结构,使用struct定义公共节点类,将这个类定义为模板类,方便定义不同类型的二叉搜索树:
cpp
// 定义根节点类
template<class K>
struct BSTNode
{
K _key;
BSTNode<K>* _left;
BSTNode<K>* _right;
// 构造节点
BSTNode(const K& key)
:_key(key)
,_left(nullptr)
,_right(nullptr)
{}
};随后使用节点来构造树tree。
cpp
// 定义二叉搜索树类
template<class K>
class BSTree
{
// 重命名BSTNode<K>类型
typedef BSTNode<K> node;
public:
// ..方法
private:
// 属性 --- 节点
node* _root = nullptr;
};2.2插入
二叉搜索树的插入严格遵循对于每一个根节点,其左子树都小于根节点,右子树都大于根节点:
注意:规定本树不可以插入相同的值。
cpp
// 插入
/*
* 调用方法传key
* (1)若二叉搜索树为空(nullptr),则直接通过key创建一个根节点
* (2)先找到合适的插入位置,创建cur和parent,锁定插入位置和插入位置的父节点
* (3)插入的key比插入位置的父节点的key小,则作为左孩子链接
* 插入的key比插入位置的父节点的key大,则作为右孩子链接
*/
bool Insert(const K& key)
{
// 一开始树为空,直接将key插入作为根节点
if (_root == nullptr)
{
_root = new node(key);
return true;
}
// 找到待插入key值的位置
node* parent = nullptr;
node* cur = _root;
while (cur)
{
// 比key小,向下找左子树
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
// 比key大,向下找右孩子
else if(key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
// 不允许插入相等key值
else
{
return false;
}
}
// while运行完毕,代表找到了合适的位置
// 此时cur指向nullptr
cur = new node(key);
// 插入key比找到的位置的前一个节点的key小,则链接为左孩子
if (key < parent->_key)
{
parent->_left = cur;
}
// 插入key比找到的位置的前一个节点的key大,则链接为右孩子
else if(key > parent->_key)
{
parent->_right = cur;
}
// 成功的插入返回true
return true;
}构造一棵二叉搜索树:
cpp
BSTree<int> tree;
int arr[] = { 2,4,7,9,1,5,6,8,3,10 };
for (auto e : arr)
{
tree.Insert(e);
}构造出来的树为:
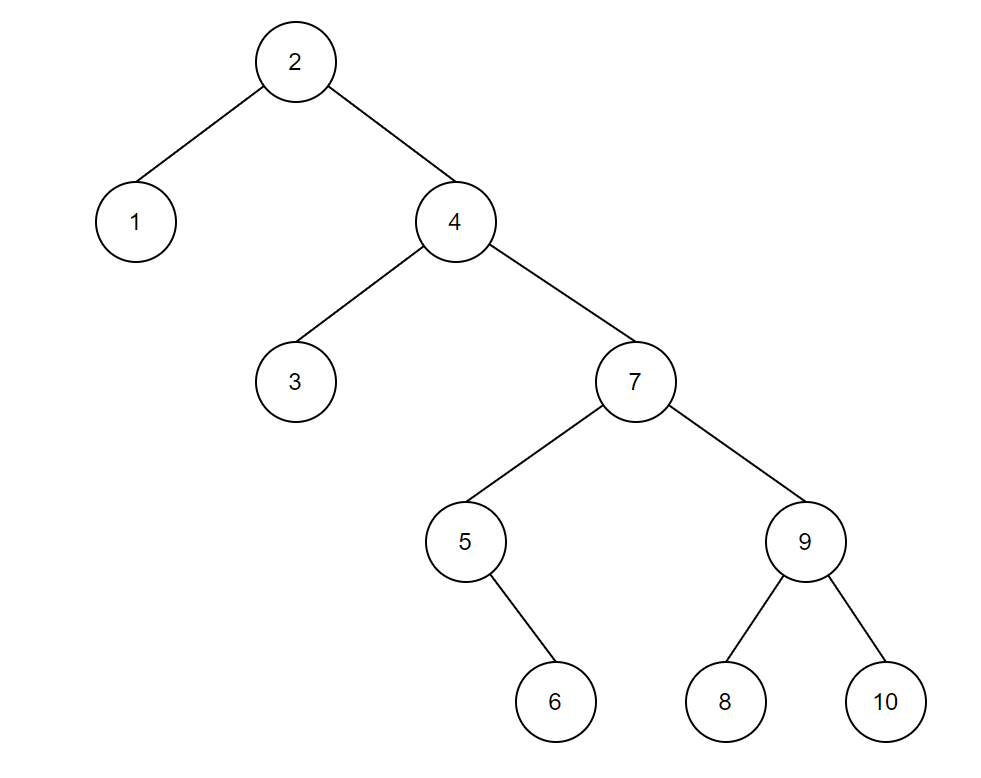
2.3查找
查找的逻辑非常简单,首先找到这个节点,返回true/false即可,找节点的算法和插入节点中找到合适位置的插入算法是一模一样的:
cpp
// 查找
bool Find(const K& key)
{
// 找到key值的位置
node* parent = nullptr;
node* cur = _root;
while (cur)
{
// 比key小,向下找左子树
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
// 比key大,向下找右孩子
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
// key值相等,代表找到了,和插入方法中的唯一区别
else
{
return true;
}
}
return false;
}2.4删除
对于节点的删除是二叉搜索树中最麻烦的一个算法,分为以下五种情况:
(1)当删除节点是叶子节点的时候,直接delete掉即可
(2)当删除节点是当前节点的父节点的左孩子时,且删除节点的左孩子为空(代表右孩子存在),则需要将父节点的左链接到删除节点的右
(3)当删除节点是当前节点的父节点的右孩子时,且删除节点的右孩子为空(代表左孩子存在),则需要将父节点的右链接到删除节点的左。
(4)当删除节点的左右孩子都存在,则使用向下替换节点进行间接删除:
在情况4中又有两种方法可以选择,向下找左子树最大节点,或者向下找右子树最小节点,原因还是二叉搜索树的特点,根节点的左子树永远比根节点小,根节点的右子树永远比根节点大,找到之后进行交换,以保证删除节点时整棵树的结构不会发生破坏。
(5)当删除节点是根节点时,直接让删除节点的左孩子或者右孩子作为根节点即可。
上述第一点可以和第二点/第三点合并,只不过父节点左/右指向成了nullptr。
cpp
// 删除 --- 核心思想是向下找替换key
// 替换的原则是:找需要删除节点的左子树最大key,或者找右子树最小key
bool Erase(const K& key)
{
if (_root == nullptr)
{
return false;
}
// 也是先找到key值的位置
node* parent = nullptr;
node* cur = _root;
while (cur)
{
// 比key小,向下找左子树
if (key < cur->_key)
{
parent = cur;
cur = cur->_left;
}
// 比key大,向下找右孩子
else if (key > cur->_key)
{
parent = cur;
cur = cur->_right;
}
// key值相等,代表找到了,准备删除
else
{
// 若待删除节点左孩子为空,则表明存在右孩子
if (cur->_left == nullptr)
{
// 如果删除节点不是根节点
if (cur != _root)
{
// 待删除节点是其父节点的左孩子,则让父节点的左链接删除节点的右
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
// 待删除节点是其父节点的右孩子,则让父节点的右链接删除节点的右
else if (cur == parent->_right)
{
parent->_right = cur->_right;
}
delete cur;
}
// 删除节点是根节点,则直接让删除节点的右成为根节点
else
{
_root = cur->_right;
}
}
// 若待删除节点右孩子为空,则表明存在左孩子
else if (cur->_right == nullptr)
{
if (cur != _root)
{
// 待删除节点是其父节点的左孩子,则让父节点的左链接删除节点的左
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
// 待删除节点是其父节点的右孩子,则让父节点的右链接删除节点的左
else if (cur == parent->_right)
{
parent->_right = cur->_left;
}
delete cur;
}
else
{
_root = cur->_left;
}
}
// 若待删除节点左右孩子均有,则向下找可替换key
else
{
// 这里找右子树最小key
node* minRightParent = cur;
node* minRight = cur->_right;
while (minRight->_left)
{
minRightParent = minRight;
minRight = minRight->_left;
}
// 找到了最小的key
std::swap(minRight->_key, cur->_key);
// 链接逻辑和上面if,elseif相同
if (minRight == minRightParent->_left)
{
minRightParent->_left = minRight->_left;
}
else if (minRight == minRightParent->_right)
{
minRightParent->_right = minRight->_left;
}
delete minRight;
}
return true;
}
}
return false;
}2.5遍历
二叉搜索树的遍历使用中序遍历方式,二叉搜索树的中序遍历结果是升序序列,所以说中序遍历同时也兼顾了排序的功能。
中序遍历的思想就是递归,依次按照每一棵树的左根右顺序进行遍历:
cpp
// 类中封装,类外直接.InOrder()访问
void InOrder()
{
inorder(_root);
std::cout << std::endl;
}
private:
// 遍历 --- 使用中序遍历,最终是升序序列
// 中序 --- 左根右
void inorder(const node* root)
{
if (root == nullptr)
{
return;
}
inorder(root->_left);
std::cout << root->_key << " ";
inorder(root->_right);
}方法演示:
cpp
int main()
{
BSTree<int> tree;
int arr[] = { 2,4,7,9,1,5,6,8,3,10 };
for (auto e : arr)
{
tree.Insert(e);
}
tree.InOrder();
if (tree.Find(10))
{
std::cout << "找到了!!" << std::endl;
}
else
{
std::cout << "没找到!!" << std::endl;
}
tree.Erase(3);
tree.InOrder();
tree.Erase(1);
tree.InOrder();
tree.Erase(9);
tree.InOrder();
tree.Erase(2);
tree.InOrder();
return 0;
}中序遍历,查找,删除总的运行结果:

三、用途
单一的二叉搜索树是没有意义的,我们无法控制节点的插入,会导致一个现象叫做"未平衡",也就是最坏的情况会存在单支二叉搜索树,这是时间复杂度就由O(logN)变为O(N),时间复杂度大大增加,所以使其保持"平衡"就非常重要,平衡二叉搜索树有一个新的名字叫做AVL树,引入更加复杂的修复(平衡操作),就变成了红黑树。
随后学习的STL容器map/set的底层都是红黑树。