二叉树的链式结构

迷途之人不知返2025-12-01 12:04

二叉树的链式结构

1、增删查改有意义吗？

我们之前在二叉树的简单介绍中讲过，对于非完全二叉树，使用链式结构实现。

我们还知道，实现这种二叉树，如果使用二叉链，那么（二叉树节点的）结构体成员包括数据 、左孩子 、右孩子。

c 复制代码 
typedef char BTDatatype;
typedef struct BinaryTreeNode
{
	BTDatatype val;
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
}BTNode;

经过之前的学习，我们很自然会类比迁移的觉得，我们在链式结构中，将实现增删查改 。但问题是，在一个非完全二叉树中，增删查改有意义吗？

我们来看这棵二叉树。

如果我们要插入一个节点，我们插在哪儿？ A 的左孩子上？ B 的左孩子上？ B 的右孩子上？

所以，在用链式结构实现的非完全二叉树上讨论节点的增删查改，没有意义。

而有意义的，是讨论一些遍历的方法。

2、前 / 中 / 后序遍历

2.1、概念简单介绍

  • 前序遍历 ：先遍历根节点，然后遍历左孩子结点，再遍历右孩子结点。又被称为先根遍历。
  • 中序遍历 ：先遍历左孩子结点，然后遍历根节点，再遍历右孩子结点。又被称为中根遍历。
  • 后序遍历 ：先遍历左孩子结点，然后遍历右孩子结点，再遍历根节点。又被称为后根遍历。

三个遍历方法，可以巧记为：
根左右 根左右 根左右 左根右 左根右 左根右 左右根 左右根 左右根

2.2、前序遍历

口诀为：根左右

如图：

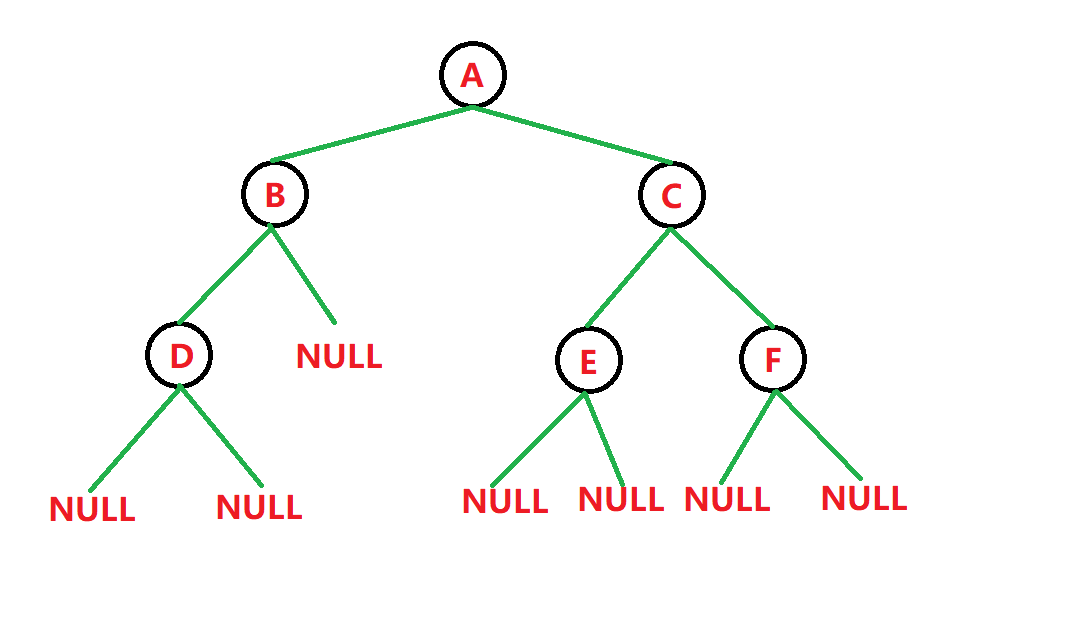
根据前序遍历的规则，我们从根节点开始，得到这样一个遍历顺序：
A − > B − > D − > N U L L − > N U L L − > N U L L − > C − > E − > N U L L − > N U L L − > F − > N U L L − > N U L L A->B->D->NULL->NULL->NULL->C->E->NULL->NULL->F->NULL->NULL A−>B−>D−>NULL−>NULL−>NULL−>C−>E−>NULL−>NULL−>F−>NULL−>NULL

是不是呢？代码实现一下：

c 复制代码 
void PreOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf(root->val);
	PreOrder(root->left);
	PreOrder(root->right);
}

会发现，完全符合。

代码中，我们用到了函数递归 。我们知道，每次调用一次函数，就会开辟一个函数栈帧；而函数调用结束后，函数栈帧就被销毁。

我们用红线代表函数开辟空间，用绿线代表函数结束归还空间，以图示来解释前序遍历的全过程：

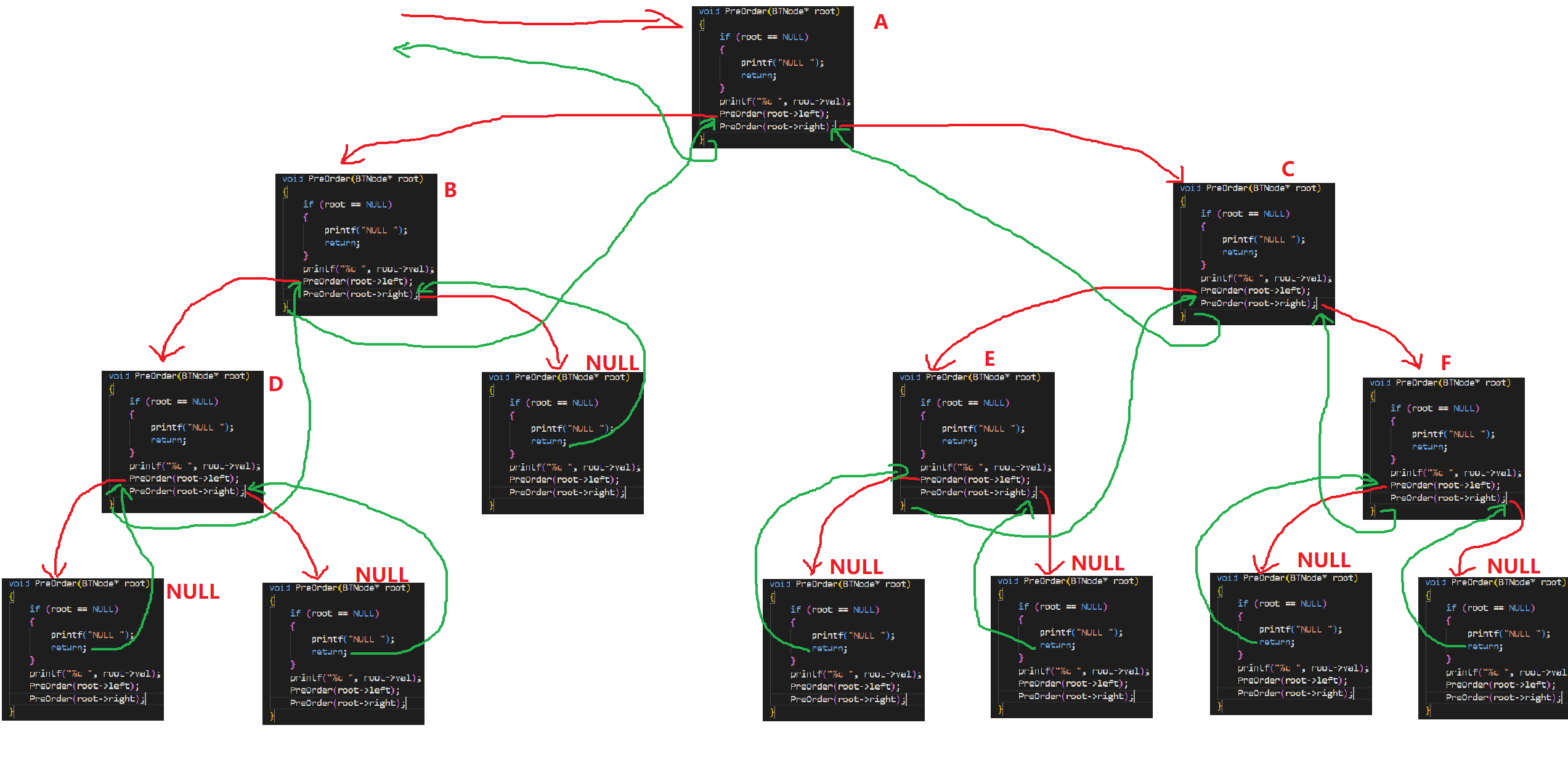
2.3、中序遍历

口诀为：前根后

c 复制代码 
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);
	printf(root->val);
	InOrder(root->right);
}

遍历顺序：
N U L L − > D − > N U L L − > B − > N U L L − > A − > N U L L − > E − > N U L L − > C − > N U L L − > F − > N U L L NULL-> D-> NULL-> B-> NULL-> A ->NULL-> E-> NULL-> C-> NULL-> F-> NULL NULL−>D−>NULL−>B−>NULL−>A−>NULL−>E−>NULL−>C−>NULL−>F−>NULL

根据上图和上面的代码，我们可以做出以下图示：

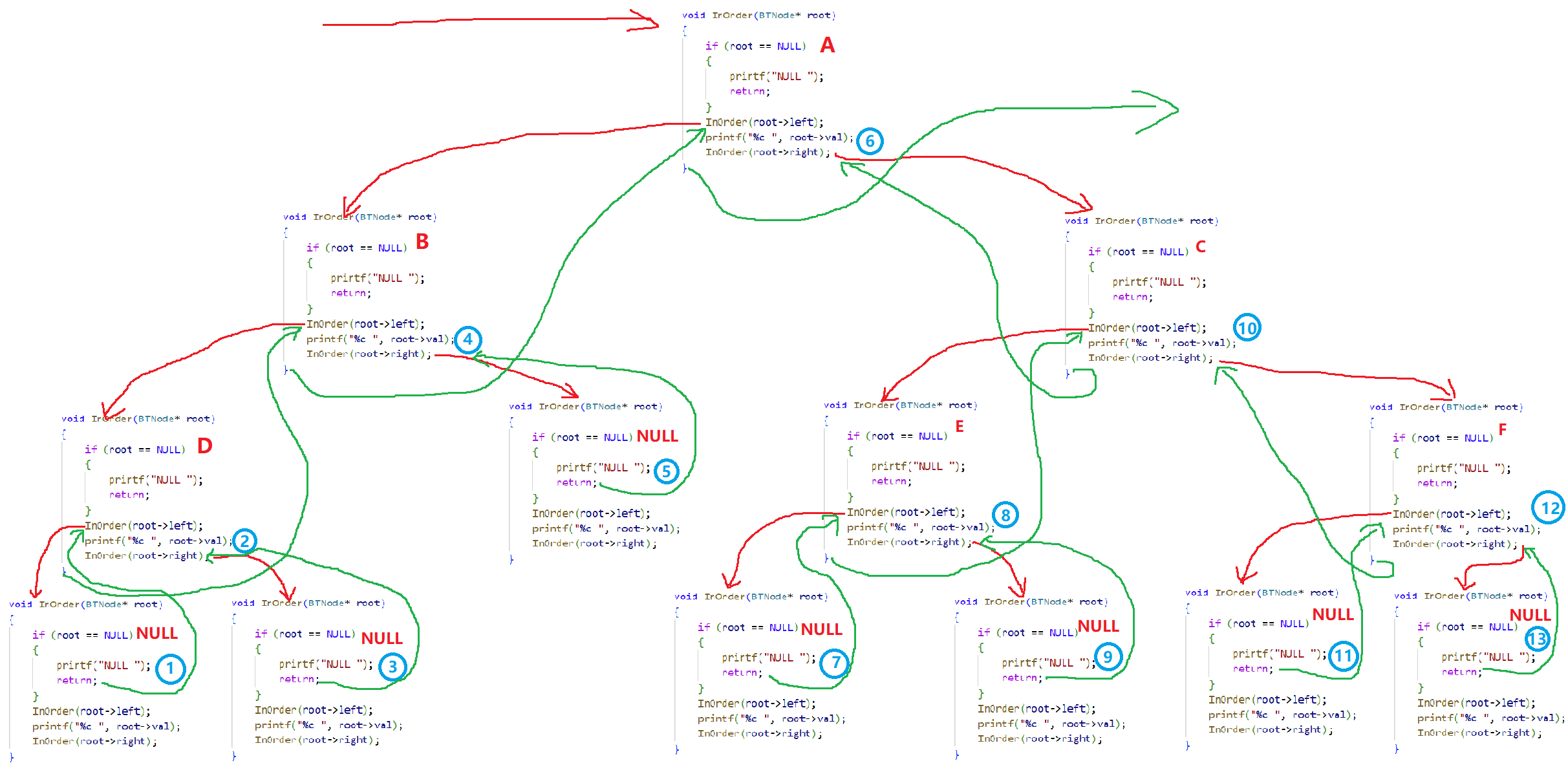
2.4、后序遍历

口诀为：前后根

c 复制代码 
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf(root->val);
}

遍历顺序：
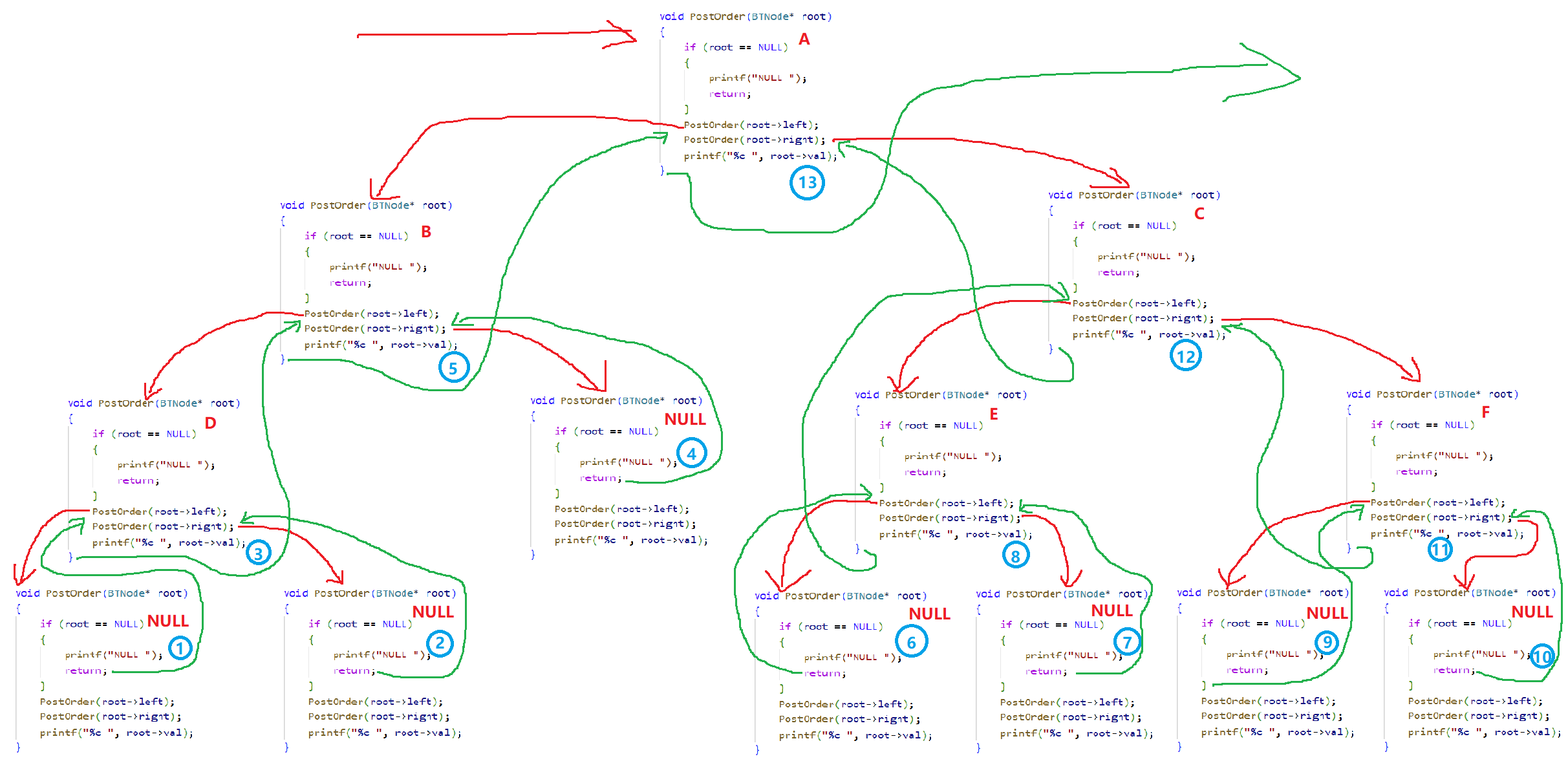
N U L L − > N U L L − > D − > N U L L − > B − > N U L L − > N U L L − > E − > N U L L − > N U L L − > F − > C − > A NULL-> NULL-> D-> NULL-> B-> NULL-> NULL-> E-> NULL-> NULL-> F-> C-> A NULL−>NULL−>D−>NULL−>B−>NULL−>NULL−>E−>NULL−>NULL−>F−>C−>A

根据上图和上面的代码，我们可以做出以下图示：

3、统计所有节点个数

如标题。

假如我们在函数里面直接创建一个计数器，用来统计节点的个数。

c 复制代码 
//统计所有结点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int size = 0;
	size++;
	BinaryTreeSize(root->left);
	BinaryTreeSize(root->right);

	return size;
}

我们不难知道，程序每次进入函数中时，size都会被修改成0，这样的处得到的答案一定是错的。

那么，将size定义为全局变量呢？（static和将size定义为全局变量的效果相同）

c 复制代码 
int size = 0;
//统计所有结点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	/*static int size = 0;*/
	size++;
	BinaryTreeSize(root->left);
	BinaryTreeSize(root->right);

	return size;
}

我们看到，此时产生了累加效果，意味着统计节点个数函数不能多次使用，也不行。

那我们往函数里添加一个参数，会怎样呢？

c 复制代码 
//统计所有结点个数
void BinaryTreeSize(BTNode* root, int* psize)
{
	if (root == NULL)
	{
		return;
	}
	(*psize)++;
	BinaryTreeSize(root->left, psize);
	BinaryTreeSize(root->right, psize);
}
c 复制代码 
void test()
{
    BTNode* root = CreatTree();

    // PreOrder(root);
    // printf("\n");
    // InOrder(root);
    // printf("\n");
    // PostOrder(root);

    int size = 0;
    BinaryTreeSize(root, &size);
    printf("%d\n", size);
    size = 0;
    BinaryTreeSize(root, &size);
    printf("%d\n", size);
}

这看似是解决了问题，但是比较麻烦，不仅要添加一个参数，还需要在测试文件中不断初始化size。

有没有更优的方法？递归。

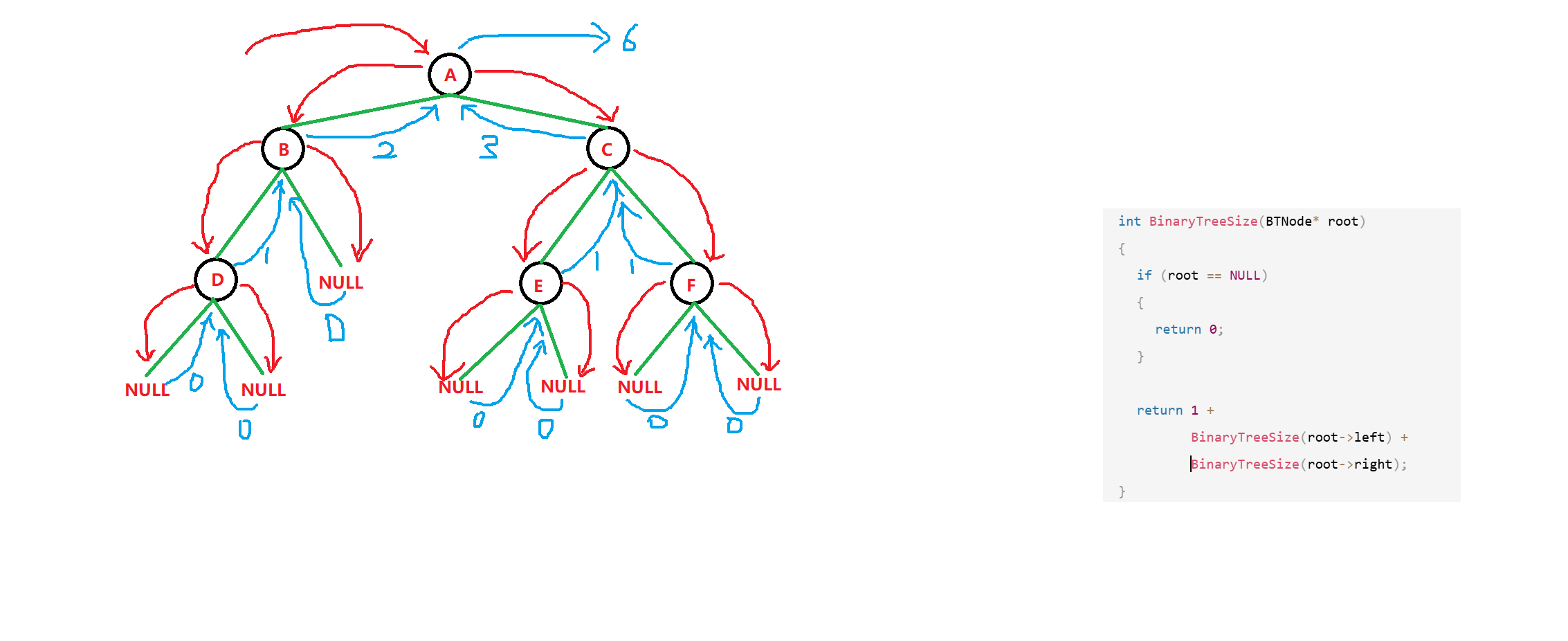
我们可以认为，节点个数可以分为左子树节点个数、右子树节点个数和父节点（1个）：
节点个数 = 左子树节点个数 + 右子树节点个数 + 父节点（ 1 ） 节点个数=左子树节点个数+右子树节点个数+父节点（1） 节点个数=左子树节点个数+右子树节点个数+父节点（1）

c 复制代码 
//统计所有结点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	
	return 1 + 
	       BinaryTreeSize(root->left) + 
	       BinaryTreeSize(root->right);
}

图示：

4、统计所有叶子节点的个数

什么是叶子节点？没有左、右孩子的节点（度为0）。

类比所有节点个数的求法，我们也可以认为：
叶子节点个数 = 左子树叶子节点个数 + 右子树叶子节点个数 叶子节点个数=左子树叶子节点个数+右子树叶子节点个数 叶子节点个数=左子树叶子节点个数+右子树叶子节点个数

同时，每一个节点的情况，无非三种：

  • 节点为空 。返回0
  • 节点没有孩子节点 。返回1
  • 节点有孩子节点 。继续递归到其左右孩子
c 复制代码 
//统计所有叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	//无非三种情况：当前节点为空，当前节点是叶子节点，当前节点不是叶子节点（有左/右孩子）
	if (root == NULL)
	{
		return 0;
	}
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	//前两种情况，每一种情况都要判断，所以不能用else if
	return BinaryTreeLeafSize(root->left) + 
	       BinaryTreeLeafSize(root->right);
}

5、统计第k层节点个数

第 k 层节点个数 = 左子树第 k 层节点个数 + 右子树第 k 层节点个数 第k层节点个数=左子树第k层节点个数+右子树第k层节点个数 第k层节点个数=左子树第k层节点个数+右子树第k层节点个数

我们不妨在参数中加入一个参数k，k代表要统计的层数为第k 层。每次向下一层，使k-1。当k==1，就来到了最底层。

所以还是存在三种情况。

c 复制代码 
//统计第k层所有节点个数
int BinaryTreeKFloorSize(BTNode* root, int k)
{
	//首先判断空节点
	if (root == NULL)
	{
		return 0;
	}
	//当k减到1，就来到了第k层，每一个函数栈帧对应一个节点，所以返回1
	if (k == 1)
	{
		return 1;
	}
	//到这里，就还没到第k层
	return BinaryTreeKFloorSize(root->left, k-1) + 
	       BinaryTreeKFloorSize(root->right, k-1);
}

6、计算二叉树深度

递推公式：
二叉树深度 = = 1 （父节点占一层） + m a x ( 左子树深度 , 右子树深度 ) 二叉树深度==1（父节点占一层）+max(左子树深度, 右子树深度) 二叉树深度==1（父节点占一层）+max(左子树深度,右子树深度)

c 复制代码 
//二叉树的深度/高度
int TreeDepth(BTNode* root)
{
	//递推公式：深度 = 1 + max(左子树深度, 右子树深度)
	if (root == NULL)
	{
		return 0;
	}
	//保存子树的深度
	int LeftDep = TreeDepth(root->left);
	int RightDep = TreeDepth(root->right);

	return 1 + (LeftDep > RightDep ? LeftDep : RightDep);
}

7、查找结点

可以通过递归进行" 遍历 "。

遇到的节点，无非三种情况：

  1. 为空。返回NULL
  2. 为要查找的节点，返回该节点
  3. 既不为空，又不是要查找的节点

对于第3点，可以先找其左子树，存下返回值，判断是否为空；如果都为空，再找右子树，重复操作；如果都没有，返回NULL。

c 复制代码 
//查找节点
BTNode* FindNode(BTNode* root, char str)
{
	//节点为空
	if (root == NULL)
	{
		return NULL;
	}
	//刚好为要找节点
	if (root->val == str)
	{
		return root; 
	}
	//既不是要找节点，又不为空
	//找左子树
	BTNode* LeftFind = FindNode(root->left, str);
	//判断
	if (LeftFind)
	{
		return LeftFind;
	}
	//走到这，左子树找完了，找右子树
	BTNode* RightFind = FindNode(root->right, str);
	//判断
	if (RightFind)
	{
		return RightFind;
	}
	//找到这，没有
	return NULL;
}

8、销毁二叉树

销毁二叉树的顺序，应该是：左、右、根。

如果不按照这个顺序来，那么将会找不到根节点的子树。

当然，节点为空，不能释放。

c 复制代码 
//销毁二叉树
void TreeDestroy(BTNode** proot)
{
	//会改变二叉树，需要二级指针
	//为空，不需要销毁
	if (*proot == NULL)
	{
		return;
	}
	//不为空，销毁顺序：左右根
	TreeDestroy(&((*proot)->left));
	TreeDestroy(&((*proot)->right));
	free(*proot);
	*proot = NULL;
}

9、层序遍历

我们前面学习的前、中、后序遍历，属于深度优先遍历。

而现在要学习的层序遍历，则属于广度优先遍历。

比如还是拿这个二叉树举例：

这个二叉树，层序遍历的结果，当然是：
A − > B − > C − > D − > E − > F A->B->C->D->E->F A−>B−>C−>D−>E−>F

要实现层序遍历，我们需要借助之前学习过的数据结构------队列。

思路：

  • 创建队列，入二叉树根节点，使队列不为空
  • 以队列不为空的条件建立while循环，执行下面操作：
    • 取（当前）队头，打印，出队头
    • （当队列不为空时）按顺序插入对头的左、右孩子（左、右孩子不能为空）

注意到，队头取出时一般会存下，所以入左右孩子操作与打印出队头操作没有先后顺序之分。但我们最好使用上面的顺序，便于理解。

我们需要在层序遍历的函数中，创建队列，那么，我们不仅需要将队列的实现（头文件、原文件）拷贝到当前项目下，还要在BinaryTree.c的顶上，加上头文件"Queue.h"。

那么这时，我们在队列中存放的每一个数据，就不是字符了，而是二叉树的节点：

c 复制代码 
typedef struct BinaryTreeNode* QueueDataType;

其中，我们没有在Queue.h文件中，加入头文件"BinaryTree.h"头文件，就定义了结构体指针类型struct BinaryTreeNode*。这样做是可以的，因为这样就等于声明了有这么样一个结构体，同时用另一个名称重命名这个结构体。

代码演示（队列的实现就不重复说明了）：

c 复制代码 
//层序遍历
void LevelOder(BTNode* root)
{
	//创建队列
	Queue q;
	//初始化
	QueueInit(&q);
	//入根节点
	QueuePush(&q, root);
	//循环
	while (!QueueEmpty(&q))
	{
		// //取队顶
		// BTNode* front = QueueHead(&q);
		// //打印
		// printf("%c ", front->val);
		// //出队列
		// QueuePop(&q);
		// //入左右孩子
		// if (front->left)
		// {
		// 	QueuePush(&q, front->left);
		// }
		// if (front->right)
		// {
		// 	QueuePush(&q, front->right);
		// }
		//取队顶
		BTNode* front = QueueHead(&q);
		//入左右孩子
		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}
		//打印
		printf("%c ", front->val);
		//出队列
		QueuePop(&q);

	}
}

10、判断完全二叉树

完全二叉树有两个性质：

  • 除最底层外所有层，节点个数达到最大（符合满二叉树特点）
  • 最底层不一定达到最大，但是从左到右排列

判断是否完全二叉树，方法与层序遍历类似：

  1. 创建队列，首先入根节点。
  2. 当队列不为空，进入循环，取队头，存下队头，出队头
  3. 如果存下的队头为空，结束循环；否则，入左、右孩子
  4. 结束循环后，继续循环，取队头，判断是否存的是非空节点。如果有非空节点，那就不是完全二叉树；如果全是空节点，那么是完全二叉树

如图：

非完全二叉树：

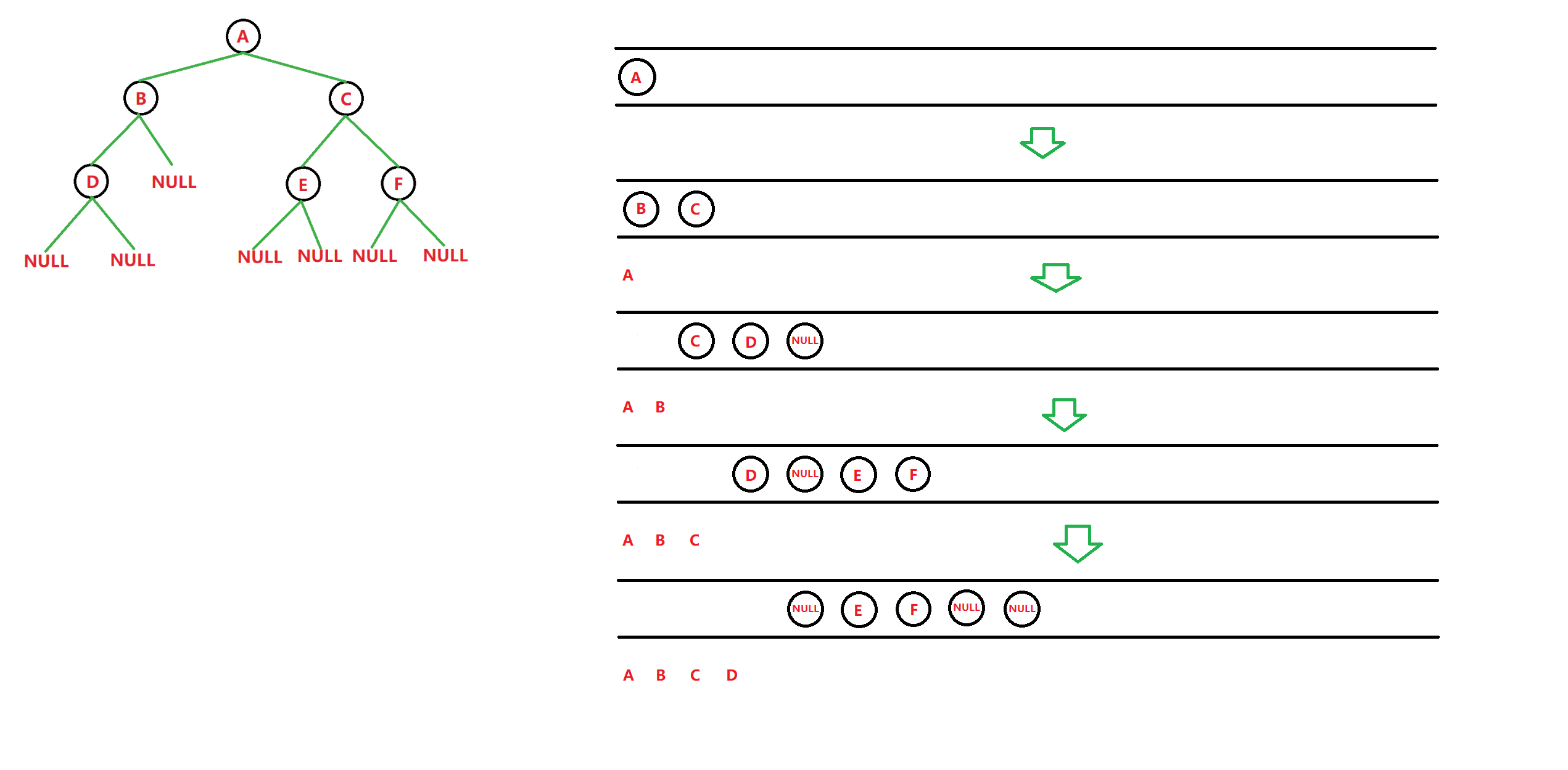
完全二叉树：

代码演示：

c 复制代码 
//判断完全二叉树
bool IsComplete(BTNode* root)
{
	//创建队列
	Queue q;
	//初始化
	QueueInit(&q);
	//入根节点
	QueuePush(&q, root);
	//循环
	while (!QueueEmpty(&q))
	{
		//取队顶，接受
		BTNode* front = QueueHead(&q);
		//出队顶
		QueuePop(&q);
		//判断
		if (front == NULL)
		{
			break;
		}
		//直接入左右孩子
		QueuePush(&q, front->left);//不只是根节点
		QueuePush(&q, front->right);
	}
	//再循环
	while (!QueueEmpty(&q))
	{
		//取队顶，接受
		BTNode* front = QueueHead(&q);
		//出队顶
		QueuePop(&q);//最好取完就出
		//判断
		if (front)
		{
			//销毁队列
			QueueDestroy(&q);//也要销毁
			return false;
		}

	}
	return true;

	//销毁队列
	QueueDestroy(&q);
}

最后附上完整代码：链式结构

相关推荐
不会c嘎嘎1 小时前
【数据结构】红黑树详解：从原理到C++实现
开发语言·数据结构
吃着火锅x唱着歌1 小时前
LeetCode 2364.统计坏数对的数目
数据结构·算法·leetcode
kyle~1 小时前
数据结构---堆（Heap）
服务器·开发语言·数据结构·c++
带土11 小时前
13. 某马数据结构整理（1）
数据结构
Kuo-Teng1 小时前
Mastering High-Concurrency Data Processing: A Deep Dive into BufferTrigger
java·数据结构
秋深枫叶红2 小时前
嵌入式第二十三篇——数据结构基本概念
linux·数据结构·学习·算法
Zsy_0510032 小时前
【数据结构】二叉树介绍及C语言代码实现
c语言·数据结构·算法
小白程序员成长日记2 小时前
力扣每日一题 2025.11.30
数据结构·算法·leetcode
爱学习的小邓同学3 小时前
数据结构 --- 二叉搜索树
数据结构·c++
热门推荐
01GitHub 镜像站点02BongoCat - 跨平台键盘猫动画工具03UV安装并设置国内源04Linux下V2Ray安装配置指南05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连0746个Nano-banana 精选提示词，持续更新中08“我的电脑”图标没了怎么办 4种方法找回09全球最强模型Grok4，国内已可免费使用！（附教程）10Labelme从安装到标注：零基础完整指南