LeetCode 3623.统计梯形的数目 I

给你一个二维整数数组 points，其中 points[i] = [xi, yi] 表示第 i 个点在笛卡尔平面上的坐标。

水平梯形是一种凸四边形，具有至少一对水平边（即平行于 x 轴的边）。两条直线平行当且仅当它们的斜率相同。

返回可以从 points 中任意选择四个不同点组成的水平梯形数量。

由于答案可能非常大，请返回结果对 10 9 ^9 9 + 7 取余数后的值。

示例 1：

输入： points = [[1,0],[2,0],[3,0],[2,2],[3,2]]

输出： 3

解释：

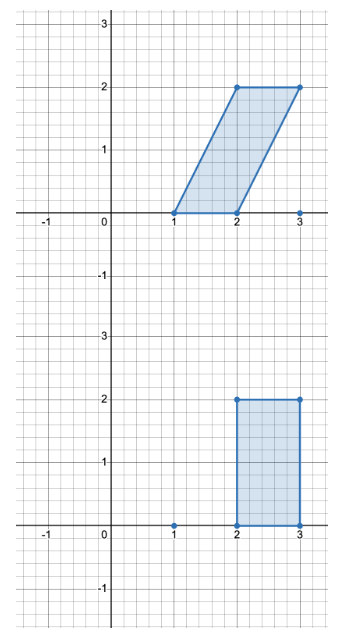
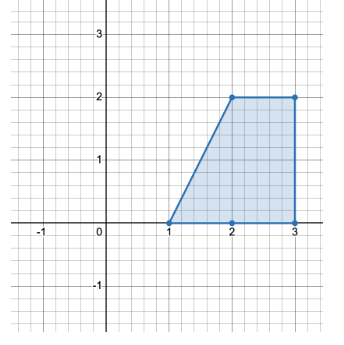
有三种不同方式选择四个点组成一个水平梯形：

使用点 [1,0]、[2,0]、[3,2] 和 [2,2]。

使用点 [2,0]、[3,0]、[3,2] 和 [2,2]。

使用点 [1,0]、[3,0]、[3,2] 和 [2,2]。

示例 2：

输入： points = [[0,0],[1,0],[0,1],[2,1]]

输出： 1

解释：

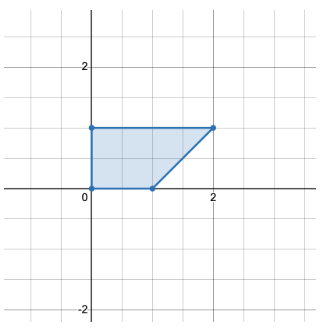
只有一种方式可以组成一个水平梯形。

提示：

4 <= points.length <= 10 5 ^5 5

--10 8 ^8 8 <= xi, yi <= 10 8 ^8 8

所有点两两不同。

我们可以先把每行有几个点保存到一个哈希表中，然后遍历哈希表，遍历每一行时，计算出当前行中任取两点有几种取法c，然后将c与之前遍历到的行中任取两点的取法之和相乘：

cpp 复制代码

class Solution {
public:
    int countTrapezoids(vector<vector<int>>& points) {
        unordered_map<int, int> cnt;
        for (vector<int> &point : points) {
            ++cnt[point[1]];
        }

        long long ans = 0;
        long long s = 0;
        for (pair<const int, int> oneCnt : cnt) {
            int num = oneCnt.second;
            long long c = (long long)num * (num - 1) / 2;
            
            ans += c * s;
            s += c;
        }

        return ans % (int)(1e9 + 7);
    }
};

如果points中有n个点，点所在的行的范围为m，则此算法时间复杂度为O(n)，空间复杂度为O(m)。