力扣133.克隆图

一、问题分析

1. 问题描述

给定无向连通图中一个节点的引用，要求返回该图的深拷贝 （克隆）。图中每个节点包含值val和邻居列表neighbors，需保证：

• 新图与原图结构完全一致，但所有节点都是新创建的（内存独立）；
• 无向图的双向引用需正确复制（如节点 A 的邻居包含 B，则节点 B 的邻居也需包含 A 的克隆节点）；
• 避免重复创建节点（防止循环引用导致死循环或重复节点）。

2. 核心难点

• 循环引用处理：无向图中节点间的双向引用（如 1↔2），直接递归 / 遍历会重复访问节点；
• 深拷贝保证：必须为每个节点创建新实例，且邻居列表指向克隆节点而非原节点；
• 连通性保证：原图是连通的，需遍历所有可达节点并完成克隆。

二、题目解析

1. 输入输出定义

• 输入：无向连通图的起始节点（值为 1）；
• 输出：克隆图的起始节点（新内存地址，结构与原图一致）。

2. 示例理解

以邻接列表[[2,4],[1,3],[2,4],[1,3]]为例：

• 节点 1 的邻居是 2、4；
• 节点 2 的邻居是 1、3；
• 节点 3 的邻居是 2、4；
• 节点 4 的邻居是 1、3；克隆后需生成新的 4 个节点，邻居关系与原图完全一致。

三、算法分析

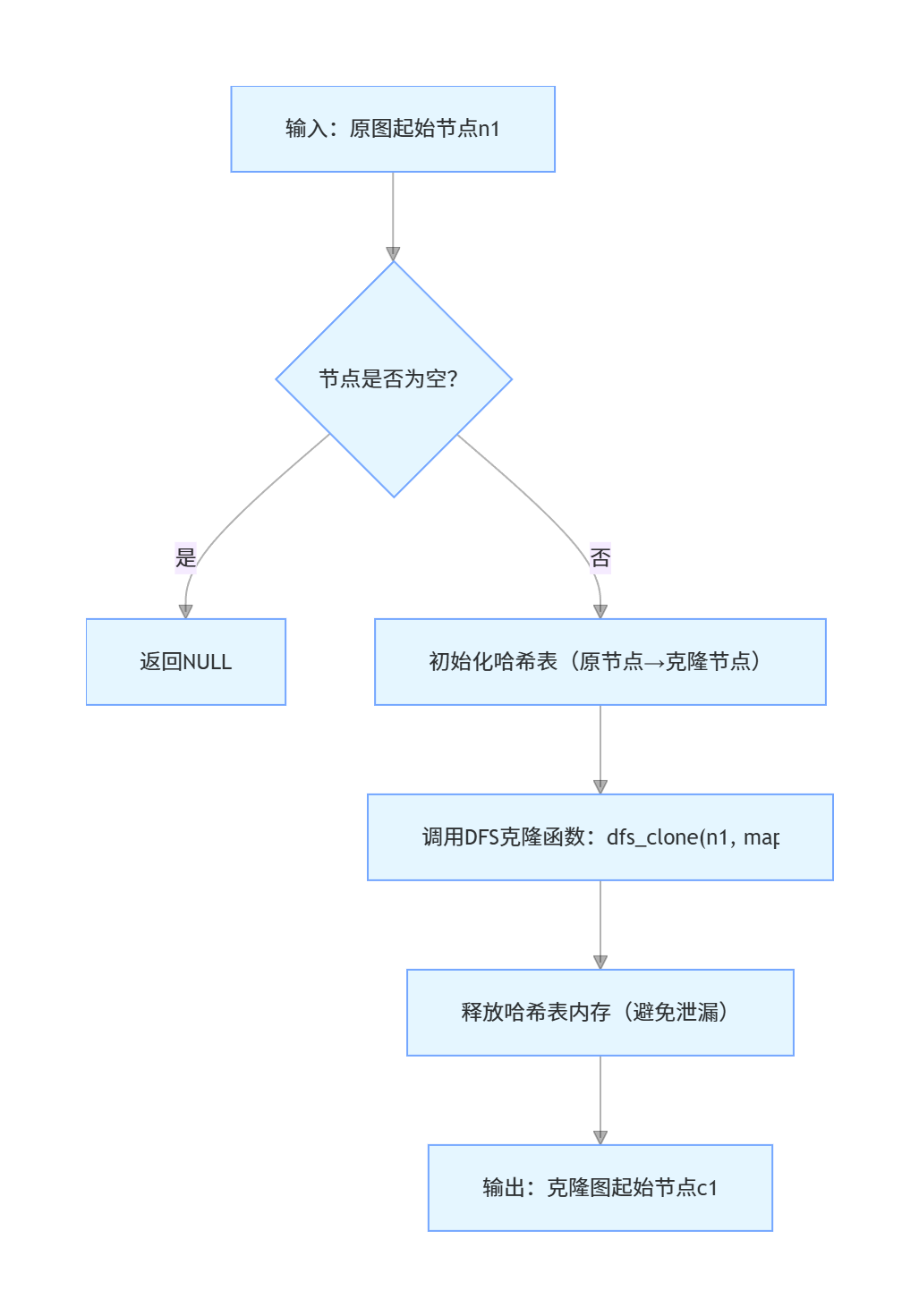
采用深度优先搜索（DFS）+ 哈希表（映射表） 实现，核心逻辑：

1. 哈希表记录映射关系：键为原节点指针，值为克隆节点指针，避免重复创建；
2. DFS 遍历 + 克隆 ：
   • 若当前节点已克隆（哈希表中存在），直接返回克隆节点；
   • 若未克隆，创建新节点，存入哈希表；
   • 递归克隆当前节点的所有邻居，添加到新节点的邻居列表；
3. 无向图处理：递归过程中自动处理双向引用（如克隆 1 的邻居 2 时，会同步克隆 2 的邻居 1）。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

// 图节点定义
struct Node {
    int val;
    int numNeighbors;
    struct Node** neighbors;
};

// 哈希表节点定义（用于存储原节点→克隆节点的映射）
typedef struct HashNode {
    struct Node* key;        // 原节点指针
    struct Node* value;      // 克隆节点指针
    struct HashNode* next;   // 链表下一个节点
} HashNode;

// 哈希表定义
#define HASH_SIZE 1009       // 哈希表大小（质数，减少冲突）
typedef struct {
    HashNode* table[HASH_SIZE];
} HashMap;

// 哈希函数：将指针转换为整数，取模
static int hash_func(struct Node* key) {
    return (unsigned long)key % HASH_SIZE;
}

// 初始化哈希表
HashMap* hash_map_init() {
    HashMap* map = (HashMap*)malloc(sizeof(HashMap));
    memset(map->table, 0, sizeof(map->table));
    return map;
}

// 哈希表存入键值对
void hash_map_put(HashMap* map, struct Node* key, struct Node* value) {
    int idx = hash_func(key);
    HashNode* node = (HashNode*)malloc(sizeof(HashNode));
    node->key = key;
    node->value = value;
    node->next = map->table[idx];  // 头插法
    map->table[idx] = node;
}

// 哈希表查询键对应的值
struct Node* hash_map_get(HashMap* map, struct Node* key) {
    int idx = hash_func(key);
    HashNode* cur = map->table[idx];
    while (cur) {
        if (cur->key == key) {
            return cur->value;
        }
        cur = cur->next;
    }
    return NULL;
}

// 释放哈希表内存
void hash_map_free(HashMap* map) {
    for (int i = 0; i < HASH_SIZE; i++) {
        HashNode* cur = map->table[i];
        while (cur) {
            HashNode* tmp = cur;
            cur = cur->next;
            free(tmp);
        }
    }
    free(map);
}

// 创建新节点（初始化值和邻居数组）
struct Node* create_node(int val) {
    struct Node* node = (struct Node*)malloc(sizeof(struct Node));
    node->val = val;
    node->numNeighbors = 0;
    node->neighbors = NULL;
    return node;
}

// 递归克隆节点（核心DFS逻辑）
struct Node* dfs_clone(struct Node* node, HashMap* map) {
    // 边界条件：节点为空
    if (node == NULL) return NULL;
    
    // 已克隆过，直接返回
    struct Node* cloned = hash_map_get(map, node);
    if (cloned != NULL) return cloned;
    
    // 创建当前节点的克隆
    cloned = create_node(node->val);
    hash_map_put(map, node, cloned);  // 先存入映射，避免循环引用
    
    // 克隆所有邻居
    cloned->numNeighbors = node->numNeighbors;
    if (node->numNeighbors > 0) {
        cloned->neighbors = (struct Node**)malloc(sizeof(struct Node*) * node->numNeighbors);
        for (int i = 0; i < node->numNeighbors; i++) {
            // 递归克隆邻居节点
            cloned->neighbors[i] = dfs_clone(node->neighbors[i], map);
        }
    }
    
    return cloned;
}

// 克隆图主函数
struct Node* cloneGraph(struct Node* node) {
    // 初始化哈希表
    HashMap* map = hash_map_init();
    // DFS克隆
    struct Node* res = dfs_clone(node, map);
    // 释放哈希表（避免内存泄漏）
    hash_map_free(map);
    return res;
}

// 辅助函数：释放图的内存（测试用）
void free_graph(struct Node* node, HashMap* visited) {
    if (node == NULL) return;
    // 避免重复释放
    if (hash_map_get(visited, node) != NULL) return;
    hash_map_put(visited, node, node);
    
    // 释放邻居数组
    if (node->neighbors != NULL) {
        for (int i = 0; i < node->numNeighbors; i++) {
            free_graph(node->neighbors[i], visited);
        }
        free(node->neighbors);
    }
    free(node);
}

int main() {
    // 构建原图：1→2、4；2→1、3；3→2、4；4→1、3
    struct Node* n1 = create_node(1);
    struct Node* n2 = create_node(2);
    struct Node* n3 = create_node(3);
    struct Node* n4 = create_node(4);
    
    n1->numNeighbors = 2;
    n1->neighbors = (struct Node**)malloc(sizeof(struct Node*) * 2);
    n1->neighbors[0] = n2;
    n1->neighbors[1] = n4;
    
    n2->numNeighbors = 2;
    n2->neighbors = (struct Node**)malloc(sizeof(struct Node*) * 2);
    n2->neighbors[0] = n1;
    n2->neighbors[1] = n3;
    
    n3->numNeighbors = 2;
    n3->neighbors = (struct Node**)malloc(sizeof(struct Node*) * 2);
    n3->neighbors[0] = n2;
    n3->neighbors[1] = n4;
    
    n4->numNeighbors = 2;
    n4->neighbors = (struct Node**)malloc(sizeof(struct Node*) * 2);
    n4->neighbors[0] = n1;
    n4->neighbors[1] = n3;
    
    // 克隆图
    struct Node* cloned = cloneGraph(n1);
    
    // 验证克隆结果（输出克隆节点1的邻居值）
    printf("克隆节点1的邻居值：");
    for (int i = 0; i < cloned->numNeighbors; i++) {
        printf("%d ", cloned->neighbors[i]->val);
    }
    printf("\n");  // 应输出：2 4
    
    // 释放原图和克隆图内存
    HashMap* visited1 = hash_map_init();
    free_graph(n1, visited1);
    hash_map_free(visited1);
    
    HashMap* visited2 = hash_map_init();
    free_graph(cloned, visited2);
    hash_map_free(visited2);
    
    return 0;
}

四、复杂度分析

1. 时间复杂度：O (N + E)

• N：图中节点数量；
• E：图中边的数量；
• 每个节点仅被克隆一次（哈希表去重），每条边仅被处理两次（无向图双向引用），总操作数为 O (N + E)。

2. 空间复杂度：O (N)

• 哈希表存储 N 个节点的映射，空间 O (N)；
• DFS 递归栈深度最坏为 O (N)（如链式图）；
• 总空间复杂度为 O (N)。