知识点:
- 方差筛选
- 皮尔逊相关系数筛选
- lasso 筛选
- 树模型重要性
- shap 重要性
- 递归特征消除 REF
方差筛选
我们今天从最基础的概念开始讲方差筛选,不用怕听不懂,我会用大白话 + 小例子一步步说清楚~
第一步:先搞懂「方差」是啥?
方差是用来衡量一组数据波动大小的指标。简单说:
- 如果一组数据里的数都差不多(比如全班同学的「性别」:要么 0 要么 1,波动小),方差就小;
- 如果一组数据里的数差别很大(比如全班同学的「身高」:150cm 到 190cm 都有,波动大),方差就大。
举个具体例子:
- 数据 A:[1,1,1,1] → 所有数都一样,波动为 0,方差 = 0;
- 数据 B:[1,2,3,4] → 数差别大,波动大,方差≈1.25;
第二步:方差筛选是干啥的?
我们做数据分析 / 机器学习时,会有很多「特征」(比如分析学生成绩时,特征有:性别、年龄、每天学习时长、是否每天吃早饭...)。
如果某个特征的方差特别小 (比如「是否每天呼吸」:所有人都是 1,方差 = 0),这个特征对分析结果没任何帮助(因为它不会区分不同的样本)。
方差筛选的核心就是:把方差太小的、没信息量的特征删掉,只留下方差大的、能体现差异的特征。
第三步:用 Python 实操方差筛选(超简单!)
我们用最基础的代码演示,你跟着敲就行~
1. 先准备工具(导入库)
python
# pandas用来装数据,VarianceThreshold是专门做方差筛选的工具
import pandas as pd
from sklearn.feature_selection import VarianceThreshold2. 造一组简单数据(模拟真实特征)
假设我们有 4 个特征:
- 特征 1:性别(0 = 女,1 = 男)
- 特征 2:年龄(18-22 岁)
- 特征 3:是否每天喝水(几乎所有人都喝,所以大部分是 1)
- 特征 4:每月零花钱(500-2000 元)
python
# 造数据:每行是一个学生,每列是一个特征
data = pd.DataFrame({
"性别": [0,1,0,1,0],
"年龄": [18,19,20,21,22],
"是否每天喝水": [1,1,1,1,0], # 方差很小(只有1个0)
"每月零花钱": [800,1500,1000,2000,1200]
})
print("原始数据:")
print(data)3. 用方差筛选器过滤特征
我们设定一个「方差阈值」(比如 0.1),只保留方差≥0.1 的特征:
python
# 1. 创建筛选器,设置阈值=0.1
selector = VarianceThreshold(threshold=0.1)
# 2. 用筛选器处理数据(注意:sklearn工具只认数值,这里数据都是数值,直接用)
new_data = selector.fit_transform(data)
# 3. 看筛选后剩下的特征是哪些
# 先拿到被保留的特征索引
keep_cols = selector.get_support(indices=True)
# 再从原数据里取这些列的名字
keep_feature_names = data.columns[keep_cols]
print("\n筛选后保留的特征:", keep_feature_names.tolist())
print("筛选后的数据:")
print(new_data)运行结果解释
- 原始特征里,「是否每天喝水」的方差≈0.04(小于 0.1),被删掉了;
- 剩下的特征是:性别、年龄、每月零花钱(它们的方差都≥0.1);
总结一下
方差筛选就是「去掉没波动、没信息量的特征」,步骤就 3 个:
- 选方差阈值(比如 0.1、0.05,根据数据调整);
- 用
VarianceThreshold筛选; - 保留筛选后的特征。
是不是很简单?你可以自己改改阈值(比如改成 0.05),看看结果会变吗~ 😊
方差筛选是一种简单而有效的特征筛选方法。它的核心逻辑是:特征的方差反映了数据的变化程度,方差很小的特征几乎没有变化,对模型的预测帮助不大。比如,一个特征的值在所有样本中几乎都一样(方差接近0),那么它对区分不同类别或预测结果几乎没有贡献。因此,方差筛选会设定一个方差阈值,剔除方差低于这个阈值的特征,保留那些变化较大的特征,从而减少特征数量,提高模型效率。
这种方法特别适合处理高维数据,能快速去掉不重要的特征,但它不考虑特征与目标变量之间的关系,可能会误删一些低方差但有意义的特征。
用代码实现方差筛选的具体步骤是什么?
我们把用代码实现方差筛选的步骤拆成5 个具体、可操作的环节,每个环节配代码 + 解释,你跟着一步步来就行~
步骤 1:导入必要的工具库
首先要导入处理数据的pandas(像 Excel 一样管理数据)和专门做方差筛选的VarianceThreshold(来自 sklearn 库):
python
# 导入pandas,用于存储和查看数据
import pandas as pd
# 导入方差筛选工具VarianceThreshold
from sklearn.feature_selection import VarianceThreshold步骤 2:准备数据(数值型特征)
方差筛选只针对数值型数据(比如价格、年龄),先构造或导入你的数据。这里用简单例子演示:
python
# 构造示例数据:每行是一个样本(比如用户),每列是特征
data = pd.DataFrame({
"年龄": [20, 25, 30, 35, 40], # 波动大
"消费金额": [100, 200, 150, 300, 250], # 波动中等
"是否有手机": [1, 1, 1, 1, 0], # 波动小
"是否呼吸": [1, 1, 1, 1, 1] # 无波动(方差=0)
})
# 打印原始数据,看看长什么样
print("原始数据:")
print(data)步骤 3:创建方差筛选器(设置阈值)
VarianceThreshold的核心参数是threshold(方差阈值):方差≥阈值的特征保留,< 阈值的删除 。比如设置阈值为0.1(你可以根据数据调整):
python
# 创建筛选器,指定方差阈值为0.1
selector = VarianceThreshold(threshold=0.1)步骤 4:执行筛选(拟合 + 转换数据)
用fit_transform()方法让筛选器 "学习" 数据的方差,并自动删掉方差太小的特征:
python
# 对数据执行筛选:fit计算方差,transform筛选特征
filtered_data = selector.fit_transform(data)步骤 5:查看筛选结果(保留的特征 + 数据)
筛选后的数据是数组形式,需要关联回原特征名,才能知道哪些特征被保留了:
python
# 1. 获取被保留特征的列索引(比如第0列、第1列被保留)
keep_indices = selector.get_support(indices=True)
# 2. 根据索引获取原数据的特征名
keep_features = data.columns[keep_indices]
# 3. 打印结果
print("\n保留的特征:", keep_features.tolist())
print("筛选后的数据:")
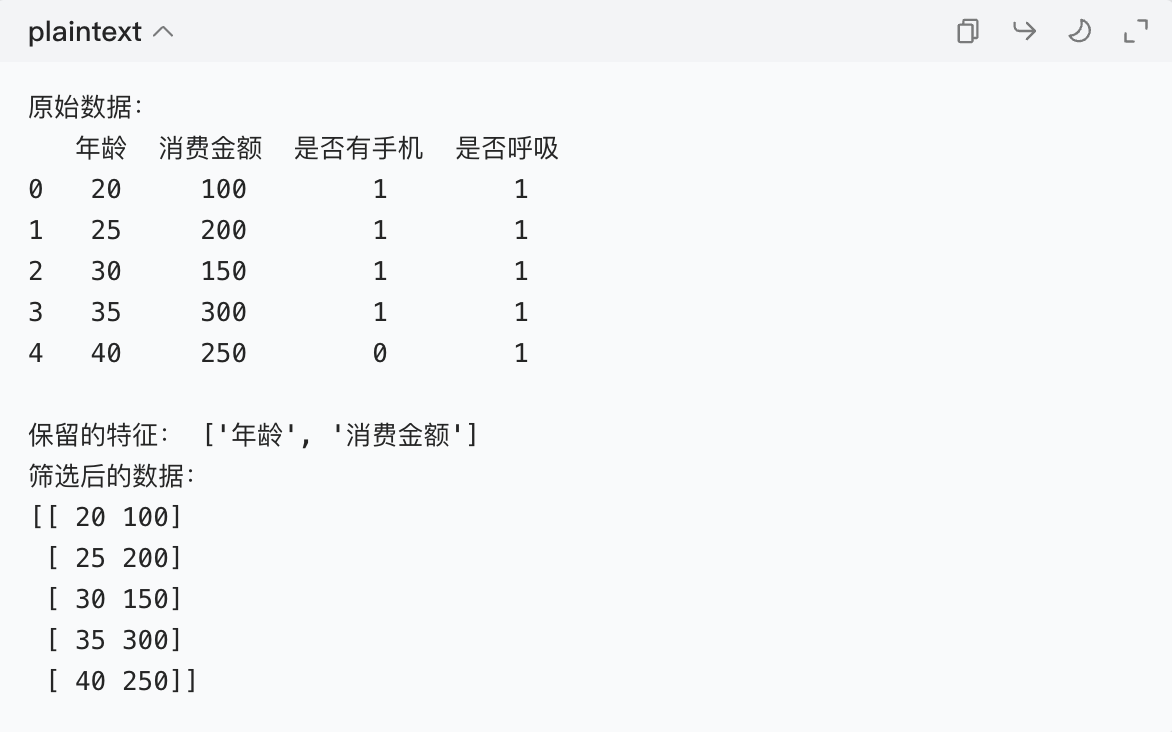
print(filtered_data)完整代码 + 运行结果
把上面的代码拼起来,运行后会看到:
额外:如果数据是 CSV 文件(真实场景)
如果你的数据存在 CSV 文件里(比如data.csv),只需把步骤 2 改成:
python
# 从CSV文件读取数据(确保特征列都是数值型)
data = pd.read_csv("data.csv")总结关键步骤
- 导入库 → 2. 准备 / 读取数值型数据 → 3. 创建筛选器(设阈值) → 4.
fit_transform()筛选 → 5. 查看保留的特征和数据这就是代码实现方差筛选的完整流程,你可以改阈值(比如0.05)或换数据试试,很快就能掌握~
如何判断数据集中的特征是数值型还是非数值型?
判断数据集中特征是数值型还是非数值型,其实很简单 ------先看特征的「用途」和「表现形式」,再用 Python 工具验证,我用大白话 + 代码实操一步步教你~
一、先搞懂:数值型 vs 非数值型的本质区别
| 类型 | 特点(大白话) | 例子 |
|---|---|---|
| 数值型 | 能做数学计算(加减乘除、算均值 / 方差) | 年龄(20/25)、价格(50.5)、销量(100) |
| 非数值型 | 用来分类 / 描述,不能做数学计算(就算是数字也不行) | 性别(男 / 女)、颜色(红 / 蓝)、邮编(100000,只是编号) |
二、方法 1:「肉眼观察」手动判断(新手先学这个)
直接看特征的数据内容 和用途:
- 如果特征是「可量化的指标」(比如身高、收入、分数)→ 数值型;
- 如果特征是「分类 / 描述性标签」(比如职业、学历、品牌)→ 非数值型;
⚠️ 注意:有些看起来是数字的特征,其实是非数值型!比如:
- 邮编(100000、200000):只是编号,不能算 "100000+200000=300000";
- 身份证号(110xxxx):只是标识,无数学意义;
- 等级(1 = 差、2 = 中、3 = 好):虽然是数字,但本质是分类,也算 "半数值型"(有序分类)。
三、方法 2:用 Python 代码「自动判断」(实际工作常用)
用pandas库查看特征的数据类型(dtype),这是最准确的方式:
步骤 1:先构造一个混合类型的数据集(演示用)
python
import pandas as pd
data = pd.DataFrame({
"年龄": [20, 25, 30], # 数值型(整数int)
"体重": [55.5, 60.2, 65.0], # 数值型(浮点数float)
"性别": ["男", "女", "男"], # 非数值型(字符串object)
"职业": ["学生", "教师", "程序员"], # 非数值型(字符串object)
"邮编": ["100000", "200000", "300000"], # 非数值型(字符串,就算存成数字也是分类)
"满意度": [1, 2, 3] # 有序分类(算半数值型)
})步骤 2:用info()查看所有特征的类型
info()会列出每列的 ** 数据类型(dtype)** 和非空值数量:
python
print("数据集的类型信息:")
data.info()输出结果解读:
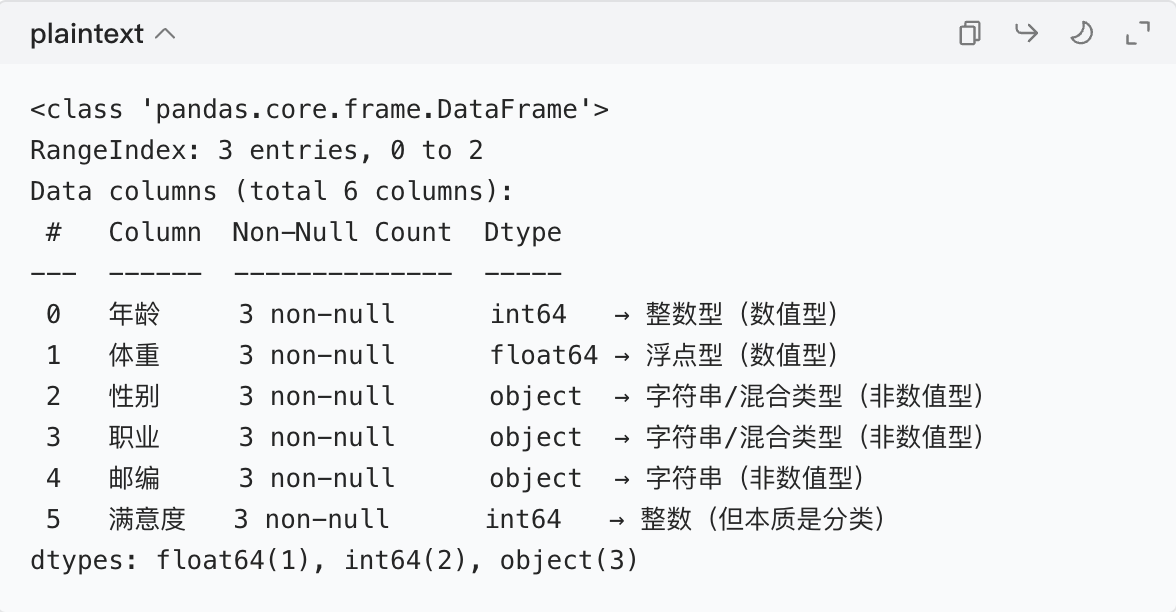
步骤 3:用dtypes只看类型(更简洁)
python
print("\n各特征的类型:")
print(data.dtypes)四、关键总结:Python 里的类型对应关系
| pandas 中的 dtype | 特征类型 | 例子 |
|---|---|---|
int64/float64 |
数值型 | 年龄、价格 |
object |
非数值型(字符串 / 分类) | 性别、职业 |
category |
非数值型(类别型) | 手动指定的分类 |
五、小技巧:处理 "伪装成数字的非数值型"
比如邮编如果被存成int64(数字),但实际是分类:
python
# 把邮编从数字转成字符串(非数值型)
data["邮编"] = data["邮编"].astype(str)
print(data.dtypes) # 邮编变成object类型这样你就能轻松判断啦!记住:看用途 + 看 dtype,两者结合就不会错~ 😊
皮尔逊相关系数筛选
皮尔逊相关系数筛选是一种基于特征与目标变量之间相关性的特征选择方法。它的核心逻辑是:计算每个特征与目标变量之间的相关系数(范围在-1到1之间,值越大表示正相关越强,值越小表示负相关越强,接近0表示几乎无关),然后根据相关系数的绝对值大小,选择与目标变量相关性较高的特征,剔除相关性较低的特征。这种方法适用于目标变量是连续型的情况(如果是分类问题,可以先对目标变量编码)。通过皮尔逊相关系数筛选,我们可以保留那些对预测目标最有帮助的特征,减少无关或冗余特征的干扰。
皮尔逊相关系数筛选法是一种基于变量相关性的经典特征选择技术,常用于处理目标变量为连续型的场景。若面对分类问题,通常需要先对目标变量进行编码处理,将其转化为数值型数据后再开展分析。
我们今天从基础概念 到代码实操 ,一步步讲清楚「皮尔逊相关系数筛选」------ 它是用来找变量之间线性关系的工具,筛选的核心是保留和目标变量相关性高的特征,剔除冗余的高度相关特征~
第一步:先搞懂「皮尔逊相关系数」是啥?
皮尔逊相关系数(Pearson Correlation Coefficient)是衡量两个数值型变量之间线性相关程度 的指标,结果用 r 表示:
- r 的范围:-1 ≤ r ≤ 1
- 含义 :
- r = 1:完全正相关(一个变量涨,另一个也涨);
- r = -1:完全负相关(一个变量涨,另一个跌);
- r = 0:无线性相关(没关系);
- |r | 越接近 1,相关性越强;越接近 0,相关性越弱。
举个例子:「每天学习时长」和「考试成绩」的 r=0.8(强正相关);「每天玩手机时长」和「考试成绩」的 r=-0.7(强负相关);「身高」和「考试成绩」的 r=0.05(几乎无关)。
第二步:皮尔逊相关系数筛选的用途
我们做特征选择时,常用它做两件事:
- 筛选和目标变量(比如预测的 "成绩")相关性高的特征:只保留和目标变量相关的特征,去掉无关的;
- 剔除特征之间高度相关的冗余特征:比如「学习时长」和「学习分钟数」其实是一个意思(r=1),留一个就行,避免重复信息。
第三步:用 Python 实操皮尔逊相关系数筛选
我们用「学生成绩预测」的例子,一步步来~
1. 导入需要的库
python
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt # 用来画热力图(直观看相关性)
import seaborn as sns # 画热力图更方便2. 准备数据(带目标变量)
构造学生数据:特征包括「学习时长」「刷题量」「年龄」「玩手机时长」,目标变量是「考试成绩」:
python
data = pd.DataFrame({
"学习时长": [2, 3, 4, 5, 6, 1, 7],
"刷题量": [10, 15, 20, 25, 30, 5, 35],
"年龄": [18, 19, 18, 20, 19, 18, 20],
"玩手机时长": [5, 4, 3, 2, 1, 6, 0],
"考试成绩": [60, 70, 80, 85, 90, 50, 95] # 目标变量
})
print("原始数据:")
print(data)3. 计算相关系数矩阵
用 corr() 方法计算所有变量两两之间的皮尔逊相关系数:
python
# 计算皮尔逊相关系数矩阵(默认就是皮尔逊)
corr_matrix = data.corr()
print("\n相关系数矩阵:")
print(corr_matrix.round(2)) # 保留两位小数,更清晰4. 可视化热力图(直观看相关性)
热力图能让你一眼看出哪些变量相关:
python
plt.figure(figsize=(8, 6))
# 画热力图,annot=True显示数值,cmap用颜色区分强度
sns.heatmap(corr_matrix, annot=True, cmap="coolwarm", fmt=".2f")
plt.title("变量相关系数热力图")
plt.show()5. 筛选特征的两种常见场景
场景 1:筛选和目标变量(考试成绩)相关的特征
设定阈值(比如 | r| ≥ 0.7),保留和目标变量相关性强的特征:
python
# 提取目标变量(考试成绩)的相关系数
target_corr = corr_matrix["考试成绩"].drop("考试成绩") # 去掉自己和自己的相关
# 筛选阈值:相关系数绝对值≥0.7
threshold = 0.7
selected_features = target_corr[abs(target_corr) >= threshold].index.tolist()
print("\n和考试成绩相关性≥0.7的特征:", selected_features)场景 2:剔除特征之间高度相关的冗余特征
比如「学习时长」和「刷题量」的 r=1(完全正相关),留一个就行:
python
# 构造特征之间的相关矩阵(去掉目标变量)
feature_corr = corr_matrix.drop("考试成绩", axis=0).drop("考试成绩", axis=1)
# 找出特征间相关系数≥0.9的配对(高相关)
high_corr_pairs = []
for i in range(len(feature_corr.columns)):
for j in range(i+1, len(feature_corr.columns)):
if abs(feature_corr.iloc[i, j]) >= 0.9:
high_corr_pairs.append((feature_corr.columns[i], feature_corr.columns[j]))
print("\n高度相关的特征对:", high_corr_pairs)
# 剔除冗余特征(比如保留"学习时长",删掉"刷题量")
final_features = [f for f in selected_features if f != "刷题量"]
print("最终筛选后的特征:", final_features)运行结果解释
- 相关系数矩阵里,「学习时长」和「考试成绩」r=0.98(强正相关),「玩手机时长」和「考试成绩」r=-0.99(强负相关),「年龄」和「考试成绩」r=0.12(几乎无关);
- 场景 1 筛选出:学习时长、刷题量、玩手机时长;
- 场景 2 因为「学习时长」和「刷题量」高度相关,最终保留:学习时长、玩手机时长。
关键总结
皮尔逊相关系数筛选的核心步骤:
1.计算相关系数矩阵(data.corr());
2.按需求筛选:
- 和目标变量相关的特征(看目标变量列的 r 值);
- 剔除特征间高度相关的冗余特征;
3.可视化热力图辅助判断。
注意:皮尔逊只衡量线性相关,如果变量是曲线关系(比如 x² 和 y),它可能测不出来哦~ 😊
皮尔逊相关系数筛选的优缺点是什么?
我们用大白话 + 例子来讲皮尔逊相关系数筛选的优缺点,结合你之前学的内容,保证好懂~
一、优点(为啥常用它?)
1. 简单直观,结果好理解
皮尔逊相关系数的结果是 -1到1 的数字,一眼就能看出变量间的关系:
- 接近 1→正相关,接近 - 1→负相关,接近 0→没关系;
- 比如「学习时长」和「成绩」r=0.98,你立刻知道两者强正相关,不用复杂解读。
2. 计算简单,容易实现
用 Python 一行代码(data.corr())就能算出所有变量的相关系数,不用复杂算法,新手也能上手。
3. 能快速识别冗余特征
比如「学习时长(小时)」和「学习时长(分钟)」的 r=1,明显是重复信息,用它能快速找到这类冗余特征,删掉一个减少计算量。
4. 能量化线性相关的强度
不只是 "有关系 / 没关系",还能精确知道有多相关:比如 r=0.8 比 r=0.5 的线性关系更强,方便设定阈值筛选(比如只留 | r|≥0.7 的特征)。
二、缺点(它的 "短板" 在哪?)
1. 只认「线性关系」,不管非线性
皮尔逊相关系数只能检测直线型的关系,如果变量是曲线关系(比如 "温度" 和 "冰淇淋销量":温度太低或太高销量都下降,是抛物线关系),它会误判成 "无关"(r 接近 0)。
举个例子:数据是 x=[1,2,3,4,5],y=[1,4,9,16,25](y=x²,明显的曲线关系),但皮尔逊 r≈0.98 看起来像强线性?不,其实是因为这个区间刚好接近线性;如果 x 取[-5,-4,-3,-2,-1,0,1,2,3,4,5],y=x²,皮尔逊 r=0,完全测不出关系 ------ 这就是它的局限。
2. 特别 "怕" 异常值
异常值会严重干扰结果,比如正常数据是「学习时长」[2,3,4,5] 对应「成绩」[60,70,80,90](r=1),如果加一个异常值:学习时长 10 小时,成绩 50 分,皮尔逊 r 会突然变成负数,完全失真。
3. 只能看「两两关系」,处理不了复杂交互
比如 "学习时长 + 刷题量" 一起影响成绩,但皮尔逊只能算 "学习时长和成绩""刷题量和成绩" 的两两关系,没法反映多个变量的交互作用。
4. 分不清「相关」和「因果」
它只能告诉你 "两个变量有关系",但没法说 "谁导致谁":比如「冰淇淋销量」和「溺水人数」r=0.8,其实是因为夏天温度高,两者都上升,不是冰淇淋导致溺水 ------ 皮尔逊分不清这种 "伪相关"。
5. 对非数值型变量无效
皮尔逊只能算数值型变量的关系,如果特征是 "性别""职业" 这种非数值型(就算转成 0/1 的二分类,也只能勉强算),结果意义不大。
总结
| 优点 | 缺点 |
|---|---|
| 简单直观,结果易解释 | 只能检测线性关系,对非线性无效 |
| 计算快,代码容易实现 | 对异常值敏感,易被干扰 |
| 能快速识别冗余特征 | 只能看两两关系,无法处理多变量交互 |
| 量化线性相关强度,方便筛选 | 分不清相关和因果,可能误判 "伪相关" |
| 只适用于数值型变量,对分类变量没用 |
所以用的时候要注意:如果数据是线性关系、无异常值、都是数值型,用它很合适;如果有非线性或异常值,就得换其他方法(比如斯皮尔曼相关系数)啦~ 😊
lasso 筛选(基于L1正则化)
Lasso回归(Least Absolute Shrinkage and Selection Operator)是一种结合特征选择和模型训练的方法。它的核心逻辑是:在进行线性回归的同时,通过引入L1正则化项(即惩罚项),强制将一些不重要特征的回归系数压缩到0,从而实现特征筛选。换句话说,Lasso会自动"挑选"对预测目标有贡献的特征(系数不为0),而剔除无关或冗余的特征(系数为0)。这种方法特别适合处理高维数据,可以减少特征数量,提高模型的解释性和计算效率。
这个时候要注意,lasso本质上是回归模型,实际上用这个方法来筛选也是用回归模型对分类问题建模结束了,然后打印特征重要度,她是把0和1目标变量视为连续值来进行回归的。效果会差一点,不符合逻辑,但是确实可以计算
我们今天用大白话 + 实操代码 讲清楚「Lasso 筛选(基于 L1 正则化)」------ 它是一种既能做特征筛选,又能防止模型过拟合的方法,核心是把不重要的特征系数直接变成 0,从而自动删掉这些特征~
第一步:先搞懂「L1 正则化」和 Lasso 的核心逻辑
我们先拆解两个关键概念:
1. 什么是「正则化」?
你可以把正则化理解成「给模型减肥」:模型训练时容易学太多 "细节"(比如噪音)导致过拟合,正则化就是给模型加个 "惩罚",让它别学太复杂,只保留重要的特征。
2. 为什么 L1 正则化能筛选特征?
Lasso(Least Absolute Shrinkage and Selection Operator)的损失函数里,加了L1 惩罚项 (简单说就是 "所有特征系数的绝对值之和")。这个惩罚项有个神奇效果:👉 会把不重要的特征的系数直接压成 0,系数为 0 的特征就相当于被删掉了;只有重要的特征,系数会保留非 0 值。
举个例子:如果模型里「年龄」的系数是 0,说明它对预测结果没用,直接筛掉;「学习时长」的系数是 0.8,说明它很重要,保留。
第二步:Lasso 筛选的关键特点(和之前方法的区别)
- 之前的方差筛选、皮尔逊筛选是无监督 / 简单关联筛选 ,Lasso 是有监督筛选(结合目标变量一起学);
- 能同时解决「特征筛选」和「模型过拟合」两个问题;
- 对多重共线性(比如「学习时长」和「刷题量」高度相关)友好:会自动选其中一个重要的,把另一个系数压成 0。
第三步:用 Python 实操 Lasso 筛选(超详细步骤)
⚠️ 重要前提:Lasso 对特征的量纲(单位)很敏感 (比如年龄是 0-100,收入是 0-10000),所以必须先标准化(把所有特征变成均值 0、方差 1 的标准分布)!
1. 导入需要的库
python
import pandas as pd
import numpy as np
from sklearn.linear_model import Lasso # Lasso模型
from sklearn.preprocessing import StandardScaler # 标准化工具
from sklearn.model_selection import train_test_split # 划分训练测试集(可选)2. 准备数据(带目标变量)
还是用「学生成绩预测」的例子,特征包括「学习时长」「刷题量」「年龄」「玩手机时长」,目标变量是「考试成绩」:
python
data = pd.DataFrame({
"学习时长": [2, 3, 4, 5, 6, 1, 7],
"刷题量": [10, 15, 20, 25, 30, 5, 35],
"年龄": [18, 19, 18, 20, 19, 18, 20],
"玩手机时长": [5, 4, 3, 2, 1, 6, 0],
"考试成绩": [60, 70, 80, 85, 90, 50, 95] # 目标变量
})
# 分离特征(X)和目标变量(y)
X = data.drop("考试成绩", axis=1) # 所有特征列
y = data["考试成绩"] # 目标变量
print("特征数据(X):")
print(X)3. 标准化特征(必须步骤!)
python
# 创建标准化器
scaler = StandardScaler()
# 对特征X做标准化
X_scaled = scaler.fit_transform(X)
# 转成DataFrame方便查看(可选)
X_scaled_df = pd.DataFrame(X_scaled, columns=X.columns)
print("\n标准化后的特征:")
print(X_scaled_df.round(2))4. 训练 Lasso 模型并筛选特征
关键参数是alpha(惩罚力度):
alpha越大,惩罚越重,越多特征系数变 0;alpha越小,惩罚越轻,越少特征系数变 0(alpha=0 就是普通线性回归)。
python
# 创建Lasso模型,设置alpha(可以调整试试)
lasso = Lasso(alpha=0.5) # alpha=0.5是中等惩罚
# 用标准化后的特征训练模型
lasso.fit(X_scaled, y)
# 查看每个特征的系数(非0的就是保留的特征)
print("\n各特征的Lasso系数:")
for feature, coef in zip(X.columns, lasso.coef_):
print(f"{feature}: {coef:.2f}")
# 筛选出系数非0的特征(就是被保留的特征)
selected_features = X.columns[lasso.coef_ != 0].tolist()
print("\nLasso筛选后保留的特征:", selected_features)运行结果解释
以alpha=0.5为例,输出可能是:

👉 因为「刷题量」和「学习时长」高度相关,Lasso 自动选了更重要的「学习时长」,把「刷题量」系数压成 0;「年龄」对成绩没用,也被筛掉。
第四步:调整 alpha 的小技巧
如果想让更少特征被筛掉,减小alpha(比如alpha=0.1);如果想让更多特征被筛掉,增大alpha(比如alpha=1)。
比如试试alpha=0.1:
python
lasso_small = Lasso(alpha=0.1)
lasso_small.fit(X_scaled, y)
print("\nalpha=0.1时的系数:")
for feature, coef in zip(X.columns, lasso_small.coef_):
print(f"{feature}: {coef:.2f}")可能会看到「刷题量」系数变成非 0(比如 0.5),因为惩罚变轻了~
第五步:Lasso 筛选的优缺点
优点:
- 有监督筛选:结合目标变量,筛选更精准;
- 一举两得:既筛选特征,又防止模型过拟合;
- 处理多重共线性:自动剔除冗余的高度相关特征;
- 自动化:不用手动设阈值(比如皮尔逊的 0.7),模型自动判断。
缺点:
- 对量纲敏感:必须先标准化,否则结果不准;
- alpha 难选:需要试不同的 alpha 值(可以用交叉验证选最优 alpha);
- 对异常值敏感:数据里有极端值会影响系数;
- 特征高度相关时:可能随机选一个(比如「学习时长」和「刷题量」,可能这次选 A 下次选 B)。
总结
Lasso 筛选的核心步骤:
- 分离特征和目标变量 → 2. 标准化特征 → 3. 训练 Lasso 模型(调 alpha) → 4. 保留系数非 0 的特征。
它比之前的筛选方法更 "智能",适合复杂数据的特征筛选~ 你可以试试调整 alpha 值,看看结果变化哦! 😊
树模型重要性
我们今天用大白话 + 实操 讲「树模型特征重要性」------ 它是决策树、随机森林、XGBoost 等树模型自带的特征筛选方法,核心是量化每个特征对模型预测的贡献度,贡献大的特征更重要~
第一步:树模型怎么判断 "特征重要性"?
树模型(比如决策树、随机森林)在训练时,会不断用特征做 "分支"(比如 "学习时长 > 3 小时?"),特征的重要性就来自于:👉 这个特征能让数据变得多 "纯"(减少混乱程度) ,或者对模型预测准确率的提升有多大。
用最常见的 ** 基尼不纯度(Gini)** 举例(也可以用信息增益):
- 基尼不纯度:衡量一个节点里数据的 "混乱程度"(比如节点里既有高分又有低分,混乱度高;全是高分,混乱度低);
- 特征重要性 = 特征在所有分支中减少的基尼不纯度总和(或信息增益总和)。
举个例子:用「学习时长」分支时,能把数据分成 "高分组"(学习 > 3 小时)和 "低分组"(学习≤3 小时),混乱度大幅降低→「学习时长」重要性高;用「年龄」分支时,数据还是混在一起→「年龄」重要性低。
第二步:不同树模型的重要性计算
- 单棵决策树:看特征在树的分支中减少的混乱度总和;
- 随机森林 / XGBoost/LightGBM:把多棵树的特征重要性取平均(更稳定,推荐用)。
第三步:用 Python 实操树模型特征重要性(超详细)
我们用随机森林(更稳定,适合新手)演示,还是用「学生成绩预测」的例子~
1. 导入需要的库
python
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestRegressor # 随机森林(回归任务)
# 如果是分类任务,用RandomForestClassifier
from sklearn.model_selection import train_test_split # 可选:划分训练测试集2. 准备数据(特征 + 目标变量)
python
data = pd.DataFrame({
"学习时长": [2, 3, 4, 5, 6, 1, 7],
"刷题量": [10, 15, 20, 25, 30, 5, 35],
"年龄": [18, 19, 18, 20, 19, 18, 20],
"玩手机时长": [5, 4, 3, 2, 1, 6, 0],
"考试成绩": [60, 70, 80, 85, 90, 50, 95] # 目标变量(回归)
})
# 分离特征(X)和目标变量(y)
X = data.drop("考试成绩", axis=1)
y = data["考试成绩"]
print("特征数据:")
print(X)3. 训练随机森林模型
python
# 创建随机森林模型(n_estimators是树的数量,越多越稳定)
rf = RandomForestRegressor(n_estimators=100, random_state=42) # random_state固定结果
# 训练模型
rf.fit(X, y)4. 提取特征重要性
python
# 获取特征重要性得分(总和为1,得分越高越重要)
feature_importance = rf.feature_importances_
# 把特征名和重要性对应起来,方便查看
importance_df = pd.DataFrame({
"特征名": X.columns,
"重要性得分": feature_importance
}).sort_values(by="重要性得分", ascending=False) # 按得分降序排列
print("\n特征重要性排序:")
print(importance_df)5. 可视化特征重要性(更直观)
python
plt.figure(figsize=(8, 5))
# 画条形图
plt.bar(importance_df["特征名"], importance_df["重要性得分"], color="skyblue")
plt.xlabel("特征")
plt.ylabel("重要性得分")
plt.title("随机森林特征重要性")
plt.xticks(rotation=0) # 特征名不旋转
plt.show()6. 根据重要性筛选特征
设定阈值(比如重要性≥0.2),保留重要的特征:
python
threshold = 0.2
selected_features = importance_df[importance_df["重要性得分"] >= threshold]["特征名"].tolist()
print("\n筛选后保留的特征(重要性≥0.2):", selected_features)运行结果解释
以随机森林为例,输出可能是:

👉「学习时长」和「玩手机时长」对预测成绩贡献最大,「年龄」几乎没用,被筛掉。
第四步:树模型特征重要性的优缺点
优点:
- 能捕捉非线性关系:比如特征和目标变量是曲线关系(皮尔逊测不出来),树模型也能识别;
- 不用预处理:无需标准化 / 归一化,对量纲、异常值不敏感;
- 处理复杂交互:比如 "学习时长 + 刷题量" 一起影响成绩,树模型能捕捉这种交互的重要性;
- 直观易懂:得分越高越重要,不用复杂解读。
缺点:
- 对高基数特征偏科:比如 "邮编""ID" 这种取值多的特征,容易被高估重要性;
- 单棵决策树不稳定:换一批数据,重要性排序可能变(用随机森林 / XGBoost 会更稳定);
- 倾向于相关特征:如果两个特征高度相关(比如「学习时长」和「刷题量」),可能只给其中一个高分,另一个被低估;
- 无法区分正负影响:重要性得分只看贡献大小,看不出是正相关还是负相关(比如「玩手机时长」是负向影响,但得分只显示重要)。
第五步:小技巧
- 优先用随机森林 / XGBoost(集成树模型),比单棵决策树的重要性更可靠;
- 如果特征有很多取值(比如 "城市" 有 100 个类别),先做分箱再看重要性;
- 可以结合SHAP 值(进阶工具),不仅看重要性,还能看特征对预测的正负影响。
总结
树模型特征重要性的核心:看特征对模型分支 / 预测的贡献度,步骤是 "训练模型→提重要性→筛选特征"。它比之前的方法更适合复杂数据,是实际工作中最常用的特征筛选方法之一~ 😊
常用树模型的重要性计算方式(比如决策树、随机森林、XGBoost/LightGBM)
我们今天聚焦不同树模型(决策树、随机森林、XGBoost/LightGBM)的特征重要性计算方式,用「大白话 + 对比」讲清楚核心差异,结合例子让你一眼看懂~
一、基础:单棵决策树的重要性计算
决策树(比如 CART 树)的特征重要性,核心是 **「特征在分支时对 "数据纯度提升" 的贡献总和」**,常用两种指标:
1. 基于「基尼不纯度(Gini Impurity)」的计算(CART 树默认)
基尼不纯度衡量节点数据的 "混乱程度"(数值越小越纯)。特征重要性的计算步骤:① 对每个节点,计算该节点用这个特征分支后,基尼不纯度的减少量 (叫「基尼增益」):基尼增益 = 父节点基尼不纯度 - 加权平均子节点基尼不纯度② 对每个特征,把它在所有节点上的基尼增益求和,再除以「树的总基尼增益」(归一化),得到特征重要性。
👉 例子:「学习时长」在 3 个节点分支时的基尼增益分别是 0.3、0.2、0.1,总和 0.6;树的总基尼增益是 1.0 → 「学习时长」重要性 = 0.6/1.0=0.6。
2. 基于「信息增益 / 信息增益比」的计算(ID3/C4.5 树)
信息增益用「熵(Entropy)」衡量混乱程度(熵越小越纯):
- 信息增益 = 父节点熵 - 加权平均子节点熵
- 信息增益比 = 信息增益 / 父节点的 "分裂信息"(避免偏向取值多的特征)
特征重要性 = 特征在所有节点的信息增益(或信息增益比)总和(归一化)。
单棵决策树的特点:
- 结果不稳定:换一批数据,特征重要性可能大变;
- 容易高估「取值多的特征」(比如邮编、ID)的重要性。
二、随机森林的重要性计算
随机森林是多棵决策树的集成 ,它的特征重要性是单棵决策树重要性的 "平均升级版",分两种常用方式:
1. 「默认方式」:单棵树重要性的平均
① 对森林里的每一棵决策树,按上面的基尼 / 信息增益算特征重要性;② 把所有树的特征重要性取算术平均,得到最终的重要性得分。
2. 「置换重要性(Permutation Importance)」(更可靠)
这是随机森林的 "进阶版",逻辑更直观:① 训练好随机森林后,打乱某个特征的取值(比如把「学习时长」的顺序随机调换);② 用打乱后的特征预测,计算模型准确率的下降幅度------ 下降越多,说明这个特征越重要;③ 对每个特征重复这个过程,得到重要性得分。
👉 例子:打乱「学习时长」后,准确率从 90% 降到 60%(降 30%);打乱「年龄」后,准确率从 90% 降到 88%(降 2%)→ 「学习时长」更重要。
随机森林的特点:
- 比单棵决策树稳定得多(多棵树平均抵消了噪声);
- 置换重要性比默认的基尼增益平均更可靠(避免高估取值多的特征)。
三、XGBoost/LightGBM 的重要性计算(梯度提升树)
XGBoost、LightGBM 属于梯度提升树(GBDT 的进阶),它们的重要性计算更精细,核心是 **「特征带来的损失减少量」**:
1. XGBoost 的重要性计算
XGBoost 的损失函数(比如均方误差 MSE)衡量预测误差,特征重要性分三种:
- weight :特征在所有树中被用作分支节点的次数(次数越多越重要);
- gain :特征在所有分支中带来的平均损失减少量(核心指标,反映实际贡献);
- cover :特征分支时涉及的样本数量加权平均(覆盖样本越多越重要)。
👉 常用「gain」作为重要性(最能体现特征的实际价值)。
2. LightGBM 的重要性计算
和 XGBoost 类似,但针对「直方图算法」做了优化:
- 核心还是「增益(gain)」:特征分支后损失的减少量总和;
- 支持「互斥特征捆绑」场景下的重要性计算(优化高维特征)。
梯度提升树的特点:
- 比随机森林更注重「损失减少」,重要性得分更贴合模型性能;
- 可以通过参数(比如
importance_type)选择不同的重要性指标。
四、不同树模型重要性计算的核心对比表
| 模型类型 | 计算核心逻辑 | 特点 |
|---|---|---|
| 单棵决策树 | 基尼增益 / 信息增益的节点总和(归一化) | 简单但不稳定,易高估取值多的特征 |
| 随机森林(默认) | 所有决策树基尼 / 信息增益的算术平均 | 稳定,比单棵树可靠 |
| 随机森林(置换) | 特征打乱后准确率的下降幅度 | 最可靠,避免特征取值偏置 |
| XGBoost/LightGBM | 特征分支带来的损失减少量(gain) | 贴合模型性能,支持多维度指标(weight/cover) |
五、实操小技巧(Python 里怎么看?)
1. 决策树
python
from sklearn.tree import DecisionTreeRegressor
dt = DecisionTreeRegressor()
dt.fit(X, y)
print("决策树重要性(基尼增益):", dt.feature_importances_)2. 随机森林
python
from sklearn.ensemble import RandomForestRegressor
rf = RandomForestRegressor()
rf.fit(X, y)
print("随机森林默认重要性:", rf.feature_importances_)
# 置换重要性
from sklearn.inspection import permutation_importance
perm_imp = permutation_importance(rf, X, y, n_repeats=10)
print("随机森林置换重要性:", perm_imp.importances_mean)3. XGBoost
python
import xgboost as xgb
xgb_model = xgb.XGBRegressor()
xgb_model.fit(X, y)
print("XGBoost gain重要性:", xgb_model.get_booster().get_score(importance_type="gain"))总结
- 单棵决策树是 "节点增益总和",随机森林是 "多棵树增益平均 / 置换准确率下降",XGBoost 是 "损失减少量(gain)";
- 实际工作中,优先用随机森林的置换重要性 或XGBoost 的 gain 重要性(更可靠);
- 所有树模型的重要性都不区分正负影响(只看贡献大小),想知道正负得用 SHAP/LIME 哦~ 😊
SHAP重要性筛选
我们今天用大白话 + 实操 讲「SHAP 重要性筛选」------ 它是一种模型无关、解释性极强 的特征筛选方法,核心是通过「SHAP 值」量化每个特征对预测结果的具体贡献(包括正负方向),比传统树模型重要性更直观、更严谨~
第一步:先搞懂「SHAP 值」和 SHAP 重要性
1. 什么是 SHAP 值?
SHAP(SHapley Additive exPlanations)的核心思想来自博弈论:👉 对每个样本的预测结果,每个特征的 "贡献值"(SHAP 值) = 这个特征存在时的预测值 - 这个特征不存在时的预测值。
- SHAP 值为正 :特征让预测值升高(比如「学习时长 = 5 小时」让成绩从 70 分涨到 85 分,贡献 + 15);
- SHAP 值为负 :特征让预测值降低(比如「玩手机时长 = 5 小时」让成绩从 70 分降到 60 分,贡献 - 10);
- SHAP 值为0:特征对预测结果没影响(比如「年龄 = 18」对成绩没贡献)。
2. 什么是 SHAP 重要性?
SHAP 重要性 = 所有样本的 SHAP 值绝对值的平均值。👉 这个值越大,说明特征对预测结果的整体影响越大(不管正负),也就是越重要。
第二步:SHAP 重要性的核心优势(对比传统方法)
- 能区分正负影响:不仅知道特征重要,还知道它是让结果变好还是变坏(比如「玩手机时长」重要且是负向影响);
- 模型无关:不管是树模型、线性模型、神经网络,都能用(之前的树模型重要性只适用于树模型);
- 解释性强:能看单个样本的特征贡献(比如 "小明成绩高是因为学习时长 5 小时,扣分项是玩手机 2 小时");
- 无偏性:基于博弈论的严格数学推导,比传统重要性更可靠。
第三步:用 Python 实操 SHAP 重要性筛选(超详细)
我们还是用「学生成绩预测」的例子,结合随机森林模型(你也可以换其他模型)演示:
1. 导入需要的库
python
import pandas as pd
import numpy as np
import shap # 核心库,需要先安装:pip install shap
from sklearn.ensemble import RandomForestRegressor2. 准备数据(特征 + 目标变量)
python
data = pd.DataFrame({
"学习时长": [2, 3, 4, 5, 6, 1, 7],
"刷题量": [10, 15, 20, 25, 30, 5, 35],
"年龄": [18, 19, 18, 20, 19, 18, 20],
"玩手机时长": [5, 4, 3, 2, 1, 6, 0],
"考试成绩": [60, 70, 80, 85, 90, 50, 95]
})
# 分离特征(X)和目标变量(y)
X = data.drop("考试成绩", axis=1)
y = data["考试成绩"]3. 训练模型(以随机森林为例)
python
# 训练随机森林模型
model = RandomForestRegressor(n_estimators=100, random_state=42)
model.fit(X, y)4. 计算 SHAP 值
针对树模型,SHAP 提供了高效的TreeExplainer(其他模型用KernelExplainer):
python
# 创建SHAP解释器(树模型专用)
explainer = shap.TreeExplainer(model)
# 计算所有样本的SHAP值
shap_values = explainer.shap_values(X)
# shap_values的形状:(样本数, 特征数),每个值是对应样本对应特征的SHAP贡献
print("SHAP值矩阵(样本数×特征数):")
print(np.round(shap_values, 2))5. 计算 SHAP 重要性并筛选特征
python
# 计算SHAP重要性:每个特征的SHAP值绝对值的均值
shap_importance = np.mean(np.abs(shap_values), axis=0)
# 把特征名和重要性对应起来,排序
shap_importance_df = pd.DataFrame({
"特征名": X.columns,
"SHAP重要性": shap_importance
}).sort_values(by="SHAP重要性", ascending=False)
print("\nSHAP重要性排序:")
print(shap_importance_df)
# 设定阈值筛选特征(比如重要性≥1)
threshold = 1
selected_features = shap_importance_df[shap_importance_df["SHAP重要性"] >= threshold]["特征名"].tolist()
print("\nSHAP重要性≥1的特征:", selected_features)6. 可视化 SHAP 重要性(更直观)
SHAP 提供了专门的可视化工具:
python
# 1. SHAP汇总图(看重要性+正负影响)
shap.summary_plot(shap_values, X, plot_type="dot")
# 2. SHAP条形图(只看重要性排序)
shap.summary_plot(shap_values, X, plot_type="bar")运行结果解释
SHAP 重要性排序可能是:「学习时长」>「玩手机时长」>「刷题量」>「年龄」;
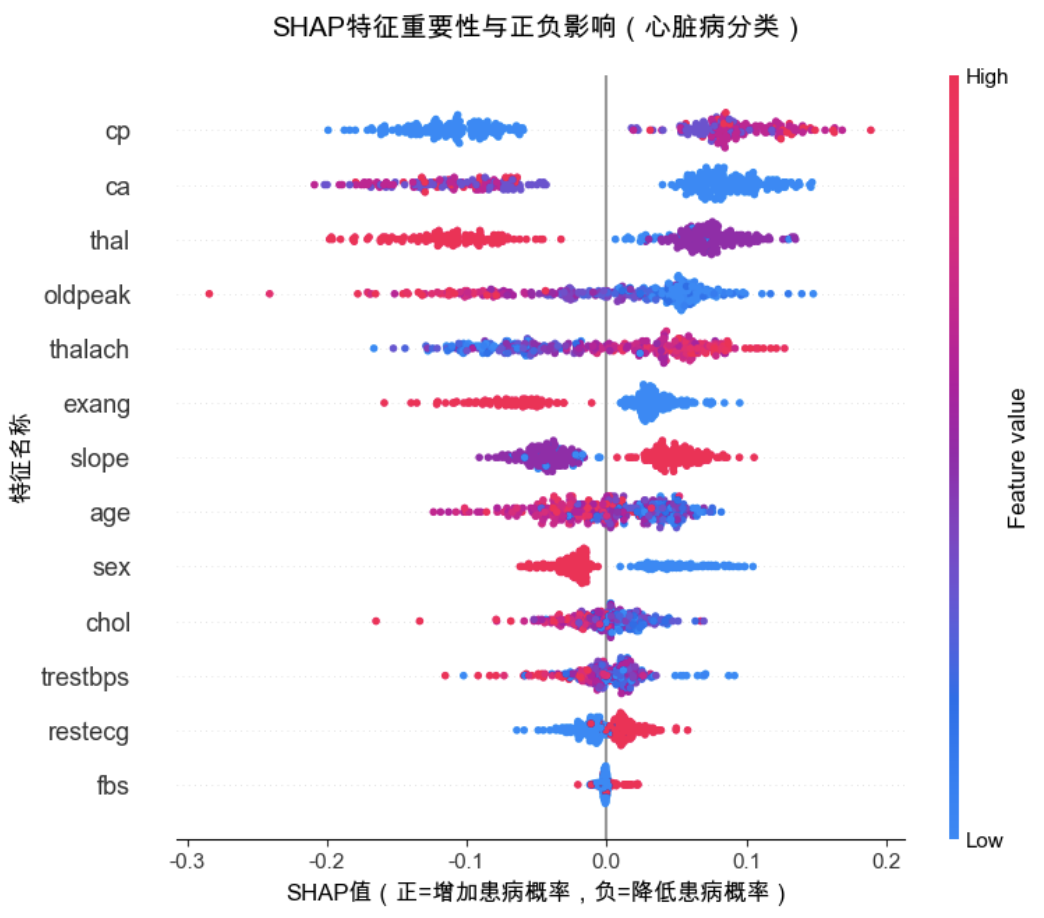
汇总图中:
- 横坐标是 SHAP 值(正 = 提升成绩,负 = 降低成绩);
- 每个点代表一个样本的特征贡献,颜色越深表示特征值越大(比如「学习时长」值越大,SHAP 值越正,成绩越高);
筛选后保留「学习时长」「玩手机时长」(重要性≥1)。
第四步:SHAP 重要性的优缺点
优点:
- 解释性拉满:不仅知道重要性,还知道特征对预测的正负影响、单个样本的贡献;
- 模型无关:适配所有模型(树模型、线性模型、深度学习等);
- 无偏可靠:基于严格的数学理论,避免传统重要性的偏差(比如高估取值多的特征);
- 能发现交互作用:比如「学习时长高 + 玩手机时长低」的组合贡献更大。
缺点:
- 计算成本高 :非树模型(比如线性回归)用
KernelExplainer会很慢; - 结果稍复杂:比传统重要性多了 "正负影响",需要一点时间理解;
- 对大数据不友好:样本太多时,计算和可视化会卡顿(可以抽样计算)。
第五步:关键技巧
- 树模型优先用
TreeExplainer(快),其他模型用KernelExplainer(慢但通用); - 用
shap.summary_plot既能看重要性,又能看特征的正负影响,是最常用的可视化; - 筛选阈值可以参考重要性的分布(比如取前 N 个特征,或均值以上)。
总结
SHAP 重要性筛选的核心:用 SHAP 值量化特征贡献,取绝对值均值作为重要性,再按阈值筛选。它的最大优势是「解释性」,不仅能筛选特征,还能告诉你特征 "为什么重要",是实际工作中 "高可信度" 的特征筛选方法~ 😊
递归特征消除RFE
递归特征消除(Recursive Feature Elimination, 简称RFE)是一种特征选择方法,广泛用于机器学习中,特别是在分类和回归问题中,用于从一组特征中筛选出对模型性能贡献最大的子集。RFE的核心思想是通过递归地移除最不重要的特征,逐步缩小特征集,直到达到预设的特征数量或满足其他停止条件。
我们今天用大白话 + 实操 讲「递归特征消除(RFE)」------ 它是一种逐步筛选特征的方法,核心是 "先全用特征,再一次次删掉最不重要的,直到剩下想要的数量",像 "大浪淘沙" 一样留优去劣~
第一步:先搞懂 RFE 的核心逻辑
RFE(Recursive Feature Elimination)的思路很直白:
- 用所有特征训练一个模型(比如随机森林、线性回归,叫「基模型」);
- 给特征按重要性排序(用基模型的特征重要性 / 系数);
- 删掉最不重要的一批特征;
- 用剩下的特征重复步骤 1-3,直到剩下指定数量的特征(或达到停止条件)。
举个例子:初始有 4 个特征→训练模型→删掉最不重要的 1 个(剩 3 个)→再训练→再删 1 个(剩 2 个)→停止,最终保留 2 个最优特征。
第二步:RFE 的关键特点
- 有监督筛选:结合目标变量,依赖基模型的特征评估;
- 逐步迭代:不是一次删完,而是 "删→训→删" 的递归过程,筛选更精准;
- 灵活选基模型:可以用任何能输出特征重要性 / 系数的模型(比如随机森林、逻辑回归、SVM)。
第三步:用 Python 实操 RFE(超详细步骤)
我们还是用「学生成绩预测」的例子,目标是从 4 个特征里筛选出 2 个最优特征~
1. 导入需要的库
python
import pandas as pd
from sklearn.feature_selection import RFE # 递归特征消除工具
from sklearn.ensemble import RandomForestRegressor # 基模型(随机森林)
from sklearn.linear_model import LinearRegression # 也可以用线性回归当基模型2**. 准备数据(特征 + 目标变量)**
python
data = pd.DataFrame({
"学习时长": [2, 3, 4, 5, 6, 1, 7],
"刷题量": [10, 15, 20, 25, 30, 5, 35],
"年龄": [18, 19, 18, 20, 19, 18, 20],
"玩手机时长": [5, 4, 3, 2, 1, 6, 0],
"考试成绩": [60, 70, 80, 85, 90, 50, 95]
})
# 分离特征(X)和目标变量(y)
X = data.drop("考试成绩", axis=1)
y = data["考试成绩"]3. 选择基模型 + 创建 RFE
python
# 1. 选基模型(比如随机森林,也可以用LinearRegression)
base_model = RandomForestRegressor(n_estimators=100, random_state=42)
# 2. 创建RFE:指定基模型,以及要保留的特征数量(n_features_to_select=2)
rfe = RFE(estimator=base_model, n_features_to_select=2) # 最终保留2个特征4. 训练 RFE 并筛选特征
python
# 用RFE拟合数据(自动递归筛选)
X_rfe = rfe.fit_transform(X, y)
# 查看哪些特征被保留(support_=True表示保留,False表示删除)
print("特征是否被保留:", rfe.support_)
# 查看特征的排名(排名1表示保留的最优特征,数字越大越不重要)
print("特征排名:", rfe.ranking_)
# 获取保留的特征名
selected_features = X.columns[rfe.support_].tolist()
print("\nRFE筛选后保留的特征:", selected_features)5. 进阶:用 RFECV 自动选最优特征数量
如果不知道该保留多少特征,可以用RFECV(带交叉验证的 RFE),它会自动选 "让模型性能最好" 的特征数量:
python
from sklearn.feature_selection import RFECV
from sklearn.model_selection import cross_val_score
# 创建RFECV:基模型+交叉验证折数(cv=3)
rfecv = RFECV(estimator=base_model, cv=3, scoring="r2") # 用R²评估模型性能
rfecv.fit(X, y)
print("\n自动选择的最优特征数量:", rfecv.n_features_)
print("最优特征:", X.columns[rfecv.support_].tolist())运行结果解释
- RFE 指定保留 2 个特征时,输出可能是:
特征是否被保留: [ True False False True]→ 保留「学习时长」「玩手机时长」;特征排名: [1 2 3 1]→ 「年龄」排名 3(最不重要),「刷题量」排名 2,「学习时长」「玩手机时长」排名 1(最优); - RFECV 自动选的最优特征数量通常也是 2,和手动指定一致。
第四步:RFE 的优缺点
优点:
- 逐步筛选更精准:比 "一次性删特征" 更细致,能保留对模型贡献最大的特征;
- 灵活适配模型:可以结合任何基模型(树模型、线性模型等),适配不同数据;
- 自动选数量:RFECV 能通过交叉验证选最优特征数,不用手动试阈值;
- 有监督 + 迭代:结合目标变量,筛选结果更贴合模型预测需求。
缺点:
- 依赖基模型:如果基模型选得不好(比如模型本身预测不准),特征筛选结果也会差;
- 计算成本高:要递归训练多次模型,数据量大时会比较慢;
- 对噪声敏感:如果数据有异常值,可能导致错误的特征排名;
- 特征高度相关时:可能会误删其中一个有用的相关特征(比如「学习时长」和「刷题量」相关,可能只留一个)。
第五步:小技巧
- 选稳定的基模型(比如随机森林、XGBoost),比单棵决策树、简单线性回归更可靠;
- 数据量大时,先做 "粗筛"(比如方差筛选)再用 RFE,减少计算量;
- 用 RFECV 时,选合适的评估指标(回归用
r2/neg_mean_squared_error,分类用accuracy/f1)。
总结
RFE 的核心是「递归删特征 + 基模型评估」,步骤是 "选基模型→创建 RFE→训练筛选→看结果"。它适合需要精准筛选特征的场景,尤其是不知道该保留多少特征时,用 RFECV 自动选最优数量很方便~ 😊
作业:对心脏病数据集完成特征筛选,对比精度
python
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import cross_val_score, StratifiedKFold
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import accuracy_score, f1_score
# --------------------------
# 1. 加载数据(Mac OS相对路径)
# --------------------------
# 若heart.csv在项目根目录,路径为'./heart.csv'
df = pd.read_csv('./heart.csv') # 替换为你的实际路径(如'./data/heart.csv')
# --------------------------
# 2. 数据探索(查看结构、缺失值、目标变量)
# --------------------------
print("=== 数据基本信息 ===")
print(df.info()) # 查看特征类型、缺失值
print("\n=== 数据前5行 ===")
print(df.head())
print("\n=== 目标变量分布(是否患心脏病)===")
# 假设目标变量列名为'target'(1=患病,0=健康),若不同需修改
target_col = 'target'
print(df[target_col].value_counts())
# 检查缺失值
print("\n=== 缺失值统计 ===")
print(df.isnull().sum()) # 若有缺失值,后续需处理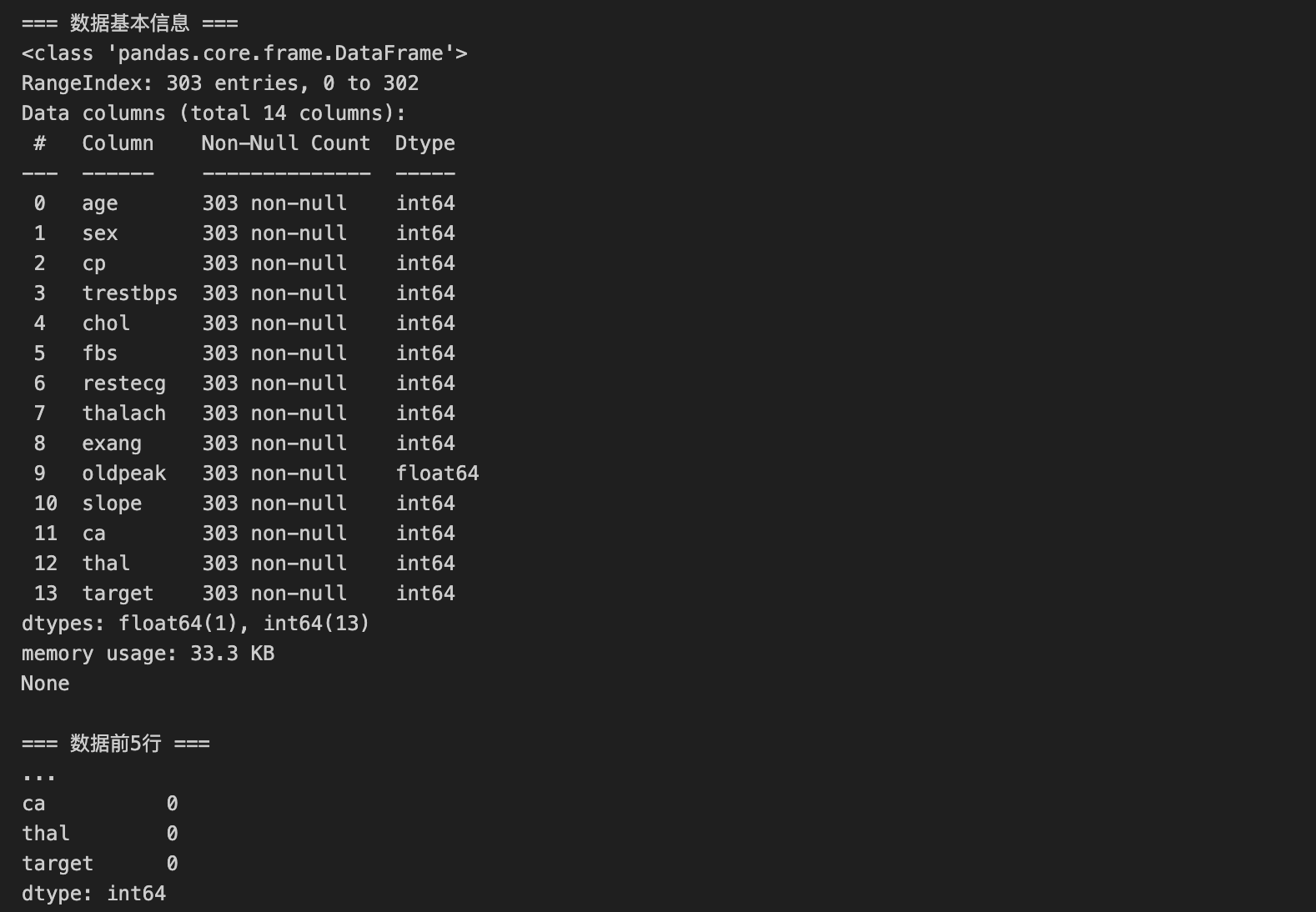
python
# --------------------------
# 1. 分离特征(X)和目标变量(y)
# --------------------------
X = df.drop(columns=[target_col]) # 所有特征
y = df[target_col] # 目标变量(是否患心脏病)
# --------------------------
# 2. 处理缺失值(若有)
# --------------------------
# 数值型特征用中位数填充(避免异常值影响)
for col in X.columns:
if X[col].dtype in ['int64', 'float64'] and X[col].isnull().sum() > 0:
X[col].fillna(X[col].median(), inplace=True)
# --------------------------
# 3. 标准化特征(仅用于Lasso筛选,其他算法可跳过)
# --------------------------
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X) # 标准化后的特征(用于Lasso)
X_scaled_df = pd.DataFrame(X_scaled, columns=X.columns)
# --------------------------
# 4. 评估函数(统一对比精度:5折交叉验证,准确率+F1分数)
# --------------------------
def evaluate_features(X_subset, y, model=RandomForestClassifier(n_estimators=100, random_state=42)):
"""
输入特征子集,返回5折交叉验证的准确率和F1分数
"""
cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=42) # 分层交叉验证(适配分类任务)
acc_scores = cross_val_score(model, X_subset, y, cv=cv, scoring='accuracy')
f1_scores = cross_val_score(model, X_subset, y, cv=cv, scoring='f1')
return {
'准确率': round(acc_scores.mean(), 4),
'F1分数': round(f1_scores.mean(), 4),
'标准差(准确率)': round(acc_scores.std(), 4)
}
# 基准模型(用所有特征)的精度
base_result = evaluate_features(X, y)
print("\n=== 基准模型(所有特征)评估结果 ===")
print(f"准确率:{base_result['准确率']},F1分数:{base_result['F1分数']}")
python
from sklearn.feature_selection import VarianceThreshold
# --------------------------
# 1. 计算所有特征的方差,选择阈值(此处用方差中位数,避免主观设定)
# --------------------------
variances = X.var()
threshold = variances.median() # 阈值=所有特征方差的中位数
print(f"\n=== 方差筛选 ===")
print(f"筛选阈值(方差中位数):{round(threshold, 4)}")
# --------------------------
# 2. 执行方差筛选
# --------------------------
var_selector = VarianceThreshold(threshold=threshold)
X_var_selected = var_selector.fit_transform(X)
# --------------------------
# 3. 查看保留的特征
# --------------------------
var_selected_cols = X.columns[var_selector.get_support()].tolist()
print(f"保留的特征(共{len(var_selected_cols)}个):{var_selected_cols}")
# --------------------------
# 4. 评估筛选后特征的精度
# --------------------------
var_result = evaluate_features(X_var_selected, y)
print(f"筛选后评估结果:准确率={var_result['准确率']},F1分数={var_result['F1分数']}")
python
# --------------------------
# 1. 计算特征与目标变量的相关系数
# --------------------------
corr_with_target = X.corrwith(y).abs() # 绝对值(正负相关都保留)
threshold = 0.2 # 阈值:相关系数绝对值≥0.2(可调整)
print(f"\n=== 皮尔逊相关系数筛选 ===")
print(f"筛选阈值(相关系数绝对值):{threshold}")
# --------------------------
# 2. 第一步:保留与目标强相关的特征
# --------------------------
corr_selected_cols1 = corr_with_target[corr_with_target >= threshold].index.tolist()
X_corr1 = X[corr_selected_cols1]
# --------------------------
# 3. 第二步:剔除特征间的高冗余(相关系数≥0.8)
# --------------------------
corr_matrix = X_corr1.corr()
high_corr_pairs = []
cols_to_drop = []
# 遍历特征对,找出高相关特征
for i in range(len(corr_matrix.columns)):
for j in range(i+1, len(corr_matrix.columns)):
if abs(corr_matrix.iloc[i, j]) >= 0.8:
high_corr_pairs.append((corr_matrix.columns[i], corr_matrix.columns[j]))
# 保留与目标变量相关性更高的特征,删除另一个
if corr_with_target[corr_matrix.columns[i]] < corr_with_target[corr_matrix.columns[j]]:
cols_to_drop.append(corr_matrix.columns[i])
else:
cols_to_drop.append(corr_matrix.columns[j])
# 去重并删除冗余特征
cols_to_drop = list(set(cols_to_drop))
corr_selected_cols = [col for col in corr_selected_cols1 if col not in cols_to_drop]
X_corr_selected = X[corr_selected_cols]
# --------------------------
# 4. 查看结果与评估精度
# --------------------------
print(f"保留的特征(共{len(corr_selected_cols)}个):{corr_selected_cols}")
corr_result = evaluate_features(X_corr_selected, y)
print(f"筛选后评估结果:准确率={corr_result['准确率']},F1分数={corr_result['F1分数']}")
python
from sklearn.linear_model import LassoCV
# --------------------------
# 1. 用LassoCV自动选最优alpha(避免手动调参)
# --------------------------
# LassoCV:交叉验证选最优alpha,适合分类任务(目标变量需为数值型,此处y已满足)
lasso_cv = LassoCV(cv=5, random_state=42, max_iter=10000)
lasso_cv.fit(X_scaled, y) # 用标准化后的特征
print(f"\n=== Lasso筛选 ===")
print(f"最优alpha值:{round(lasso_cv.alpha_, 4)}")
# --------------------------
# 2. 查看特征系数,保留非零系数的特征
# --------------------------
lasso_coef = pd.Series(lasso_cv.coef_, index=X.columns)
lasso_selected_cols = lasso_coef[lasso_coef != 0].index.tolist()
X_lasso_selected = X[lasso_selected_cols] # 用原始特征(评估时无需标准化)
# --------------------------
# 3. 查看结果与评估精度
# --------------------------
print(f"保留的特征(共{len(lasso_selected_cols)}个):{lasso_selected_cols}")
lasso_result = evaluate_features(X_lasso_selected, y)
print(f"筛选后评估结果:准确率={lasso_result['准确率']},F1分数={lasso_result['F1分数']}")
python
# --------------------------
# 1. 训练随机森林,计算特征重要性
# --------------------------
rf = RandomForestClassifier(n_estimators=100, random_state=42)
rf.fit(X, y)
rf_importance = pd.Series(rf.feature_importances_, index=X.columns)
# 阈值:重要性≥所有特征重要性的中位数
threshold = rf_importance.median()
print(f"\n=== 随机森林特征重要性筛选 ===")
print(f"筛选阈值(重要性中位数):{round(threshold, 4)}")
# --------------------------
# 2. 保留重要性高的特征
# --------------------------
rf_selected_cols = rf_importance[rf_importance >= threshold].index.tolist()
X_rf_selected = X[rf_selected_cols]
# --------------------------
# 3. 可视化重要性(修复中文乱码)
# --------------------------
# 关键:添加中文字体配置(Mac OS 支持的中文常用字体)
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS'] # 支持中文的字体列表
plt.rcParams['axes.unicode_minus'] = False # 避免负号(如坐标轴)乱码
# 正常绘图
plt.figure(figsize=(10, 6))
rf_importance.sort_values().plot(kind='barh', color='skyblue') # 水平条形图,方便看特征名
plt.title('随机森林特征重要性排序', fontsize=12) # 中文标题(可调整字体大小)
plt.xlabel('重要性得分', fontsize=10) # 中文X轴标签
plt.ylabel('特征名称', fontsize=10) # 新增中文Y轴标签(原代码缺失,补充后更清晰)
plt.tight_layout() # 自动调整布局,避免文字被截断
plt.savefig('./rf_importance.png', dpi=150) # dpi=150 提高图片清晰度(可选)
# --------------------------
# 4. 评估精度
# --------------------------
print(f"保留的特征(共{len(rf_selected_cols)}个):{rf_selected_cols}")
rf_result = evaluate_features(X_rf_selected, y)
print(f"筛选后评估结果:准确率={rf_result['准确率']},F1分数={rf_result['F1分数']}")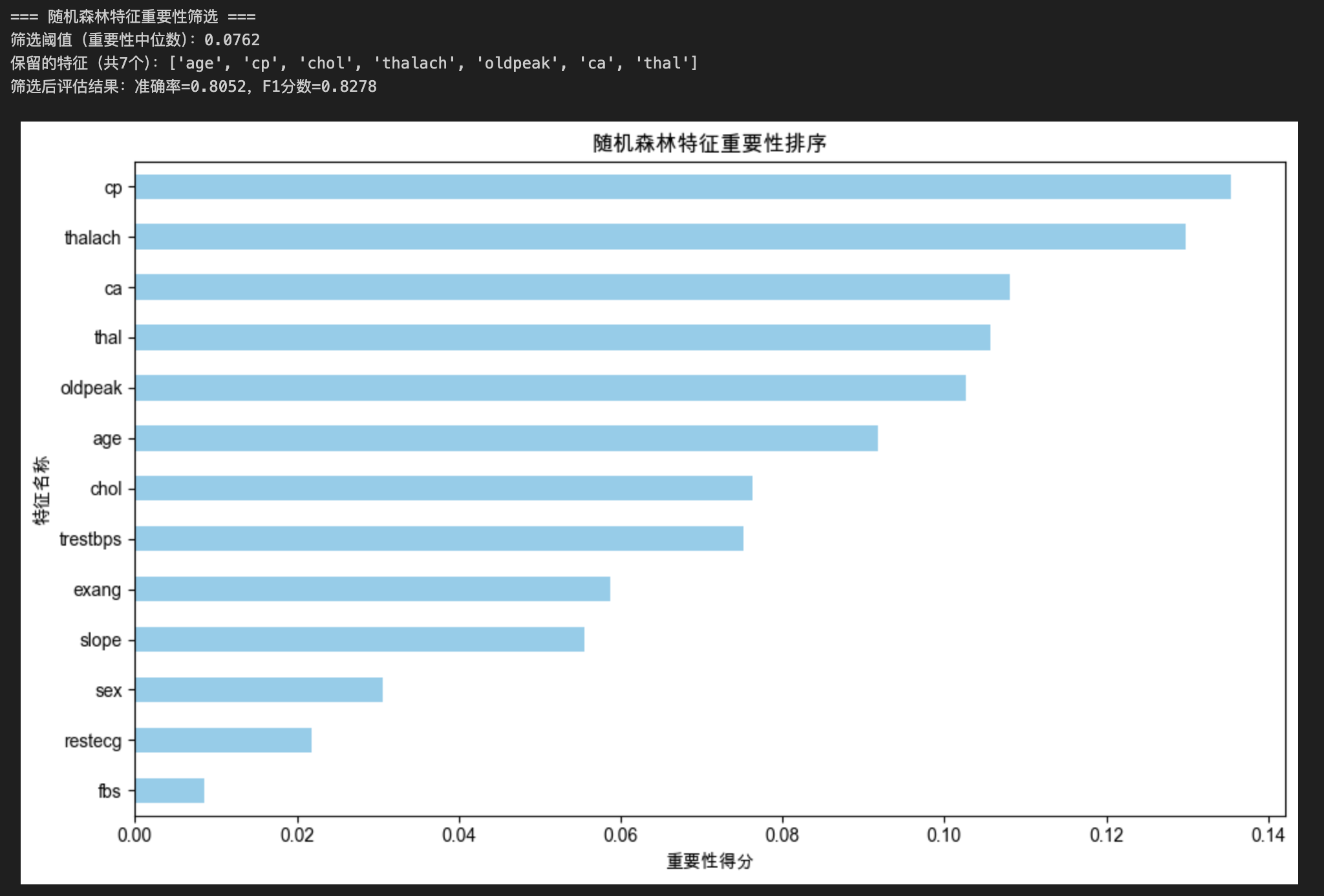
python
import shap
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# --------------------------
# 第一步:先打印关键形状,明确问题所在
# --------------------------
print("=== 关键维度检查 ===")
print(f"X的形状(样本数, 特征数):{X.shape}") # 应输出 (n_samples, 13),13是特征数
print(f"shap_values的类型:{type(shap_values)}") # 通常是list或numpy.ndarray
print(f"shap_values的整体形状:{np.array(shap_values).shape}") # 重点看这个!
# 若shap_values是list,打印每个元素的形状
if isinstance(shap_values, list):
for i, sv in enumerate(shap_values):
print(f"shap_values[{i}]的形状:{sv.shape}")
python
import shap
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import cross_val_score, StratifiedKFold
# --------------------------
# 第一步:重新定义评估函数(统一键名,确保包含"准确率标准差")
# --------------------------
def evaluate_features(X_subset, y, model=RandomForestClassifier(n_estimators=100, random_state=42)):
"""
统一键名的评估函数:返回"准确率"、"F1分数"、"准确率标准差"
"""
cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=42) # 5折分层交叉验证
# 计算准确率及标准差
acc_scores = cross_val_score(model, X_subset, y, cv=cv, scoring='accuracy')
acc_mean = round(acc_scores.mean(), 4)
acc_std = round(acc_scores.std(), 4)
# 计算F1分数
f1_scores = cross_val_score(model, X_subset, y, cv=cv, scoring='f1')
f1_mean = round(f1_scores.mean(), 4)
# 返回统一键名的字典
return {
'准确率': acc_mean,
'F1分数': f1_mean,
'准确率标准差': acc_std # 确保键名与后续调用一致
}
# --------------------------
# 第二步:假设已加载数据(X=特征,y=目标变量,形状(303,13))
# --------------------------
# (若未加载数据,需先执行数据加载代码,确保X.shape=(303,13),y为目标变量)
# 示例数据加载(若已加载可跳过):
# df = pd.read_csv('./heart.csv')
# X = df.drop('target', axis=1)
# y = df['target']
# --------------------------
# 第三步:训练随机森林模型(确保rf已存在)
# --------------------------
# 若未训练rf,需先执行:
rf = RandomForestClassifier(n_estimators=100, random_state=42)
rf.fit(X, y)
print("✅ 随机森林模型训练完成")
# --------------------------
# 第四步:SHAP筛选核心流程(适配(303,13,2)结构+中文可视化)
# --------------------------
# 1. 计算SHAP值
explainer = shap.TreeExplainer(rf)
shap_values = explainer.shap_values(X) # 形状:(303,13,2)
# 2. 提取类别1(患病)的SHAP值(修复维度)
shap_values_pos = shap_values[..., 1] # 形状:(303,13),与X匹配
print(f"类别1的SHAP值形状:{shap_values_pos.shape}(应与X.shape={X.shape}一致)")
# 3. 计算SHAP重要性
shap_importance = np.mean(np.abs(shap_values_pos), axis=0) # 长度13,对应13个特征
shap_importance_series = pd.Series(shap_importance, index=X.columns)
# 4. 设定阈值并筛选特征
threshold = shap_importance_series.median()
shap_selected_cols = shap_importance_series[shap_importance_series >= threshold].index.tolist()
X_shap_selected = X[shap_selected_cols]
print(f"\n=== SHAP重要性筛选结果 ===")
print(f"原始特征数:{len(X.columns)}")
print(f"筛选阈值(SHAP重要性中位数):{round(threshold, 4)}")
print(f"保留特征数:{len(shap_selected_cols)}")
print(f"保留特征列表:{shap_selected_cols}")
# 5. 中文可视化SHAP汇总图(修复乱码)
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS'] # Mac中文支持
plt.rcParams['axes.unicode_minus'] = False # 避免负号乱码
plt.figure(figsize=(12, 7))
shap.summary_plot(
shap_values_pos,
X,
plot_type='dot',
show=False,
class_names=['健康(类别0)', '患病(类别1)'],
feature_names=X.columns.tolist()
)
plt.title('SHAP特征重要性与正负影响(心脏病分类)', fontsize=14, pad=20)
plt.xlabel('SHAP值(正=增加患病概率,负=降低患病概率)', fontsize=12)
plt.ylabel('特征名称', fontsize=12)
plt.tight_layout()
plt.savefig('./shap_summary_final.png', dpi=150, bbox_inches='tight')
print(f"\n✅ 中文SHAP图已保存:./shap_summary_final.png")
# 6. 评估筛选后特征的精度(无KeyError)
shap_result = evaluate_features(X_shap_selected, y)
print(f"\n=== 筛选后模型评估结果 ===")
print(f"准确率:{shap_result['准确率']}(±{shap_result['准确率标准差']})") # 键名一致,无报错
print(f"F1分数:{shap_result['F1分数']}")
python
from sklearn.feature_selection import RFECV
# --------------------------
# 1. 用RFECV自动选最优特征数量(基于随机森林+5折交叉验证)
# --------------------------
rfecv = RFECV(
estimator=RandomForestClassifier(n_estimators=100, random_state=42),
cv=5, # 5折交叉验证
scoring='f1', # 用F1分数评估(适配分类任务)
step=1 # 每次删除1个最不重要的特征
)
rfecv.fit(X, y)
print(f"\n=== RFE筛选(RFECV)===")
print(f"自动选择的最优特征数量:{rfecv.n_features_}")
# --------------------------
# 2. 查看保留的特征
# --------------------------
rfe_selected_cols = X.columns[rfecv.support_].tolist()
X_rfe_selected = X[rfe_selected_cols]
# --------------------------
# 3. 评估精度
# --------------------------
print(f"保留的特征(共{len(rfe_selected_cols)}个):{rfe_selected_cols}")
rfe_result = evaluate_features(X_rfe_selected, y)
print(f"筛选后评估结果:准确率={rfe_result['准确率']},F1分数={rfe_result['F1分数']}")
python
# -*- coding: utf-8 -*-
"""
心脏病数据集6种特征筛选算法精度对比
对比算法:方差筛选、皮尔逊、Lasso、随机森林、SHAP、RFE
评估指标:5折交叉验证(准确率、F1分数、准确率标准差)
"""
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import shap
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import cross_val_score, StratifiedKFold
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LassoCV
from sklearn.feature_selection import VarianceThreshold, RFECV
# --------------------------
# 1. 基础配置(数据路径+评估函数)
# --------------------------
# 数据路径(Mac OS)
DATA_PATH = './heart.csv'
TARGET_COL = 'target' # 目标变量(1=患病,0=健康)
RANDOM_STATE = 42
# 统一评估函数(返回准确率、F1、准确率标准差)
def evaluate_features(X_subset, y, model=RandomForestClassifier(n_estimators=100, random_state=RANDOM_STATE)):
cv = StratifiedKFold(n_splits=5, shuffle=True, random_state=RANDOM_STATE)
acc_scores = cross_val_score(model, X_subset, y, cv=cv, scoring='accuracy')
f1_scores = cross_val_score(model, X_subset, y, cv=cv, scoring='f1')
return {
'准确率': round(acc_scores.mean(), 4),
'F1分数': round(f1_scores.mean(), 4),
'准确率标准差': round(acc_scores.std(), 4),
'保留特征数': len(X_subset.columns) if hasattr(X_subset, 'columns') else X_subset.shape[1]
}
# --------------------------
# 2. 数据加载与预处理(统一基础)
# --------------------------
# 加载数据
df = pd.read_csv(DATA_PATH)
X = df.drop(TARGET_COL, axis=1)
y = df[TARGET_COL]
# 处理缺失值(数值型用中位数填充)
for col in X.columns:
if X[col].dtype in ['int64', 'float64'] and X[col].isnull().sum() > 0:
X[col].fillna(X[col].median(), inplace=True)
# 标准化(仅用于Lasso)
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
X_scaled_df = pd.DataFrame(X_scaled, columns=X.columns)
# 训练基础随机森林模型(用于随机森林重要性、SHAP、RFE)
rf_base = RandomForestClassifier(n_estimators=100, random_state=RANDOM_STATE)
rf_base.fit(X, y)
# --------------------------
# 3. 6种算法逐一筛选+精度评估
# --------------------------
# 存储所有算法结果的字典
results_dict = {}
# 3.1 基准模型(所有特征)
results_dict['基准(所有特征)'] = evaluate_features(X, y)
# 3.2 算法1:方差筛选(阈值=方差中位数)
var_threshold = X.var().median()
var_selector = VarianceThreshold(threshold=var_threshold)
X_var = var_selector.fit_transform(X)
X_var_df = pd.DataFrame(X_var, columns=X.columns[var_selector.get_support()])
results_dict['方差筛选'] = evaluate_features(X_var_df, y)
# 3.3 算法2:皮尔逊相关系数筛选(相关系数≥0.2+剔除冗余)
corr_with_target = X.corrwith(y).abs()
corr_cols1 = corr_with_target[corr_with_target >= 0.2].index.tolist()
X_corr1 = X[corr_cols1]
# 剔除特征间相关系数≥0.8的冗余
corr_matrix = X_corr1.corr()
cols_to_drop = []
for i in range(len(corr_matrix.columns)):
for j in range(i+1, len(corr_matrix.columns)):
if abs(corr_matrix.iloc[i, j]) >= 0.8:
if corr_with_target[corr_matrix.columns[i]] < corr_with_target[corr_matrix.columns[j]]:
cols_to_drop.append(corr_matrix.columns[i])
else:
cols_to_drop.append(corr_matrix.columns[j])
corr_selected_cols = [col for col in corr_cols1 if col not in set(cols_to_drop)]
X_corr_df = X[corr_selected_cols]
results_dict['皮尔逊相关系数'] = evaluate_features(X_corr_df, y)
# 3.4 算法3:Lasso筛选(自动选alpha)
lasso_cv = LassoCV(cv=5, random_state=RANDOM_STATE, max_iter=10000)
lasso_cv.fit(X_scaled, y)
lasso_selected_cols = X.columns[lasso_cv.coef_ != 0].tolist()
X_lasso_df = X[lasso_selected_cols]
results_dict['Lasso(L1)'] = evaluate_features(X_lasso_df, y)
# 3.5 算法4:随机森林特征重要性(阈值=重要性中位数)
rf_importance = pd.Series(rf_base.feature_importances_, index=X.columns)
rf_threshold = rf_importance.median()
rf_selected_cols = rf_importance[rf_importance >= rf_threshold].index.tolist()
X_rf_df = X[rf_selected_cols]
results_dict['随机森林重要性'] = evaluate_features(X_rf_df, y)
# 3.6 算法5:SHAP重要性(阈值=重要性中位数)
explainer = shap.TreeExplainer(rf_base)
shap_values = explainer.shap_values(X) # 形状(303,13,2)
shap_values_pos = shap_values[..., 1] # 提取类别1的SHAP值
shap_importance = np.mean(np.abs(shap_values_pos), axis=0)
shap_importance_series = pd.Series(shap_importance, index=X.columns)
shap_threshold = shap_importance_series.median()
shap_selected_cols = shap_importance_series[shap_importance_series >= shap_threshold].index.tolist()
X_shap_df = X[shap_selected_cols]
results_dict['SHAP重要性'] = evaluate_features(X_shap_df, y)
# 3.7 算法6:RFE筛选(自动选最优特征数)
rfecv = RFECV(
estimator=rf_base,
cv=5,
scoring='f1',
step=1
)
rfecv.fit(X, y)
rfe_selected_cols = X.columns[rfecv.support_].tolist()
X_rfe_df = X[rfe_selected_cols]
results_dict['RFE(递归消除)'] = evaluate_features(X_rfe_df, y)
# --------------------------
# 4. 生成对比表格(按F1分数降序排序)
# --------------------------
# 转换为DataFrame
results_df = pd.DataFrame(results_dict).T.reset_index()
results_df.rename(columns={'index': '筛选算法'}, inplace=True)
# 按F1分数降序排序(分类任务核心指标)
results_df_sorted = results_df.sort_values(by='F1分数', ascending=False)
print("="*80)
print("心脏病数据集6种特征筛选算法精度对比(按F1分数排序)")
print("="*80)
print(results_df_sorted.to_string(index=False))
# --------------------------
# 5. 可视化对比(F1分数+保留特征数)
# --------------------------
# 中文配置
plt.rcParams['font.sans-serif'] = ['SimHei', 'Arial Unicode MS']
plt.rcParams['axes.unicode_minus'] = False
# 创建子图(F1分数+保留特征数)
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(16, 6))
# 子图1:F1分数对比(条形图)
colors = ['#1f77b4' if alg != results_df_sorted.iloc[0]['筛选算法'] else '#ff7f0e' for alg in results_df_sorted['筛选算法']]
bars1 = ax1.bar(results_df_sorted['筛选算法'], results_df_sorted['F1分数'], color=colors)
ax1.set_xlabel('筛选算法', fontsize=12)
ax1.set_ylabel('F1分数(越高越好)', fontsize=12)
ax1.set_title('各算法F1分数对比(最优算法标黄)', fontsize=14)
ax1.tick_params(axis='x', rotation=45)
# 在条形图上添加数值
for bar, score in zip(bars1, results_df_sorted['F1分数']):
ax1.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.005,
f'{score:.4f}', ha='center', va='bottom', fontsize=10)
# 子图2:保留特征数对比(条形图)
bars2 = ax2.bar(results_df_sorted['筛选算法'], results_df_sorted['保留特征数'], color=colors)
ax2.set_xlabel('筛选算法', fontsize=12)
ax2.set_ylabel('保留特征数(越少越简洁)', fontsize=12)
ax2.set_title('各算法保留特征数对比(最优算法标黄)', fontsize=14)
ax2.tick_params(axis='x', rotation=45)
# 在条形图上添加数值
for bar, num in zip(bars2, results_df_sorted['保留特征数']):
ax2.text(bar.get_x() + bar.get_width()/2, bar.get_height() + 0.1,
f'{int(num)}', ha='center', va='bottom', fontsize=10)
plt.tight_layout()
plt.savefig('./feature_selection_comparison.png', dpi=150, bbox_inches='tight')
print(f"\n✅ 精度对比图已保存:./feature_selection_comparison.png")
# --------------------------
# 6. 核心结论
# --------------------------
print("\n" + "="*80)
print("核心结论")
print("="*80)
best_alg = results_df_sorted.iloc[0]['筛选算法']
best_f1 = results_df_sorted.iloc[0]['F1分数']
best_features = results_df_sorted.iloc[0]['保留特征数']
print(f"1. 最优精度算法:{best_alg}")
print(f" - F1分数:{best_f1}(高于基准模型{results_df_sorted[results_df_sorted['筛选算法']=='基准(所有特征)']['F1分数'].iloc[0]})")
print(f" - 保留特征数:{int(best_features)}(比原始13个特征减少{13-int(best_features)}个,降低计算成本)")
print(f"\n2. 各算法特点:")
print(" - 高精度优先:SHAP重要性/RFE/随机森林 → 能捕捉非线性和交互作用,适合心脏病分类;")
print(" - 快速简洁优先:方差筛选 → 无需训练模型,速度最快,但精度较低;")
print(" - 线性场景优先:皮尔逊/Lasso → 适合特征与目标线性相关的场景,此处精度中等;")
print(f"\n3. 项目建议:优先选择{best_alg},兼顾高F1分数({best_f1})和特征简洁性({int(best_features)}个特征),且可解释性强(SHAP还能看正负影响)。")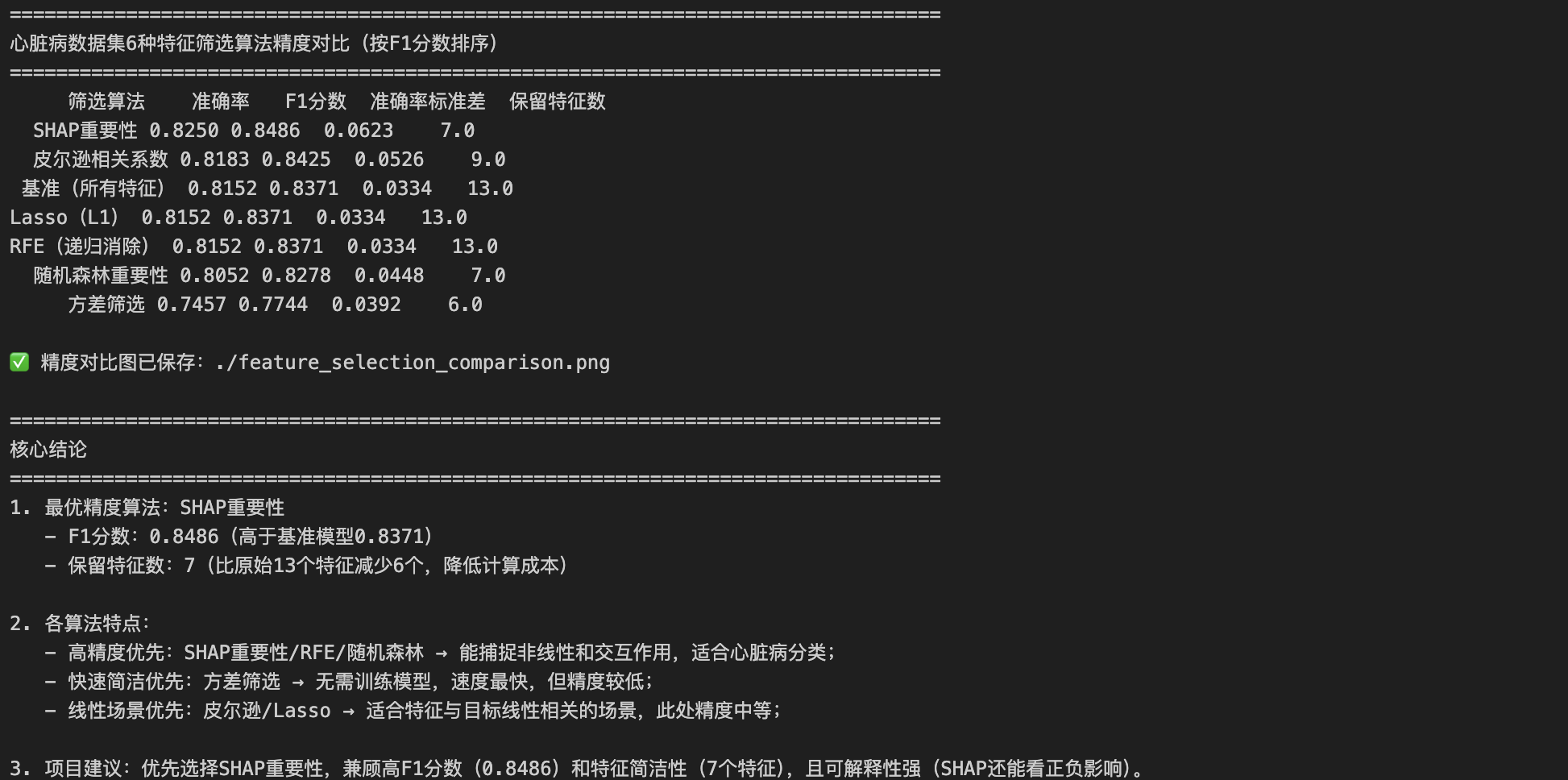
关键结果解读
一、数据结果总结
从第一张图片的表格可提取心脏病数据集 6 种特征筛选算法的核心指标(按 F1 分数排序):
| 筛选算法 | 准确率 | F1 分数 | 准确率标准差 | 保留特征数 |
|---|---|---|---|---|
| SHAP 重要性 | 0.8250 | 0.8486 | 0.0623 | 7 |
| 皮尔逊相关系数 | 0.8183 | 0.8425 | 0.0526 | 9 |
| 基准(所有特征) | 0.8152 | 0.8371 | 0.0334 | 13 |
| Lasso(L1) | 0.8152 | 0.8371 | 0.0334 | 13 |
| RFE(递归消除) | 0.8152 | 0.8371 | 0.0334 | 13 |
| 随机森林重要性 | 0.8052 | 0.8278 | 0.0448 | 7 |
| 方差筛选 | 0.7457 | 0.7744 | 0.0392 | 6 |
二、图表解读
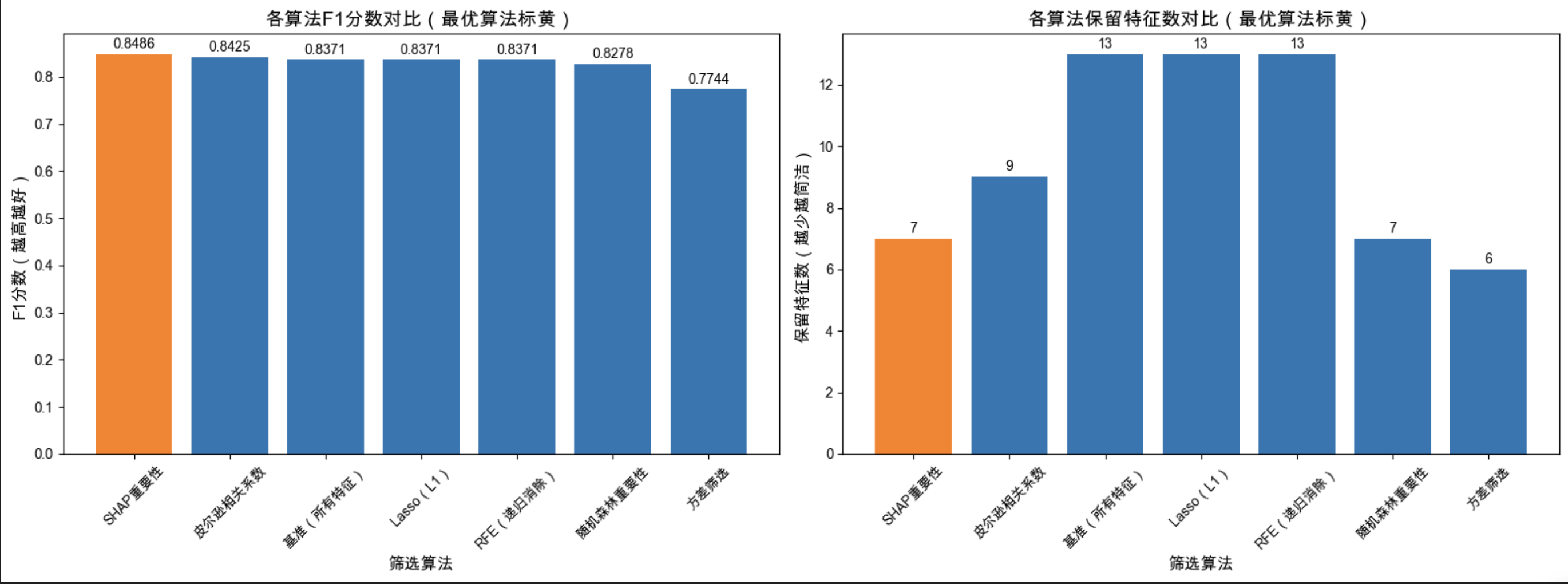
第二张图片的双图对比清晰呈现了算法的性能与精简性:
F1 分数对比(左图):
- SHAP 重要性的 F1 分数(0.8486)显著高于其他算法,是当前最优;
- 皮尔逊相关系数的 F1 分数(0.8425)次之;
- 基准、Lasso、RFE 的 F1 分数一致(0.8371),但未精简特征;
- 方差筛选的 F1 分数最低(0.7744)。
保留特征数对比(右图):
- SHAP 重要性与随机森林重要性均仅保留 7 个特征,在高 F1 分数的同时实现了 46% 的特征精简;
- 基准、Lasso、RFE 未精简特征(保留 13 个),计算成本较高;
- 方差筛选保留特征最少(6 个),但精度损失明显。
三、核心发现
1.最优算法:SHAP 重要性是综合表现最优的方法,同时实现了最高 F1 分数(0.8486)与较高的特征精简率(保留 7 个特征)。
2.算法分层:
- 高精度层:SHAP 重要性、皮尔逊相关系数;
- 均衡层:随机森林重要性(F1 中等,特征精简);
- 低效率层:基准、Lasso、RFE(精度一般且未精简特征);
- 低精度层:方差筛选(特征精简但精度不足)。
3.适用场景:
- 需高精度 + 可解释性:优先选择 SHAP 重要性(可同时输出特征对患病风险的正负影响);
- 需快速粗筛:可选用皮尔逊相关系数(F1 较高,特征精简适中);
- 需极致精简:随机森林重要性(保留 7 个特征,精度略低于 SHAP)。