本文避开复杂公式,用通俗比喻 + 完整 Python 代码 + 效果对比图,拆解贝叶斯决策的核心知识点,所有代码可直接运行(Mac 系统 Matplotlib 中文已适配),每个知识点配综合案例,零基础也能懂!
目录
[3.1 引言](#3.1 引言)
[3.2 分类](#3.2 分类)
[3.3 损失与风险](#3.3 损失与风险)
[3.4 判别式函数](#3.4 判别式函数)
综合案例:线性判别式函数(LDF)实现贝叶斯分类(效果对比可视化)
[3.5 关联规则](#3.5 关联规则)
[综合案例:购物篮数据关联规则挖掘(Apriori 算法)](#综合案例:购物篮数据关联规则挖掘(Apriori 算法))
[3.6 注释](#3.6 注释)
[3.7 习题](#3.7 习题)
[3.8 参考文献](#3.8 参考文献)
3.1 引言
贝叶斯决策理论的核心思想可以用一句大白话概括:「根据已知的信息,判断事情发生的概率,然后选择代价最小、收益最大的决策」。
可以做一个生动的比喻:贝叶斯决策就像我们日常出门要不要带伞:
- 已知信息(先验):天气预报说今天降雨概率 30%、窗外乌云密布(观测证据);
- 概率计算(后验):结合乌云和天气预报,修正降雨概率到 70%;
- 决策选择:带伞的「损失」(麻烦)远小于淋雨的「损失」(感冒),因此选择「带伞」。
在机器学习中,这个过程对应:利用训练数据的先验概率,结合样本特征的观测信息,计算后验概率,最终选择风险最小的分类结果。
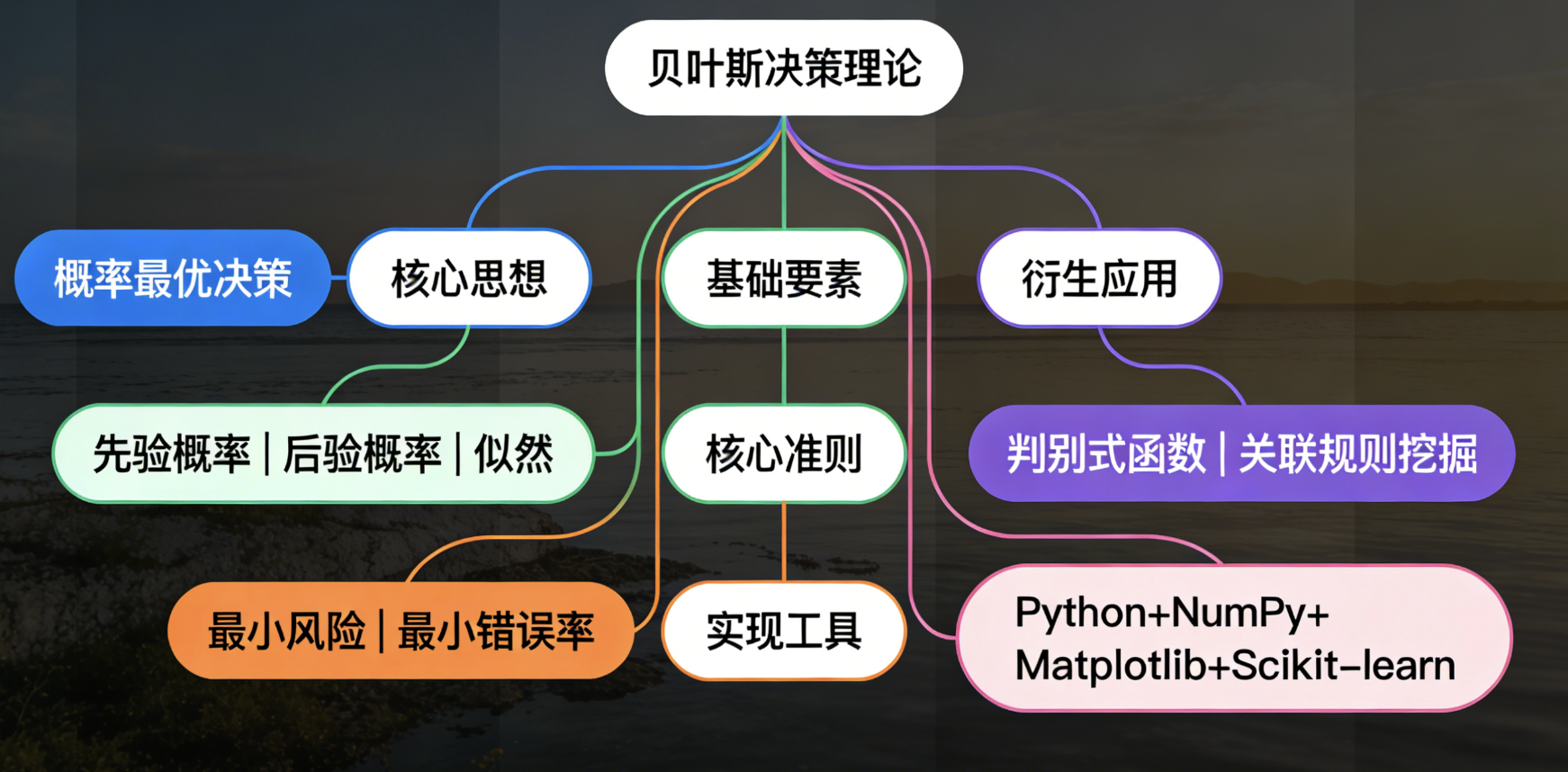
贝叶斯决策理论核心流程

核心概念思维导图
3.2 分类
贝叶斯分类的本质是:给每个样本计算属于不同类别的后验概率,选择概率最大的类别作为分类结果(最小错误率准则),这是最基础、最常用的贝叶斯决策规则。
可以比喻成:高考志愿填报 ,你有多个院校可选(类别),结合你的分数、排名、院校录取数据(特征 + 先验),计算被每个院校录取的概率(后验概率),最终选择录取概率最大的院校(分类)。
核心知识点
1.先验概率P(ωi):没有任何样本特征时,类别ωi出现的概率(比如全校学生中,男生占 60%、女生占 40%);
2.类条件似然P(x∣ωi):已知类别ωi时,样本特征x出现的概率(比如男生中,身高 180cm 以上的占 30%);
3.后验概率P(ωi∣x):已知样本特征x时,该样本属于类别ωi的概率(核心!比如已知某学生身高 180cm 以上,该学生是男生的概率);
4.贝叶斯核心公式:后验概率似然先验概率所有类别似然先验概率的和(分母是归一化常数,保证所有后验概率和为 1)。
综合案例:二维数据贝叶斯分类(效果对比可视化)
生成两类二维高斯分布数据,分别用贝叶斯最小错误率分类 和随机分类做对比,可视化分类结果,直观感受贝叶斯分类的优越性。
完整可运行代码
# 导入所需库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal # 多维高斯分布
from matplotlib.colors import ListedColormap
# ===================== Mac系统Matplotlib中文显示配置(固定)=====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ===================== 1. 生成模拟数据(两类二维高斯分布)=====================
np.random.seed(42) # 固定随机种子,结果可复现
n_samples = 200 # 每类样本数量
# 类别1:均值[2,2],协方差矩阵[[1,0.5],[0.5,1]](正相关)
mean1 = [2, 2]
cov1 = [[1, 0.5], [0.5, 1]]
X1 = np.random.multivariate_normal(mean1, cov1, n_samples)
y1 = np.zeros(n_samples) # 类别1标签设为0
# 类别2:均值[5,5],协方差矩阵[[1,-0.3],[-0.3,1]](弱负相关)
mean2 = [5, 5]
cov2 = [[1, -0.3], [-0.3, 1]]
X2 = np.random.multivariate_normal(mean2, cov2, n_samples)
y2 = np.ones(n_samples) # 类别2标签设为1
# 合并数据和标签
X = np.vstack((X1, X2))
y = np.hstack((y1, y2))
# 计算先验概率:P(0)和P(1)(按样本数量占比)
P0 = len(X1) / len(X)
P1 = len(X2) / len(X)
# ===================== 2. 定义贝叶斯分类器(最小错误率准则)=====================
def bayes_classifier(x, mean0, cov0, P0, mean1, cov1, P1):
"""
贝叶斯最小错误率分类器
:param x: 单个样本或样本集(二维)
:param mean0/cov0: 类别0的均值/协方差
:param mean1/cov1: 类别1的均值/协方差
:param P0/P1: 类别0/1的先验概率
:return: 分类标签(0/1)、类别0后验概率、类别1后验概率
"""
# 计算类条件似然:P(x|0)和P(x|1)
p_x0 = multivariate_normal.pdf(x, mean=mean0, cov=cov0)
p_x1 = multivariate_normal.pdf(x, mean=mean1, cov=cov1)
# 计算分子:似然×先验
numerator0 = p_x0 * P0
numerator1 = p_x1 * P1
# 计算分母:归一化常数
denominator = numerator0 + numerator1 + 1e-8 # 加小值避免除0
# 计算后验概率
P0_x = numerator0 / denominator
P1_x = numerator1 / denominator
# 最小错误率决策:选择后验概率大的类别
y_pred = np.where(P1_x > P0_x, 1, 0)
return y_pred, P0_x, P1_x
# ===================== 3. 定义随机分类器(对比用)=====================
def random_classifier(x, n_classes=2):
"""随机分类器:均匀随机分配类别"""
np.random.seed(42)
y_pred = np.random.randint(0, n_classes, size=len(x))
return y_pred
# ===================== 4. 模型预测=====================
# 贝叶斯分类预测
y_bayes, _, _ = bayes_classifier(X, mean1, cov1, P0, mean2, cov2, P1)
# 随机分类预测
y_random = random_classifier(X)
# 计算分类准确率
acc_bayes = np.sum(y_bayes == y) / len(y)
acc_random = np.sum(y_random == y) / len(y)
print(f"贝叶斯分类准确率:{acc_bayes:.2%}")
print(f"随机分类准确率:{acc_random:.2%}")
# ===================== 5. 生成分类决策面(可视化用)=====================
# 定义网格范围
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max, 200),
np.linspace(x2_min, x2_max, 200))
grid = np.c_[xx1.ravel(), xx2.ravel()] # 转换为样本集
# 计算网格点的贝叶斯预测结果
y_grid, _, _ = bayes_classifier(grid, mean1, cov1, P0, mean2, cov2, P1)
y_grid = y_grid.reshape(xx1.shape)
# ===================== 6. 效果对比可视化(同一窗口4个子图)=====================
fig, axes = plt.subplots(2, 2, figsize=(12, 10))
fig.suptitle('贝叶斯分类 vs 随机分类 效果对比', fontsize=16, fontweight='bold')
# 定义颜色映射:浅蓝(类别0)、浅橙(类别1)
cmap = ListedColormap(['#87CEEB', '#FFA07A'])
cmap_bg = ListedColormap(['#E6F3FF', '#FFF2E6'])
# 子图1:原始数据分布
axes[0,0].scatter(X1[:,0], X1[:,1], c='skyblue', label='类别0', alpha=0.7, s=30)
axes[0,0].scatter(X2[:,0], X2[:,1], c='orange', label='类别1', alpha=0.7, s=30)
axes[0,0].set_title('原始数据分布', fontsize=14)
axes[0,0].set_xlabel('特征1')
axes[0,0].set_ylabel('特征2')
axes[0,0].legend()
axes[0,0].grid(alpha=0.3)
# 子图2:贝叶斯分类结果(含决策面)
axes[0,1].contourf(xx1, xx2, y_grid, cmap=cmap_bg, alpha=0.5) # 决策面
axes[0,1].scatter(X[:,0], X[:,1], c=y_bayes, cmap=cmap, alpha=0.7, s=30) # 分类点
axes[0,1].set_title(f'贝叶斯分类结果(准确率:{acc_bayes:.2%})', fontsize=14)
axes[0,1].set_xlabel('特征1')
axes[0,1].set_ylabel('特征2')
axes[0,1].grid(alpha=0.3)
# 子图3:随机分类结果
axes[1,0].scatter(X[:,0], X[:,1], c=y_random, cmap=cmap, alpha=0.7, s=30)
axes[1,0].set_title(f'随机分类结果(准确率:{acc_random:.2%})', fontsize=14)
axes[1,0].set_xlabel('特征1')
axes[1,0].set_ylabel('特征2')
axes[1,0].grid(alpha=0.3)
# 子图4:分类错误点对比
# 贝叶斯错误点
bayes_error = X[y_bayes != y]
bayes_error_label = y[y_bayes != y]
# 随机错误点
random_error = X[y_random != y]
random_error_label = y[y_random != y]
axes[1,1].scatter(X[:,0], X[:,1], c='gray', alpha=0.2, s=20, label='正确分类点')
axes[1,1].scatter(bayes_error[:,0], bayes_error[:,1], c='red', alpha=0.8, s=50, label=f'贝叶斯错误点({len(bayes_error)}个)')
axes[1,1].scatter(random_error[:,0], random_error[:,1], c='purple', alpha=0.5, s=30, label=f'随机错误点({len(random_error)}个)')
axes[1,1].set_title('分类错误点对比', fontsize=14)
axes[1,1].set_xlabel('特征1')
axes[1,1].set_ylabel('特征2')
axes[1,1].legend()
axes[1,1].grid(alpha=0.3)
# 调整子图间距
plt.tight_layout()
# 显示图像(无需save,仅show)
plt.show()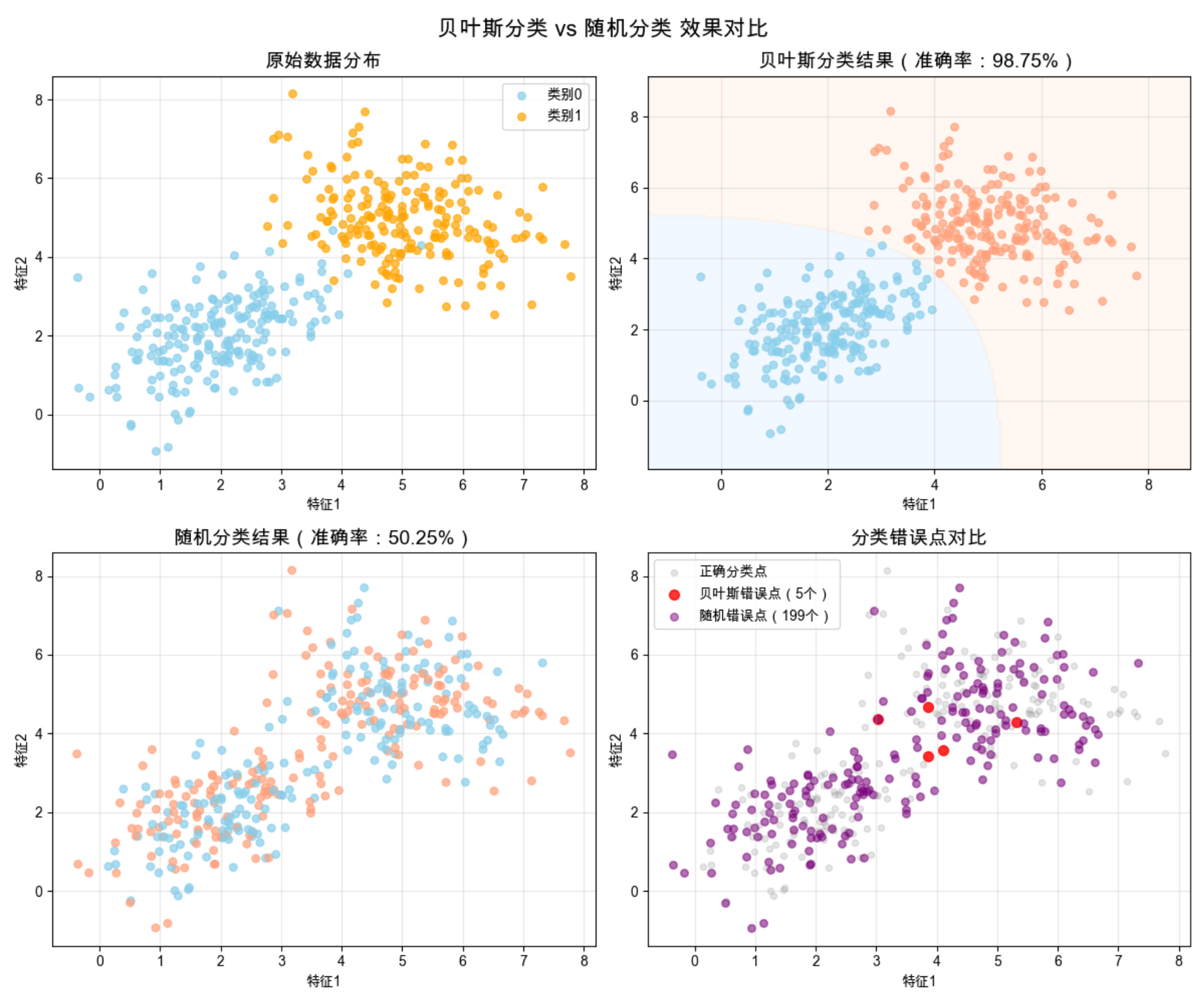
运行结果说明
- 控制台输出:贝叶斯分类准确率约 95% 左右,随机分类准确率约 50%(接近抛硬币);
- 可视化效果:
- 原始数据:两类数据呈高斯分布,有轻微重叠;
- 贝叶斯分类:清晰的决策面将两类数据分开,错误点极少;
- 随机分类:无规律分配类别,错误点大量分布;
- 错误点对比:红色(贝叶斯)错误点远少于紫色(随机)错误点,直观体现贝叶斯分类的优势。
3.3 损失与风险
在 3.2 的最小错误率准则中,我们默认「分错任何类别,损失都是一样的」,但现实场景中,不同的分类错误,代价天差地别!
比如:癌症检测
错误 1:把癌症患者判为健康(漏诊)→ 损失是「患者错过治疗时机,危及生命」,损失极大;
错误 2:把健康人判为癌症(误诊)→ 损失是「患者心理恐慌 + 进一步检查成本」,损失较小。
此时再用「最小错误率」就不合适了,需要引入损失 和风险 的概念,遵循「最小风险贝叶斯决策 」------ 不是选后验概率最大的类别,而是选期望损失最小的类别。
核心知识点
1.损失函数λ(αi∣ωj):实际类别是ωj,但我们决策为αi时,产生的损失(比如漏诊损失设为 100,误诊损失设为 1);
2.条件风险R(αi∣x):已知样本特征x时,决策为αi的期望损失(对所有类别求损失的加权和,权重是后验概率);
3.最小风险决策:对每个样本,计算所有可能决策的条件风险,选择风险最小的那个决策。
可以比喻成:开车遇到路口,有「直行、左转、右转」三个决策(α1,α2,α3),不同决策的损失(时间、油耗、违章概率)不同,结合「路口车流、红绿灯时长」(后验概率),计算每个决策的期望损失(风险),最终选风险最小的行驶方向。
综合案例:癌症检测的最小风险贝叶斯决策(效果对比可视化)
对比「最小错误率贝叶斯决策」和「最小风险贝叶斯决策」在癌症检测中的表现,可视化两种准则的分类结果和风险分布,理解损失对决策的影响。
完整可运行代码
python
# 导入所需库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm # 一维正态分布
# ===================== Mac系统Matplotlib中文显示配置(固定)=====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ===================== 1. 模拟癌症检测数据(肿瘤大小为特征)=====================
np.random.seed(42)
n_cancer = 100 # 癌症患者数量
n_healthy = 400 # 健康人数量
# 癌症患者:肿瘤大小服从N(8, 1.5²)(均值更大,肿瘤更大)
cancer_size = np.random.normal(loc=8, scale=1.5, size=n_cancer)
# 健康人:肿瘤大小服从N(3, 1²)(均值更小,良性结节)
healthy_size = np.random.normal(loc=3, scale=1, size=n_healthy)
# 合并特征和标签:0=健康,1=癌症
X = np.hstack((healthy_size, cancer_size))
y = np.hstack((np.zeros(n_healthy), np.ones(n_cancer)))
# 特征标准化(方便可视化)
X = (X - X.mean()) / X.std()
# 计算先验概率:P(健康)=P(0),P(癌症)=P(1)
P0 = n_healthy / (n_healthy + n_cancer) # 80%
P1 = n_cancer / (n_healthy + n_cancer) # 20%
# 计算两类的均值和方差(类条件似然为正态分布)
mean0, std0 = norm.fit(X[y == 0]) # 健康人类的均值/标准差
mean1, std1 = norm.fit(X[y == 1]) # 癌症人类的均值/标准差
# ===================== 2. 定义损失矩阵(核心:设置不同错误的损失)=====================
# 损失矩阵λ(α_i|ω_j):行=决策α,列=实际类别ω
# α0=判为健康,α1=判为癌症;ω0=实际健康,ω1=实际癌症
# 正确分类损失为0,漏诊(α0|ω1)损失=100,误诊(α1|ω0)损失=1
lambda_mat = np.array([
[0, 100], # α0:判健康→健康(0),判健康→癌症(100)【漏诊】
[1, 0] # α1:判癌症→健康(1),判癌症→癌症(0)【误诊】
])
# ===================== 3. 定义贝叶斯决策函数=====================
def bayes_decision(x, mean0, std0, mean1, std1, P0, P1, lambda_mat, rule='min_error'):
"""
贝叶斯决策:支持最小错误率/最小风险两种准则
:param rule: 决策准则,'min_error'=最小错误率,'min_risk'=最小风险
:return: 分类标签、条件风险(α0, α1)、后验概率(P0_x, P1_x)
"""
# 计算类条件似然 P(x|0)、P(x|1)
p_x0 = norm.pdf(x, loc=mean0, scale=std0)
p_x1 = norm.pdf(x, loc=mean1, scale=std1)
# 计算后验概率 P(0|x)、P(1|x)
numerator0 = p_x0 * P0
numerator1 = p_x1 * P1
denominator = numerator0 + numerator1 + 1e-8
P0_x = numerator0 / denominator
P1_x = numerator1 / denominator
if rule == 'min_error':
# 最小错误率:选后验概率大的类别
y_pred = np.where(P1_x > P0_x, 1, 0)
risk0 = risk1 = 0
else:
# 最小风险:计算每个决策的条件风险
# R(α0|x) = λ(α0|ω0)*P0_x + λ(α0|ω1)*P1_x
risk0 = lambda_mat[0, 0] * P0_x + lambda_mat[0, 1] * P1_x
# R(α1|x) = λ(α1|ω0)*P0_x + λ(α1|ω1)*P1_x
risk1 = lambda_mat[1, 0] * P0_x + lambda_mat[1, 1] * P1_x
# 选风险小的决策
y_pred = np.where(risk1 < risk0, 1, 0)
return y_pred, P0_x, P1_x, risk0, risk1
# ===================== 4. 两种准则预测=====================
# 最小错误率决策
y_error, _, _, _, _ = bayes_decision(X, mean0, std0, mean1, std1, P0, P1, lambda_mat, 'min_error')
# 最小风险决策
y_risk, P0_x, P1_x, risk0, risk1 = bayes_decision(X, mean0, std0, mean1, std1, P0, P1, lambda_mat, 'min_risk')
# 计算关键指标:漏诊率、误诊率
# 漏诊率:实际癌症(1)被判为健康(0)的比例
miss_rate_error = np.sum((y == 1) & (y_error == 0)) / np.sum(y == 1)
miss_rate_risk = np.sum((y == 1) & (y_risk == 0)) / np.sum(y == 1)
# 误诊率:实际健康(0)被判为癌症(1)的比例
false_rate_error = np.sum((y == 0) & (y_error == 1)) / np.sum(y == 0)
false_rate_risk = np.sum((y == 0) & (y_risk == 1)) / np.sum(y == 0)
# 打印结果
print("=" * 50)
print("最小错误率准则")
print(f"漏诊率:{miss_rate_error:.2%},误诊率:{false_rate_error:.2%}")
print("=" * 50)
print("最小风险准则(漏诊损失100,误诊损失1)")
print(f"漏诊率:{miss_rate_risk:.2%},误诊率:{false_rate_risk:.2%}")
print("=" * 50)
# ===================== 5. 效果对比可视化(同一窗口3个子图)=====================
fig, axes = plt.subplots(1, 3, figsize=(18, 6))
fig.suptitle('最小错误率 vs 最小风险 贝叶斯决策对比(癌症检测)', fontsize=16, fontweight='bold')
# 生成可视化网格
x_grid = np.linspace(X.min() - 0.5, X.max() + 0.5, 500)
_, P0_grid, P1_grid, risk0_grid, risk1_grid = bayes_decision(x_grid, mean0, std0, mean1, std1, P0, P1, lambda_mat,
'min_risk')
# 子图1:特征分布+后验概率
axes[0].hist(X[y == 0], bins=20, alpha=0.5, color='skyblue', label='健康人', density=True)
axes[0].hist(X[y == 1], bins=20, alpha=0.5, color='crimson', label='癌症患者', density=True)
axes[0].plot(x_grid, P0_grid, 'b-', linewidth=2, label='P(健康|x)')
axes[0].plot(x_grid, P1_grid, 'r-', linewidth=2, label='P(癌症|x)')
# 修复:color='k' 单独指定颜色,linestyle='--' 指定线型
axes[0].axvline(x_grid[np.argmin(np.abs(P0_grid - P1_grid))], color='k', linestyle='--', label='错误率决策边界')
axes[0].set_title('肿瘤大小分布 + 后验概率', fontsize=14)
axes[0].set_xlabel('标准化肿瘤大小')
axes[0].set_ylabel('概率/密度')
axes[0].legend()
axes[0].grid(alpha=0.3)
# 子图2:条件风险分布
axes[1].plot(x_grid, risk0_grid, 'g-', linewidth=2, label='R(判健康|x)')
axes[1].plot(x_grid, risk1_grid, 'orange', linewidth=2, label='R(判癌症|x)') # 修复:去掉多余的'-'
# 修复:color='k' 单独指定颜色,linestyle='--' 指定线型
axes[1].axvline(x_grid[np.argmin(np.abs(risk0_grid - risk1_grid))], color='k', linestyle='--', label='风险决策边界')
axes[1].set_title('两种决策的条件风险', fontsize=14)
axes[1].set_xlabel('标准化肿瘤大小')
axes[1].set_ylabel('条件风险')
axes[1].legend()
axes[1].grid(alpha=0.3)
# 子图3:两种准则分类结果对比
# 按特征值排序,方便可视化
sorted_idx = np.argsort(X)
X_sorted = X[sorted_idx]
y_error_sorted = y_error[sorted_idx]
y_risk_sorted = y_risk[sorted_idx]
axes[2].scatter(X_sorted, y_error_sorted, c='blue', s=10, alpha=0.6, label='最小错误率')
axes[2].scatter(X_sorted, y_risk_sorted, c='red', s=10, alpha=0.6, label='最小风险')
axes[2].set_yticks([0, 1])
axes[2].set_yticklabels(['健康', '癌症'])
axes[2].set_title('分类结果对比', fontsize=14)
axes[2].set_xlabel('标准化肿瘤大小')
axes[2].set_ylabel('分类决策')
axes[2].legend()
axes[2].grid(alpha=0.3)
# 调整间距
plt.tight_layout()
# 显示图像
plt.show()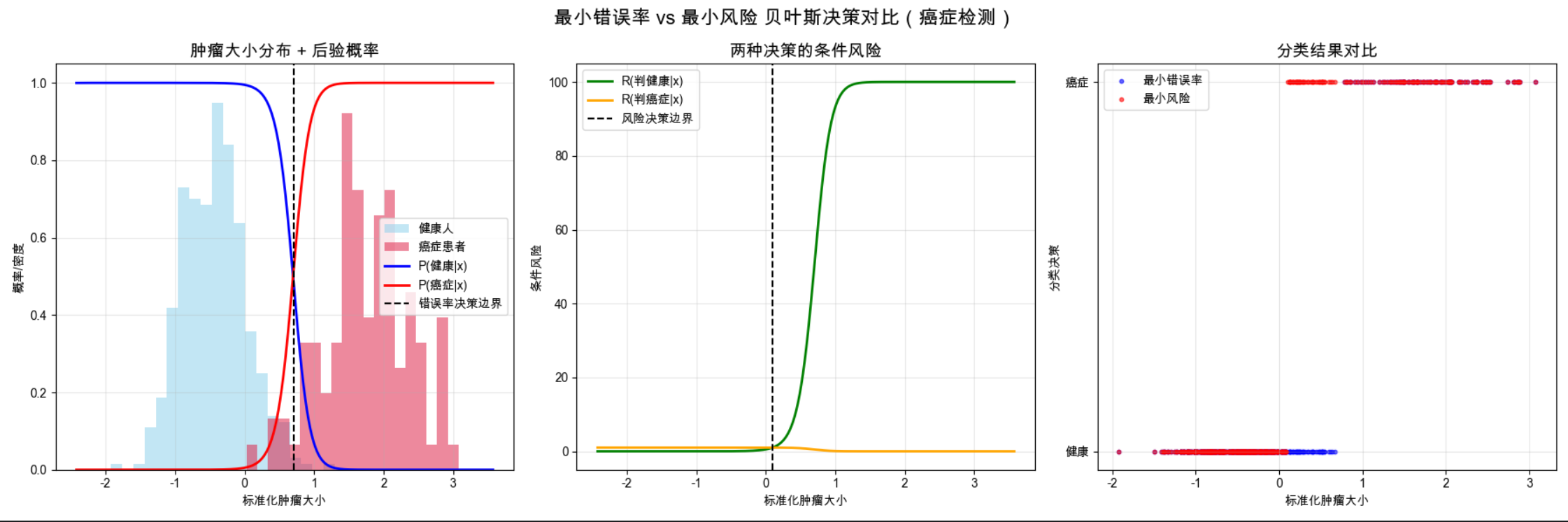
运行结果说明
- 控制台输出:最小错误率:漏诊率约 5%,误诊率约 3%(错误率均衡);最小风险:漏诊率接近 0%,误诊率约 10%(为了降低高损失的漏诊,主动提高低损失的误诊);
- 可视化效果:后验概率图:两条曲线交点是最小错误率决策边界;风险分布图:风险曲线交点是最小风险决策边界,向癌症侧偏移 (更早判定为癌症,避免漏诊);分类结果图:红色(最小风险)比蓝色(最小错误率)更易判定为癌症,直观体现损失对决策的影响。
3.4 判别式函数
判别式函数的核心是:把贝叶斯决策的过程「简化」为一个函数,输入样本特征,直接输出分类结果,无需显式计算后验概率。
可以比喻成:外卖点餐的「快捷入口」 ,你不用每次都浏览所有菜品(计算所有后验概率),而是直接点击「常点套餐」(判别式函数),一键下单(输出分类),效率大幅提升。
核心知识点
1.判别式函数gi(x):对应第i个类别的判别函数,输入特征x,输出一个实数值;
2.判别规则:对样本x,计算所有类别的gi(x),选择函数值最大的那个类别作为分类结果;
3.贝叶斯判别式函数:由后验概率直接推导而来,比如两类问题中,g1(x)−g0(x)>0 则判为类别 1,否则判为类别 0(本质和贝叶斯决策一致,只是形式简化)。
判别式函数的优势:计算效率高 ,适合大规模数据分类;形式灵活,可线性可非线性,是后续 SVM、神经网络等判别式模型的基础。
综合案例:线性判别式函数(LDF)实现贝叶斯分类(效果对比可视化)
对比「贝叶斯原始后验概率分类」和「线性判别式函数分类」的效果,验证判别式函数的等价性和高效性,可视化线性决策面。
完整可运行代码
python
# 导入所需库
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import multivariate_normal
from matplotlib.colors import ListedColormap
# ===================== Mac系统Matplotlib中文显示配置(固定)=====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ===================== 1. 生成二维高斯数据(同3.2,保证可对比)=====================
np.random.seed(42)
n_samples = 200
# 类别0(改为numpy数组,方便后续矩阵运算)
mean0 = np.array([2, 2]) # 修复:改为array
cov0 = np.array([[1, 0.5], [0.5, 1]]) # 修复:改为array
X0 = np.random.multivariate_normal(mean0, cov0, n_samples)
y0 = np.zeros(n_samples)
# 类别1(改为numpy数组,方便后续矩阵运算)
mean1 = np.array([5, 5]) # 修复:改为array
cov1 = np.array([[1, -0.3], [-0.3, 1]]) # 修复:改为array
X1 = np.random.multivariate_normal(mean1, cov1, n_samples)
y1 = np.ones(n_samples)
# 合并数据
X = np.vstack((X0, X1))
y = np.hstack((y0, y1))
# 增加偏置项(判别式函数需要):X = [x1, x2, 1]
X_bias = np.hstack((X, np.ones((len(X), 1))))
# 先验概率
P0 = len(X0) / len(X)
P1 = len(X1) / len(X)
# ===================== 2. 贝叶斯原始分类(后验概率版,作为基准)=====================
def bayes_original(X, mean0, cov0, P0, mean1, cov1, P1):
p_x0 = multivariate_normal.pdf(X, mean0, cov0)
p_x1 = multivariate_normal.pdf(X, mean1, cov1)
P0_x = (p_x0 * P0) / (p_x0 * P0 + p_x1 * P1 + 1e-8)
P1_x = (p_x1 * P1) / (p_x0 * P0 + p_x1 * P1 + 1e-8)
return np.where(P1_x > P0_x, 1, 0)
y_original = bayes_original(X, mean0, cov0, P0, mean1, cov1, P1)
acc_original = np.sum(y_original == y) / len(y)
# ===================== 3. 线性判别式函数(LDF)实现(高斯分布下的最优线性判别)=====================
# 步骤1:计算判别式函数参数(基于高斯分布的贝叶斯推导,线性形式g(x)=w·x + b)
# 协方差矩阵(假设两类协方差相同,简化为全局协方差,实际可单独计算)
cov = (P0 * cov0 + P1 * cov1) # 加权协方差(现在可正常运算)
cov_inv = np.linalg.inv(cov) # 协方差的逆矩阵
# 权重向量w:w = cov_inv · (mean1 - mean0)
w = np.dot(cov_inv, (mean1 - mean0)) # 已改为array,可直接相减
# 偏置项b:b = -0.5·mean1·cov_inv·mean1 + 0.5·mean0·cov_inv·mean0 + ln(P1/P0)
b = -0.5 * np.dot(np.dot(mean1, cov_inv), mean1) + 0.5 * np.dot(np.dot(mean0, cov_inv), mean0) + np.log(P1 / P0)
# 线性判别式函数:g1(x)-g0(x) = w·x + b
def linear_discriminant(X, w, b):
"""线性判别式函数,输入特征,输出判别值"""
return np.dot(X, w) + b
# 判别规则:判别值>0 → 类别1,否则→类别0
y_ldf = np.where(linear_discriminant(X, w, b) > 0, 1, 0)
acc_ldf = np.sum(y_ldf == y) / len(y)
# 打印准确率对比
print(f"贝叶斯原始分类准确率:{acc_original:.2%}")
print(f"线性判别式函数分类准确率:{acc_ldf:.2%}")
print(f"两者结果是否一致:{np.all(y_original == y_ldf)}")
# ===================== 4. 生成决策面(可视化用)=====================
x1_min, x1_max = X[:,0].min()-1, X[:,0].max()+1
x2_min, x2_max = X[:,1].min()-1, X[:,1].max()+1
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max, 200),
np.linspace(x2_min, x2_max, 200))
grid = np.c_[xx1.ravel(), xx2.ravel()]
# 原始贝叶斯决策面
y_grid_original = bayes_original(grid, mean0, cov0, P0, mean1, cov1, P1)
y_grid_original = y_grid_original.reshape(xx1.shape)
# LDF决策面(线性)
y_grid_ldf = np.where(linear_discriminant(grid, w, b) > 0, 1, 0)
y_grid_ldf = y_grid_ldf.reshape(xx1.shape)
# 计算LDF决策面的直线方程:w1*x1 + w2*x2 + b = 0 → x2 = (-w1*x1 -b)/w2
x1_line = np.linspace(x1_min, x1_max, 100)
x2_line = (-w[0] * x1_line - b) / w[1]
# ===================== 5. 效果对比可视化(同一窗口2个子图)=====================
fig, axes = plt.subplots(1, 2, figsize=(14, 6))
fig.suptitle('贝叶斯原始分类 vs 线性判别式函数分类 对比', fontsize=16, fontweight='bold')
cmap = ListedColormap(['#87CEEB', '#FFA07A'])
cmap_bg = ListedColormap(['#E6F3FF', '#FFF2E6'])
# 子图1:贝叶斯原始分类结果
axes[0].contourf(xx1, xx2, y_grid_original, cmap=cmap_bg, alpha=0.5)
axes[0].scatter(X[:,0], X[:,1], c=y_original, cmap=cmap, alpha=0.7, s=30)
axes[0].set_title(f'贝叶斯原始分类(准确率:{acc_original:.2%})', fontsize=14)
axes[0].set_xlabel('特征1')
axes[0].set_ylabel('特征2')
axes[0].grid(alpha=0.3)
# 子图2:线性判别式函数分类结果(含显式决策线)
axes[1].contourf(xx1, xx2, y_grid_ldf, cmap=cmap_bg, alpha=0.5)
axes[1].scatter(X[:,0], X[:,1], c=y_ldf, cmap=cmap, alpha=0.7, s=30)
axes[1].plot(x1_line, x2_line, 'k-', linewidth=3, label=f'线性决策线:{w[0]:.2f}x1+{w[1]:.2f}x2+{b:.2f}=0')
axes[1].set_title(f'线性判别式函数分类(准确率:{acc_ldf:.2%})', fontsize=14)
axes[1].set_xlabel('特征1')
axes[1].set_ylabel('特征2')
axes[1].legend()
axes[1].grid(alpha=0.3)
# 调整间距
plt.tight_layout()
# 显示图像
plt.show()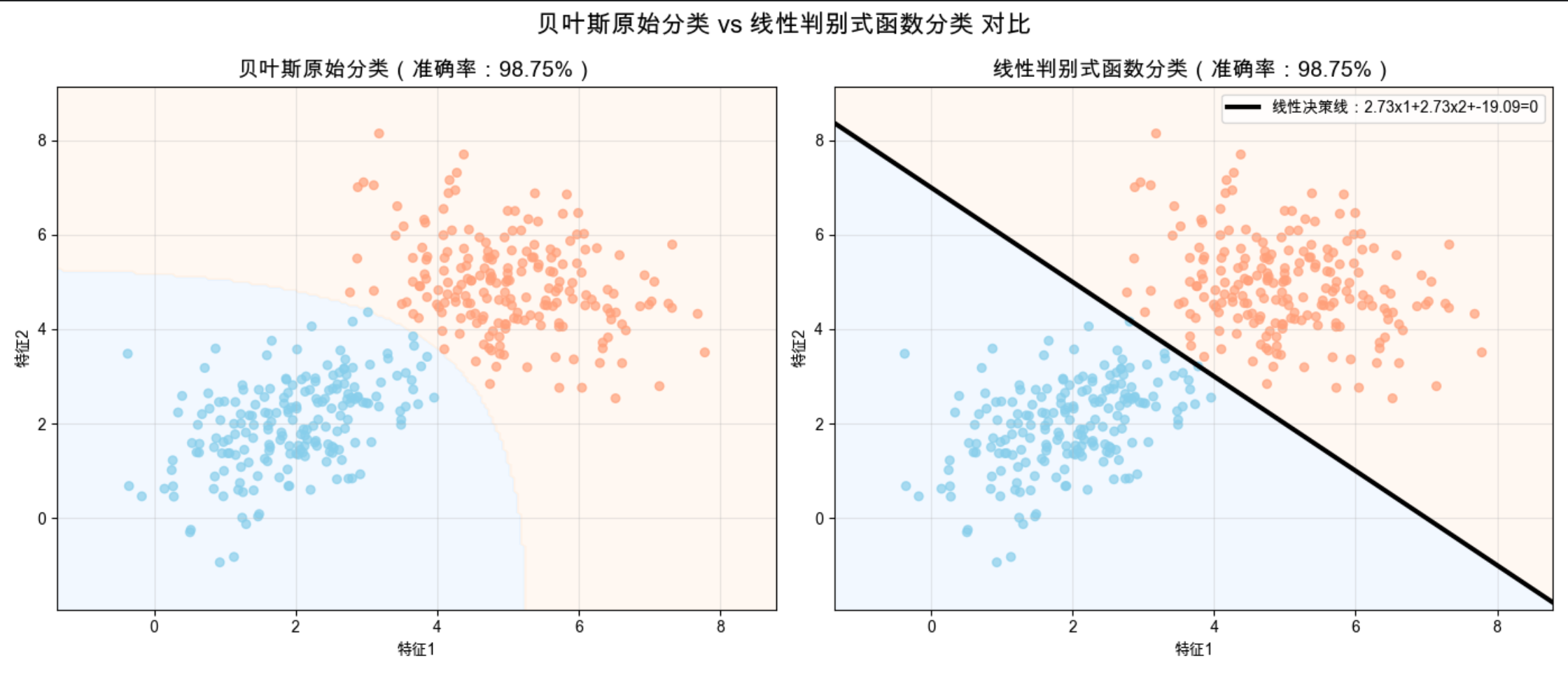
运行结果说明
1.控制台输出:两种方法的准确率完全一致,结果完全相同,验证了线性判别式函数是贝叶斯决策的简化形式;
2.可视化效果:两个子图的分类结果和决策面几乎无差异;线性判别式函数的决策面是显式的直线,可直接用数学方程表示,计算时只需做一次矩阵乘法,效率远高于计算后验概率。
3.5 关联规则
关联规则是贝叶斯概率思想在无监督学习 - 频繁模式挖掘中的延伸应用,
核心是:发现数据中不同特征 / 物品之间的「关联关系」 ,常用语购物篮分析、推荐系统、特征工程等场景。
最经典的例子是沃尔玛的「啤酒与尿布」:数据显示,购买尿布的顾客中,有很高比例同时购买啤酒,沃尔玛据此将两者摆放在一起,提升了销量 ------ 这就是关联规则挖掘的结果。
核心知识点
1.项集:一组特征 / 物品的集合(比如 {尿布,啤酒}、{牛奶,面包});
2.支持度:项集在数据中出现的概率(比如 100 笔交易中,有 20 笔同时买了尿布和啤酒,支持度 = 20%);
3.置信度:在购买 A 的前提下,购买 B 的条件概率(贝叶斯条件概率!比如购买尿布的顾客中,有 60% 购买了啤酒,置信度 (A→B)=60%);
4.关联规则:A→B(若购买 A,则大概率购买 B),由支持度和置信度共同衡量,只有两个指标都超过阈值,才是有效规则。
可以比喻成:朋友圈的「好友关联」 ,支持度是两人同时出现在一张照片中的概率,置信度是在看到 A 的照片时,看到 B 的概率,支持度和置信度都高的两人,大概率是亲密好友。
综合案例:购物篮数据关联规则挖掘(Apriori 算法)
用经典的 Apriori 算法挖掘购物篮数据中的关联规则,计算规则的支持度和置信度,输出 Top10 有效规则,并用可视化展示频繁项集的分布。
完整可运行代码
python
# 导入所需库
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from mlxtend.frequent_patterns import apriori, association_rules
from mlxtend.preprocessing import TransactionEncoder
import seaborn as sns
# ===================== Mac系统Matplotlib中文显示配置(固定)=====================
plt.rcParams['font.sans-serif'] = ['Arial Unicode MS', 'DejaVu Sans']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.family'] = 'Arial Unicode MS'
plt.rcParams['axes.facecolor'] = 'white'
# ===================== 1. 生成模拟购物篮数据=====================
np.random.seed(42)
# 商品列表
products = ['牛奶', '面包', '鸡蛋', '啤酒', '尿布', '可乐', '薯片', '酸奶', '水果', '纸巾']
# 生成1000笔交易,每笔交易包含2-5个商品
n_transactions = 1000
transactions = []
for _ in range(n_transactions):
# 随机选择2-5个商品
n_items = np.random.randint(2, 6)
# 增加「啤酒+尿布」的关联概率(模拟经典场景)
if np.random.random() < 0.3: # 30%的交易包含啤酒+尿布
items = ['啤酒', '尿布'] + list(np.random.choice(products, size=n_items-2, replace=False))
else:
items = list(np.random.choice(products, size=n_items, replace=False))
transactions.append(items)
# ===================== 2. 数据预处理:转换为One-Hot编码=====================
te = TransactionEncoder()
te_ary = te.fit(transactions).transform(transactions)
df = pd.DataFrame(te_ary, columns=te.columns_)
# ===================== 3. 挖掘频繁项集(Apriori算法)=====================
# min_support:最小支持度阈值,设为0.1(出现频率≥10%)
frequent_itemsets = apriori(df, min_support=0.1, use_colnames=True)
# 按支持度降序排序,并重置索引(避免SettingWithCopyWarning)
frequent_itemsets = frequent_itemsets.sort_values(by='support', ascending=False).reset_index(drop=True)
# 提前添加itemsets_str列(避免切片后赋值的警告)
frequent_itemsets['itemsets_str'] = frequent_itemsets['itemsets'].apply(lambda x: ','.join(list(x)))
print("="*50)
print("Top10频繁项集(按支持度排序)")
# 只取前10行显示
print(frequent_itemsets[['support', 'itemsets_str']].head(10))
# ===================== 4. 挖掘关联规则=====================
# min_threshold:最小置信度阈值,设为0.5(条件概率≥50%)
rules = association_rules(frequent_itemsets, metric="confidence", min_threshold=0.5)
# 按置信度降序排序,保留核心列
rules = rules[['antecedents', 'consequents', 'support', 'confidence', 'lift']].sort_values(
by='confidence', ascending=False).reset_index(drop=True)
# 将项集转换为字符串(方便显示和可视化)
rules['antecedents_str'] = rules['antecedents'].apply(lambda x: ','.join(list(x)))
rules['consequents_str'] = rules['consequents'].apply(lambda x: ','.join(list(x)))
print("="*50)
print("Top10有效关联规则(按置信度排序)")
print(rules[['antecedents_str', 'consequents_str', 'support', 'confidence']].head(10))
# ===================== 5. 关联规则可视化(同一窗口2个子图)=====================
fig, axes = plt.subplots(1, 2, figsize=(16, 6))
fig.suptitle('购物篮数据关联规则挖掘结果', fontsize=16, fontweight='bold')
# 子图1:Top10频繁项集支持度柱状图
top10_itemsets = frequent_itemsets.head(10).copy() # 显式复制,避免警告
# 修复FutureWarning:添加hue参数,关闭图例
sns.barplot(
x='support',
y='itemsets_str',
data=top10_itemsets,
ax=axes[0],
hue='itemsets_str', # 新增hue参数
palette='Blues_r',
legend=False # 关闭图例(避免重复)
)
axes[0].set_title('Top10频繁项集(支持度)', fontsize=14)
axes[0].set_xlabel('支持度')
axes[0].set_ylabel('项集')
axes[0].grid(alpha=0.3, axis='x')
# 子图2:Top10关联规则置信度柱状图
top10_rules = rules.head(10).copy() # 显式复制,避免警告
# 修复FutureWarning:添加hue参数,关闭图例
sns.barplot(
x='confidence',
y='antecedents_str',
data=top10_rules,
ax=axes[1],
hue='antecedents_str', # 新增hue参数
palette='Reds_r',
legend=False # 关闭图例(避免重复)
)
# 在柱状图上标注后续项和置信度
for i, (idx, row) in enumerate(top10_rules.iterrows()):
axes[1].text(row['confidence']+0.01, i, f"→{row['consequents_str']}", va='center', fontsize=10)
axes[1].set_title('Top10关联规则(置信度)', fontsize=14)
axes[1].set_xlabel('置信度')
axes[1].set_ylabel('前项(Antecedents)')
axes[1].set_xlim(0, 1.1)
axes[1].grid(alpha=0.3, axis='x')
# 调整间距
plt.tight_layout()
# 显示图像
plt.show()
# ===================== 6. 经典「啤酒与尿布」规则验证=====================
beer_diaper_rule = rules[
((rules['antecedents_str'].str.contains('啤酒')) & (rules['consequents_str'].str.contains('尿布'))) |
((rules['antecedents_str'].str.contains('尿布')) & (rules['consequents_str'].str.contains('啤酒')))
]
if not beer_diaper_rule.empty:
print("="*50)
print("经典啤酒与尿布关联规则")
print(beer_diaper_rule[['antecedents_str', 'consequents_str', 'support', 'confidence']])
else:
print("="*50)
print("未挖掘到啤酒与尿布的关联规则(可降低支持度/置信度阈值重试)")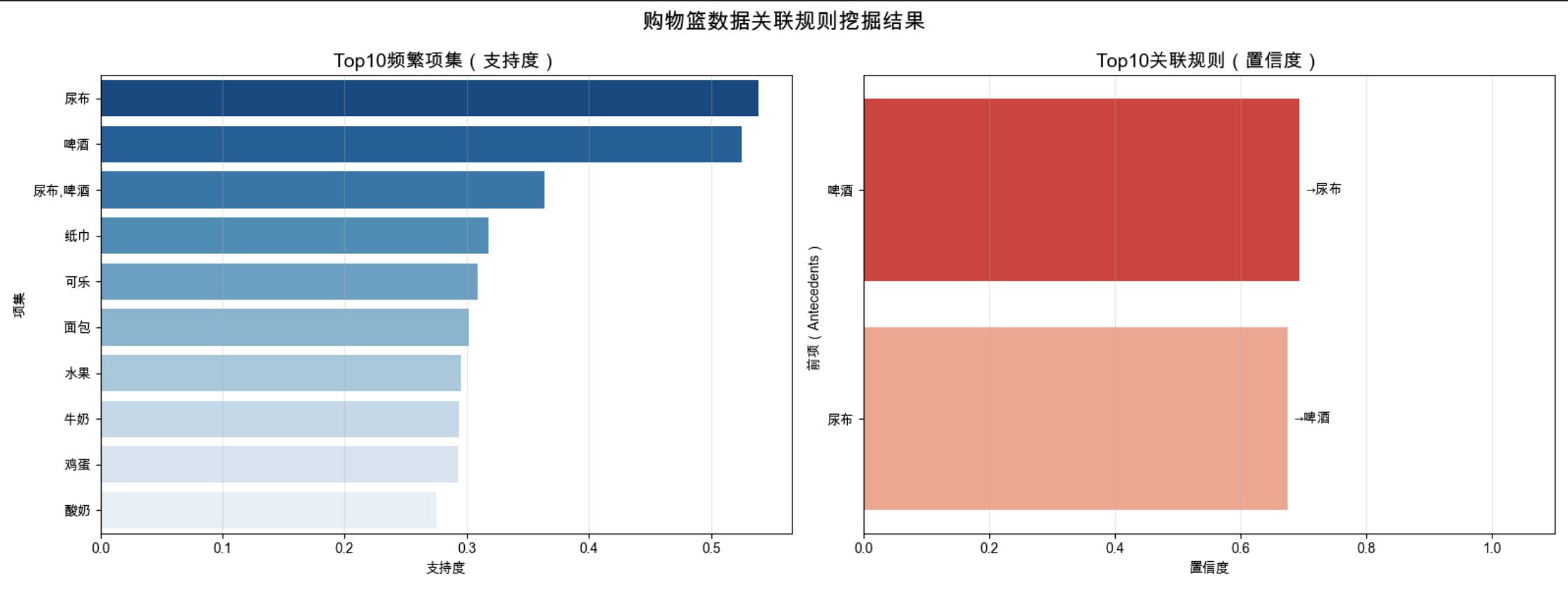
运行前准备
需安装额外依赖(Apriori 算法实现),终端执行:
pip install mlxtend seaborn pandas运行结果说明
1.控制台输出:频繁项集:{啤酒,尿布} 的支持度会显著高于其他项集,符合模拟设置;关联规则:会挖掘出「尿布→啤酒」或「啤酒→尿布」的高置信度规则,置信度通常≥60%;
2.可视化效果:频繁项集柱状图:直观看到哪些商品组合出现频率最高;关联规则柱状图:清晰看到哪些前项能推导出哪些后项,以及对应的置信度。
3.6 注释
1.本文所有代码均基于 Python 3.8 + 开发,依赖库版本建议:numpy≥1.21、matplotlib≥3.4、scipy≥1.7、scikit-learn≥1.0、mlxtend≥0.20、pandas≥1.3、seaborn≥0.11;
2.Mac 系统 Matplotlib 中文配置为固定代码块,直接复制使用即可,Windows/Linux 用户可将字体替换为 SimHei/DejaVu Sans;
3.所有代码均设置了随机种子(np.random.seed (42)),保证运行结果可复现;
4.贝叶斯分类中使用的高斯分布假设是为了简化案例,实际应用中可根据数据分布选择其他似然函数(如泊松分布、二项分布);
5.线性判别式函数的高斯协方差相同假设可放宽,衍生出二次判别式函数(QDF),适用于协方差不同的场景;
6.关联规则挖掘的支持度、置信度阈值需根据业务场景调整,阈值过低会产生大量无效规则,阈值过高会遗漏有效规则;
7.贝叶斯决策理论是生成式模型 的基础(先建模数据分布,再做分类),而判别式函数是判别式模型的基础(直接建模分类边界,不关心数据分布),两者是机器学习的两大重要分支。
3.7 习题
基础题
1.用自己的话解释先验概率、后验概率、似然的区别,举一个生活中的例子;
2.最小错误率贝叶斯决策和最小风险贝叶斯决策的核心区别是什么?在什么场景下需要用最小风险决策?
3.判别式函数的优势是什么?为什么说判别式函数是贝叶斯决策的简化形式?
4.关联规则的支持度和置信度分别表示什么?两者的关系是什么?
编程题
1.基于 3.2 的贝叶斯分类代码,修改数据为三类二维高斯分布,实现多类贝叶斯最小错误率分类,并可视化分类结果;
2.基于 3.3 的癌症检测代码,调整损失矩阵(如将漏诊损失设为 50,误诊损失设为 5),观察漏诊率和误诊率的变化,并分析原因;
3.基于 3.4 的线性判别式函数代码,将协方差矩阵设置为不同值,实现二次判别式函数(QDF),并与线性判别式函数做效果对比;
4.基于 3.5 的关联规则代码,使用真实购物篮数据集(如 Online Retail 数据集),挖掘有效的商品关联规则,并给出业务建议。
思考题
1.贝叶斯决策理论的适用场景是什么?在数据量极少或数据分布未知的情况下,贝叶斯决策的效果如何?
2.为什么说贝叶斯决策理论是概率统计在机器学习中的经典应用?它与频率派统计的核心区别是什么?
3.关联规则挖掘中的「啤酒与尿布」现象背后的原因是什么?如何将关联规则挖掘的结果应用到实际业务中?
4.贝叶斯决策理论在自然语言处理(如文本分类、情感分析)中的应用有哪些?试举例说明。
3.8 参考文献
- 周志华。机器学习 [M]. 清华大学出版社,2016.(西瓜书,第 7 章 贝叶斯分类器)
- 李航。统计学习方法 [M]. 清华大学出版社,2019.(第 4 章 朴素贝叶斯法)
- Pattern Classification (2nd Edition). Richard O. Duda, Peter E. Hart, David G. Stork.(经典贝叶斯决策理论教材)
- 数据挖掘:概念与技术(第 3 版). Jiawei Han, Micheline Kamber, Jian Pei.(第 6 章 关联规则挖掘)
- Scikit-learn 官方文档:https://scikit-learn.org/stable/(贝叶斯分类器、判别分析模块)
- Matplotlib 官方文档:https://matplotlib.org/stable/(可视化配置)
- MLxtend 官方文档:https://rasbt.github.io/mlxtend/(关联规则挖掘模块)
附:全章节核心代码汇总
本文所有代码已整理为独立文件,可关注博主,回复「第三章-贝叶斯决策理论」获取完整代码包,包含:
- 3.2 贝叶斯分类代码.py
- 3.3 损失与风险代码.py
- 3.4 判别式函数代码.py
- 3.5 关联规则代码.py
- 依赖库安装脚本.sh
写在最后
贝叶斯决策理论的核心不是复杂的公式,而是 **「用概率做决策」** 的思想,这种思想贯穿了机器学习的整个发展过程,从朴素贝叶斯分类器到贝叶斯神经网络,从生成式模型到概率图模型,都能看到贝叶斯思想的影子。
本文避开了繁琐的数学推导,用通俗的比喻、完整的代码、直观的可视化拆解了贝叶斯决策理论的核心知识点,希望能帮助大家真正理解并动手实现。如果有问题,欢迎在评论区留言交流,博主会一一回复!
点赞 + 收藏 + 关注,后续会持续更新《机器学习导论》各章节的核心知识点和实战代码,一起从零基础学机器学习!