LeetCode----200.岛屿数量（Medium）

2025/8/18

题目（Medium）：

我的思路：

直观看起来，每一个陆地都可以是一个岛屿。但是相邻的岛屿会合成一个大岛屿，因此如果直接根据是否为陆地来计数会把相邻的岛屿重复计入。那要怎么办呢？很简单，如果我们发现了一块岛屿，就让这个岛屿从地图上消失就可以了。

那怎么样算消失呢？把这个岛屿上所有的1都变成0即可。这样就不会重复计入相同的岛屿了

1.深度优先沉没魔法

对于把所有相邻的1都变成0，我们可以很自然地想到用递归的方式进行处理。就是深度优先搜素了。只要满足递归条件，我们就进入处理当前位置的陆地以及和他相邻的上下左右四个方向的陆地。

大致步骤是：

①扫描整个数组

②发现1则计数值+1，并使用深度优先沉没魔法

③返回计数值

具体代码如下：

python 复制代码

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        #岛屿沉没术---深度优先施法
        #一旦检查出有1的位置就把它周围的1和它自身也变成0
        n,m = len(grid), len(grid[0])
        
        #沉没术函数
        def dfs(x:int, y:int):
            #沉没终止条件
            if x < 0 or x >= n or y < 0 or y >= m or grid[x][y] == '0':
                return

            #沉没自己以及上下左右的岛屿
            grid[x][y] = '0'
            dfs(x+1, y)
            dfs(x-1, y)
            dfs(x, y-1)
            dfs(x, y+1)

        #检索需要发生沉没的岛屿
        res = 0
        for i in range(n):
            for j in range(m):
                if grid[i][j] == '1':
                    dfs(i, j)
                    res += 1
        
        return res

时间复杂度：O（MN）

空间复杂度：O（MN）【最坏的情况下，整个数组都是1的时候会达到的递归深度】

2.广度优先沉没魔法

当然，我们还可以用广度优先的方式来施展沉没魔法。

①当发现是1的时候，我们就把这个位置的值变为0，并加入队列中。

②从队首弹出元素，并把它上下左右四个方向满足加入条件的位置（没有越界且值为1）加入队列中

③若队列不为0则重复步骤二

具体代码如下:

python 复制代码

import queue

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        #岛屿沉没术---广度优先施法
        #一旦检查出有1的位置就把它周围的1和它自身也变成0
        n,m = len(grid), len(grid[0])
        res = 0
        for i in range(n):
            for j in range(m):
                if grid[i][j] == '1':
                    res += 1
                    #用广度优先法术进行沉没
                    #召唤一个队列法具
                    q = queue.Queue()
                    grid[i][j] = '0'
                    q.put((i,j))
                    #开始施法
                    while not q.empty():
                        #获取队首元素
                        x,y = q.get()
                        #把上下左右合法位置加入队列
                        if x+1 < n and grid[x+1][y] == '1':
                            grid[x+1][y] = '0'
                            q.put((x+1, y))
                        if x-1 >= 0 and grid[x-1][y] == '1':
                            grid[x-1][y] = '0'
                            q.put((x-1, y))
                        if y+1 < m and grid[x][y+1] == '1':
                            grid[x][y+1] = '0'
                            q.put((x, y+1))
                        if y-1 >= 0 and grid[x][y-1] == '1':
                            grid[x][y-1] = '0'
                            q.put((x, y-1))

        return res

时间复杂度：O（NM）

空间复杂度：O（min(M,N)）【最坏的情况是所有点都是陆地的时候】

其他思路：

官方题解还提供了一种叫做并查集的方式来搜索

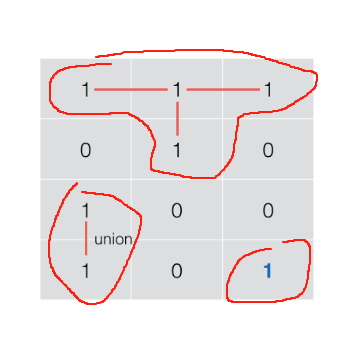
总体的意思是把相邻的陆地节点都连接到一起。

大致的思想步骤如下：

①首先初始化父节点数组parent：把所有为陆地的位置的值存入一维数组的对应位置（比如2X2大小的矩阵，则二维索引（1,1）存入一维数组对应位置是1X2+1 = 3），并记录有几个这样的节点。【这一步的意义是让所有陆地节点的初始根节点为自身】

②尝试合并两个相邻的陆地节点：先用各自的二维索引转化为一维索引值后去父节点数组parent中查找这两个节点对应的根节点rootx,rooty（查找的过程中会顺便根据到达的节点递归地更新的节点的根节点）

如果查找得到的根节点相同，那就说明已经连接在一起，让rootx对应的秩+1【这里是为了尽可能减低树的高度，并默认让rootx一直对应最高的秩】
如果查找得到的根节点不同，那就说明还没有连接在一起，则进行连接操作：先把 rootX设置为秩比较高的那个索引位置，然后把rooty位置的根节点设置为rootX，并让计数值-1【-1是说明孤立的节点减少了一个】

③扫描处理完整个数组之后返回计数值

具体代码如下:

（这里我只是添加了方便理解的注释，代码来源于LeetCode的官方题解：200. 岛屿数量

python 复制代码

class UnionFind:
    def __init__(self, grid):
        m, n = len(grid), len(grid[0])
        self.count = 0
        self.parent = [-1] * (m * n)
        self.rank = [0] * (m * n)
        for i in range(m):
            for j in range(n):
                if grid[i][j] == "1":
                    self.parent[i * n + j] = i * n + j  #所有为1的位置目前都视为孤立的，对应根节点是自己
                    self.count += 1
    
    #用于找到传入索引值处的根节点
    def find(self, i):
        #如果传入的索引值和当前索引位置的值不相同，那就继续递归地查找其根节点
        if self.parent[i] != i:
            self.parent[i] = self.find(self.parent[i])

        #如果传入索引值和当前索引位置的值相同，那就说明它就是根节点了（比如parent[i] == 0   i == 0)
        return self.parent[i]
    
    #用于把两个节点位置合并起来
    def union(self, x, y):
        rootx = self.find(x)
        rooty = self.find(y)
        #不相等的话说明这两个点还没有结合到一起（结合到一起的标志是可以找到同一个根节点）
        if rootx != rooty:
            #如果x比y的秩更低，那就把它们的值进行交换（总是让rootx(更高的秩)作为父节点）
            if self.rank[rootx] < self.rank[rooty]:
                rootx, rooty = rooty, rootx
            #把rooty处的父节点设置为rootx
            self.parent[rooty] = rootx

            #如果它们的秩相等
            if self.rank[rootx] == self.rank[rooty]:
                #那就让x的秩+1
                self.rank[rootx] += 1
            
            #标记当前孤立的节点数-1
            self.count -= 1
    
    def getCount(self):
        return self.count

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        nr = len(grid)
        if nr == 0:
            return 0
        nc = len(grid[0])

        uf = UnionFind(grid)
        num_islands = 0
        for r in range(nr):
            for c in range(nc):
                if grid[r][c] == "1":
                    grid[r][c] = "0"
                    for x, y in [(r - 1, c), (r + 1, c), (r, c - 1), (r, c + 1)]:
                        if 0 <= x < nr and 0 <= y < nc and grid[x][y] == "1":
                            uf.union(r * nc + c, x * nc + y)
        
        return uf.getCount()

时间复杂度：O(MN×α(MN))

空间复杂度：O(MN)

一些个人理解和解释：

①秩是什么：这里的秩应该是指让当前各个节点连接而成的树的最高位置。

比如这两颗树的节点数是一样的，但是它们选择的根节点不同使得树的高度不同（一个是3，一个是4），而秩就是和选择这里面哪一个节点作为树的根节点是有关的。

②Find函数：那个函数初看有点奇怪，奇怪主要是对 parent数组的意义不理解导致的，parent数组的含义应该是每个位置对应的根节点位置，初始的时候默认每个节点的根节点都是自身，因此Find函数主要是用于返回当前节点的父节点。那它干什么要每次还递归地去检索呢？直接返回里面的值不就行了？这是因为它当前指向的根节点不一定是最新的根节点位置。

比如parent[0] == 0 parent[1] == 0 parent[2] == 1

传入查找的位置i == 2，此时parent[2] != 2，

那就只能parent[2] == find(parent[2])

递归传入i == 1，此时parent[1] != 1,

那就只能parent[1] == find(parent[1])

递归传入i == 0，此时parent[0] == 0，所以返回0。此时才把parent[2]更新到最新的根节点位置0。

总结：

①对于要检索处理一片区域的问题，利用深搜或者广搜都是很好的解决方案

②对于要处理连接的问题，可以用并查集的方式来处。它的主要思想是把相邻的节点的根节点都设置为同一个，这样就算标记它们是同一个节点了。