在数据结构的世界里,图是一种比数组、链表、树更为复杂的非线性结构,它能够轻松表示现实生活中多对多的关系,比如社交网络中的好友关系、城市交通路线中的站点连接等。而要高效地存储和操作图,选择合适的存储结构至关重要。今天,我们就来重点探讨图的一种常用存储方式 ------ 邻接链表,以及如何用 C 语言实现它。
一、图的基础认知:为何需要邻接链表?
首先,我们简单回顾一下图的基本概念。图由顶点(Vertex)和边(Edge)两部分组成,根据边是否有方向,可分为有向图和无向图。在存储图时,最直观的两种方式是邻接矩阵和邻接链表。
邻接矩阵通过一个二维数组来存储图的信息,数组的行和列分别代表顶点,数组元素表示对应两个顶点之间是否有边。这种方式虽然查询边的存在性很高效,但当图中的顶点数量多而边数量少(即稀疏图)时,会浪费大量的存储空间。比如一个有 1000 个顶点但只有 10 条边的稀疏图,邻接矩阵需要存储 1000×1000=100 万个元素,其中大部分都是无效值,这显然不够高效。
而邻接链表恰好解决了这个问题。它采用 "顶点数组 + 边链表" 的组合形式,为每个顶点建立一个链表,链表中存储该顶点直接相连的邻接顶点信息。这种结构在稀疏图中能极大节省存储空间,同时遍历某个顶点的所有邻接顶点也十分便捷,因此在实际开发中被广泛应用。
二、邻接链表的结构设计:顶点与边的 "携手"
邻接链表的核心结构由两部分组成:顶点节点(Vertexnode)和边节点(Edgenode),再通过一个图结构(GrphAdjlist)将它们整合起来。
1. 边节点(Edgenode)
边节点主要用于存储邻接顶点的信息,以及指向下一个边节点的指针。其结构体定义如下:
typedef struct Edgenode {
int adx; // 邻接点在顶点数组的下标,标记与当前顶点相连的顶点位置
struct Edgenode *next; // 指向下一个边节点,形成链表结构
} Edgenode;
这里的adx存储的是邻接顶点在顶点数组中的索引,通过它我们能快速找到对应的顶点;next指针则让多个边节点串联起来,形成一个链表,记录当前顶点的所有邻接顶点。
2. 顶点节点(Vertexnode)
顶点节点用于存储顶点自身的信息,以及指向该顶点对应的边链表的头指针。其结构体定义如下:
typedef struct Vertexnode {
int data; // 顶点信息,此处用整数表示顶点编号
Edgenode* firstedge; // 指向第一个边节点,即边链表的表头
} Vertexnode, Adjlist[maxver];
其中data存储顶点的具体信息,比如在城市交通图中可以是城市编号;firstedge是一个指向边节点的指针,它指向当前顶点的边链表的第一个节点,通过这个指针我们可以遍历该顶点的所有邻接顶点。另外,这里还定义了Adjlist[maxver],它本质上是一个顶点节点数组,maxver是宏定义的最大顶点数,用于限制图中顶点的数量。
3. 图结构(GrphAdjlist)
图结构用于整合顶点数组、顶点数和边数,方便对整个图进行管理。其结构体定义如下:
typedef struct GrphAdjlist {
Adjlist adjlist; // 邻接表,即顶点节点数组
int vernum; // 顶点数,记录图中实际的顶点数量
int edgenum; // 边数,记录图中实际的边数量
} GrphAdjlist;
通过这个结构,我们可以清晰地获取图的关键信息,无论是后续创建图、遍历图还是其他操作,都能以此为基础展开。
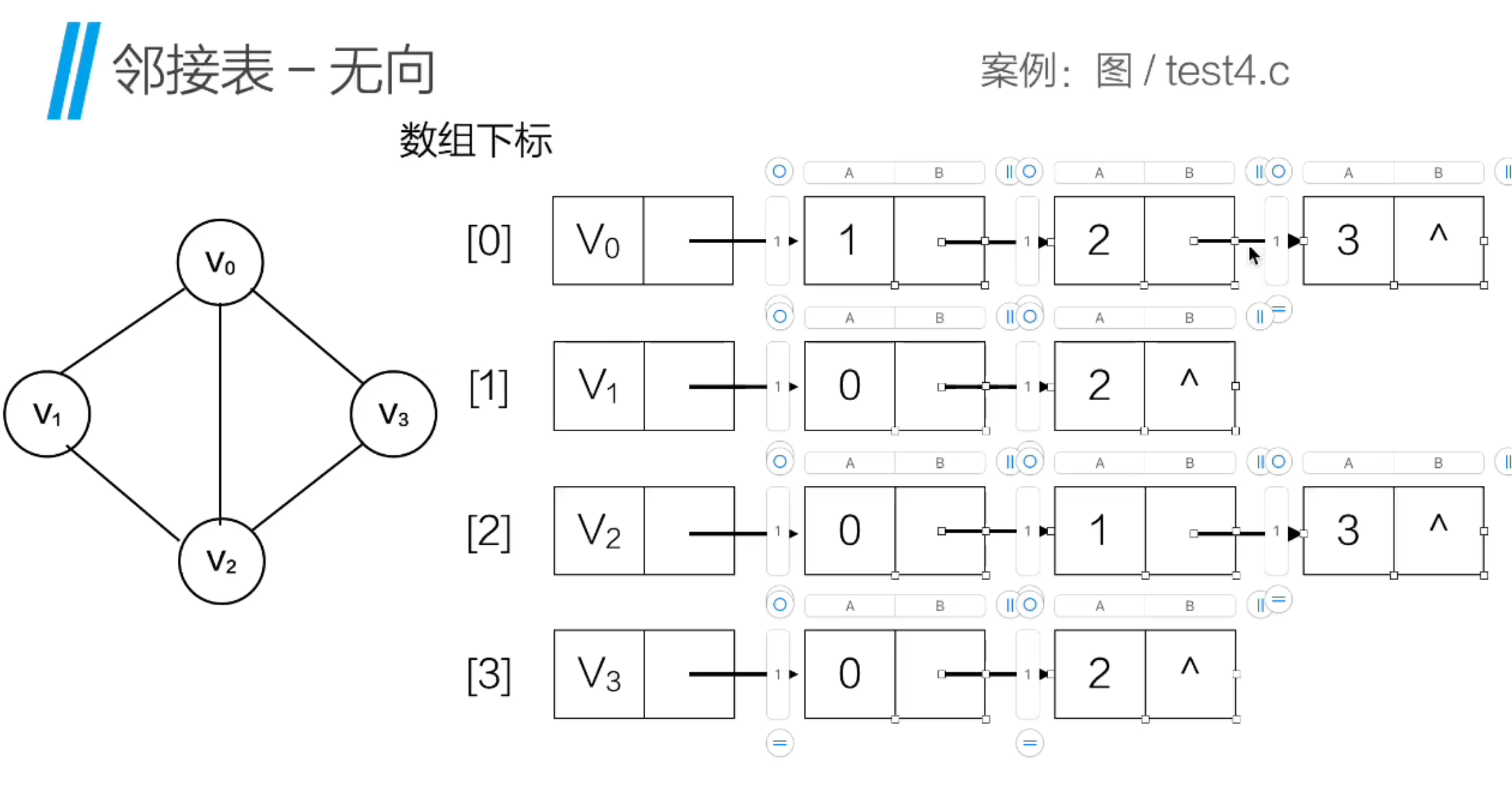
三、邻接链表的创建:一步步构建无向图
了解了邻接链表的结构后,我们就可以着手创建图了。这里以无向图为例,讲解邻接链表的创建过程。无向图的特点是边没有方向,比如顶点 A 和顶点 B 相连,那么在邻接链表中,A 的边链表要包含 B,B 的边链表也要包含 A。
1. 初始化顶点数组
首先,我们需要初始化顶点数组中的每个顶点。将每个顶点的data设置为对应的顶点编号,同时将firstedge初始化为NULL,表示初始状态下每个顶点都没有邻接顶点,边链表为空。代码实现如下:
// 初始化顶点
for (int i = 0; i < G->vernum; i++) {
G->adjlist[i].data = i;
G->adjlist[i].firstedge = NULL;
}
在示例代码中,我们设定图的顶点数vernum为 4,顶点编号分别为 0、1、2、3,通过循环依次完成每个顶点的初始化。
2. 构建边链表(头插法)
接下来,我们需要根据边的信息构建边链表。这里采用头插法的方式插入边节点,头插法的优势是插入效率高,只需修改指针即可完成节点插入。
首先,我们定义一个二维数组edges来存储所有边的信息,每一行的两个元素分别表示一条边的两个顶点。比如edges[5][2] = {{0, 1}, {0, 2}, {0, 3}, {1, 2}, {2, 3}}表示图中有 5 条边,分别连接顶点 0 与 1、0 与 2、0 与 3、1 与 2、2 与 3。
然后,对于每条边,我们需要创建两个边节点(因为是无向图),分别插入到两个顶点的边链表中。具体步骤如下:
- 对于边(from, to),创建第一个边节点e1,将其adx设置为to,然后将e1插入到from顶点的边链表头部(即让e1->next指向from顶点当前的firstedge,再将from顶点的firstedge指向e1)。
- 同样,创建第二个边节点e2,将其adx设置为from,插入到to顶点的边链表头部。
代码实现如下:
// 定义边集合
int edges[5][2] = {``{0, 1}, {0, 2}, {0, 3}, {1, 2}, {2, 3}};
// 构建边表(头插法)
for (int i = 0; i < G->edgenum; i++) {
int from = edges[i][0];
int to = edges[i][1];
// 创建 from->to 的边节点(动态分配内存)
Edgenode* e1 = (Edgenode*)malloc(sizeof(Edgenode));
e1->adx = to;
e1->next = G->adjlist[from].firstedge;
G->adjlist[from].firstedge = e1;
// 创建 to->from 的边节点(无向图双向)
Edgenode* e2 = (Edgenode*)malloc(sizeof(Edgenode));
e2->adx = from;
e2->next = G->adjlist[to].firstedge;
G->adjlist[to].firstedge = e2;
}
通过这样的循环,我们就能逐步构建出整个无向图的邻接链表。
四、邻接链表的输出:直观展示图的结构
创建完邻接链表后,我们需要通过输出函数来直观地查看图的结构,验证邻接链表是否构建正确。输出的思路是遍历每个顶点,然后沿着每个顶点的边链表,依次输出该顶点的所有邻接顶点。
具体实现步骤如下:
- 循环遍历顶点数组中的每个顶点,先输出当前顶点的编号。
- 对于每个顶点,定义一个边节点指针p,初始时让p指向该顶点的firstedge。
- 当p不为NULL时,输出p->adx(即邻接顶点的编号),然后让p指向p->next,继续遍历下一个邻接顶点。
- 当边链表遍历结束(p为NULL),输出一个 "^" 表示该顶点的邻接顶点已全部输出,然后进入下一个顶点的遍历。
代码实现如下:
void printgrph(GrphAdjlist G) {
printf("图的邻接表:\n");
for (int j = 0; j < G.vernum; j++) {
printf("V%d->", G.adjlist[j].data); // 输出当前顶点编号
Edgenode* p = G.adjlist[j].firstedge;
while (p) {
printf("%d->", p->adx); // 输出邻接顶点编号
p = p->next;
}
printf("^\n"); // 表示邻接顶点遍历结束
}
}
在示例代码中,运行输出后,我们会看到类似如下的结果:
图的邻接表:
V0->3->2->1->^
V1->2->0->^
V2->3->1->0->^
V3->2->0->^
这个结果清晰地展示了每个顶点的邻接顶点,比如顶点 0 的邻接顶点是 3、2、1,与我们定义的边集合完全一致,说明邻接链表构建成功。
五、总结:邻接链表的优势与应用场景
通过以上对邻接链表的结构设计、创建和输出的讲解,我们可以总结出邻接链表的几个显著优势:
- 节省存储空间:对于稀疏图,邻接链表只存储实际存在的边,避免了邻接矩阵中大量无效值的存储,极大地节省了内存空间。
- 高效遍历邻接顶点:要遍历某个顶点的所有邻接顶点,只需沿着该顶点的边链表依次访问即可,时间复杂度为 O (边数),效率较高。
- 灵活添加边:采用头插法添加边节点时,只需修改几个指针,操作简单高效。
当然,邻接链表也有一些局限性,比如查询两个顶点之间是否存在边时,需要遍历对应顶点的边链表,时间复杂度相对邻接矩阵较高。但在大多数实际应用场景中,尤其是稀疏图的处理,邻接链表的优势更为突出,因此它被广泛应用于图的深度优先搜索(DFS)、广度优先搜索(BFS)、最短路径算法(如 Dijkstra 算法)等领域。
掌握邻接链表,不仅能帮助我们更好地理解图的存储和操作,也是深入学习图相关算法的基础。希望通过本文的讲解,大家对邻接链表有了更清晰的认识,后续可以尝试在此基础上实现更多图的相关算法,进一步提升自己的数据结构功底。