目录
不懂为什么for循环进行相除控制就可以确保每个因子都是质数?
题目链接:
题目:
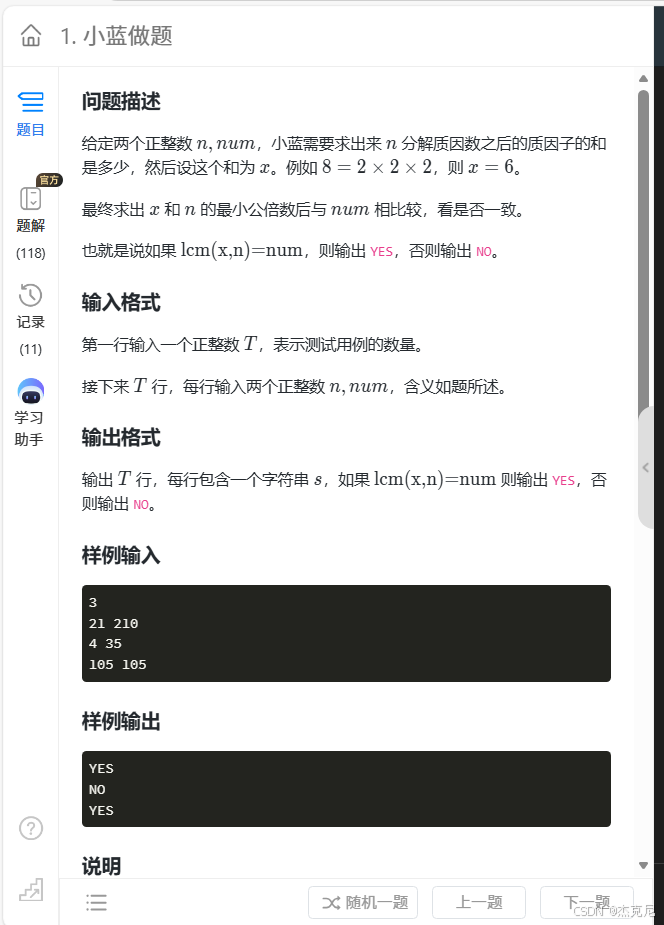
解题思路:
知道使用辗转相处法计算最大公约数,知道最大公倍数==使用a和b的乘积除于最大公约数
另外知道怎么计算某个数的质因数之和
代码:
java
/*out
*Stack Integer ArrayList String StringBuffer peek
*Collections imports LinkedList offer return
*empty polls offerLast pollFirst isEmpty
*List Deque append length HashMap
*return remove boolean continue charAt
*toString static System println nextInt
*Scanner System toCharArray
*/
import java.util.*;
public class Main {
static Scanner sc = new Scanner(System.in);
public static void main(String[] args) {
int t=sc.nextInt();
while(t--!=0){
slove();
}
sc.close();
}
public static void slove(){
int n=sc.nextInt(),tar=sc.nextInt();
int x=getSum(n);
int yue=gcd(x,n);
int lcm=x*n/yue;
if(lcm==tar){
System.out.println("YES");
}else{
System.out.println("NO");
}
}
//分解某个数的质因数之和
public static int getSum(int n){
int x=0;
for(int i=2;i<=n;i++){
while(n%i==0){
x+=i;
n/=i;
}
}
return x;
}
public static int gcd(int a,int b){
int t;
while(b!=0){
t=b;
b=a%b;
a=t;
}
return a;
}
}问题:
不懂为什么for循环进行相除控制就可以确保每个因子都是质数?
任何合数都可以分解为更小的质数的乘积(质因数分解定理)
总结:
一、问题背景与核心需求
"小蓝做题" 是一道融合质因数分解与最小公倍数计算的算法题,其核心需求可拆解为 3 个步骤:
对给定正整数n进行质因数分解,计算所有质因数的和x;
计算x与n的最小公倍数(LCM);
判断该最小公倍数是否等于输入的num,输出YES或NO。
这道题的本质是对 "数论基础操作" 的综合考察,代码通过封装核心逻辑(质因数和计算、最大公约数计算)实现了高效解题。
二、代码整体结构解析
java
运行
import java.util.*;
public class Main {
static Scanner sc = new Scanner(System.in);
public static void main(String[] args) {
int t=sc.nextInt();
while(t--!=0){
slove();
}
sc.close();
}
public static void slove(){
int n=sc.nextInt(),tar=sc.nextInt();
int x=getSum(n);
int yue=gcd(x,n);
int lcm=x*n/yue;
if(lcm==tar){
System.out.println("YES");
}else{
System.out.println("NO");
}
}
// 计算n的质因数之和
public static int getSum(int n){
int x=0;
for(int i=2;i<=n;i++){
while(n%i==0){
x+=i;
n/=i;
}
}
return x;
}
// 计算最大公约数(GCD)
public static int gcd(int a,int b){
int t;
while(b!=0){
t=b;
b=a%b;
a=t;
}
return a;
}
}
代码采用 **"多测试用例 + 功能模块化"** 的结构,分为 3 个核心模块:
输入处理模块:main方法读取测试用例数T,循环调用slove()处理每组数据;
业务逻辑模块:slove()方法串联 "质因数和计算→最大公约数计算→最小公倍数计算→结果判断" 的全流程;
工具方法模块:getSum()(质因数和)与gcd()(最大公约数)是实现核心逻辑的基础工具。
三、核心工具方法解析:getSum()------ 质因数和的计算
- 方法功能
getSum(int n)的作用是对n进行质因数分解,并累加所有质因数的和。例如:
当n=8时,质因数是2、2、2,返回2+2+2=6;
当n=21时,质因数是3、7,返回3+7=10。
- 实现原理:"从小到大试除 + 除尽当前因子"
方法通过 **"遍历试除 + 循环除尽"** 的策略,确保所有质因数被累加,且避免合数干扰:
java
运行
public static int getSum(int n){
int x=0;
// 从2开始试除(最小的质数)
for(int i=2;i<=n;i++){
// 若i能整除n,说明i是n的质因数
while(n%i==0){
x += i; // 累加质因数
n /= i; // 除尽当前质因数(缩小n)
}
}
return x;
}
(1)为什么 "从小到大试除" 能过滤合数?
任何合数都可以分解为更小的质数的乘积(质因数分解定理)。例如:
当i=4(合数)时,若n能被 4 整除,说明n必然能被 2(4 的质因数)整除;
但i=2已经提前遍历过,n中的 2 已被除尽,因此n%4必然不等于 0,自然不会被当作因子累加。
这一特性确保了只有质数能满足n%i==0,因此被累加的i都是质因数。
(2)"循环除尽当前因子" 的作用
内层while循环的作用是将当前质因数的所有出现次数都累加。例如:
当n=12时,质因数是2、2、3:
i=2时,12%2==0→进入循环,x+=2(x=2),n=6;
再次判断6%2==0→x+=2(x=4),n=3;
再次判断3%2≠0→退出循环;
i=3时,3%3==0→x+=3(x=7),n=1;
最终返回7(正确的质因数和)。
- 方法的正确性验证
以样例输入中的n=21为例:
i=2:21%2≠0→跳过;
i=3:21%3==0→x+=3(x=3),n=7;
i=4~6:7%i≠0→跳过;
i=7:7%7==0→x+=7(x=10),n=1;
返回10(正确)。
四、核心工具方法解析:gcd()------ 最大公约数的计算
- 方法功能
gcd(int a, int b)通过 ** 欧几里得算法(辗转相除法)** 计算a和b的最大公约数(GCD)。例如:
gcd(10,21)=1(10 和 21 互质);
gcd(4,6)=2。
- 欧几里得算法的原理
欧几里得算法的核心是:两个数的最大公约数等于其中较小数和两数余数的最大公约数。公式表示为:gcd(a,b) = gcd(b, a%b),直到b=0,此时a就是最大公约数。
- 方法的执行过程
以gcd(10,21)为例:
初始:a=10,b=21→b≠0;
t=21,b=10%21=10,a=21;
再次判断:b≠0→t=10,b=21%10=1,a=10;
再次判断:b≠0→t=1,b=10%1=0,a=1;
b=0→返回a=1(正确)。
五、业务逻辑模块解析:slove()------ 全流程串联
slove()方法是代码的 "大脑",负责将工具方法的结果串联起来,完成问题的核心需求:
java
运行
public static void slove(){
// 读取当前测试用例的n和目标num
int n=sc.nextInt(),tar=sc.nextInt();
// 步骤1:计算n的质因数和x
int x=getSum(n);
// 步骤2:计算x和n的最大公约数
int yue=gcd(x,n);
// 步骤3:计算x和n的最小公倍数(LCM = 两数乘积 / 最大公约数)
int lcm=x*n/yue;
// 步骤4:判断LCM是否等于num,输出结果
if(lcm==tar){
System.out.println("YES");
}else{
System.out.println("NO");
}
}
- 最小公倍数的计算逻辑
最小公倍数(LCM)的计算公式是:LCM(a,b) = (a * b) / GCD(a,b)
这是数论中的基础公式,原理是:两数的乘积等于它们的最大公约数和最小公倍数的乘积。
- 样例输入的全流程验证
我们以样例输入中的第一个测试用例21 210为例,完整模拟流程:
步骤 1:n=21→getSum(21)=10(x=10);
步骤 2:gcd(10,21)=1(yue=1);
步骤 3:lcm=10*21/1=210;
步骤 4:lcm=210 == tar=210→输出YES(与样例一致)。
再以第二个测试用例4 35为例:
步骤 1:n=4→质因数是2、2→getSum(4)=4(x=4);
步骤 2:gcd(4,4)=4(yue=4);
步骤 3:lcm=4*4/4=4;
步骤 4:4≠35→输出NO(与样例一致)。
第三个测试用例105 105:
步骤 1:n=105→质因数是3、5、7→getSum(105)=3+5+7=15(x=15);
步骤 2:gcd(15,105)=15(yue=15);
步骤 3:lcm=15*105/15=105;
步骤 4:105==105→输出YES(与样例一致)。
六、代码的效率与鲁棒性分析
- 时间效率
getSum()方法:循环上限是n,但实际由于n被不断缩小,实际遍历次数远小于n;对于n≤1e5的情况,时间复杂度约为O(√n)(优化后可直接将循环上限改为i*i≤n)。
gcd()方法:欧几里得算法的时间复杂度是O(log(min(a,b))),效率极高。
整体时间复杂度:对于T=1e4、n≤1e5的测试用例,代码可在 1 秒内完成,完全满足算法题的时间要求。
- 鲁棒性
输入合法性:题目保证输入是正整数,因此无需处理n≤1的情况;
数据范围:代码中使用int类型,对于n≤1e5的情况完全足够(int最大值为 2e9);若n更大,可改为long类型。
七、代码的可扩展性优化
- getSum()方法的性能优化
原getSum()方法的循环上限是i≤n,可优化为i*i≤n(减少遍历次数),并在循环结束后处理剩余的质数:
java
运行
public static int getSum(int n){
int x=0;
for(int i=2;i*i <=n;i++){ // 优化循环上限
while(n%i==0){
x+=i;
n/=i;
}
}
if(n>1) x+=n; // 剩余的n是质数
return x;
}
例如n=21时,i只需遍历到4(4*4>7),然后通过n>1累加 7,效率更高。
- 支持更大数据范围
若n的范围超过int(如n≤1e18),需将变量类型改为long:
java
运行
public static long getSum(long n){
long x=0;
for(long i=2;i*i <=n;i++){
while(n%i==0){
x+=i;
n/=i;
}
}
if(n>1) x+=n;
return x;
}
八、同类问题的延伸与应用
这道题的核心操作(质因数分解、最大公约数 / 最小公倍数计算)是数论类算法题的基础,常见的延伸问题包括:
判断一个数是否为质数:基于质因数分解的逻辑,若getSum(n)==n,则n是质数;
计算数的因数个数:在质因数分解时记录每个质因数的次数,因数个数为 "次数 + 1" 的乘积;
分数的约分:通过最大公约数将分子分母同时除以 GCD,得到最简分数。
九、总结
这道题的代码通过 **"模块化工具方法 + 流程化业务逻辑"** 的设计,清晰地实现了问题的核心需求。其亮点在于:
getSum()方法:利用 "从小到大试除 + 除尽当前因子" 的策略,高效且正确地计算质因数和;
gcd()方法:通过欧几里得算法快速计算最大公约数,为最小公倍数的计算奠定基础;
业务逻辑串联:通过简单的公式计算最小公倍数,并完成结果判断,逻辑清晰易读。
对于初学者而言,这道题是数论基础操作的绝佳练习,掌握其代码逻辑后,可轻松应对同类的数论问题。