机器学习--处理数值型数据（一）

创作者mateo2025-12-02 8:59

4.0 简介

在机器学习 pipeline 中，数值型数据预处理是模型训练前的核心环节 ------ 原始数值数据往往存在量纲差异、分布不合理、缺失 / 异常值等问题，直接输入模型会导致训练不稳定、效果偏差甚至完全失效。本章围绕数值型数据的 "特征变换、异常值处理、缺失值处理" 三大核心方向，拆解 11 个关键操作的原理、方法、适用场景与实践细节，帮助实现数据的 "清洁、规范、增强"，为后续模型训练打好基础。

4.1 特征的缩放

特征缩放是消除不同特征 "量纲差异" 的基础操作，核心目标是让所有特征处于相似的数值范围内，避免模型被数值量级大的特征（如 "房屋面积（平方米，取值 100-200）"）主导，而忽略量级小的关键特征（如 "房间数（取值 1-5）"）。

4.1.1 常见方法

  1. Min-Max 归一化（最小 - 最大缩放）

    原理：将特征值映射到 [0, 1] 区间，公式为：

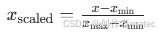
    若需映射到其他区间（如 [-1, 1]），可调整公式为：

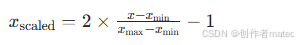
    适用场景：特征分布已知、且需要将数据压缩到固定区间的场景（如神经网络输入、聚类算法）。
    缺点：对异常值敏感（若存在极大 / 极小异常值，会导致大部分数据被压缩到极小范围）。

  2. 绝对最大值缩放(本章节不阐述，主要是阐述常用的)

问题描述

将一个数值型特征值缩放（rescale）到两个特定的值之间。

解决方案

用scikit-learn中的MinmaxScale函数来缩放一个特征数组：

python 复制代码 
import numpy as np
from sklearn import preprocessing

#创建特征
resacle = np.array([[-500.5],[-100.1],[0],[100.1],[900.0]])

#创建缩放器0-1
minmix_scale = preprocessing.MinMaxScaler(feature_range=(0,1))

#缩放特征值
scale_feature = minmix_scale.fit_transform(resacle)

print(scale_feature)

4.1.2 讨论

在机器学习中，缩放是一个很常见的预处理任务。目前所讨论的算法都假设所有的特征在同一取值范围中。最常见的范围是[0,1]，['-1,1].

4.2 特征标准化

标准化（也叫 "Z - 分数标准化"）是将特征转换为均值为 0、标准差为 1的分布，核心目标是让特征符合 "正态分布假设"，适配对数据分布敏感的模型。

4.2.1 原理与公式

对特征 x，计算其均值 (\mu) 和标准差 (\sigma)，转换公式为：

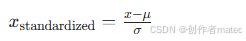
问题描述

对一个特征进行转换，使其平均值为0，标准差为1。

解决方案

scikit-learn的StandardScaler能够同时执行这两个转换。

python 复制代码 
import numpy as np

from sklearn import preprocessing

#创建特征
resacle = np.array([[-100.1],[-200.2],[500.5],[600.6],[9000.9]])

#创建缩放器
minmax_recale = preprocessing.StandardScaler()

#转换特征
standard_recale = minmax_recale.fit_transform(resacle)

print(standard_recale)

标准化方法是机器学习数据与处理中的常用的缩放方法，从经验来看，它比min-max缩放用的更多。如果在主成分析中标准化方法更有用，而在神经网络中更推荐使用min-man缩放。

注意：如果数据中存在很大的异常值，可能会影响特征的平均值和方差，也会对标准化的效果造成不良影响。在这种情况下，使用中位数和四分位数间距进行缩放会更有效。在scikit-learn中，具体的做法就是调用RobustScaler()：

python 复制代码 
import numpy as np

from sklearn import preprocessing

#创建特征
resacle = np.array([[-100.1],[-200.2],[500.5],[600.6],[9000.9]])

#创建缩放器
robust_scale = preprocessing.RobustScaler()

#转换特征
robust_rescale = robust_scale.fit_transform(resacle)
操作 数值范围 对异常值的敏感性 适用模型
Min-Max 归一化 固定区间（如 [0,1]） 高 神经网络、聚类（如 K-Means）
标准化 无固定区间（均值 0） 中（受异常值影响） 线性模型、PCA、SVM

4.3 归一化观察值

此处的 "归一化" 是针对单个样本的特征向量的操作（区别于 4.1 中 "针对特征维度" 的缩放），核心是让单个样本的特征向量满足某种 "归一化约束"，突出样本内部特征的相对占比。

4.3.1 常见方法

  1. L2 范数归一化
    原理：将样本的特征向量除以其 L2 范数（即向量的 "长度"），使转换后的向量 L2 范数为 1，公式为：
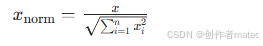
  2. L1 范数归一化
    原理：将样本的特征向量除以其 L1 范数（即向量元素的绝对值之和），使转换后的向量 L1 范数为 1。

4.3.2 适用场景

需衡量 "样本内部特征相对重要性" 的任务（如文本相似度计算：用词频作为特征，归一化后更能体现词的相对占比）；

基于 "距离度量" 的模型（如 KNN、SVM），避免样本因某一特征数值大而主导距离计算。

问题描述

对观察值的每一个特征进行缩放，使其拥有一致的范数（总长度是1）。

解决方案

使用Normallizer并指定norm参数：

python 复制代码 
import numpy as np
from sklearn.preprocessing import Normalizer

#创建特征
norm_rea = np.array([[-100.1],[-200.2],[500.5],[600.6],[9000.9]])

#创建归一化器
norm_reamolizar = preprocessing.Normalizer(norm="l2")

#特征转换矩阵
print(norm_reamolizar.transform(norm_rea))

4.3.3 讨论

很多缩放方法（min-max和标准化方法）都是对特征进行操作的，但其实对观察值也可以进行缩放操作。Normalizer可以对单个观察值进行缩放，使其拥有一致的范数。当一个观察值有多个相同的特征时（例如，做文本分类时，每一个词或每几个词就是一个特征），经常使用这种类型的缩放。

4.4 生成多项式和交互特征

现实中很多问题是非线性的，而线性模型（如线性回归）只能捕捉线性关系 ------ 通过 "生成多项式 / 交互特征"，可以将线性模型扩展为非线性模型，增强对复杂关系的拟合能力。

4.4.1 多项式特征

原理：对单个特征做幂次扩展（如将特征 x 扩展为 (x, x^2, x^3)），捕捉特征自身的非线性趋势。示例：原特征为 (x_1)（房屋面积），扩展为 (x_1, x_1^2)（面积的平方），可捕捉 "面积增大到一定程度后，价格增速放缓" 的非线性关系。

4.4.1 交互特征

原理：将多个特征做 "乘积组合"（如 (x_1 \cdot x_2)），捕捉特征之间的协同影响。

示例：原特征为 (x_1)（房屋面积）、(x_2)（是否学区房，0/1），交互特征 (x_1 \cdot x_2) 可体现 "学区房的面积对价格的影响幅度"。

问题描述

创建多项式特征和交互特征

解决方案

内置的方法：（也可以手动创建多项式特征和交互特征）

python 复制代码 
#加载库
import numpy as np
from sklearn.preprocessing import PolynomialFeatures

#创建特征矩阵
feature = np.array([[2,3],[2,3],[2,3]])

#创建PolynomialFeatures对象
polynomial_feature = PolynomialFeatures(degree=2,include_bias=False)

#polynomial_feature = PolynomialFeatures(degree=2,interaction_only=true,include_bias=False)
#创建多项式特征
x = polynomial_feature.fit_transform(feature)

print(x)

degree参数决定了多项式的最高阶数，degree=2就是创建阶数最高为2的特征。设置interaction_only为true可以创建出来特征只包含交互特征interaction_only=True

4.4.3 讨论

当特征值和目标值之间存在非线性关系时，就需要创建多项式特征。例如年龄可能和身体状况有很大关系，一版年纪越大身体状况就越差，但是他们直接不是线性关系，所以需要对特征x编码----生成这个特征更高阶的形式。

4.5 转换特征

特征转换是通过函数变换调整特征的分布形态，核心目标是：①让特征更接近模型假设的分布（如正态分布）；②增强特征的区分度，提升模型对数据模式的捕捉能力。

4.5.1 常见变换方法

  1. 对数变换
    公式：

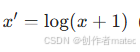
    （+1 是为了避免 (x=0) 时的无定义）。

适用场景：特征呈 "右偏分布"（如收入、用户消费金额 ------ 大部分值较小，少数值极大），可压缩大数值的范围，使分布更接近对称。

  1. 平方根 / 立方根变换

    适用场景：右偏分布特征，但偏态程度弱于对数变换的场景（立方根的压缩幅度比平方根更小）。

  2. Box-Cox 变换

    适用场景：需要自动化优化特征分布的场景，可使特征更接近正态分布，但要求特征值为正。

  3. 反正弦变换

    适用场景：特征是 "比例值"（如通过率、转化率，取值在 [0,1]），可增强比例接近 0 或 1 时的区分度。

问题描述

对一个或者多个特征进行自定义的转换

解决方案

在scikit-learn中，使用FunctionTransformer对一组特征应用一个函数：

python 复制代码 
#加载库
import numpy as np
from sklearn.preprocessing import FunctionTransformer

#创建特征矩阵
transformer = np.array([[2,3],[2,3],[3,4]])

#定义一个简单的函数
def add_ten(x):
    return x + 10

#创建转换器
ten_trandformer = FunctionTransformer(add_ten)

#进行转换
endding = ten_trandformer.transform(transformer)

print(endding)

机器学习数值型数据处理 例题 + 实战代码

数值型数据处理是机器学习预处理的核心环节，涵盖缺失值处理、异常值检测与修正、特征缩放、数据分桶 / 离散化、特征变换 等核心场景。以下结合例题 + 可运行代码，帮你巩固核心知识点。

例题 1：缺失值处理

题目

给定房价数据（单位：万元，取值范围：50~2000），完成：

将房价缩放到 [0,1] 区间；

尝试缩放到 [-1,1] 区间；

分析异常值（如一个 3000 万的极端值）对 Min-Max 的影响。

python 复制代码 
import numpy as np
import pandas as pd
from pandas import DataFrame
from sklearn.preprocessing import MinMaxScaler

# 将房价缩放到 [0,1] 区间；
# 尝试缩放到 [-1,1] 区间；
# 分析异常值（如一个 3000 万的极端值）对 Min-Max 的影响。

# 1. 构造模拟房价数据（含异常值）
house_price = np.array([[80], [150], [300], [500], [800], [1200], [2000], [3000]])  # 3000是异常值
house_price01 = pd.DataFrame(house_price,columns=["price"])
print("原始房价数据（万元）：")
print(house_price)
print(house_price01)

#创建缩放器
min_max_scaler01 = MinMaxScaler(feature_range=(0,1))

#进行特征缩放
scaler01 = min_max_scaler01.fit_transform(house_price)
print("=====缩放到0-1=====")
print(scaler01)
print(f"缩放参数： min = {min_max_scaler01.data_min_[0]},max = {min_max_scaler01.data_max_[0]}")

print("=====缩放到-1-1=====")
#创建缩放器
min_max_scaler02 = MinMaxScaler(feature_range=(-1,1))

#进行特征缩放
scaler02 = min_max_scaler02.fit_transform(house_price)
print("=====缩放到-1-1=====")
print(scaler02)
print(f"缩放参数： min = {min_max_scaler02.data_min_[0]},max = {min_max_scaler02.data_max_[0]}")

#筛选异常数据
house_price01 = house_price01[house_price01['price'] < 2500]
print(house_price01)

scaler_normal = MinMaxScaler(feature_range=(0, 1))
price_normal = scaler_normal.fit_transform(house_price01)
print("\n=== 移除异常值后缩放到 [0,1] ===")
print(price_normal)
print(f"无异常值缩放参数：min={scaler_normal.data_min_[0]}, max={scaler_normal.data_max_[0]}")


# 分析异常值影响
print("\n【异常值影响分析】：")
print(f"含异常值时，800万房价缩放后：{scaler01[4][0]:.4f}")
print(f"无异常值时，800万房价缩放后：{price_normal[4][0]:.4f}")
print("结论：异常值会压缩正常数据的缩放范围，导致正常数据差异被弱化")

例题 2：标准化 + 鲁棒缩放（对比异常值抗性）

题目

给定用户月消费数据（含极端异常值），完成：

用 StandardScaler 做标准化，观察异常值对均值 / 标准差的影响；

用 RobustScaler 做鲁棒缩放，对比结果；

计算两种缩放后数据的均值 / 标准差，验证鲁棒性。

python 复制代码 
import numpy as np
import pandas as pd
from sklearn.preprocessing  import StandardScaler,RobustScaler

# 1. 构造消费数据（正常范围：100~500，异常值：5000、-100）
consume01 = np.array([[150], [200], [300], [400], [500], [5000], [-100]])
consume02 = pd.DataFrame(consume01,columns=(["price"]))
print("原始消费数据（元）：")
print(consume01)
print(consume02)


#去除异常值
consume03 = consume02[(consume02["price"]>=100 ) & (consume02["price"]<=500) ]
print(consume03)


# 用 StandardScaler 做标准化，观察异常值对均值 / 标准差的影响；
#创建缩放器
standar_sc = StandardScaler()

#标准化缩放数据
print("====数据清理后====")
standar_res1 = standar_sc.fit_transform(consume03)
print(standar_res1)
print(f"原始数据均值mean= {standar_sc.mean_[0]:.2f}")
print(f"原始数据标准差std= {standar_sc.scale_[0]:.2f}")
print(f"标准化均值mean: = {standar_res1.mean():.6f}")
print(f"标准化标准差： = {standar_res1.std():.6f}")
print("====数据清理前====")
standar_res2 = standar_sc.fit_transform(consume02)
print(standar_res2)

#用 RobustScaler 做鲁棒缩放，对比结果；
print("=====RobustScaler 做鲁棒缩放=====")
robutst_sca = RobustScaler()
robutst_res = robutst_sca.fit_transform(consume03)
print(robutst_res)
相关推荐
roman_日积跬步-终至千里1 小时前
【模式识别与机器学习（6）】主要算法与技术（下篇：高级模型与集成方法）之进化计算（Evolutionary Computation）
人工智能·算法·机器学习
禁默1 小时前
机器学习基础入门（第七篇）：神经网络训练优化与常见问题解析
人工智能·神经网络·机器学习
二哈喇子！1 小时前
昇腾平台 vLLM 部署与性能优化实战：高吞吐推理落地指南
人工智能·性能优化
小狗照亮每一天1 小时前
【菜狗学深度学习】注意力机制手撕——20251201
人工智能·深度学习·机器学习
AI视觉网奇1 小时前
数字人 语音驱动
人工智能·python
宁大小白1 小时前
pythonstudy Day24
人工智能·机器学习
胡乱儿起个名1 小时前
Embedding查表操作
python·机器学习·embedding
伯远医学1 小时前
CUT&RUN
java·服务器·网络·人工智能·python·算法·eclipse
攻城狮7号1 小时前
微软开源的Fara-7B 如何让你的电脑长出“双手”
人工智能·fara-7b·微软开源小型语言模型·端侧ai·ai控制电脑
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04BongoCat - 跨平台键盘猫动画工具05Linux下V2Ray安装配置指南06本地部署阿里最新开源的Z-Image07【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连0846个Nano-banana 精选提示词，持续更新中09Labelme从安装到标注：零基础完整指南10Gemini 3.0 Pro Preview 实测报告