引言
前序学习进程中,已经掌握卷积计算的基本原理,但在这里使用了相对简单的卷积核,所以有必要进一步探索,如果卷积核复杂一些,通道数也复杂一些,该如何计算。
原始矩阵
原始矩阵代表了即将被用于卷积计算的原始数据,图像一般使用三个通道表达,因此定义一个三通道矩阵就可以满足要求,这里给出一个简单的定义:
python
# 1. 定义原始输入(3通道5×5)和卷积核1(边缘检测核)
input_tensor = torch.tensor([
# 输入通道1(R):5×5
[
[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10],
[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25]
],
# 输入通道2(G):5×5
[
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35],
[36, 37, 38, 39, 40],
[41, 42, 43, 44, 45],
[46, 47, 48, 49, 50]
],
# 输入通道3(B):5×5
[
[51, 52, 53, 54, 55],
[56, 57, 58, 59, 60],
[61, 62, 63, 64, 65],
[66, 67, 68, 69, 70],
[71, 72, 73, 74, 75]
]
], dtype=torch.float32) # 形状:(3,5,5)这是一个三通道的原始矩阵,每个通道搞内部都是5行5列的图像数据。
卷积核
这里定义了一个相对多维度的卷积核:
python
# 卷积核1(边缘检测核):3个子核,每个3×3
kernel1 = torch.tensor([
[[1, 0, -1], [1, 0, -1], [1, 0, -1]], # 子核1(R通道)
[[1, 0, -1], [1, 0, -1], [1, 0, -1]], # 子核2(G通道)
[[1, 0, -1], [1, 0, -1], [1, 0, -1]] # 子核3(B通道)
], dtype=torch.float32) # 形状:(3,3,3)
# 输出卷积核的大小
kernel1_channels,kernel1_h,kernel1_w=kernel1.shape
print('kernel1_channels=',kernel1_channels)
print('kernel1_h=',kernel1_h)
print('kernel1_w=',kernel1_w)这个多维度的卷积核,从宏观的角度看,可以把每一行看成一个元素即子卷积核。在正式的卷积运算中,卷积核的每一个行组成的子卷积核会分别和构成图像的三个通道进行点积运算。
卷积核会和每个通道内的数据开展运算,所以必须满足子核数量=通道数,当输入的待计算通道数很多时,卷积核也要相应扩充。
卷积计算
卷积计算相对简单,按照每一个子卷积核对应一个通道的规则,在通道内部逐步滑移完成计算即可,这里给出了前两步的计算效果:
python
# 2. 计算(0,0)位置的像素值(左上方3×3区域)
print("=== (0,0)位置计算(左上方3×3)===")
# 直接通过索引范围提取3×3区域(行0-2,列0-2)
input_r_00 = input_tensor[0, 0:kernel1_h, 0:kernel1_w] # R通道:行0-2,列0-2
input_g_00 = input_tensor[1, 0:kernel1_h, 0:kernel1_w] # G通道:行0-2,列0-2
input_b_00 = input_tensor[2, 0:kernel1_h, 0:kernel1_w] # B通道:行0-2,列0-2
r_00 = (input_r_00 * kernel1[0]).sum()
g_00 = (input_g_00 * kernel1[1]).sum()
b_00 = (input_b_00 * kernel1[2]).sum()
pixel_00 = r_00 + g_00 + b_00
print(f"R通道结果:{r_00.item():.0f} | G通道结果:{g_00.item():.0f} | B通道结果:{b_00.item():.0f}")
print(f"(0,0)像素最终值:{pixel_00.item():.0f}\n")
# 3. 计算(0,1)位置的像素值(卷积核右移1步)
print("=== (0,1)位置计算(右移1步的3×3)===")
# 直接通过索引范围提取右移后的3×3区域(行0-2,列1-3)
input_r_01 = input_tensor[0, 0:kernel1_h, 1:1+kernel1_w] # R通道:行0-2,列1-3
input_g_01 = input_tensor[1, 0:kernel1_h, 1:1+kernel1_w] # G通道:行0-2,列1-3
input_b_01 = input_tensor[2, 0:kernel1_h, 1:1+kernel1_w] # B通道:行0-2,列1-3
r_01 = (input_r_01 * kernel1[0]).sum()
g_01 = (input_g_01 * kernel1[1]).sum()
b_01 = (input_b_01 * kernel1[2]).sum()
pixel_01 = r_01 + g_01 + b_01
print(f"R通道结果:{r_01.item():.0f} | G通道结果:{g_01.item():.0f} | B通道结果:{b_01.item():.0f}")
print(f"(0,1)像素最终值:{pixel_01.item():.0f}")完整代码
要想顺利完成计算,应当调用torch模块,此时的完整代码为:
python
# 引入模块
import torch
# 1. 定义原始输入(3通道5×5)和卷积核1(边缘检测核)
input_tensor = torch.tensor([
# 输入通道1(R):5×5
[
[1, 2, 3, 4, 5],
[6, 7, 8, 9, 10],
[11, 12, 13, 14, 15],
[16, 17, 18, 19, 20],
[21, 22, 23, 24, 25]
],
# 输入通道2(G):5×5
[
[26, 27, 28, 29, 30],
[31, 32, 33, 34, 35],
[36, 37, 38, 39, 40],
[41, 42, 43, 44, 45],
[46, 47, 48, 49, 50]
],
# 输入通道3(B):5×5
[
[51, 52, 53, 54, 55],
[56, 57, 58, 59, 60],
[61, 62, 63, 64, 65],
[66, 67, 68, 69, 70],
[71, 72, 73, 74, 75]
]
], dtype=torch.float32) # 形状:(3,5,5)
# 卷积核1(边缘检测核):3个子核,每个3×3
kernel1 = torch.tensor([
[[1, 0, -1], [1, 0, -1], [1, 0, -1]], # 子核1(R通道)
[[1, 0, -1], [1, 0, -1], [1, 0, -1]], # 子核2(G通道)
[[1, 0, -1], [1, 0, -1], [1, 0, -1]] # 子核3(B通道)
], dtype=torch.float32) # 形状:(3,3,3)
# 输出卷积核的大小
kernel1_channels,kernel1_h,kernel1_w=kernel1.shape
print('kernel1_channels=',kernel1_channels)
print('kernel1_h=',kernel1_h)
print('kernel1_w=',kernel1_w)
# 2. 计算(0,0)位置的像素值(左上方3×3区域)
print("=== (0,0)位置计算(左上方3×3)===")
# 直接通过索引范围提取3×3区域(行0-2,列0-2)
input_r_00 = input_tensor[0, 0:kernel1_h, 0:kernel1_w] # R通道:行0-2,列0-2
input_g_00 = input_tensor[1, 0:kernel1_h, 0:kernel1_w] # G通道:行0-2,列0-2
input_b_00 = input_tensor[2, 0:kernel1_h, 0:kernel1_w] # B通道:行0-2,列0-2
r_00 = (input_r_00 * kernel1[0]).sum()
g_00 = (input_g_00 * kernel1[1]).sum()
b_00 = (input_b_00 * kernel1[2]).sum()
pixel_00 = r_00 + g_00 + b_00
print(f"R通道结果:{r_00.item():.0f} | G通道结果:{g_00.item():.0f} | B通道结果:{b_00.item():.0f}")
print(f"(0,0)像素最终值:{pixel_00.item():.0f}\n")
# 3. 计算(0,1)位置的像素值(卷积核右移1步)
print("=== (0,1)位置计算(右移1步的3×3)===")
# 直接通过索引范围提取右移后的3×3区域(行0-2,列1-3)
input_r_01 = input_tensor[0, 0:kernel1_h, 1:1+kernel1_w] # R通道:行0-2,列1-3
input_g_01 = input_tensor[1, 0:kernel1_h, 1:1+kernel1_w] # G通道:行0-2,列1-3
input_b_01 = input_tensor[2, 0:kernel1_h, 1:1+kernel1_w] # B通道:行0-2,列1-3
r_01 = (input_r_01 * kernel1[0]).sum()
g_01 = (input_g_01 * kernel1[1]).sum()
b_01 = (input_b_01 * kernel1[2]).sum()
pixel_01 = r_01 + g_01 + b_01
print(f"R通道结果:{r_01.item():.0f} | G通道结果:{g_01.item():.0f} | B通道结果:{b_01.item():.0f}")
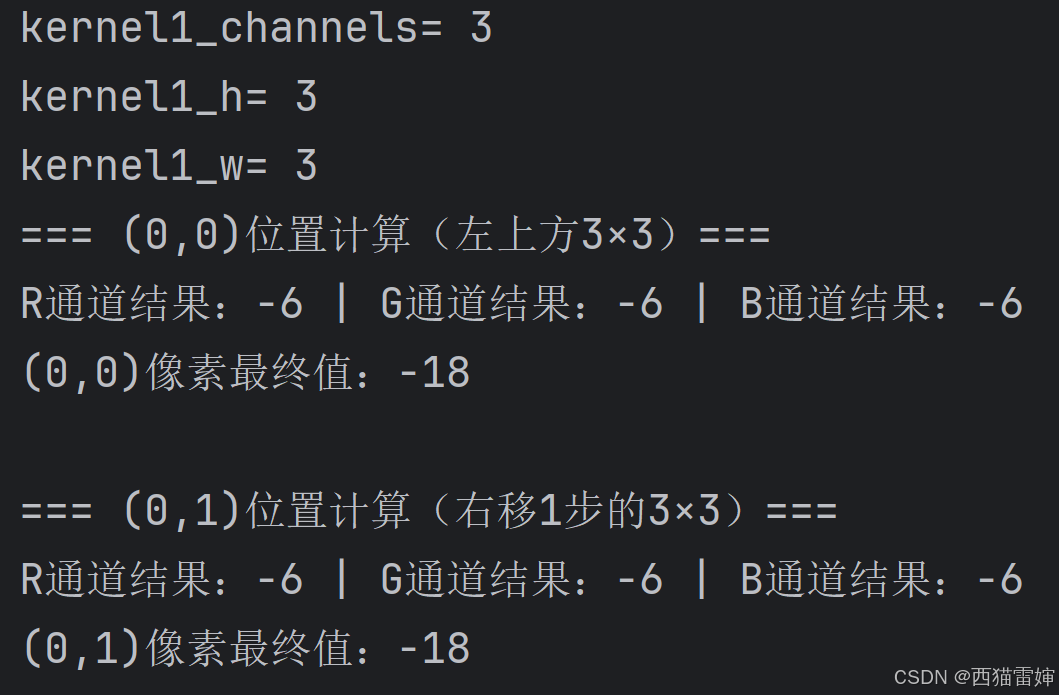
print(f"(0,1)像素最终值:{pixel_01.item():.0f}")代码运行效果
代码运行效果为:
总结
初步学习了多通道数据的卷积运算规则。