Transformer 原理系列（第一章）—— 从序列相关性出发，理解注意力机制的本质

[Transformer 原理系列（第一章）------ 从序列相关性出发，理解注意力机制的本质](#Transformer 原理系列（第一章）—— 从序列相关性出发，理解注意力机制的本质)

[1. 序列数据的本质：样本按时间排列 & 样本之间存在依赖关系](#1. 序列数据的本质：样本按时间排列 & 样本之间存在依赖关系)

[2. 序列模型三大家族：它们都在做"加权求和"](#2. 序列模型三大家族：它们都在做“加权求和”)

[2.1 ARIMA 家族：线性加权](#2.1 ARIMA 家族：线性加权)

[2.2 RNN / LSTM：隐状态传递，本质仍然是加权](#2.2 RNN / LSTM：隐状态传递，本质仍然是加权)

[2.3 CNN 处理序列：局部加权卷积](#2.3 CNN 处理序列：局部加权卷积)

[3. 序列学习的终极问题：如何建立任意两个样本之间的关系？](#3. 序列学习的终极问题：如何建立任意两个样本之间的关系？)

[4. 注意力机制：为每个样本赋予权重，告诉模型"什么更重要"](#4. 注意力机制：为每个样本赋予权重，告诉模型“什么更重要”)

为什么要判断"重要性"？

[5. 样本重要性如何判断？------通过向量相似度](#5. 样本重要性如何判断？——通过向量相似度)

[6. 自注意力（Self-Attention）：让序列中每个样本与所有样本相关](#6. 自注意力（Self-Attention）：让序列中每个样本与所有样本相关)

[7. 从相关性矩阵到 Transformer 的 Q、K、V](#7. 从相关性矩阵到 Transformer 的 Q、K、V)

[8. 总结：为什么注意力机制是序列模型的终极方案？](#8. 总结：为什么注意力机制是序列模型的终极方案？)

[结语：下一章我们将从"注意力公式"正式进入 Transformer 内核](#结语：下一章我们将从“注意力公式”正式进入 Transformer 内核)

Transformer 原理系列（第一章）------ 从序列相关性出发，理解注意力机制的本质

在正式进入 Transformer 的世界之前，我们必须先回答一个根本问题：

序列模型到底在学什么？它们是如何理解"序列中样本与样本之间的关系"的？

无论是自然语言、语音信号、视频帧序列，还是股票价格、传感器连续数据，它们本质上都是序列数据（Sequence Data） 。
序列模型的使命，就是建立序列中不同位置样本之间的相关性。

换句话说：

所有序列任务的核心问题：如何找出样本（token）和样本之间的关系？

这篇文章将带你从传统序列方法讲到注意力机制，最终导向 Transformer 的核心思想。
做好准备，我们要开启这个系列最关键的第一步。

1. 序列数据的本质：样本按时间排列 & 样本之间存在依赖关系

什么是序列数据？

每个样本对应一个时间点（或顺序位置）
样本之间存在前后依赖
目标是理解序列中的"模式"，并据此进行预测、分类、生成等任务

举几个例子：

数据类型	每个样本代表什么	样本之间的联系
文本	一个 token（字 / 词）	句子语义来自 token 之间的关系
股票价格	一个时间点的价格	价格受过去行情影响
语音信号	某一帧幅度	声音需要前后帧一起理解

因此，序列模型面临的最核心工作是：

如何让模型学到序列中任意两个样本之间的重要性？

传统方法和深度学习方法都在解决这个问题。

2. 序列模型三大家族：它们都在做"加权求和"

所有序列任务，说白了都是：

把过去的样本以不同的权重加起来，得到对现在样本的理解。

这种"权重 + 加权求和"的思想贯穿了所有序列模型。

2.1 ARIMA 家族：线性加权

写成公式就是经典 AR：

每个过去样本 ( ) 都乘了一个权重。

2.2 RNN / LSTM：隐状态传递，本质仍然是加权

RNN：

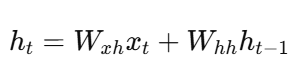
LSTM：

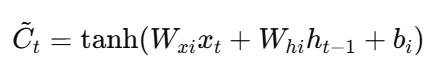
这些模型都把过去样本编码成隐状态 h / C，再加权传递给下一时刻。

只是：

RNN/LSTM 权重固定
序列越长，传播越困难（梯度消失）

2.3 CNN 处理序列：局部加权卷积

本质也是：

卷积核里的 w，对局部样本进行加权求和

只是局部窗口固定，无法捕捉长距离依赖。

3. 序列学习的终极问题：如何建立任意两个样本之间的关系？

把前面总结一下：

ARIMA：只看固定窗口
RNN：依赖隐状态，难看长距离
CNN：只看局部邻居

但是：

序列模型最终需要一个"可以让任意两个样本直接建立联系"的机制。

这才是后续 Transformer 诞生的背景。

所以，注意力机制出现了。

4. 注意力机制：为每个样本赋予权重，告诉模型"什么更重要"

注意力机制（Attention）核心思想一句话：

对一个样本，判断其他样本对它的重要程度，并据此加权求和。

这是一种动态权重机制。

不同于 CNN/RNN 的固定权重，
Attention 的权重来自：

样本之间的语义相关性
位置无关，可以看全局
每次输入都能变化

因此，它特别适合自然语言理解。

为什么要判断"重要性"？

因为序列中不同样本对预测任务的贡献不同。

例子：

尽管今天下了雨 ，但我因为拿到了梦想以求的工作 offer而感到非常开心。

在这个句子里：

"下雨" 对情感分析的贡献不大
"工作 offer" 对情感分析 决定性

注意力机制要做的，就是：

自动找出这些"关键的样本"，并赋予它们更高的权重。

5. 样本重要性如何判断？------通过向量相似度

NLP 模型如何判断两个样本是否相关？

答案是：

计算两个样本（token）的向量之间的相似度。

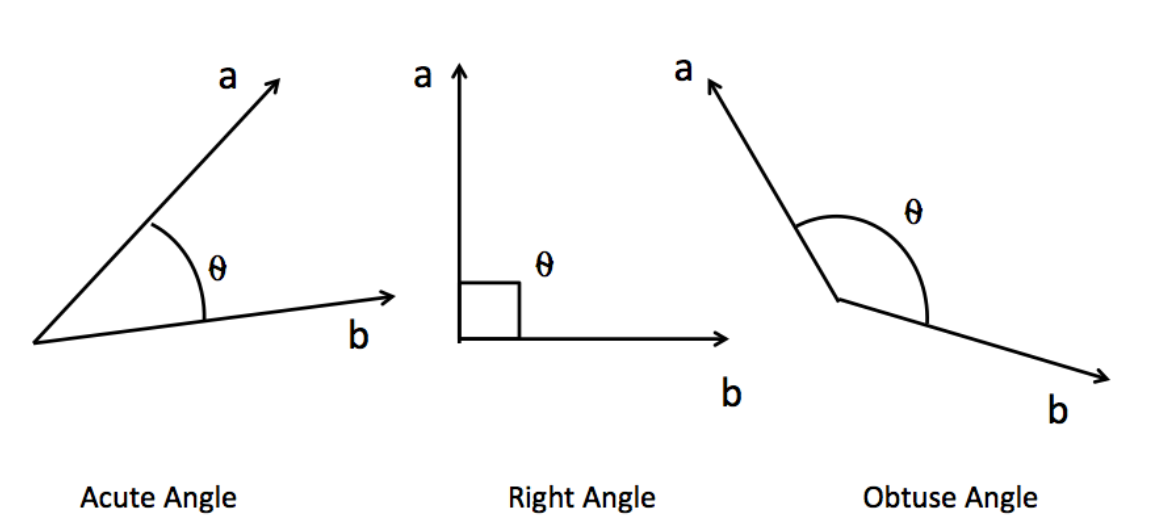
相似度可以通过点积衡量：

方向相近 → 点积大 → 强相关
垂直 → 点积 0 → 无相关
方向相反 → 负值 → 语义相反

下面用图来理解：

公式上：

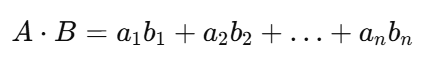
在 NLP 中，向量代表词的语义特征，因此：

"猫" 和 "猫咪" 点积大
"猫" 和 "股票" 点积接近 0

6. 自注意力（Self-Attention）：让序列中每个样本与所有样本相关

假设序列里有两个样本 A、B，它们被编码成向量矩阵 X：

我们通过矩阵乘法得到相似度矩阵：

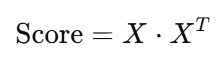
视觉化如下：

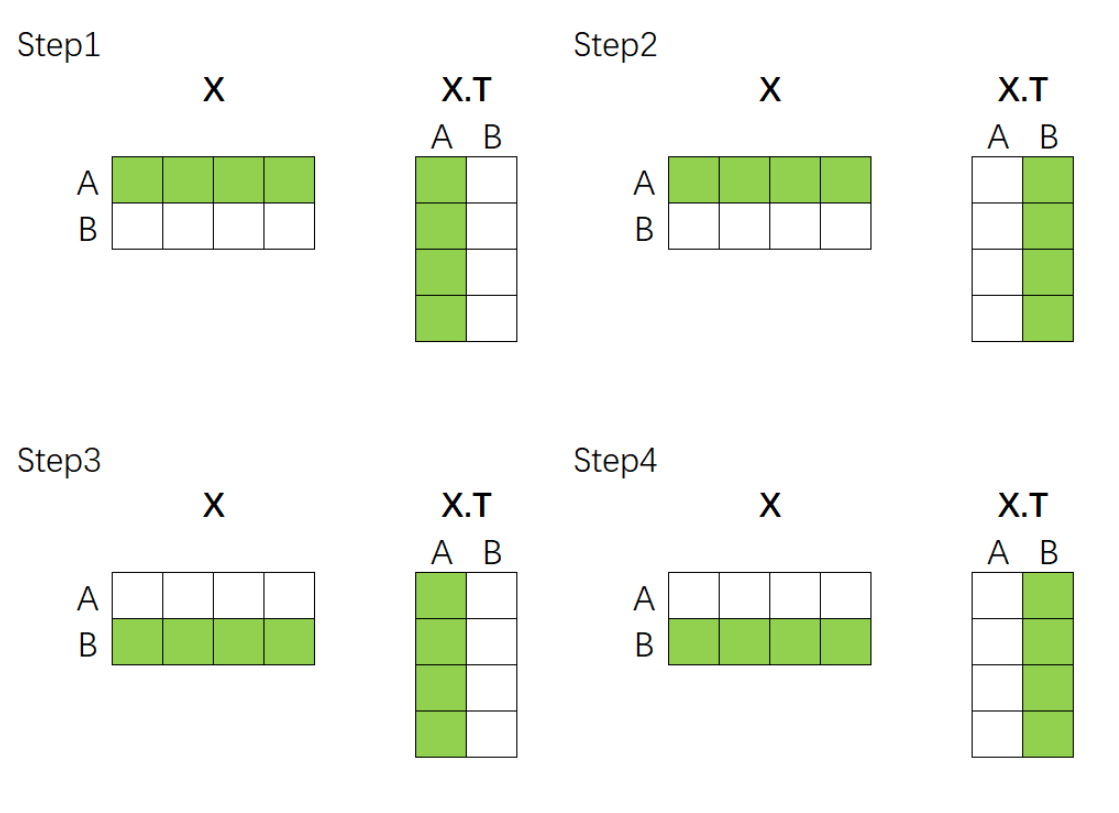
含义非常清晰：

r_AB：样本 A 与样本 B 的相关性
r_BA：样本 B 与样本 A 的相关性
r_AA、r_BB：与自身的相关性

当序列有 n 个 token，就能得到 n × n 的相关性矩阵。

它告诉我们：在这个序列里，每个 token 应该关注哪些 token。

这就是自注意力矩阵的雏形。

7. 从相关性矩阵到 Transformer 的 Q、K、V

真正的 Transformer 不直接用 X 和 X^T，而是引入三组可学习矩阵：

Query（查询）
Key（键）
Value（值）

它们都是通过线性层（矩阵乘法）得到的：

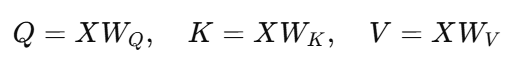
这样：

Q × K^T 得到 相关性矩阵 Score
Score 再经过 Softmax 得到 权重矩阵 Attention
Attention × V 得到 加权求和的结果

整个过程就是：

Q 负责问：我想了解什么？
K 负责答：我能提供什么？
V 负责提供内容：我的信息是什么？

Transformer 的核心，就是这个权重矩阵的计算方式。

8. 总结：为什么注意力机制是序列模型的终极方案？

因为它解决了所有旧模型的痛点：

模型	能否看长距离依赖？	能否动态调整权重？	能否并行？
RNN	困难（梯度消失）	不行	不行
LSTM	比 RNN 好	不行	不行
CNN	局部性强	不行	可以
Transformer	可以看全局	可以	可以

Self-Attention 让模型：

一步建立所有 token 的关系
权重随语境动态变化
并行加速，适配大规模训练
对长序列理解能力极强

因此注意力机制成为现代 NLP 乃至多模态任务的基础。

结语：下一章我们将从"注意力公式"正式进入 Transformer 内核

本章我们完成了 Transformer 的地基建设：

序列数据的本质
序列模型都在做加权求和
注意力如何从相似度出发
自注意力如何构建 token-token 关系
Transformer 引入 Q/K/V 的意义

下一章，我们将深入最关键的公式：

Scaled Dot-Product Attention：
如何从 QKᵀ → Softmax → V，构成最强序列建模组件？