MATLAB物理仿真＜1＞电磁场有限元仿真

一、前言

在我们学习电磁场理论的时候，可能会觉得电磁场仿真听起来就像是那些穿着白大褂的科学家在超级计算机前做的事情，离我们很远。但事实上，借助MATLAB这个强大的工具，我们每个人都可以在自己的电脑上实现电磁场的仿真。

今天，我将带你一步步实现一个二维静电场的有限元仿真，无需深厚的电磁场理论背景，只需一点好奇心和对编程的兴趣。

1.问题的描述

想象一下，我们有一个正方形的区域，比如一块正方形的金属板，我们在中心区域加上一些电荷，然后想知道整个区域内的电势和电场分布。这就是我们今天要解决的问题。具体来说，我们要解决的是二维静电场问题，可以用泊松方程来描述。

2.有限元方法简介

有限元方法是一种数值技术，用来求解偏微分方程。它的基本思想是把一个复杂的区域分割成许多简单的小区域，比如三角形，这些小区域称为"单元"。然后，我们在每个单元内用简单的函数，比如线性函数，使用它们来近似求解，最后把所有的单元组合起来，得到整个区域的解。这就好比把一个城堡分成许多小块，每一块都容易处理，然后拼起来就得到了整个城堡。

二、各个函数的代码

1. 网格生成函数

首先，我们需要将正方形区域划分成许多三角形单元。这就像把一块正方形的地板铺上三角形的地砖。我们使用以下代码生成网格。

Matlab 复制代码

function [nodes, elements] = generate_mesh(L, nx, ny)
%GENERATE_MESH 生成二维矩形区域的三角形网格
%   L: 区域边长
%   nx, ny: x和y方向的节点数
%   返回: 
%     nodes: 节点坐标矩阵 (n×2)
%     elements: 单元连接矩阵 (m×3)

% 创建节点坐标
x = linspace(0, L, nx);
y = linspace(0, L, ny);
[X, Y] = meshgrid(x, y);
nodes = [X(:), Y(:)];

% 创建三角形单元
elements = [];
for i = 1:ny-1
    for j = 1:nx-1
        % 当前单元的四个节点
        n1 = (i-1)*nx + j;
        n2 = (i-1)*nx + j + 1;
        n3 = i*nx + j;
        n4 = i*nx + j + 1;
        
        % 将四边形分成两个三角形
        elements = [elements; n1, n2, n3];
        elements = [elements; n2, n4, n3];
    end
end
end

2. 电荷密度设置函数

接下来，我们设置电荷密度分布。在这个例子中，我们假设中心区域有一个正电荷分布，周围区域电荷密度为零。

Matlab 复制代码

function rho = set_charge_density(nodes, L)
%SET_CHARGE_DENSITY 设置电荷密度分布
%   中心区域有正电荷，边缘区域为零

n = size(nodes, 1);
rho = zeros(n, 1);
center = [L/2, L/2];

for i = 1:n
    % 计算到中心的距离
    dist = norm(nodes(i,:) - center);
    
    % 中心区域设置正电荷
    if dist < L/4
        rho(i) = 1e-9;  % 1 nC/m²
    elseif dist < L/3
        rho(i) = 0.5e-9;  % 0.5 nC/m²
    else
        rho(i) = 0;
    end
end
end

3. 系统组装函数

然后，我们需要组装刚度矩阵和载荷向量。这是有限元方法的核心步骤，我们将每个小三角形的贡献组合起来，形成一个大的线性方程组。

Matlab 复制代码

function [K, F] = assemble_system(nodes, elements, epsilon, rho)
%ASSEMBLE_SYSTEM 组装刚度矩阵和载荷向量
%   返回全局刚度矩阵K和载荷向量F

n_nodes = size(nodes, 1);
n_elements = size(elements, 1);

% 初始化全局矩阵
K = sparse(n_nodes, n_nodes);
F = zeros(n_nodes, 1);

% 对每个单元进行循环
for e = 1:n_elements
    % 获取单元节点
    node_indices = elements(e, :);
    element_nodes = nodes(node_indices, :);
    
    % 计算单元刚度矩阵和载荷向量
    [Ke, Fe] = compute_element_matrices(element_nodes, epsilon, rho(node_indices));
    
    % 组装到全局矩阵 - 修正索引问题
    for i = 1:3
        for j = 1:3
            K(node_indices(i), node_indices(j)) = K(node_indices(i), node_indices(j)) + Ke(i, j);
        end
        F(node_indices(i)) = F(node_indices(i)) + Fe(i);
    end
end
end

function [Ke, Fe] = compute_element_matrices(nodes, epsilon, rho)
%COMPUTE_ELEMENT_MATRICES 计算三角形单元的刚度矩阵和载荷向量

% 三角形面积
x = nodes(:, 1);
y = nodes(:, 2);
area = abs((x(2)-x(1))*(y(3)-y(1)) - (x(3)-x(1))*(y(2)-y(1))) / 2;

% 修正：使用正确的形状函数导数计算
% 对于线性三角形单元，形状函数导数为常数
b = zeros(3, 1);
c = zeros(3, 1);

% 计算b和c系数
b(1) = y(2) - y(3);
b(2) = y(3) - y(1);
b(3) = y(1) - y(2);

c(1) = x(3) - x(2);
c(2) = x(1) - x(3);
c(3) = x(2) - x(1);

% B矩阵 (2×3)
B = [b(1), b(2), b(3);
     c(1), c(2), c(3)] / (2 * area);

% 单元刚度矩阵
Ke = (epsilon * area) * (B' * B);

% 单元载荷向量（假设rho在单元内为常数）
rho_avg = mean(rho);
Fe = (rho_avg * area / 3) * ones(3, 1);
end

4. 边界条件应用函数

我们假设正方形的边界上电势为零（接地），这就是狄利克雷边界条件。我们需要修改刚度矩阵和载荷向量来强加这个条件。

Matlab 复制代码

function [K_mod, F_mod] = apply_boundary_conditions(nodes, K, F, L)
%APPLY_BOUNDARY_CONDITIONS 应用狄利克雷边界条件
%   边界设置为零电势

n_nodes = size(nodes, 1);
tol = 1e-10;

% 找出边界节点
boundary_nodes = [];
for i = 1:n_nodes
    x = nodes(i, 1);
    y = nodes(i, 2);
    
    if abs(x) < tol || abs(x - L) < tol || abs(y) < tol || abs(y - L) < tol
        boundary_nodes = [boundary_nodes; i];
    end
end

% 修改矩阵和向量
K_mod = K;
F_mod = F;

% 强加边界条件
for i = 1:length(boundary_nodes)
    idx = boundary_nodes(i);
    
    % 将边界节点对应的行和列清零，对角线设为1
    K_mod(idx, :) = 0;
    K_mod(:, idx) = 0;
    K_mod(idx, idx) = 1;
    
    % 将载荷向量对应位置设为零
    F_mod(idx) = 0;
end
end

5. 电场计算函数

由电势的负梯度可以得到电场强度。

Matlab 复制代码

function [Ex, Ey, elem_centers] = compute_electric_field(nodes, elements, phi)
%COMPUTE_ELECTRIC_FIELD 计算电场强度

n_elements = size(elements, 1);
Ex = zeros(n_elements, 1);
Ey = zeros(n_elements, 1);
elem_centers = zeros(n_elements, 2);

for e = 1:n_elements
    % 获取单元节点和电势值
    node_indices = elements(e, :);
    element_nodes = nodes(node_indices, :);
    phi_element = phi(node_indices);
    
    % 计算形状函数导数
    x = element_nodes(:, 1);
    y = element_nodes(:, 2);
    area = abs((x(2)-x(1))*(y(3)-y(1)) - (x(3)-x(1))*(y(2)-y(1))) / 2;
    
    % 避免面积为零的情况
    if area < eps
        continue;
    end
    
    b = zeros(3, 1);
    c = zeros(3, 1);
    b(1) = y(2) - y(3);
    b(2) = y(3) - y(1);
    b(3) = y(1) - y(2);
    
    c(1) = x(3) - x(2);
    c(2) = x(1) - x(3);
    c(3) = x(2) - x(1);
    
    B = [b(1), b(2), b(3);
         c(1), c(2), c(3)] / (2 * area);
    
    % 计算电场（E = -∇φ）
    grad_phi = B * phi_element;
    Ex(e) = -grad_phi(1);
    Ey(e) = -grad_phi(2);
    
    % 计算单元中心坐标
    elem_centers(e, :) = mean(element_nodes);
end

% 移除任何可能包含NaN的值
valid_idx = ~isnan(Ex) & ~isnan(Ey);
Ex = Ex(valid_idx);
Ey = Ey(valid_idx);
elem_centers = elem_centers(valid_idx, :);
end

6. 结果可视化函数

最后，我们通过图形来展示我们的仿真结果。我们将绘制电势分布、电场强度大小、电场矢量图、等势线、3D电势表面和电荷密度分布。

Matlab 复制代码

function visualize_results(nodes, elements, phi, Ex, Ey, elem_centers, L, rho)
%VISUALIZE_RESULTS 可视化仿真结果

figure('Position', [100, 100, 1200, 800], 'Color', 'white');

% 确保phi是列向量
if size(phi, 1) < size(phi, 2)
    phi = phi';
end

% 确保rho是列向量
if size(rho, 1) < size(rho, 2)
    rho = rho';
end

% 子图1：电势分布 - 使用tri = delaunay(nodes(:,1), nodes(:,2))
subplot(2, 3, 1);
tri = delaunay(nodes(:,1), nodes(:,2));
trisurf(tri, nodes(:,1), nodes(:,2), phi, 'EdgeColor', 'none', 'FaceAlpha', 0.8);
title('电势分布 (φ)', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('x (m)'); ylabel('y (m)'); zlabel('电势 (V)');
colorbar;
colormap('jet');
view(2);  % 俯视图
axis equal;
grid on;

% 子图2：电场强度大小
subplot(2, 3, 2);
E_mag = sqrt(Ex.^2 + Ey.^2);
if ~isempty(elem_centers)
    scatter(elem_centers(:,1), elem_centers(:,2), 40, E_mag, 'filled');
end
title('电场强度大小 |E|', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('x (m)'); ylabel('y (m)');
colorbar;
axis equal;
xlim([0, L]); ylim([0, L]);
grid on;

% 子图3：电场矢量图
subplot(2, 3, 3);
if ~isempty(elem_centers) && ~isempty(Ex) && ~isempty(Ey)
    % 归一化电场强度以便更好地显示矢量
    scale_factor = 0.05 * L / max(sqrt(Ex.^2 + Ey.^2) + eps);
    quiver(elem_centers(:,1), elem_centers(:,2), ...
           Ex*scale_factor, Ey*scale_factor, 0, 'LineWidth', 1);
end
title('电场矢量图', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('x (m)'); ylabel('y (m)');
axis equal;
xlim([0, L]); ylim([0, L]);
grid on;

% 子图4：等势线
subplot(2, 3, 4);
% 使用contour函数替代tricontour
x_vals = linspace(0, L, 50);
y_vals = linspace(0, L, 50);
[X, Y] = meshgrid(x_vals, y_vals);
% 插值到规则网格
F_phi = scatteredInterpolant(nodes(:,1), nodes(:,2), phi, 'natural', 'none');
Z = F_phi(X, Y);
contourf(X, Y, Z, 20, 'LineStyle', 'none');
title('等势线', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('x (m)'); ylabel('y (m)');
colorbar;
axis equal;
grid on;

% 子图5：3D电势表面
subplot(2, 3, 5);
trisurf(tri, nodes(:,1), nodes(:,2), phi, 'EdgeColor', 'none', 'FaceAlpha', 0.8);
title('3D电势分布', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('x (m)'); ylabel('y (m)'); zlabel('电势 (V)');
colorbar;
view(30, 30);  % 3D视角
grid on;

% 子图6：电荷密度分布
subplot(2, 3, 6);
trisurf(tri, nodes(:,1), nodes(:,2), rho, 'EdgeColor', 'none', 'FaceAlpha', 0.8);
title('电荷密度分布 (ρ)', 'FontSize', 12, 'FontWeight', 'bold');
xlabel('x (m)'); ylabel('y (m)'); zlabel('ρ (C/m²)');
colorbar;
view(2);  % 俯视图
axis equal;
grid on;

sgtitle('电磁场有限元仿真结果', 'FontSize', 16, 'FontWeight', 'bold');

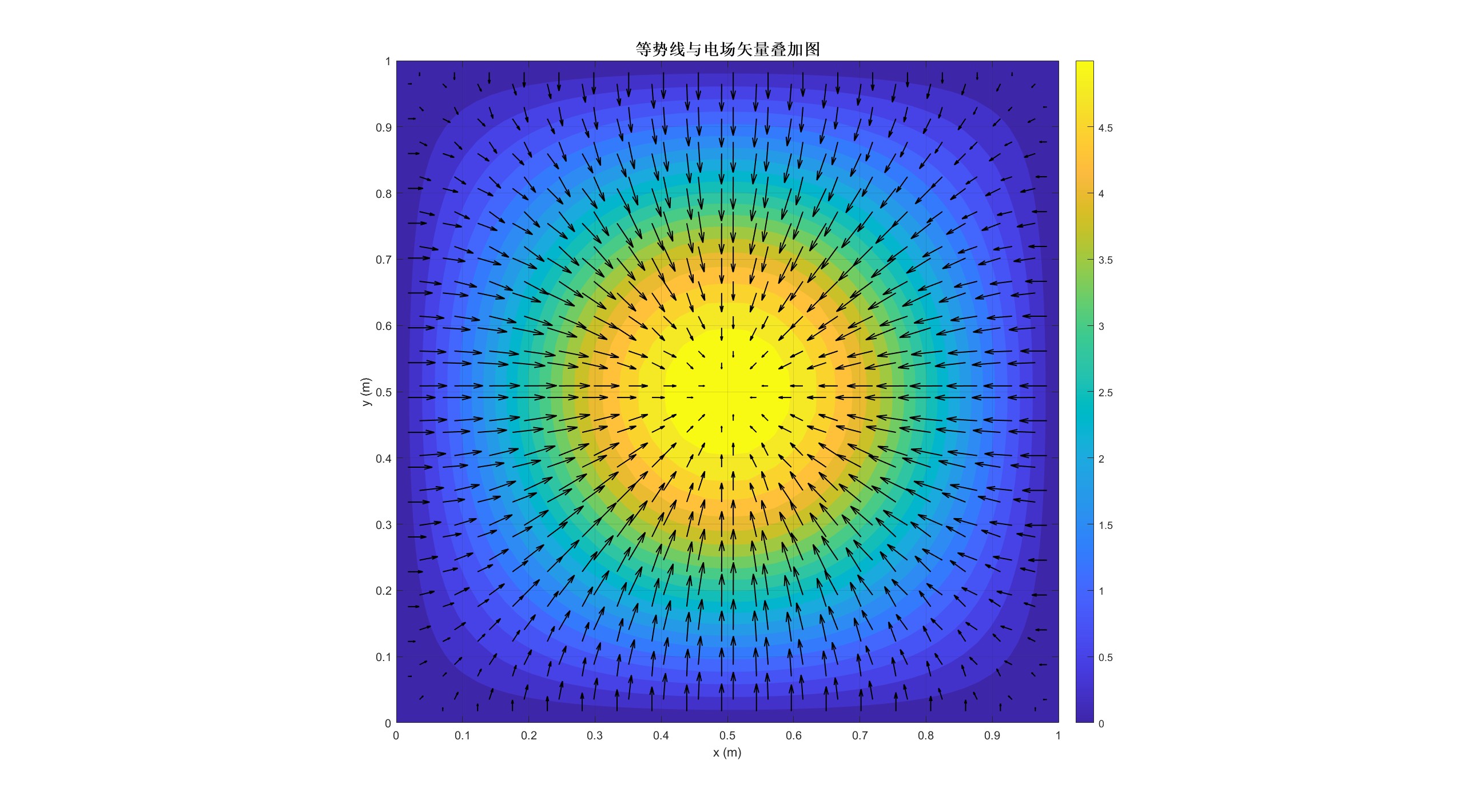
% 添加另一个图：电势和电场的综合图
figure('Position', [100, 100, 800, 600], 'Color', 'white');

% 等势线叠加电场矢量
contourf(X, Y, Z, 20, 'LineStyle', 'none');
hold on;
if ~isempty(elem_centers) && ~isempty(Ex) && ~isempty(Ey)
    scale_factor = 0.05 * L / max(sqrt(Ex.^2 + Ey.^2) + eps);
    quiver(elem_centers(:,1), elem_centers(:,2), ...
           Ex*scale_factor, Ey*scale_factor, 0, ...
           'k', 'LineWidth', 1, 'MaxHeadSize', 1);
end
title('等势线与电场矢量叠加图', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('x (m)'); ylabel('y (m)');
colorbar;
axis equal;
xlim([0, L]); ylim([0, L]);
grid on;
hold off;

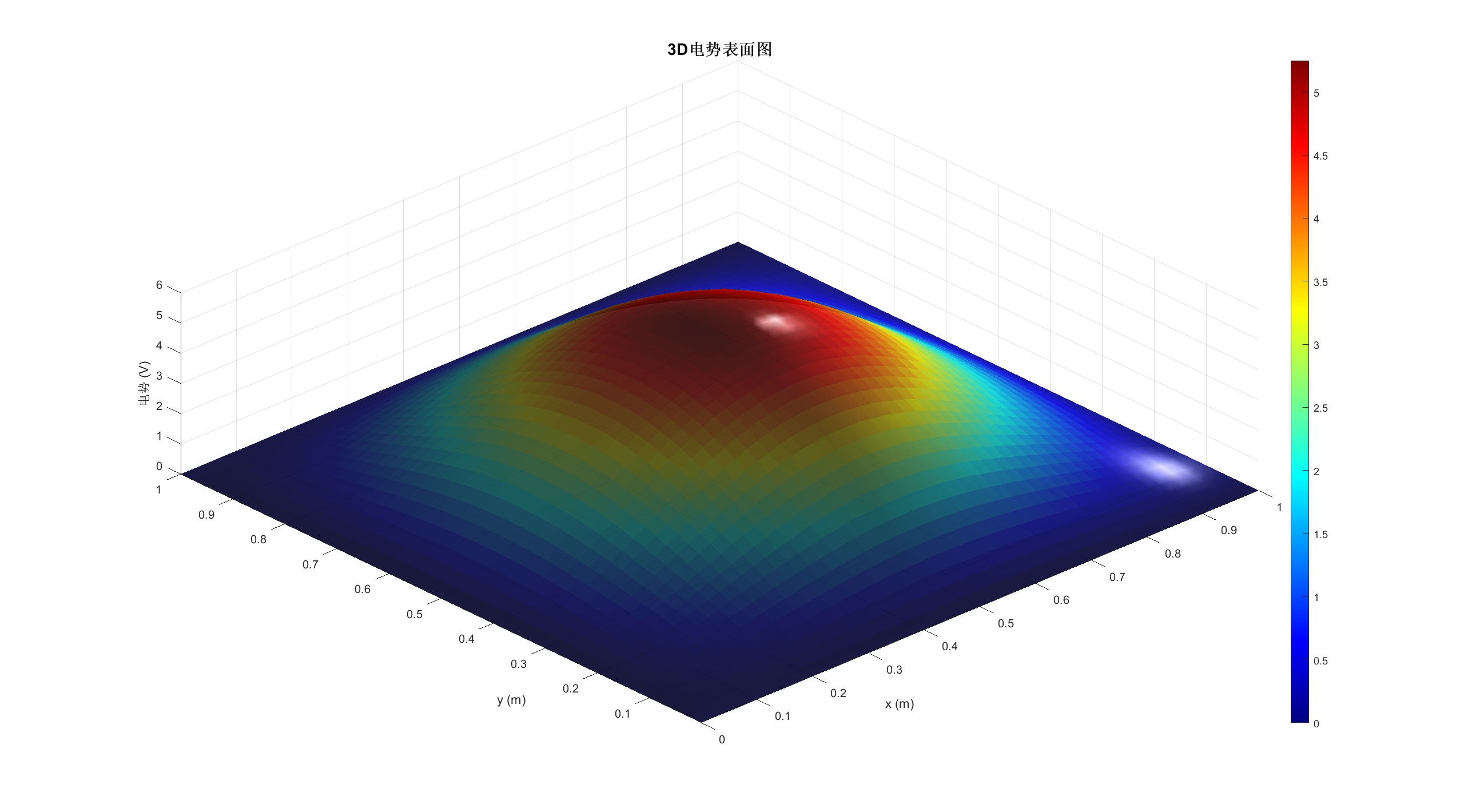
% 添加另一个图：电势的3D表面图
figure('Position', [200, 200, 800, 600], 'Color', 'white');
surf(X, Y, Z, 'EdgeColor', 'none', 'FaceAlpha', 0.9);
title('3D电势表面图', 'FontSize', 14, 'FontWeight', 'bold');
xlabel('x (m)'); ylabel('y (m)'); zlabel('电势 (V)');
colormap('jet');
colorbar;
view(40, 30);
grid on;
light;
lighting gouraud;
material shiny;
end

7. 总能量计算函数

Matlab 复制代码

function total_energy = compute_total_energy(K, phi)
%COMPUTE_TOTAL_ENERGY 计算系统总能量
%   总能量 = 0.5 * φ^T * K * φ

total_energy = 0.5 * (phi' * K * phi);
end

最终代码的运行结果：

=================== 电磁场有限元仿真开始 ===================

正在生成网格...

网格生成完成：400 个节点，722 个单元

正在设置电荷分布...

正在组装系统矩阵...

正在应用边界条件...

正在求解线性方程组...

电势求解成功！电势范围：[0.0000e+00, 5.2488e+00] V

正在计算电场强度...

正在生成可视化结果...

正在计算系统总能量...

系统总能量: 5.3855e-10 J

平均电场强度: 1.0460e+01 V/m

=================== 电磁场有限元仿真完成 ===================

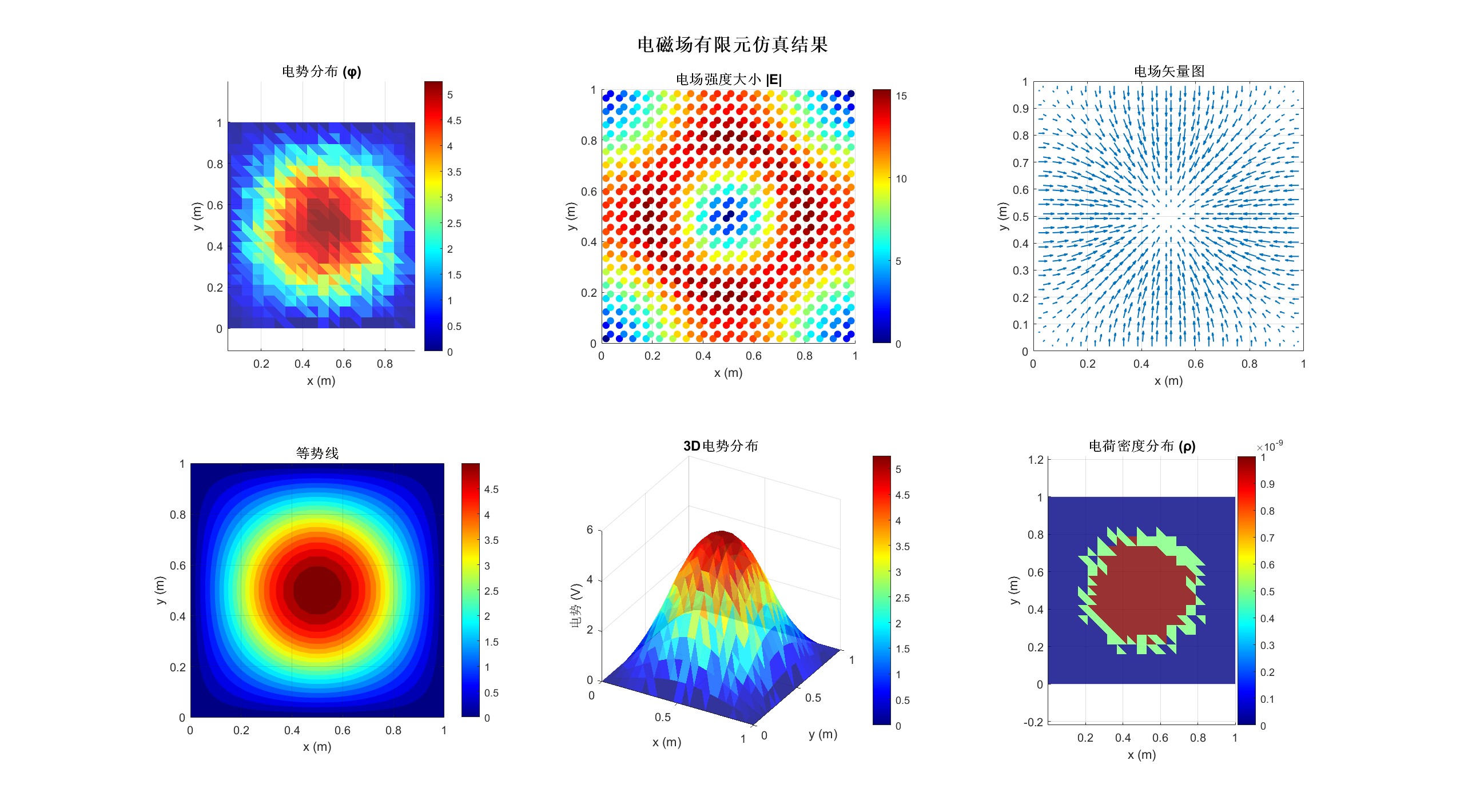
运行上述代码后，我们得到了一个包含6个子图的综合结果。从这些图中，我们可以清晰地看到：

电势分布：中心区域电势较高，向边界逐渐降低，边界处为零（因为我们设定了接地边界条件）。
电场强度大小：在电荷密度高的区域，电场强度也较大。
电场矢量图：电场方向从高电势指向低电势，即从中心指向边界。
等势线：等势线呈同心圆状，因为我们的电荷分布是中心对称的。
3D电势表面：电势在中心隆起，向边界平滑下降。
电荷密度分布：展示了我们设定的电荷密度分布情况。

通过这个简单的例子，我们完成了二维静电场的有限元仿真。虽然问题相对简单，但它涵盖了有限元方法的核心步骤：网格生成、系统组装、边界条件处理、求解和可视化。希望这个例子能激发你对电磁场仿真和有限元方法的兴趣。你可以尝试修改电荷密度分布、边界条件或几何形状，来探索不同的仿真场景。

记住，仿真不仅仅是编程，它更是一种理解物理现象的方式。通过调整参数并观察结果，可以获得对电磁场行为的直观理解。

三、脚本代码：

Matlab 复制代码

%##################################################################################
%matlab
%20251201
%ex_EM_FEM
%二维静电场有限元仿真（泊松方程）
%求解区域：单位正方形，边界条件：狄利克雷边界条件
%方程：-∇·(ε∇φ) = ρ，其中φ为电势，ε为介电常数，ρ为电荷密度
%##################################################################################
close all
clear
clc

%##################################################################################
fprintf('=================== 电磁场有限元仿真开始 ===================\n');

% 参数设置
epsilon = 8.854e-12;  % 真空介电常数
L = 1;                % 区域尺寸（正方形边长）
num_nodes_x = 20;     % x方向节点数
num_nodes_y = 20;     % y方向节点数

% 生成网格
fprintf('正在生成网格...\n');
[nodes, elements] = generate_mesh(L, num_nodes_x, num_nodes_y);
num_nodes = size(nodes, 1);
num_elements = size(elements, 1);
fprintf('网格生成完成：%d 个节点，%d 个单元\n', num_nodes, num_elements);

% 设置电荷密度分布（示例：中心区域有正电荷）
fprintf('正在设置电荷分布...\n');
rho = set_charge_density(nodes, L);

% 应用边界条件
fprintf('正在组装系统矩阵...\n');
[K, F] = assemble_system(nodes, elements, epsilon, rho);
fprintf('正在应用边界条件...\n');
[K_modified, F_modified] = apply_boundary_conditions(nodes, K, F, L);

% 求解线性方程组
fprintf('正在求解线性方程组...\n');
phi = K_modified \ F_modified;

% 检查phi是否全是零或NaN
if all(phi == 0)
    warning('所有节点的电势都是零！检查边界条件。');
elseif any(isnan(phi))
    error('电势计算出现NaN值！检查矩阵组装和求解过程。');
else
    fprintf('电势求解成功！电势范围：[%.4e, %.4e] V\n', min(phi), max(phi));
end

% 计算电场强度
fprintf('正在计算电场强度...\n');
[Ex, Ey, elem_centers] = compute_electric_field(nodes, elements, phi);

% 可视化结果
fprintf('正在生成可视化结果...\n');
visualize_results(nodes, elements, phi, Ex, Ey, elem_centers, L, rho);

% 计算总能量
fprintf('正在计算系统总能量...\n');
total_energy = compute_total_energy(K, phi);
fprintf('系统总能量: %.4e J\n', total_energy);

% 计算平均电场强度
avg_E_mag = mean(sqrt(Ex.^2 + Ey.^2));
fprintf('平均电场强度: %.4e V/m\n', avg_E_mag);

fprintf('=================== 电磁场有限元仿真完成 ===================\n');
format short
%#############################End##################################################