一、二叉搜索树的概念
1、概念
二叉搜索树其又叫二叉查找树,二叉排序树,二叉有序树等。
其是指的一棵空树,或者具有下面几个性质的二叉树:
1、若它的左子树不为空,那么左子树上的所有节点的值都小于它的根节点的值。
2、若它的右子树不为空,那么右子树上的所有节点的值都大于它的根节点的值。
3、而且其左右子树也都是二叉搜索树。
4、然后二叉搜索树可以支持插入相等的值,也可以不支持插入相等的值,这个我们要看我们的使 用场景来决定。后续我们还会学习map/set/multimap/multiset系列容器的时候底层就是二叉搜 索树,其中map/set是不支持插入相等的值的,multimap/multiset就支持相等的值。
综上所述:
二叉搜索树就是其任意一个节点,其左边的节点的值要比其小,然后右边节点的值要比其大。然后我们插入数据也要遵循这个原则,然后就是我们要查找数据的时候可以将要查找的数据和根节点的值开始比较,要是比根节点的大,那么就去其右边子树查找,如此往复,,直到查找到,或者到这个节点为空。要是比根节点的要小,那么就去左子树查找。
如下图就是一个二叉搜索树:
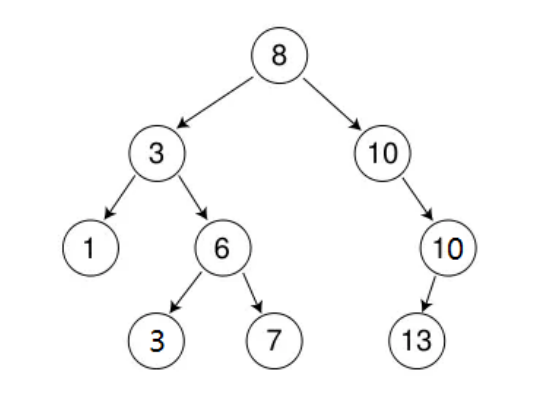
2、二叉搜索树的性能分析
首先就是最优的情况:二叉搜索树为完全二叉树或者接近完全二叉树的状态,这个时候其查找的时间复杂度就是其树高度了log2N。
然后最差的情况就是其为单支树的情况(或者类似单支树),如下所示:
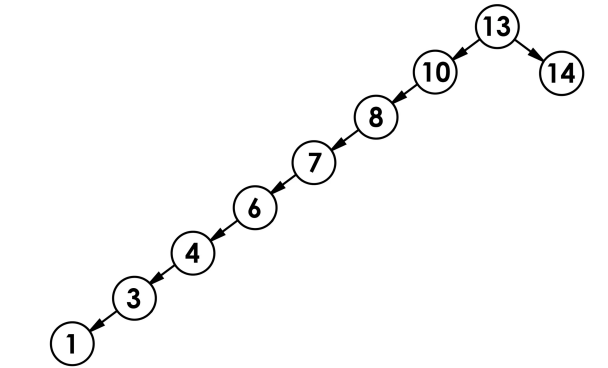
这个时候的时间复杂度就为O(n)了。
所以总的来说二叉搜索树的增删查改的时间复杂度为O(n)。
所以其效率还是比较低的,后续我们学习平衡二叉搜索树AVL树红黑树,这几个的效率就高,才适合我们在内存中存储数据和查找数据。
二、二叉搜索树的实现
1、二叉搜索树的基本结构
我们的二叉搜索树其主要由要存储的数据,然后指向左右节点的指针构成:
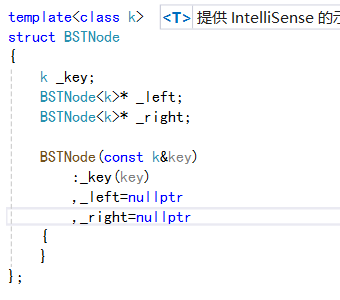
2、二叉搜索树的插入
二叉搜索树的插入,首先要注意的是,我们插入的位置一定是一个叶子节点,然后我们此处实现的是不支持插入相等值的二叉搜索树。
我们将插入数据函数的返回值类型设置为bool类型,然后对于插入的数据是相同的,那么我们直接返回flase,然后数据插入完成,我们就返回true。
那么下面我们看看二叉搜索树的数据插入逻辑是咋样的:
要是树是空的,那么就直接插入数据即可,使用这个数据新开一个节点,然后将指向根节点的指针_root指向这个新开的节点即可。
然后第二种情况就是树不为空,那么我们就要将要插入的数据和节点的数据进行比较了,首先将其和根节点的数据进行比较,要是要插入的数据大,那么我们就去右子树再进行比较,要是其比根节点的数据小,那么就去左子树找,,反复即可。
那么我们听到上面的逻辑,那么就有同学会想到使用递归的方式进行寻找插入的位置了。
我们前面学习C语言的时候讲过,递归的目的是将复杂的问题简单化,但是函数递归,会导致堆栈,其开支很大,很容易导致栈溢出。
所以二叉搜索树的数据插入我们使用循环来解决:
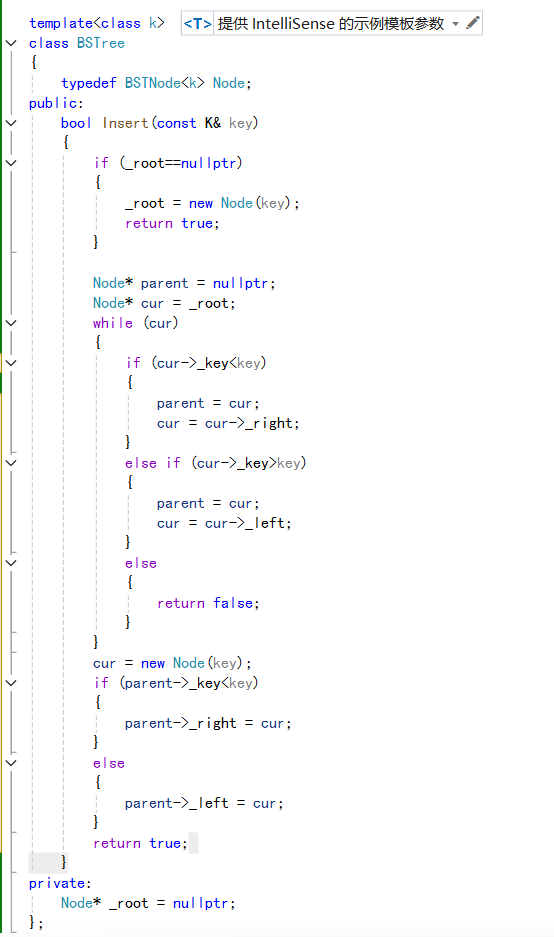
如上所示就是我们的插入函数了,我们再从代码来理理其逻辑。
上面我们多创建了一个parent指针,要是没有这个指针,那么当我们的cur指针走到空的时候,这时候要插入的位置是找到了,但是我们发现我们无法插入数据,我们此时修改cur是没办法完成数据的插入的,当函数运行完成后,其就销毁了。所以我们创建一个parent指针是为了存储cur的父节点,然后通过parent进行修改其的左右指针。
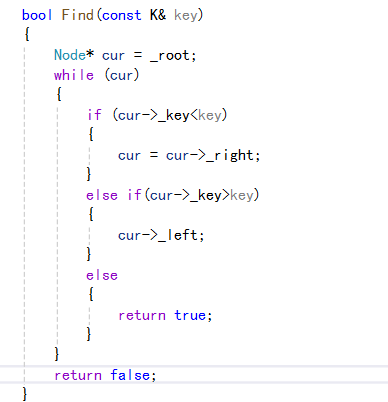
3、数据的查找
二叉搜索树的查找,就和插入有点像,我们根据传入的参数,然后将其和节点指向的数据进行比较,要是相等,那么就返回true,然后要是不相等,那么就将其和节点的数据比大小,要是要查找的数据大,,那么就去其右节点寻找,然后重复上面的步骤。要是小于的话,就去左边子树进行比较。
4、二叉搜索树的删除
首先我们要确定树中有这个数据才行,所以先确定在树中有这个数据才能进行删除操作。
然后就可以进行我们的删除操作了,对于二叉搜索树的删除,我们主要分为下面几种情况:
1、删除的节点是叶子节点,那么这种直接进行删除即可
2、删除的节点只有一个孩子节点
这种情况也不复杂,我们让被删除的节点的父节点指向被删除这个节点的指针指向被删除节点的孩子节点即可,如下:
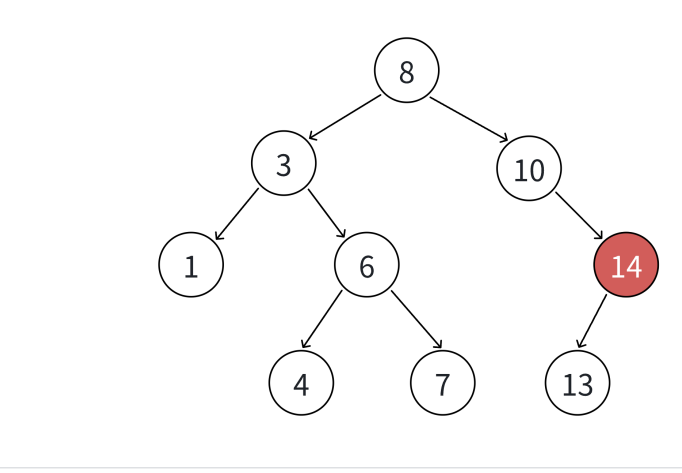
上面这种情况就是删除的节点只有一个孩子的情况,那么我们就将10指向右孩子的指针指向13即可。
3、删除的节点有两个孩子节点
这种情况要比上面两种情况复杂很多,那么我们能不能将这种情况化简成为删除一个孩子节点或者叶子节点的情况呢?
那么我们可以利用其前驱后继看看,在二叉搜索树中,其规则是该节点的右孩子的值要比其大,然后左孩子节点的数据要小。然后二叉搜索树的中序遍历是升序的情况,然后这个节点的前驱后继在中序遍历中刚刚好是其前一个和后一个。
然后一个节点的左子树的值都是比该节点的小,右子树的值都比该节点的要大,然后该子树的最大值就是其最右边的节点,最小值就是最左边的节点。所以一个节点其要是有左右两个子树,那么其前驱就在左子树的最右边节点,后继一定在右边子树的最左边节点。
那么我们很容易可以找到该节点的前驱和后继,那么我们删除的时候,只需要将其前驱或者后继和其交换,然后再删除即可,或者直接将其前驱和后继覆盖掉。
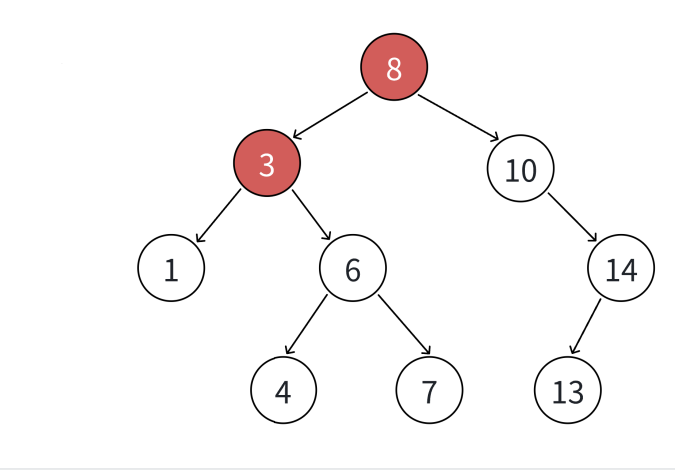
如上图所示,我们要删除8,那么我们可以将其和7这个节点进行交换,然后再进行删除。\
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 准备删除
if (cur->_left == nullptr)
{
if (cur != _root)
{
// 左为空,父亲指向我的右
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
else
{
_root = cur->_right;
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur != _root)
{
// 右为空,父亲指向我的左
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
else
{
_root = cur->_left;
}
delete cur;
}
else
{
// 左右都不为空,找子树中适合的节点替代我
Node* minRightParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minRightParent = minRight;
minRight = minRight->_left;
}
swap(cur->_key, minRight->_key);
if (minRight == minRightParent->_left)
{
minRightParent->_left = minRight->_right;
}
else
{
minRightParent->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}5、二叉搜索树的中序遍历
为啥我们要专门讲其的中序遍历呢?
前面学习二叉树的时候,我们讲了三种遍历方式,为啥我们专门拿中序遍历出来讲呢。
这是因为二叉搜索树的中序遍历后,其遍历的结果是有序的,而且是升序的。
然后就是我们的二叉搜索树的头节点是私有的,那么我们在外部是没法获取到头节点的地址的,那么我们可以如下这样操作:

三、二叉搜索树实现完整代码
#pragma once
#include<iostream>
using namespace std;
template<class k>
struct BSTNode
{
k _key;
BSTNode<k>* _left;
BSTNode<k>* _right;
BSTNode(const k&key)
:_key(key)
,_left=nullptr
,_right=nullptr
{
}
};
template<class k>
class BSTree
{
typedef BSTNode<k> Node;
public:
bool Insert(const k& key)
{
if (_root==nullptr)
{
_root = new Node(key);
return true;
}
//节点插入
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key<key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key>key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key);
if (parent->_key<key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
//查找
bool Find(const k& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key<key)
{
cur = cur->_right;
}
else if(cur->_key>key)
{
cur->_left;
}
else
{
return true;
}
}
return false;
}
//节点删除
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 准备删除
if (cur->_left == nullptr)
{
if (cur != _root)
{
// 左为空,父亲指向我的右
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
else
{
_root = cur->_right;
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur != _root)
{
// 右为空,父亲指向我的左
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
else
{
_root = cur->_left;
}
delete cur;
}
else
{
// 左右都不为空,找子树中适合的节点替代我
Node* minRightParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minRightParent = minRight;
minRight = minRight->_left;
}
swap(cur->_key, minRight->_key);
if (minRight == minRightParent->_left)
{
minRightParent->_left = minRight->_right;
}
else
{
minRightParent->_right = minRight->_right;
}
delete minRight;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};四、二叉搜索树的key与key-value搜索场景
1、key搜索场景
使用key作为搜索的关键码,然后结构中只存储key,关键码即为需要搜索到的值,搜索场景只需要判断key是否存在。key的搜索场景实现的⼆叉树搜索树⽀持增删查,但是不⽀持修改,修改key破坏搜索树结 构了。
场景1:
小区的无人值守车库,小区车库买了车位的车主才能进入小区,然后物业会有一个文件,将买了车位的车主录入这个文件中,那么车辆进入小区的时候,会先在这个文件中进行查找。
要是存在,那么就允许进入,要是不存在就不允许进入。
场景2:
检查一篇英文文章单词拼写是否正确,然后将词库中所有单词放入二叉搜索树,读取文章中的单词,检查是否在二叉搜索树中。
2、key/value搜索场景
每⼀个关键码key,都有与之对应的值value,value可以任意类型对象。树的结构中(结点)除了需要存 储key还要存储对应的value,增/删/查还是以key为关键字⾛⼆叉搜索树的规则进⾏⽐较,可以快速查找到key对应的value。key/value的搜索场景实现的⼆叉树搜索树⽀持修改,但是不⽀持修改key,修 改key破坏搜索树性质了,可以修改value。
场景1:简单中英互译字典,树的结构中(结点)存储key(英⽂)和vlaue(中⽂),搜索时输⼊英⽂,则同时 查找到了英⽂对应的中⽂。
场景2:商场⽆⼈值守⻋库,⼊进场时扫描⻋牌,记录⻋牌和⼊场时间,出离场时,扫描⻋牌,查 找⼊场时间,⽤当前时间-⼊场时间计算出停⻋时⻓,计算出停⻋费⽤,缴费后抬杆,⻋辆离场。
场景3:统计⼀篇⽂章中单词出现的次数,读取⼀个单词,查找单词是否存在,不存在这个说明第⼀次 出现,(单词,1),单词存在,则++单词对应的次数。
下面是上面这些问题的实现代码:
// key
template<class K, class V>
class BSTree
{
typedef BSTNode<K, V> Node;
public:
bool Insert(const K& key, const V& value)
{
if (_root == nullptr)
{
_root = new Node(key, value);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(key, value);
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}
Node* Find(const K& key)
{
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
else
{
return cur;
}
}
return nullptr;
}
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 准备删除
if (cur->_left == nullptr)
{
if (cur != _root)
{
// 左为空,父亲指向我的右
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
else
{
_root = cur->_right;
}
delete cur;
}
else if (cur->_right == nullptr)
{
if (cur != _root)
{
// 右为空,父亲指向我的左
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
else
{
_root = cur->_left;
}
delete cur;
}
else
{
// 左右都不为空,找子树中适合的节点替代我
Node* minRightParent = cur;
Node* minRight = cur->_right;
while (minRight->_left)
{
minRightParent = minRight;
minRight = minRight->_left;
}
swap(cur->_key, minRight->_key);
if (minRight == minRightParent->_left)
minRightParent->_left = minRight->_right;
else
minRightParent->_right = minRight->_right;
delete minRight;
}
return true;
}
}
return false;
}
void InOrder()
{
_InOrder(_root);
cout << endl;
}
private:
void _InOrder(Node* root)
{
if (root == nullptr)
return;
_InOrder(root->_left);
cout << root->_key << ":" << root->_value << endl;
_InOrder(root->_right);
}
private:
Node* _root = nullptr;
};