1. 课程设计目的
《软件设计基础-C++》课程设计是这门课程的实践性教学环节之一,本次设计结合实际应用的要求,使课程设计既覆盖C的知识点,又接近工程实际需要。目的是通过课程设计的综合训练,培养学生实际分析问题、解决问题的能力,以及编程和动手能力,最终目标是通过课程设计这种形式,帮助学生系统掌握C这门课程的主要内容,养成良好的编程习惯,更好的完成教学任务。
2. 课程设计任务与要求
要求:
本次课程设计利用《软件设计基础-C++》课程中所学到的编程知识和编程技巧,完成具有一定难度和工作量的程序设计题目,帮助学生掌握编程、调试的基本技能,独立完成所布置的任务。
要求:
- 对系统进行功能需求分析
- 设计合理的数据结构和系统框架
- 界面设计美观、清楚、合理
- 编程简练,程序功能齐全,能正确运行
- 具有一定的创新性
- 说明书、流程图要清楚
- 课题完成后必须按要求提交课程设计报告
任务:
- 矩阵的加法
- 矩阵的乘法
- 矩阵的转置
- 矩阵的对角线求和
3.课程设计说明书
⑴功能描述
- 计算两个矩阵的加法
- 计算两个矩阵的乘法
- 计算矩阵的转置
- 计算矩阵的对角线的和
⑵概要设计
模块结构图:
根据功能分析,建立自制矩阵实验室系统的体系结构,即将整个系统分解成五个模块,用框图表示如下:
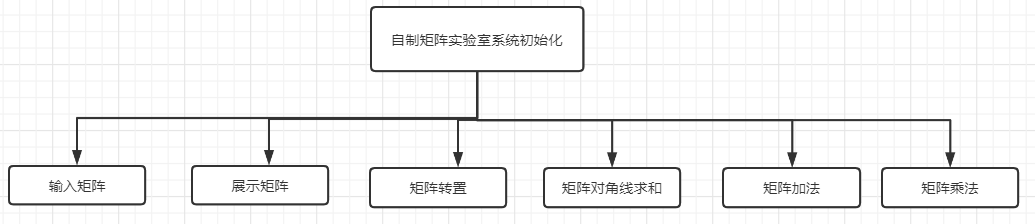
⑶详细设计
总体流程图如下:
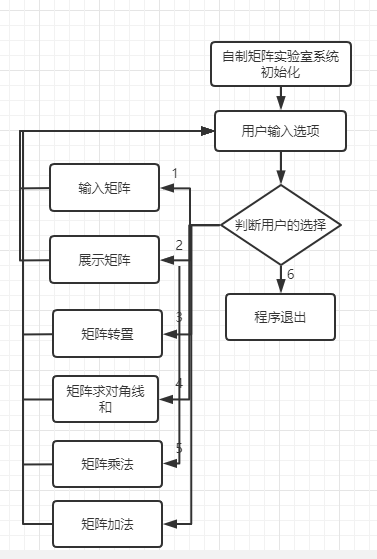
各个功能模块流程图:
由于其他功能过于简单,这里列出几个核心的功能,核心的矩阵乘法流程图如下:
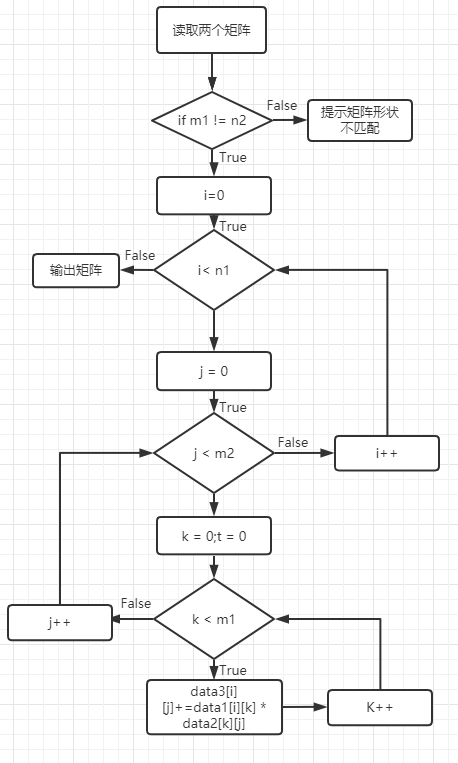
核心的矩阵转置流程图如下:
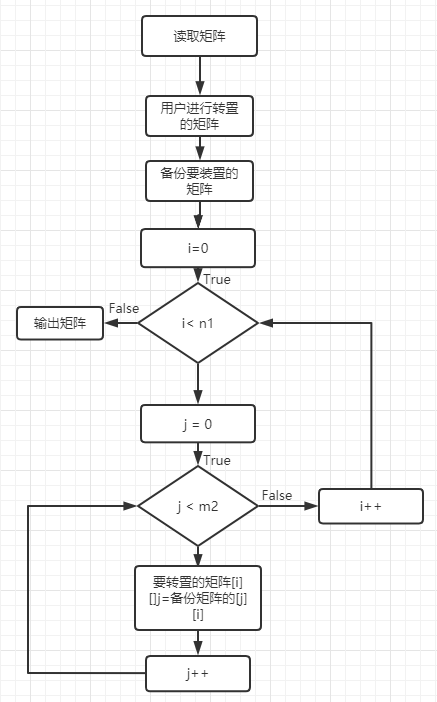
⑷代码实现
本系统共包含5个小功能:详细如下:
输入并储存矩阵
作用:提示用户输入矩阵
设计思路:使用两个二维数组来存储两个矩阵,使用两个for循环来录入一个矩阵
代码如下:
void read_matrix(){
cout << "请输入矩阵1的大小:(空格隔开)" << endl;
cin >> n1 >> m1;
cout << "请输入矩阵1的数据:(空格隔开)" << endl;
for( i = 0; i < n1;i++){
for( j = 0; j < m1;j++){
cin >> data1[i][j];
}
}
cout << "请输入矩阵2的大小:(空格隔开)" << endl;
cin >> n2 >> m2;
cout << "请输入矩阵2的数据:(空格隔开)" << endl;
for( i = 0; i < n2;i++){
for( j = 0; j < m2;j++){
cin >> data2[i][j];
}
}
}矩阵加法
作用:将两个矩阵进行相加
设计思路:使用一个二维矩阵来存储结果,然后使用双重循环结构进行对应元素的相加。
代码如下:
void matrix_add(){
cout << "矩阵1+矩阵2" << endl;
if(n1 != n2 || m1 != m2){
cout << "矩阵形状不匹配!!!";
return;
}
for( i = 0; i < n1;i++){
for( j = 0; j < m1;j++){
data3[i][j] = data1[i][j] + data2[i][j];
}
}
cout << "相加后的结果是:" << endl;
for( i = 0; i < n1;i++){
for( j = 0; j < m1;j++){
cout << data3[i][j] << " ";
}
cout << endl;
}
}矩阵转置
作用:将单个矩阵进行转置
设计思路:使用一个临时二维矩阵来将要转置的矩阵,原矩阵[i][j]=临时二维矩阵[j][j]
代码如下:
cout << "请输入你想转置的矩阵:(1或2)" << endl;
int choose;
cin >> choose;
if(choose == 1){
for( i = 0; i < n1;i++){
for( j = 0; j < m1;j++){
data3[i][j] = data1[j][i];
}
}
cout << "转置完的data1矩阵为(矩阵会原地更新):" << endl;
for( i = 0; i < n1;i++){
for( j = 0; j < m1;j++){
data1[i][j] = data3[i][j];
cout << data1[i][j] << " ";
}
cout << endl;
}
}
if(choose == 2){
for( i = 0; i < n1;i++){
for( j = 0; j < m1;j++){
data3[i][j] = data2[i][j];
}
}
cout << "转置完的data2矩阵为(矩阵会原地更新):" << endl;
for( i = 0; i < n1;i++){
for( j = 0; j < m1;j++){
data2[i][j] = data3[j][i];
cout << data2[i][j] << " ";
}
cout << endl;
}
}
}矩阵对角线求和
作用:计算矩阵的主对角线和副对角线的和
设计思路:使用两个变量来存储结果,然后通过双重循环结构进行对角线元素的相加。
代码如下:
void matrix_sum(){
// 矩阵对角线求和
cout << "请输入你想对角线求和的矩阵:(1或2)" << endl;
int choose;
cin >> choose;
double zhu,fu;
zhu=fu=0;
if(choose == 1){
for(i = 0; i < n1;i++){
zhu += data1[i][i];
fu += data1[i][n1-i - 1];
}
} else{
for(i = 0; i < n1;i++){
zhu += data2[i][i];
fu += data2[i][n2-i-1];
}
}
cout << "主对角线求和为:" << zhu << endl;
cout << "副对角线求和为:" << fu << endl;
}矩阵乘法
作用:计算两个矩阵的乘积
设计思路:先创建一个结果矩阵。然后使用第一个for循环遍历结果矩阵的行,使用第二个for循环遍历矩阵的列,使用第三个for循环来遍历被乘矩阵的行,使用t来不断加等于data1[i][k]*data2[k][j]
代码如下:
void matrix_muti(){
if(m1 != n2){
cout << "矩阵形状不匹配!!!";
return;
}
for(i = 0; i < n1; i++){
forint j = 0; j < m2; j++){
double t = 0;
for(k = 0; k < m1; k++){
// cout << data1[i][k] << " " << data2[j][k] << endl;
t += data1[i][k] * data2[k][j];
}
data3[i][j] = t;
}
}
cout << "最后的矩阵乘积是:" << endl;
for(i = 0; i < n1; i++){
for(j = 0; j < m2; j++){
cout << data3[i][j] << " ";
}
cout << endl;
}
}4. 课程设计成果
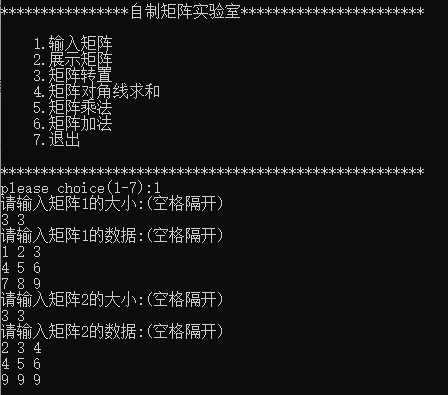
输入矩阵
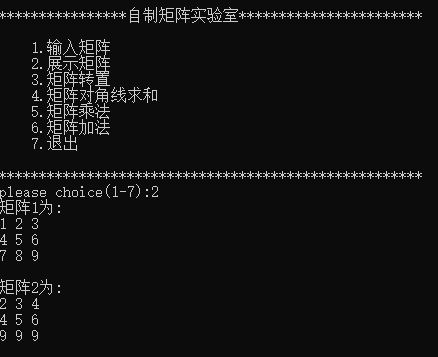
展示矩阵
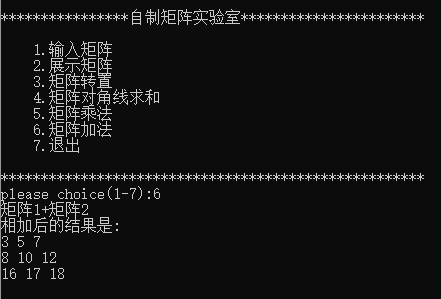
矩阵加法
矩阵求和

矩阵乘法

矩阵转置
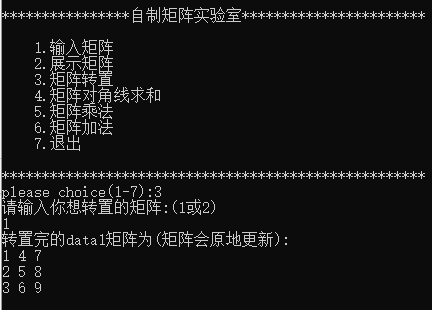
5. 程序调试过程
程序调试的步骤,首先将程序分成5个模块,逐模块的去实现,实现一个模块调试一个模块,最终在调试完所有的模块之后进行编写主函数,其中开始的测试函数代码如下所示:
int test(){
freopen("data.in","r",stdin);
read_matrix();
matrix_show();
matrix_T();
matrix_sum();
matrix_muti();
}本次程序并没有遇到太大的问题。
6. 设计问题的不足和改进方案
本次设计问题的不足有:
- 程序并没有保存结果的功能,导致用户如果关闭程序后,必须重新录入矩阵才能继续进行计算。
- 矩阵在转置时,采用的简单的行列元素互换的方式。其效率要比matlab低。
改进方案:
可以为用户添加保存的功能,以便用户进行保存。
7. 课程设计心得
通过本次实验,我更加理解了计算机的思维,如果要实现一个程序的编写的编写就要清清楚楚知道整个程序的流程,如果不清楚程序的流程是很难顺利流畅的编写出程序来,就例如本次实验中的计算矩阵的乘法,如果只是会死记硬背笔算,其实很难实现出程序来。最终通过本次实验我收获颇多。
8. 参考文献
- 工程数学 线性代数.北京:高等教育出版社,2014.6
- 秋叶拓哉 ,岩田阳一,北川宜稔 挑战程序竞赛.北京:人民邮电出版社,2013.7
- 刘汝佳.算法竞赛入门经典.北京:清华大学出版社,2009.11
- 潘嘉杰.易学C++.北京:人民邮电出版社,2008.6
-
Stephen Prata\]([https://book.douban.com/search/Stephen](https://book.douban.com/search/Stephen "https://book.douban.com/search/Stephen") Prata)/[孙建春](https://book.douban.com/search/%E5%AD%99%E5%BB%BA%E6%98%A5 "孙建春")/[韦强](https://book.douban.com/search/%E9%9F%A6%E5%BC%BA "韦强").C++Primer Plus.北京:人民邮电出版社,2005.5