14. 某马数据结构整理（2）

带土12025-12-02 14:38

4.树和二叉树

4.1树的基本概念

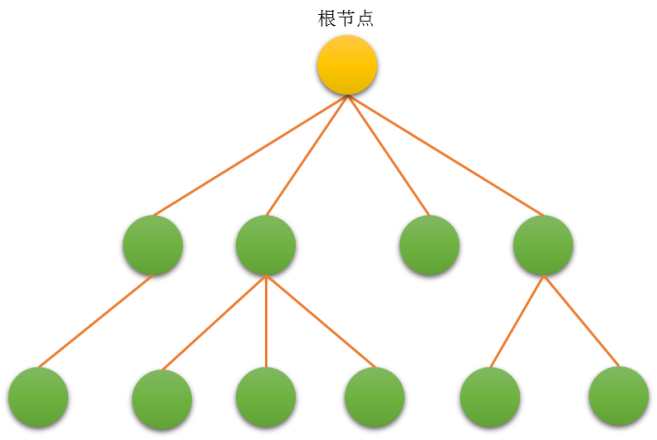
  • 树的定义：

    由一个或多个(n≥0)结点组成的有限集合T，有且仅有一个结点称为根（root），当n>1时，其余的结点分为m(m≥0)个互不相交的有限集合T1,T2，...，Tm。每个集合本身又是棵树，被称作这个根的子树 。

  • 树的结构特点

    • 非线性结构，有一个直接前驱，但可能有多个直接后继（1:n）
    • 树的定义具有递归性，树中还有树。
    • 树可以为空，即节点个数为0。

  • 若干术语

    • 根 即根结点(没有前驱)
    • 叶子 即终端结点(没有后继)
    • 森林 指m棵不相交的树的集合(例如删除A后的子树个数)
    • 有序树 结点各子树从左至右有序，不能互换（左为第一）
    • 无序树 结点各子树可互换位置。
    • 双亲 即上层的那个结点(直接前驱) parent
    • 孩子 即下层结点的子树 (直接后继) child
    • 兄弟 同一双亲下的同层结点（孩子之间互称兄弟）sibling
    • 堂兄弟 即双亲位于同一层的结点（但并非同一双亲）cousin
    • 祖先 即从根到该结点所经分支的所有结点
    • 子孙 即该结点下层子树中的任一结点
    • 结点 即树的数据元素
    • 结点的度 结点挂接的子树数（有几个直接后继就是几度）
    • 结点的层次 从根到该结点的层数（根结点算第一层）
    • 终端结点 即度为0的结点，即叶子
    • 分支结点 除树根以外的结点（也称为内部结点）
    • 树的度 所有结点度中的最大值（Max{各结点的度}）
    • 树的深度(或高度) 指所有结点中最大的层数（Max{各结点的层次}）

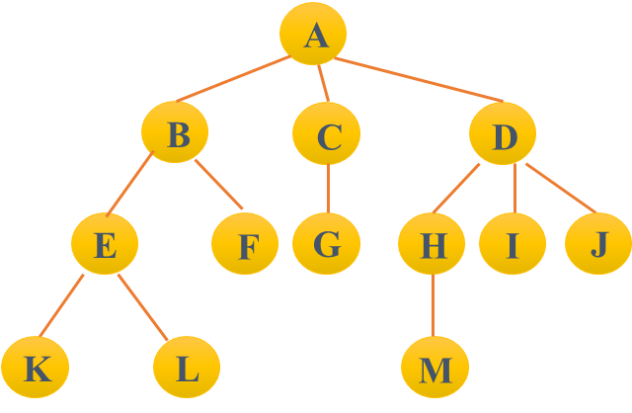
上图中的结点数＝ 13，树的度＝ 3，树的深度＝ 4

4.2树的表示法

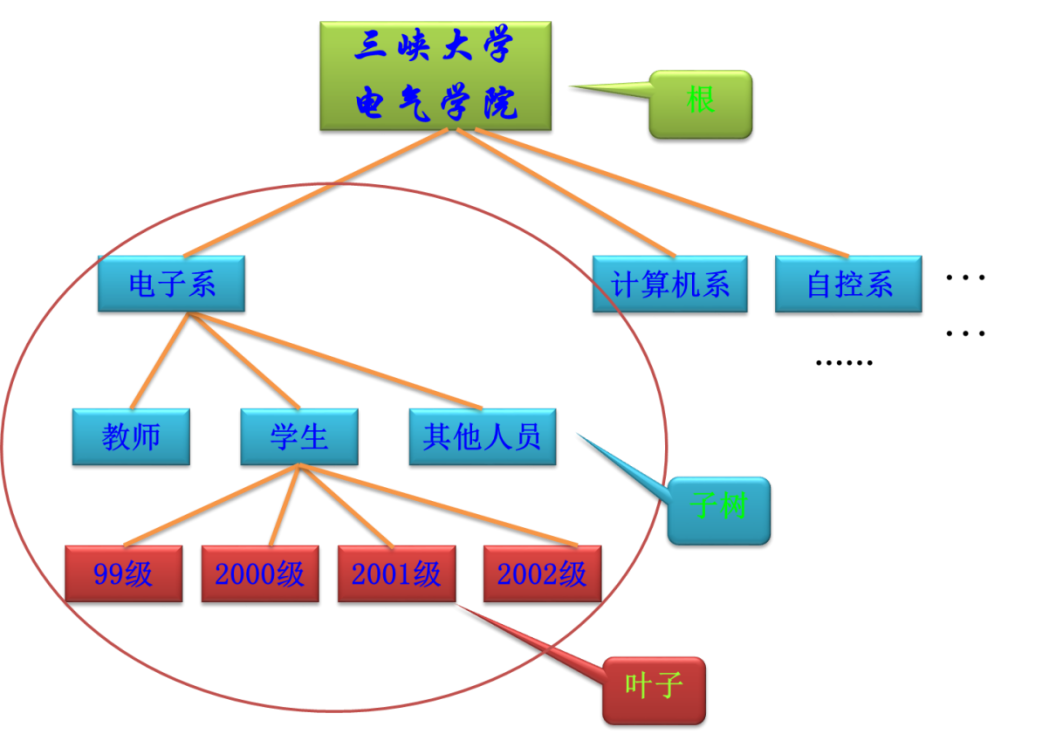
4.2.1图形表示法

事物之间的逻辑关系可以通过数的形式很直观的表示出来，如下图：

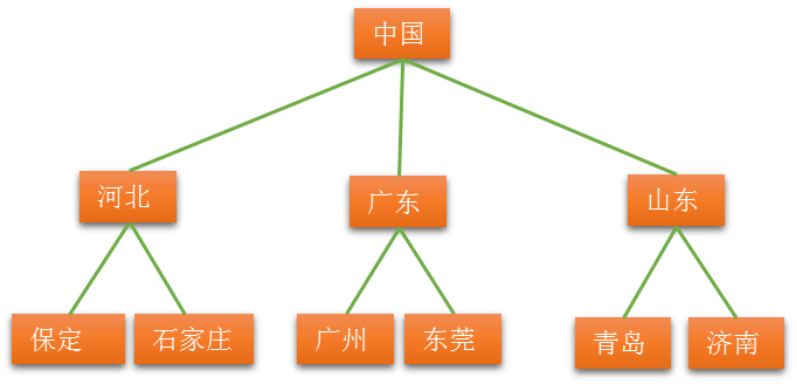
4.2.2广义表表示法

  • 用广义表表示法表示上图：

    中国（河北（保定，石家庄），广东（广州，东莞），山东（青岛，济南））

    根作为由子树森林组成的表的名字写在表的左边。

4.2.3左孩子右兄弟表示法

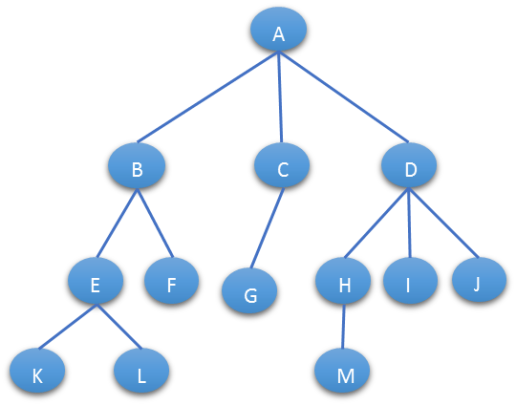
左孩子右兄弟表示法可以将一颗多叉树转化为一颗二叉树：

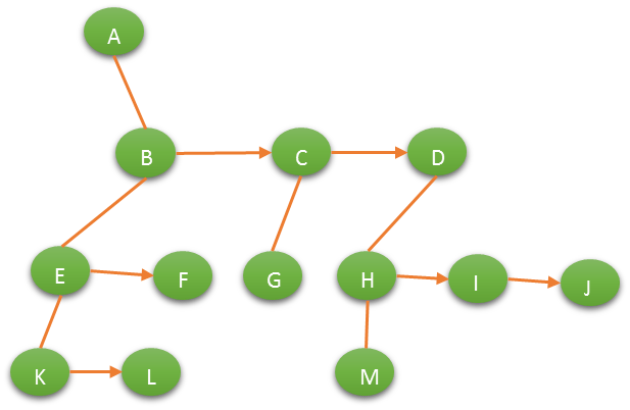
节点的结构：

节点有两个指针域，其中一个指针指向子节点，另一个指针指向其兄弟节点。

4.3二叉树概念

4.3.1二叉树基本概念

  • 定义：

    n（n≥0）个结点的有限集合，由一个根结点以及两棵互不相交的、分别称为左子树和右子树的二叉树组成 。

  • 逻辑结构：

    一对二（1：2）

  • 基本特征:

    每个结点最多只有两棵子树（不存在度大于2的结点）；

    左子树和右子树次序不能颠倒（有序树）。

基本形态:

  • 二叉树性质
    • 性质1: 在二叉树的第i层上至多有2i-1个结点（i>0）
    • 性质2: 深度为k的二叉树至多有2k-1个结点（k>0）
    • 性质3: 对于任何一棵二叉树，若度为2的结点数有n2个，则叶子数（n0）必定为n2＋1 （即n0=n2+1）

要理解二叉树中 叶子节点数n₀ = 度为2的节点数n₂ + 1 这个核心性质，关键是从「节点数 」和「边数」的关系入手推导------全程只用到两个基础逻辑，通俗易懂，还能帮你吃透树的本质～

  • 核心逻辑：边数的两种计算方式

    树是「连通无环」的结构，这意味着：边数E和总节点数N有固定关系，同时「边数E也能通过节点的度来计算」------通过这两个角度的等式，就能推导出n₀和n₂的关系。

  • 角度1：从树的结构算边数E

    树没有环，且所有节点连通，所以边数永远比总节点数少1（比如：1个节点→0条边；2个节点→1条边；3个节点→2条边......像一串糖葫芦，节点数比竹签数多1）。

    因此：
    E = N - 1

    代入总节点数N的表达式，得到：
    E = (n₀ + n₁ + n₂) - 1 ------（公式1）

  • 角度2：从节点的度算边数E

    每条边都是「父节点指向子节点」的，所以边数 = 所有节点的子节点总数 （每个子节点对应一条边）。

    而节点的「度」就是子节点个数，因此：

  • 叶子节点（n₀）：度为0 → 贡献0条边；

  • 度为1的节点（n₁）：度为1 → 贡献1条边；

  • 度为2的节点（n₂）：度为2 → 贡献2条边；

总边数E就是所有节点的度之和：
E = 0×n₀ + 1×n₁ + 2×n₂ = n₁ + 2n₂ ------（公式2）

  • 联立等式，推导结论
    因为公式1和公式2都等于边数E，所以联立得：
    (n₀ + n₁ + n₂) - 1 = n₁ + 2n₂

接下来化简方程（一步步来，不跳步）：

  1. 左边展开：n₀ + n₁ + n₂ - 1 = n₁ + 2n₂；
  2. 两边同时减去n₁（等式不变）：n₀ + n₂ - 1 = 2n₂；
  3. 移项整理：n₀ = 2n₂ - n₂ + 1；
  4. 最终得到：n₀ = n₂ + 1。

  • 概念解释：

  • 满二叉树

    一棵深度为k 且有2k -1个结点的二叉树。

    特点：每层都"充满"了结点

  • 完全二叉树
    除最后一层外，每一层上的节点数均达到最大值；在最后一层上只缺少右边的若干结点。

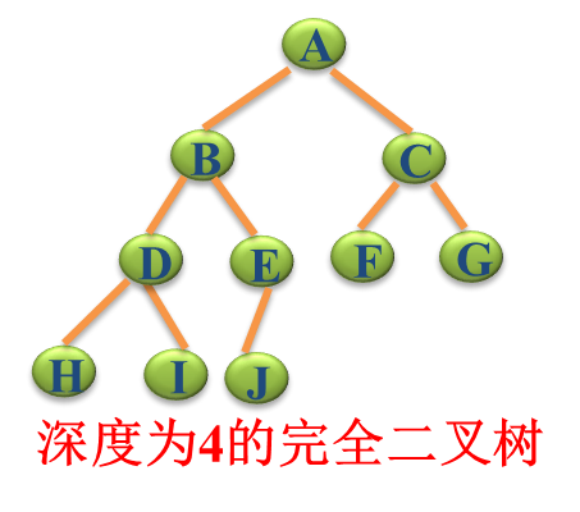
理解：k-1层与满二叉树完全相同，第k层结点尽力靠左

性质4: 具有n个结点的完全二叉树的深度必为 |log2n|+1

性质5: 对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外）

使用此性质可以使用完全二叉树实现树的顺序存储。

如果不是完全二叉树咋整???

------ 将其转换成完全二叉树即可

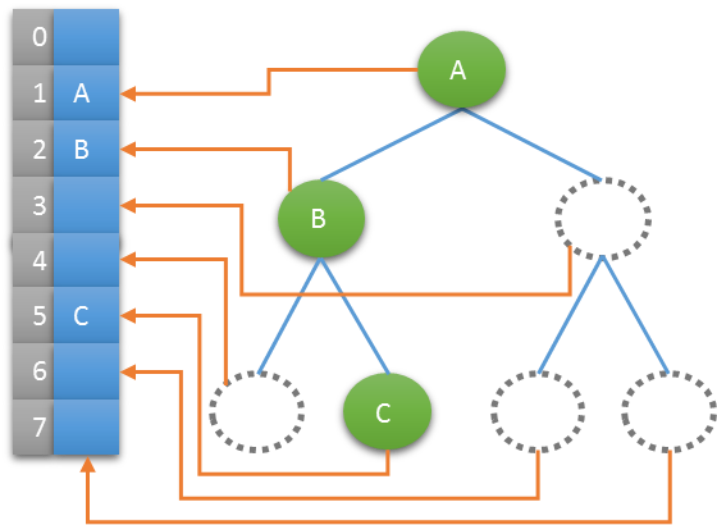
4.3.2二叉树的表示

  • 二叉链表示法

    一般从根结点开始存储。相应地，访问树中结点时也只能从根开始。

  • 存储结构

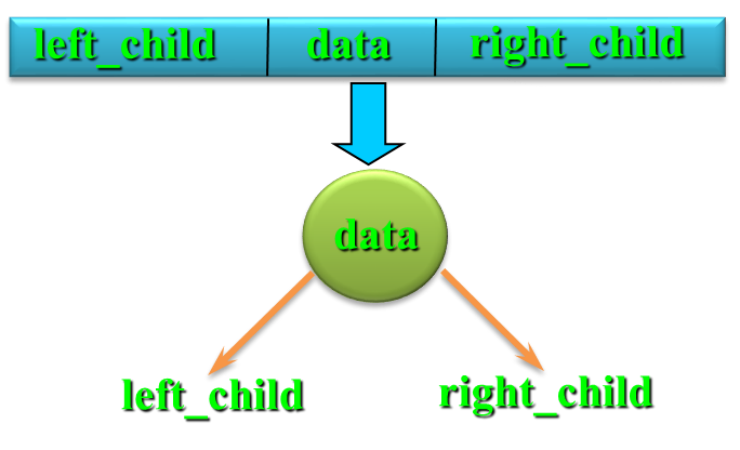
  • 结点数据类型定义：

c 复制代码 
typedef struct BiTNode
{
	int		data;
	struct BiTNode *lchild, *rchild;
}BiTNode, *BiTree;
  • 三叉链表表示法

存储结构

每个节点有三个指针域，其中两个分别指向子节点（左孩子，右孩子），还有一共指针指向该节点的父节点。

节点数据类型定义

c 复制代码 
//三叉链表
typedef struct TriTNode 
{
	int data;
	//左右孩子指针
	struct TriTNode *lchild, *rchild;
	struct TriTNode *parent;
}TriTNode, *TriTree;

4.3.3二叉树的遍历

  • 遍历定义

    指按某条搜索路线遍访每个结点且不重复（又称周游）。

  • 遍历用途

    它是树结构插入、删除、修改、查找和排序运算的前提，是二叉树一切运算的基础和核心。

  • 遍历方法

    牢记一种约定，对每个结点的查看都是"先左后右" 。

    限定先左后右，树的遍历有三种实现方案：

4.3.4二叉树编程实践

4.3.4.1 计算二叉树叶子节点数目

下面提供两种常用的C语言实现方式来计算二叉树的叶子节点数目：

  • 「递归法」（最直观，符合二叉树的递归特性）
  • 「非递归法（层序遍历）」（迭代实现，避免递归栈溢出风险）

代码包含完整的二叉树创建、叶子节点计数、内存释放逻辑，注释清晰，可直接编译运行。

完整代码实现

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 定义二叉树节点结构
typedef struct BiTNode {
    int data;               // 节点数据
    struct BiTNode *lchild; // 左孩子指针
    struct BiTNode *rchild; // 右孩子指针
} BiTNode, *BiTree;

// 队列节点（用于层序遍历）
typedef struct QueueNode {
    BiTree data;            // 存储二叉树节点指针
    struct QueueNode *next;
} QueueNode, *QueuePtr;

// 队列结构（带头节点）
typedef struct {
    QueuePtr front; // 队头
    QueuePtr rear;  // 队尾
} LinkQueue;

/************************ 队列操作（层序遍历用） ************************/
// 初始化队列
void InitQueue(LinkQueue *Q) {
    Q->front = Q->rear = (QueuePtr)malloc(sizeof(QueueNode));
    if (Q->front == NULL) {
        perror("malloc failed");
        exit(1);
    }
    Q->front->next = NULL;
}

// 入队
void EnQueue(LinkQueue *Q, BiTree T) {
    QueuePtr p = (QueuePtr)malloc(sizeof(QueueNode));
    if (p == NULL) {
        perror("malloc failed");
        exit(1);
    }
    p->data = T;
    p->next = NULL;
    Q->rear->next = p;
    Q->rear = p;
}

// 出队（返回队头元素，成功返回1，空队返回0）
int DeQueue(LinkQueue *Q, BiTree *T) {
    if (Q->front == Q->rear) return 0; // 空队
    QueuePtr p = Q->front->next;
    *T = p->data;
    Q->front->next = p->next;
    if (Q->rear == p) Q->rear = Q->front; // 最后一个元素出队
    free(p);
    return 1;
}

// 判断队列是否为空
int QueueIsEmpty(LinkQueue *Q) {
    return Q->front == Q->rear;
}

/************************ 二叉树核心操作 ************************/
/**
 * 递归创建二叉树（用户输入，-1表示空节点）
 * @param T 二叉树根节点的二级指针
 */
void CreateBiTree(BiTree *T) {
    int val;
    printf("请输入节点值（空节点输入-1）：");
    scanf("%d", &val);
    if (val == -1) {
        *T = NULL;
        return;
    }
    *T = (BiTNode *)malloc(sizeof(BiTNode));
    if (*T == NULL) {
        perror("malloc failed");
        exit(1);
    }
    (*T)->data = val;
    CreateBiTree(&(*T)->lchild); // 递归创建左子树
    CreateBiTree(&(*T)->rchild); // 递归创建右子树
}

/**
 * 递归计算叶子节点数（核心逻辑）
 * @param T 当前遍历的节点
 * @return 以T为根的子树的叶子节点数
 */
int CountLeaf_Recursive(BiTree T) {
    if (T == NULL) {
        return 0; // 空树，叶子数为0
    }
    // 叶子节点：左右孩子都为空
    if (T->lchild == NULL && T->rchild == NULL) {
        return 1;
    }
    // 非叶子节点：递归累加左、右子树的叶子数
    return CountLeaf_Recursive(T->lchild) + CountLeaf_Recursive(T->rchild);
}

/**
 * 非递归（层序遍历）计算叶子节点数
 * @param T 二叉树根节点
 * @return 叶子节点总数
 */
int CountLeaf_Iterative(BiTree T) {
    if (T == NULL) return 0; // 空树
    
    LinkQueue Q;
    InitQueue(&Q);
    EnQueue(&Q, T); // 根节点入队
    
    int leafCount = 0;
    BiTree p;
    while (!QueueIsEmpty(&Q)) {
        DeQueue(&Q, &p); // 出队当前节点
        // 判断是否是叶子节点
        if (p->lchild == NULL && p->rchild == NULL) {
            leafCount++;
        }
        // 左孩子非空则入队
        if (p->lchild != NULL) {
            EnQueue(&Q, p->lchild);
        }
        // 右孩子非空则入队
        if (p->rchild != NULL) {
            EnQueue(&Q, p->rchild);
        }
    }
    free(Q.front); // 释放队列头节点
    return leafCount;
}

/**
 * 释放二叉树内存
 * @param T 当前节点
 */
void FreeBiTree(BiTree T) {
    if (T == NULL) return;
    FreeBiTree(T->lchild); // 先释放左子树
    FreeBiTree(T->rchild); // 再释放右子树
    free(T);               // 最后释放当前节点
}

/************************ 主函数（测试） ************************/
int main() {
    BiTree T = NULL;
    
    // 1. 创建二叉树
    printf("===== 开始创建二叉树 =====\n");
    CreateBiTree(&T);
    
    // 2. 递归计算叶子节点数
    int leafRecur = CountLeaf_Recursive(T);
    printf("\n===== 递归法计算结果 =====\n");
    printf("二叉树的叶子节点数：%d\n", leafRecur);
    
    // 3. 非递归（层序）计算叶子节点数
    int leafIter = CountLeaf_Iterative(T);
    printf("\n===== 非递归法（层序遍历）计算结果 =====\n");
    printf("二叉树的叶子节点数：%d\n", leafIter);
    
    // 4. 验证两种方法结果一致
    if (leafRecur == leafIter) {
        printf("\n✅ 两种方法计算结果一致！\n");
    } else {
        printf("\n❌ 两种方法计算结果不一致！\n");
    }
    
    // 5. 释放内存
    FreeBiTree(T);
    T = NULL;
    return 0;
}

核心逻辑说明

1. 递归法（CountLeaf_Recursive）

这是最简洁的实现方式，核心思路：

  • 终止条件：若节点为空（T == NULL），叶子数为0；
  • 叶子节点判断：若节点的左右孩子都为空（T->lchild == NULL && T->rchild == NULL），返回1；
  • 递归递推：非叶子节点的叶子数 = 左子树叶子数 + 右子树叶子数。
2. 非递归法（层序遍历，CountLeaf_Iterative）

适合处理深度较大的二叉树（避免递归栈溢出），核心思路：

  • 利用队列实现层序遍历（从上到下、从左到右遍历所有节点）；
  • 遍历每个节点时，判断是否为叶子节点，若是则计数+1；
  • 非叶子节点的左、右孩子（若有）入队，继续遍历。

测试案例（手把手教你运行）

测试案例1：仅根节点的二叉树

输入流程：

复制代码 
===== 开始创建二叉树 =====
请输入节点值（空节点输入-1）：10
请输入节点值（空节点输入-1）：-1
请输入节点值（空节点输入-1）：-1

输出结果：

复制代码 
===== 递归法计算结果 =====
二叉树的叶子节点数：1

===== 非递归法（层序遍历）计算结果 =====
二叉树的叶子节点数：1

✅ 两种方法计算结果一致！
测试案例2：深度为3的满二叉树

输入流程（节点值：1→2→4→-1→-1→5→-1→-1→3→6→-1→-1→7→-1→-1）：

复制代码 
===== 开始创建二叉树 =====
请输入节点值（空节点输入-1）：1
请输入节点值（空节点输入-1）：2
请输入节点值（空节点输入-1）：4
请输入节点值（空节点输入-1）：-1
请输入节点值（空节点输入-1）：-1
请输入节点值（空节点输入-1）：5
请输入节点值（空节点输入-1）：-1
请输入节点值（空节点输入-1）：-1
请输入节点值（空节点输入-1）：3
请输入节点值（空节点输入-1）：6
请输入节点值（空节点输入-1）：-1
请输入节点值（空节点输入-1）：-1
请输入节点值（空节点输入-1）：7
请输入节点值（空节点输入-1）：-1
请输入节点值（空节点输入-1）：-1

输出结果：

复制代码 
===== 递归法计算结果 =====
二叉树的叶子节点数：4

===== 非递归法（层序遍历）计算结果 =====
二叉树的叶子节点数：4

✅ 两种方法计算结果一致！

注意事项

  1. 输入空节点时必须输入 -1，否则会创建错误的二叉树结构；
  2. 编译命令：gcc binary_tree_leaf.c -o leaf，运行：./leaf；
  3. 非递归法也可改用「栈（深度优先遍历）」实现，逻辑类似（替换队列操作即可）；
  4. 代码中加入了内存释放逻辑（FreeBiTree、队列内存释放），避免内存泄漏。

在代码中，队列的核心作用是支撑「层序遍历（广度优先遍历）」的实现，保证二叉树节点能按「从上到下、从左到右」的顺序被遍历，进而准确统计叶子节点数。

简单来说：队列是层序遍历的「节点管理器」------它用「先进先出（FIFO）」的特性，缓存待处理的二叉树节点，确保遍历顺序符合层序的要求。

一、为什么层序遍历必须用队列？

二叉树的层序遍历要求：先处理当前层 的所有节点，再处理下一层的节点（比如先处理根节点，再处理根的左右孩子，再处理孩子的孩子......）。

这种"先到先处理"的需求，正好匹配队列「先进先出」的特性：

  • 递归/栈（后进先出）：适合「深度优先遍历」（先钻到树的最深处，再回溯）；
  • 队列（先进先出）：适合「广度优先遍历（层序）」（先扫完一层，再扫下一层）。

如果不用队列，无法有序管理"待处理的子节点"，要么会遗漏节点，要么会打乱遍历顺序，导致叶子节点统计错误。

二、队列在代码中的具体使用流程（结合例子）

以「根节点1，左孩子2、右孩子3」的二叉树为例，拆解队列的操作步骤：

步骤 队列状态（队头→队尾） 操作说明
1 [空] 初始化队列，将根节点1入队 → 队列变为 [1]。
2 [1] 出队节点1，判断：1有左右孩子（不是叶子），不计数；将左孩子2、右孩子3入队 → 队列变为 [2,3]。
3 [2,3] 出队节点2，判断：2无左右孩子（是叶子），叶子数+1；无孩子入队 → 队列变为 [3]。
4 [3] 出队节点3，判断：3无左右孩子（是叶子），叶子数+1；无孩子入队 → 队列变为 [空]。
5 [空] 队列为空，遍历结束，最终叶子数=2（符合预期）。

对应代码里的核心逻辑：

c 复制代码 
// 根节点入队（初始化待处理节点）
EnQueue(&Q, T); 
while (!QueueIsEmpty(&Q)) {
    DeQueue(&Q, &p); // 出队"当前待处理节点"
    if (p->lchild == NULL && p->rchild == NULL) {
        leafCount++; // 是叶子则计数
    }
    // 把当前节点的子节点入队（缓存到队列，等待下一轮处理）
    if (p->lchild != NULL) EnQueue(&Q, p->lchild);
    if (p->rchild != NULL) EnQueue(&Q, p->rchild);
}

四、总结队列的核心价值

队列操作 作用
入队（EnQueue） 缓存当前节点的子节点，保证下一层节点按"从左到右"的顺序等待处理。
出队（DeQueue） 取出当前层的待处理节点，完成"叶子节点判断"和"子节点入队"的逻辑。
判空（QueueIsEmpty） 作为层序遍历的终止条件：队列为空 → 所有节点已处理完毕。

简言之，队列是层序遍历的"核心工具"，没有它就无法实现规范的层序遍历，也就无法用非递归的方式按层级统计叶子节点。

版本1：不用栈和队列（纯递归版）

核心：利用函数调用栈（隐式） 遍历，无任何显式栈/队列，代码极简，是统计叶子节点最常用的方式。

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 二叉树节点定义
typedef struct BiTNode {
    int data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
} BiTNode, *BiTree;

/**
 * 递归创建二叉树（-1表示空节点）
 */
void CreateBiTree(BiTree *T) {
    int val;
    printf("输入节点值（空节点输-1）：");
    scanf("%d", &val);
    if (val == -1) {
        *T = NULL;
        return;
    }
    *T = (BiTNode *)malloc(sizeof(BiTNode));
    (*T)->data = val;
    CreateBiTree(&(*T)->lchild); // 递归创建左子树
    CreateBiTree(&(*T)->rchild); // 递归创建右子树
}

/**
 * 纯递归统计叶子节点（无栈/队列）
 * 核心：空节点返回0，叶子节点返回1，非叶子累加左右子树叶子数
 */
int CountLeaf_Recursive(BiTree T) {
    if (T == NULL) return 0;                // 空树，叶子数0
    if (T->lchild == NULL && T->rchild == NULL) return 1; // 叶子节点
    return CountLeaf_Recursive(T->lchild) + CountLeaf_Recursive(T->rchild);
}

/**
 * 释放二叉树内存
 */
void FreeBiTree(BiTree T) {
    if (T == NULL) return;
    FreeBiTree(T->lchild);
    FreeBiTree(T->rchild);
    free(T);
}

int main() {
    BiTree T = NULL;
    printf("===== 创建二叉树 =====\n");
    CreateBiTree(&T);

    int leafNum = CountLeaf_Recursive(T);
    printf("\n二叉树叶子节点数：%d\n", leafNum);

    FreeBiTree(T);
    return 0;
}
测试示例（输入流程）

以二叉树 1→2(-1,-1)→3→4(-1,-1)→5(-1,-1) 为例：

复制代码 
===== 创建二叉树 =====
输入节点值（空节点输-1）：1
输入节点值（空节点输-1）：2
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：3
输入节点值（空节点输-1）：4
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：5
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1

二叉树叶子节点数：3

版本2：仅用栈（非递归版，无队列/递归统计）

核心：显式实现栈结构，用「深度优先遍历」统计叶子节点，无队列、无递归统计逻辑。

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 二叉树节点定义
typedef struct BiTNode {
    int data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
} BiTNode, *BiTree;

// 栈节点定义（仅用于非递归遍历）
typedef struct StackNode {
    BiTree data;       // 存储二叉树节点指针
    struct StackNode *next;
} StackNode, *StackPtr;

// 栈结构（带头节点）
typedef struct {
    StackPtr top; // 栈顶指针
} LinkStack;

/**
 * 栈操作：初始化
 */
void InitStack(LinkStack *S) {
    S->top = (StackPtr)malloc(sizeof(StackNode));
    S->top->next = NULL; // 空栈标记
}

/**
 * 栈操作：判空
 */
int StackIsEmpty(LinkStack *S) {
    return S->top->next == NULL;
}

/**
 * 栈操作：入栈
 */
void Push(LinkStack *S, BiTree T) {
    StackPtr p = (StackPtr)malloc(sizeof(StackNode));
    p->data = T;
    p->next = S->top->next; // 新节点指向原栈顶
    S->top->next = p;       // 栈顶指向新节点
}

/**
 * 栈操作：出栈
 */
int Pop(LinkStack *S, BiTree *T) {
    if (StackIsEmpty(S)) return 0; // 空栈返回失败
    StackPtr p = S->top->next;
    *T = p->data;
    S->top->next = p->next;
    free(p);
    return 1;
}

/**
 * 递归创建二叉树（-1表示空节点）
 */
void CreateBiTree(BiTree *T) {
    int val;
    printf("输入节点值（空节点输-1）：");
    scanf("%d", &val);
    if (val == -1) {
        *T = NULL;
        return;
    }
    *T = (BiTNode *)malloc(sizeof(BiTNode));
    (*T)->data = val;
    CreateBiTree(&(*T)->lchild);
    CreateBiTree(&(*T)->rchild);
}

/**
 * 仅用栈统计叶子节点（非递归，无队列）
 * 核心：栈后进先出，先入右孩子、再入左孩子，保证先序遍历顺序
 */
int CountLeaf_Stack(BiTree T) {
    if (T == NULL) return 0; // 空树直接返回0

    LinkStack S;
    InitStack(&S);
    Push(&S, T); // 根节点入栈

    int leafCount = 0;
    BiTree p;
    while (!StackIsEmpty(&S)) {
        Pop(&S, &p); // 出栈当前节点
        
        // 判断是否是叶子节点
        if (p->lchild == NULL && p->rchild == NULL) {
            leafCount++;
        }

        // 栈后进先出：先入右孩子，再入左孩子 → 出栈先处理左孩子
        if (p->rchild != NULL) Push(&S, p->rchild);
        if (p->lchild != NULL) Push(&S, p->lchild);
    }

    free(S.top); // 释放栈头节点
    return leafCount;
}

/**
 * 释放二叉树内存
 */
void FreeBiTree(BiTree T) {
    if (T == NULL) return;
    FreeBiTree(T->lchild);
    FreeBiTree(T->rchild);
    free(T);
}

int main() {
    BiTree T = NULL;
    printf("===== 创建二叉树 =====\n");
    CreateBiTree(&T);

    int leafNum = CountLeaf_Stack(T);
    printf("\n二叉树叶子节点数：%d\n", leafNum);

    FreeBiTree(T);
    return 0;
}
测试示例（输入流程）

同版本1的二叉树，输入后输出：

复制代码 
===== 创建二叉树 =====
输入节点值（空节点输-1）：1
输入节点值（空节点输-1）：2
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：3
输入节点值（空节点输-1）：4
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：5
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1

二叉树叶子节点数：3

核心区别总结

版本 核心实现 显式数据结构 适用场景
不用栈/队列（递归） 函数调用栈（隐） 无 二叉树深度小，追求代码简洁
仅用栈（非递归） 显式栈 栈 二叉树深度大，避免递归栈溢出

我们以一个具体的二叉树 为例，拆解栈在 CountLeaf_Stack 函数中的完整使用流程，让你直观理解栈的每一步操作和作用。

第一步：确定示例二叉树结构

选择一个简单且有代表性的二叉树（叶子节点为2、4、5，总数3）：

复制代码 
    1        （度为2，非叶子）
   / \
  2   3      （2是叶子；3度为2，非叶子）
     / \
    4   5     （4、5都是叶子）

预期结果：叶子节点数 = 3。

第二步：栈的具体使用流程（逐行拆解）

栈的核心特性是「后进先出（LIFO）」，代码中先入右孩子、再入左孩子，保证出栈时按「根→左→右」的先序遍历顺序处理节点。

以下是每一步的栈状态、操作说明，以及对应代码逻辑：

步骤 栈状态（栈顶 → 栈底） 操作说明 代码对应逻辑
1 [空] 初始化栈，将根节点1入栈 → 栈变为 [1]。 InitStack(&S); Push(&S, T);（T是根节点1）
2 [1] 1. 出栈节点1； 2. 判断：1有左右孩子（非叶子），不计数； 3. 先入右孩子3，再入左孩子2 → 栈变为 [2, 3]（栈顶是2）。 Pop(&S, &p);（p=1） if(p->rchild) Push(3); if(p->lchild) Push(2);
3 [2, 3] 1. 出栈节点2； 2. 判断：2无左右孩子（叶子），leafCount+1（当前=1）； 3. 无孩子入栈 → 栈变为 [3]。 Pop(&S, &p);（p=2） if(2->l/r==NULL) leafCount++
4 [3] 1. 出栈节点3； 2. 判断：3有左右孩子（非叶子），不计数； 3. 先入右孩子5，再入左孩子4 → 栈变为 [4, 5]。 Pop(&S, &p);（p=3） Push(5); Push(4);
5 [4, 5] 1. 出栈节点4； 2. 判断：4无左右孩子（叶子），leafCount+1（当前=2）； 3. 无孩子入栈 → 栈变为 [5]。 Pop(&S, &p);（p=4） leafCount++
6 [5] 1. 出栈节点5； 2. 判断：5无左右孩子（叶子），leafCount+1（当前=3）； 3. 无孩子入栈 → 栈变为 [空]。 Pop(&S, &p);（p=5） leafCount++
7 [空] 栈为空，循环终止，返回leafCount=3（与预期一致）。 while(!StackIsEmpty(&S)) 条件不满足，退出循环；return leafCount;

第三步：关键细节解释

  1. 为什么先入右孩子、再入左孩子？

    栈是「后进先出」，如果先入左孩子、再入右孩子，出栈时会先处理右孩子（顺序变成「根→右→左」），虽然不影响叶子节点统计（只要遍历所有节点即可），但代码中刻意按「根→左→右」的先序遍历顺序处理，是为了和递归遍历的顺序保持一致，逻辑更易理解。

  2. 栈的核心作用（对比队列）

    • 栈的「后进先出」支撑深度优先遍历：先钻到树的最深处（比如1→2→返回→3→4→返回→5），再回溯处理其他节点；
    • 队列的「先进先出」支撑广度优先遍历：先处理完一层（1），再处理下一层（2、3），再处理下一层（4、5）。

  3. 每一步的核心目标

    无论入栈/出栈，最终目的都是「遍历所有节点」，并在遍历到每个节点时判断：是否是叶子节点（左右孩子都为空），若是则计数+1。栈只是实现"遍历所有节点"的工具。

第四步：流程总结

栈在代码中的使用可以概括为「入栈初始化 → 出栈判叶子 → 子节点入栈 → 循环至栈空」：

  1. 根节点入栈，启动遍历；
  2. 循环出栈节点，判断是否为叶子（是则计数）；
  3. 非叶子节点的子节点按「右→左」入栈，保证遍历顺序；
  4. 栈空时，所有节点遍历完毕，返回计数结果。

这个流程的核心是用栈「缓存待处理的子节点」，通过「后进先出」的特性实现深度优先遍历，最终完成叶子节点的统计。

4.3.4.2 计算二叉树高度(深度)

思想：

求根结点左子树高度，根结点右子树高度，比较的子树最大高度，再+1。

若左子树还是树，重复步骤1；若右子树还是树，重复步骤1。

二叉树高度（深度）计算实现

核心思想：递归求解------当前节点的树高 = 左子树高度 和 右子树高度的最大值 + 1（+1是当前节点本身的层级）；空树高度为0（递归终止条件）。

以下提供「纯递归版（核心）」和「非递归版（层序遍历，辅助理解）」两种实现，代码注释清晰，可直接编译运行。

版本1：纯递归版（贴合核心思想，最简）

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 二叉树节点定义
typedef struct BiTNode {
    int data;
    struct BiTNode *lchild; // 左孩子
    struct BiTNode *rchild; // 右孩子
} BiTNode, *BiTree;

/**
 * 递归创建二叉树（-1表示空节点）
 * @param T 二叉树根节点的二级指针
 */
void CreateBiTree(BiTree *T) {
    int val;
    printf("输入节点值（空节点输-1）：");
    scanf("%d", &val);
    if (val == -1) {
        *T = NULL;
        return;
    }
    *T = (BiTNode *)malloc(sizeof(BiTNode));
    (*T)->data = val;
    CreateBiTree(&(*T)->lchild); // 递归创建左子树
    CreateBiTree(&(*T)->rchild); // 递归创建右子树
}

/**
 * 递归计算二叉树高度（核心函数）
 * 逻辑：空树高度0 → 求左右子树高度 → 取最大值+1（当前节点层级）
 * @param T 当前遍历的节点
 * @return 以T为根的子树高度
 */
int GetTreeHeight_Recursive(BiTree T) {
    if (T == NULL) {
        return 0; // 终止条件：空树高度为0
    }
    // 递归求左、右子树高度
    int leftHeight = GetTreeHeight_Recursive(T->lchild);
    int rightHeight = GetTreeHeight_Recursive(T->rchild);
    // 当前节点高度 = 左右子树最大高度 + 1
    return (leftHeight > rightHeight ? leftHeight : rightHeight) + 1;
}

/**
 * 释放二叉树内存（避免内存泄漏）
 */
void FreeBiTree(BiTree T) {
    if (T == NULL) return;
    FreeBiTree(T->lchild); // 先释放左子树
    FreeBiTree(T->rchild); // 再释放右子树
    free(T);               // 最后释放当前节点
}

int main() {
    BiTree T = NULL;
    printf("===== 创建二叉树 =====\n");
    CreateBiTree(&T);

    int height = GetTreeHeight_Recursive(T);
    printf("\n二叉树的高度（深度）：%d\n", height);

    FreeBiTree(T);
    return 0;
}
测试示例（输入流程）

以如下二叉树为例（高度为3）：

复制代码 
    1
   / \
  2   3
     / \
    4   5

输入流程：

复制代码 
===== 创建二叉树 =====
输入节点值（空节点输-1）：1
输入节点值（空节点输-1）：2
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：3
输入节点值（空节点输-1）：4
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：5
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1

二叉树的高度（深度）：3

版本2：非递归版（层序遍历，辅助理解）

若不想用递归，可通过「层序遍历（队列）」统计层数（即树高），核心逻辑：每遍历完一层，层数+1。

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 二叉树节点定义
typedef struct BiTNode {
    int data;
    struct BiTNode *lchild;
    struct BiTNode *rchild;
} BiTNode, *BiTree;

// 队列节点（层序遍历用）
typedef struct QueueNode {
    BiTree data;
    struct QueueNode *next;
} QueueNode, *QueuePtr;

// 队列结构（带头节点）
typedef struct {
    QueuePtr front; // 队头
    QueuePtr rear;  // 队尾
} LinkQueue;

/************************ 队列操作 ************************/
void InitQueue(LinkQueue *Q) {
    Q->front = Q->rear = (QueuePtr)malloc(sizeof(QueueNode));
    Q->front->next = NULL;
}

int QueueIsEmpty(LinkQueue *Q) {
    return Q->front == Q->rear;
}

void EnQueue(LinkQueue *Q, BiTree T) {
    QueuePtr p = (QueuePtr)malloc(sizeof(QueueNode));
    p->data = T;
    p->next = NULL;
    Q->rear->next = p;
    Q->rear = p;
}

int DeQueue(LinkQueue *Q, BiTree *T) {
    if (QueueIsEmpty(Q)) return 0;
    QueuePtr p = Q->front->next;
    *T = p->data;
    Q->front->next = p->next;
    if (Q->rear == p) Q->rear = Q->front;
    free(p);
    return 1;
}

/************************ 二叉树操作 ************************/
void CreateBiTree(BiTree *T) {
    int val;
    printf("输入节点值（空节点输-1）：");
    scanf("%d", &val);
    if (val == -1) {
        *T = NULL;
        return;
    }
    *T = (BiTNode *)malloc(sizeof(BiTNode));
    (*T)->data = val;
    CreateBiTree(&(*T)->lchild);
    CreateBiTree(&(*T)->rchild);
}

/**
 * 非递归（层序）计算二叉树高度
 * 逻辑：统计层数，每遍历完一层则高度+1
 */
int GetTreeHeight_Iterative(BiTree T) {
    if (T == NULL) return 0; // 空树高度0

    LinkQueue Q;
    InitQueue(&Q);
    EnQueue(&Q, T);

    int height = 0; // 树高
    while (!QueueIsEmpty(&Q)) {
        int levelSize = 0; // 记录当前层的节点数
        QueuePtr p = Q->front->next;
        // 统计当前层节点数
        while (p != NULL) {
            levelSize++;
            p = p->next;
        }
        // 遍历当前层所有节点，子节点入队
        for (int i = 0; i < levelSize; i++) {
            DeQueue(&Q, &T);
            if (T->lchild != NULL) EnQueue(&Q, T->lchild);
            if (T->rchild != NULL) EnQueue(&Q, T->rchild);
        }
        height++; // 遍历完一层，高度+1
    }

    free(Q.front);
    return height;
}

void FreeBiTree(BiTree T) {
    if (T == NULL) return;
    FreeBiTree(T->lchild);
    FreeBiTree(T->rchild);
    free(T);
}

int main() {
    BiTree T = NULL;
    printf("===== 创建二叉树 =====\n");
    CreateBiTree(&T);

    int height = GetTreeHeight_Iterative(T);
    printf("\n二叉树的高度（深度）：%d\n", height);

    FreeBiTree(T);
    return 0;
}
测试结果

同递归版，输入相同二叉树后输出：二叉树的高度（深度）：3。

核心逻辑拆解（递归版）

以测试示例的二叉树为例，递归计算过程：

  1. 节点4：左右子树为空 → 高度=0+1=1；
  2. 节点5：左右子树为空 → 高度=0+1=1；
  3. 节点3：左子树高1，右子树高1 → 高度=max(1,1)+1=2；
  4. 节点2：左右子树为空 → 高度=0+1=1；
  5. 节点1：左子树高1，右子树高2 → 高度=max(1,2)+1=3；

最终树高为3，完全符合预期。

关键说明

  1. 递归版是核心，完全贴合"求左右子树高度→取最大值+1"的思想，代码极简且易理解；
  2. 非递归版（层序）适合深度极大的二叉树（避免递归栈溢出），核心是"按层遍历，统计层数"；
  3. 空树高度定义为0，仅根节点的树高度为1（符合二叉树高度的标准定义）。
4.3.4.3 拷贝二叉树

思想：

malloc新结点，

拷贝左子树，拷贝右子树，让新结点连接左子树，右子树。

若左子树还是树，重复步骤1、2；若右子树还是树，重复步骤1、2。

二叉树拷贝实现（递归版，贴合核心思想）

核心逻辑：深度拷贝------对每个节点递归执行「申请新内存→拷贝数据→递归拷贝左/右子树→连接子树」，最终生成与原树结构、数据完全一致的新二叉树（而非简单的指针赋值）。

以下是完整代码，包含「二叉树创建→拷贝→遍历验证→内存释放」全流程，注释清晰，可直接编译运行。

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 二叉树节点定义
typedef struct BiTNode {
    int data;               // 节点数据
    struct BiTNode *lchild; // 左孩子指针
    struct BiTNode *rchild; // 右孩子指针
} BiTNode, *BiTree;

/**
 * 递归创建原二叉树（-1表示空节点）
 * @param T 原树根节点的二级指针
 */
void CreateBiTree(BiTree *T) {
    int val;
    printf("输入节点值（空节点输-1）：");
    scanf("%d", &val);
    if (val == -1) {
        *T = NULL;
        return;
    }
    *T = (BiTNode *)malloc(sizeof(BiTNode));
    if (*T == NULL) {
        perror("malloc failed");
        exit(1);
    }
    (*T)->data = val;
    CreateBiTree(&(*T)->lchild); // 递归创建左子树
    CreateBiTree(&(*T)->rchild); // 递归创建右子树
}

/**
 * 递归拷贝二叉树（核心函数，完全贴合思想）
 * 逻辑：
 * 1. 若原节点为空 → 拷贝节点也为空（终止条件）；
 * 2. 否则malloc新节点，拷贝原节点数据；
 * 3. 递归拷贝原节点的左子树，赋值给新节点的左孩子；
 * 4. 递归拷贝原节点的右子树，赋值给新节点的右孩子；
 * 5. 返回新节点指针。
 * @param T 原树的当前节点
 * @return 拷贝后新树的对应节点
 */
BiTree CopyBiTree(BiTree T) {
    if (T == NULL) {
        return NULL; // 原节点为空，拷贝节点也为空
    }
    // 步骤1：malloc新节点
    BiTree newNode = (BiTNode *)malloc(sizeof(BiTNode));
    if (newNode == NULL) {
        perror("malloc failed");
        exit(1);
    }
    // 拷贝原节点的数据
    newNode->data = T->data;
    
    // 步骤2：递归拷贝左子树，连接到新节点
    newNode->lchild = CopyBiTree(T->lchild);
    // 步骤3：递归拷贝右子树，连接到新节点
    newNode->rchild = CopyBiTree(T->rchild);
    
    // 返回新节点（作为上层节点的左/右孩子）
    return newNode;
}

/**
 * 中序遍历二叉树（验证拷贝结果）
 * 遍历顺序：左子树 → 根节点 → 右子树
 */
void InOrderTraverse(BiTree T) {
    if (T == NULL) {
        return;
    }
    InOrderTraverse(T->lchild);  // 遍历左子树
    printf("%d ", T->data);      // 访问根节点
    InOrderTraverse(T->rchild);  // 遍历右子树
}

/**
 * 释放二叉树内存（避免内存泄漏）
 */
void FreeBiTree(BiTree T) {
    if (T == NULL) {
        return;
    }
    FreeBiTree(T->lchild); // 先释放左子树
    FreeBiTree(T->rchild); // 再释放右子树
    free(T);               // 最后释放当前节点
}

int main() {
    BiTree T_origin = NULL; // 原二叉树
    BiTree T_copy = NULL;   // 拷贝后的二叉树

    // 1. 创建原二叉树
    printf("===== 创建原二叉树 =====\n");
    CreateBiTree(&T_origin);

    // 2. 拷贝二叉树
    T_copy = CopyBiTree(T_origin);

    // 3. 验证拷贝结果（中序遍历对比）
    printf("\n===== 原二叉树的中序遍历结果 =====\n");
    InOrderTraverse(T_origin);
    printf("\n===== 拷贝后二叉树的中序遍历结果 =====\n");
    InOrderTraverse(T_copy);

    // 4. 释放内存（原树和拷贝树都要释放）
    FreeBiTree(T_origin);
    FreeBiTree(T_copy);
    T_origin = NULL;
    T_copy = NULL;

    return 0;
}

核心逻辑拆解（结合示例）

以如下原二叉树为例，拆解拷贝过程：

复制代码 
    1        （原树根节点）
   / \
  2   3
     / \
    4   5
拷贝步骤（递归执行）

  1. 拷贝根节点1：

    • malloc新节点newNode_1，赋值newNode_1->data=1；
    • 递归拷贝左子树（节点2）→ 得到newNode_2，赋值newNode_1->lchild = newNode_2；
    • 递归拷贝右子树（节点3）→ 得到newNode_3，赋值newNode_1->rchild = newNode_3。

  2. 拷贝节点2：

    • malloc新节点newNode_2，赋值newNode_2->data=2；
    • 左子树为空 → newNode_2->lchild=NULL；
    • 右子树为空 → newNode_2->rchild=NULL；
    • 返回newNode_2给上层（节点1的左孩子）。

  3. 拷贝节点3：

    • malloc新节点newNode_3，赋值newNode_3->data=3；
    • 递归拷贝左子树（节点4）→ 得到newNode_4，赋值newNode_3->lchild = newNode_4；
    • 递归拷贝右子树（节点5）→ 得到newNode_5，赋值newNode_3->rchild = newNode_5；
    • 返回newNode_3给上层（节点1的右孩子）。

  4. 拷贝节点4/5：

    • 均为叶子节点，malloc新节点后赋值数据，左右孩子为NULL，返回给上层（节点3的左右孩子）。

最终生成的拷贝树与原树结构、数据完全一致，只是所有节点的内存地址不同（深度拷贝）。

测试示例（输入流程+输出）

输入流程（对应上述示例树）：
复制代码 
===== 创建原二叉树 =====
输入节点值（空节点输-1）：1
输入节点值（空节点输-1）：2
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：3
输入节点值（空节点输-1）：4
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：5
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1
输出结果（验证拷贝成功）：
复制代码 
===== 原二叉树的中序遍历结果 =====
2 1 4 3 5 
===== 拷贝后二叉树的中序遍历结果 =====
2 1 4 3 5

关键注意事项

  1. 深度拷贝 vs 浅拷贝 ：
    • 本代码是「深度拷贝」：每个节点都重新malloc内存，拷贝数据，新树和原树无内存关联；
    • 若直接赋值指针（T_copy = T_origin）是「浅拷贝」，仅共享内存，修改一个树会影响另一个，且释放时会重复释放导致崩溃。
  2. 递归终止条件：原节点为NULL时，拷贝节点也返回NULL，避免空指针操作。
  3. 内存释放：原树和拷贝树的内存需分别释放，否则会造成内存泄漏。
  4. 适用性：递归版适合大多数场景，若二叉树深度极大（如1000层以上），可改用「非递归版（栈）」拷贝（逻辑与递归一致，仅用栈模拟递归过程）。
4.4.4 二叉树的非递归遍历

利用栈容器可以实现二叉树的非递归遍历

首先将每个节点都设置一个标志，默认标志为假，根据节点的的状态进行如下流程。

执行上述流程，可以得到先序遍历的结果，如果想得到其他二叉树遍历结果，修改2.4步骤即可。

实现带标志位的栈式非递归遍历 （该流程对应先序遍历逻辑）。核心是给每个节点加"访问标志"，通过栈的"后进先出"特性控制遍历顺序，以下是完整代码实现：

代码实现（带详细注释）

c 复制代码 
#include <stdio.h>
#include <stdlib.h>

// 1. 定义二叉树节点结构
typedef struct BiTNode {
    int data;               // 节点数据
    struct BiTNode *lchild; // 左孩子指针
    struct BiTNode *rchild; // 右孩子指针
} BiTNode, *BiTree;

// 2. 定义栈元素结构（包含二叉树节点+标志位）
typedef struct StackElem {
    BiTree node;  // 指向二叉树节点
    int flag;     // 标志位：0=未访问（假），1=已准备输出（真）
} StackElem;

// 3. 定义栈的链表结构（用于存储StackElem）
typedef struct StackNode {
    StackElem elem;          // 栈元素
    struct StackNode *next;  // 指向下一个栈节点
} StackNode;

// 4. 栈的管理结构（带头节点）
typedef struct {
    StackNode *top;  // 栈顶指针
} LinkStack;


/************************ 栈的基础操作 ************************/
// 初始化栈
void InitStack(LinkStack *S) {
    S->top = (StackNode *)malloc(sizeof(StackNode));
    if (S->top == NULL) { perror("malloc失败"); exit(1); }
    S->top->next = NULL; // 空栈：栈顶节点的next为NULL
}

// 判断栈是否为空
int StackIsEmpty(LinkStack *S) {
    return S->top->next == NULL;
}

// 入栈（将StackElem压入栈）
void Push(LinkStack *S, StackElem elem) {
    StackNode *newNode = (StackNode *)malloc(sizeof(StackNode));
    if (newNode == NULL) { perror("malloc失败"); exit(1); }
    newNode->elem = elem;       // 存入栈元素
    newNode->next = S->top->next; // 新节点指向原栈顶
    S->top->next = newNode;     // 栈顶指向新节点
}

// 出栈（弹出栈顶元素，存入elem）
int Pop(LinkStack *S, StackElem *elem) {
    if (StackIsEmpty(S)) return 0; // 空栈，出栈失败
    StackNode *p = S->top->next;
    *elem = p->elem;
    S->top->next = p->next;
    free(p);
    return 1;
}


/************************ 二叉树操作 ************************/
// 递归创建二叉树（-1表示空节点）
void CreateBiTree(BiTree *T) {
    int val;
    printf("输入节点值（空节点输-1）：");
    scanf("%d", &val);
    if (val == -1) {
        *T = NULL;
        return;
    }
    *T = (BiTNode *)malloc(sizeof(BiTNode));
    (*T)->data = val;
    CreateBiTree(&(*T)->lchild); // 创建左子树
    CreateBiTree(&(*T)->rchild); // 创建右子树
}

// 按照你的流程实现非递归遍历
void BiTreeNonRecursiveTraverse(BiTree T) {
    if (T == NULL) {
        printf("二叉树为空！\n");
        return;
    }

    LinkStack S;
    InitStack(&S);

    // 步骤1：将根节点压入栈（标志初始为假）
    StackElem rootElem = {T, 0};
    Push(&S, rootElem);

    // 步骤2：栈非空则循环
    while (!StackIsEmpty(&S)) {
        StackElem currElem;
        Pop(&S, &currElem); // 步骤2.1：弹出栈顶元素

        // 步骤2.2：标志为真 → 输出节点
        if (currElem.flag == 1) {
            printf("%d ", currElem.node->data);
            continue; // 直接进入下一次循环
        }

        // 步骤2.3：标志为假 → 设为真
        currElem.flag = 1;

        // 步骤2.4：压入"右子树、左子树、当前节点（已设为真）"
        // 栈是后进先出，因此压入顺序决定弹出顺序：先弹当前节点→再弹左子树→最后弹右子树
        if (currElem.node->rchild != NULL) {
            StackElem rightElem = {currElem.node->rchild, 0};
            Push(&S, rightElem); // 压右子树（标志假）
        }
        if (currElem.node->lchild != NULL) {
            StackElem leftElem = {currElem.node->lchild, 0};
            Push(&S, leftElem);  // 压左子树（标志假）
        }
        Push(&S, currElem);     // 压当前节点（标志真）

        // 步骤2.5：自动进入下一次循环
    }
}

// 释放二叉树内存
void FreeBiTree(BiTree T) {
    if (T == NULL) return;
    FreeBiTree(T->lchild);
    FreeBiTree(T->rchild);
    free(T);
}


/************************ 测试 ************************/
int main() {
    BiTree T = NULL;
    printf("===== 创建二叉树 =====\n");
    CreateBiTree(&T);

    printf("\n===== 非递归遍历结果 =====\n");
    BiTreeNonRecursiveTraverse(T);
    printf("\n");

    FreeBiTree(T);
    return 0;
}

流程对应逻辑（以示例树为例）

以二叉树 1（根）→2（左）、3（右）→3的左4、右5 为例，遍历流程如下：

  1. 根节点1（flag=0）入栈 → 弹出1→设为flag=1→压入3（0）、2（0）、1（1）；
  2. 弹出1（1）→输出1→继续；
  3. 弹出2（0）→设为flag=1→压入（无右/左）→压入2（1）；
  4. 弹出2（1）→输出2→继续；
  5. 弹出3（0）→设为flag=1→压入5（0）、4（0）、3（1）；
  6. 弹出3（1）→输出3→继续；
  7. 弹出4（0）→设为flag=1→压入（无右/左）→压入4（1）；
  8. 弹出4（1）→输出4→继续；
  9. 弹出5（0）→设为flag=1→压入（无右/左）→压入5（1）；
  10. 弹出5（1）→输出5→栈空，遍历结束。

测试结果

输入示例树的创建流程后，输出为：

复制代码 
===== 创建二叉树 =====
输入节点值（空节点输-1）：1
输入节点值（空节点输-1）：2
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：3
输入节点值（空节点输-1）：4
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：5
输入节点值（空节点输-1）：-1
输入节点值（空节点输-1）：-1

===== 非递归遍历结果 =====
1 2 3 4 5

该流程本质是先序遍历（根→左→右），通过栈+标志位实现了递归逻辑的非递归模拟。

5.排序

5.1排序基本概念

现实生活中排序很重要，例如：淘宝按条件搜索的结果展示等。

  • 概念

    排序是计算机内经常进行的一种操作，其目的是将一组"无序"的数据元素调整为"有序"的数据元素。

  • 排序数学定义：

    假设含n个数据元素的序列为{ R1, R2, ..., Rn}，其相应的关键字序列为{ K1, K2, ..., Kn}这些关键字相互之间可以进行比较，即在它们之间存在着这样一个关系 ：

    Kp1≤Kp2≤...≤Kpn

    按此固有关系将上式记录序列重新排列为{ Rp1, Rp2, ...，Rpn}的操作称作排序

  • 排序的稳定性

    如果在序列中有两个数据元素r[i]和r[j]，它们的关键字k[i] == k [j]，且在排序之前，对象r[i]排在r[j]前面。如果在排序之后，对象r[i]仍在r[j]前面，则称这个排序方法是稳定的，否则称这个排序方法是不稳定的。

  • 多关键字排序

    排序时需要比较的关键字多余一个，排序结果首先按关键字1进行排序，当关键字1相同时按关键字2进行排序，当关键字n-1相同时按关键字n进行排序，对于多关键字排序，只需要在比较操作时同时考虑多个关键字即可！

  • 排序中的关键操作

    比较：任意两个数据元素通过比较操作确定先后次序。

    交换：数据元素之间需要交换才能得到预期结果。

  • 内排序和外排序

    内排序：在排序过程中，待排序的所有记录全部都放置在内存中，

    外排序：由于排序的记录个数太多，不能同时放置在内存，整个排序过程需要在内外存之间多次交换数据才能进行。

  • 排序的审判

    时间性能：关键性能差异体现在比较和交换的数量

    辅助存储空间：为完成排序操作需要的额外的存储空间，必要时可以"空间换时间"

    算法的实现复杂性：过于复杂的排序法会影响代码的可读性和可维护性，也可能影响排序的性能

  • 总结

    排序是数据元素从无序到有序的过程

    排序具有稳定性，是选择排序算法的因素之一

    比较和交换是排序的基本操作

    多关键字排序与单关键字排序无本质区别

    排序的时间性能是区分排序算法好坏的主要因素

5.2冒泡排序

一、冒泡排序（Bubble Sort）核心思想

冒泡排序是一种交换排序，核心逻辑是：

  • 重复遍历待排序数组，两两比较相邻元素；
  • 若顺序错误（如升序要求下前数>后数），则交换两者；
  • 每一轮遍历会将当前未排序部分的「最大元素」逐步"冒泡"到末尾；
  • 若某一轮遍历中没有发生任何交换，说明数组已完全有序，可提前终止（优化点）。

二、C语言实现（优化版）

c 复制代码 
#include <stdio.h>

/**
 * 冒泡排序（升序）
 * @param arr 待排序数组
 * @param len 数组长度
 */
void BubbleSort(int arr[], int len) {
    // 1. 外层循环：控制排序轮数（最多 len-1 轮，因为最后1个元素无需比较）
    for (int i = 0; i < len - 1; i++) {
        int isSwapped = 0; // 优化标志：标记本轮是否发生交换（默认无交换）
        
        // 2. 内层循环：每轮比较的次数（已排序的i个元素在末尾，无需比较）
        for (int j = 0; j < len - 1 - i; j++) {
            // 3. 相邻元素比较，升序：前 > 后 则交换
            if (arr[j] > arr[j + 1]) {
                // 交换两个元素
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
                isSwapped = 1; // 标记本轮有交换
            }
        }
        
        // 4. 优化：本轮无交换 → 数组已有序，直接退出
        if (isSwapped == 0) {
            break;
        }
    }
}

// 打印数组
void PrintArray(int arr[], int len) {
    for (int i = 0; i < len; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

int main() {
    // 测试用例
    int arr[] = {5, 2, 9, 1, 5, 6};
    int len = sizeof(arr) / sizeof(arr[0]);

    printf("排序前数组：");
    PrintArray(arr, len);

    // 执行冒泡排序
    BubbleSort(arr, len);

    printf("排序后数组：");
    PrintArray(arr, len);

    return 0;
}
输出结果
复制代码 
排序前数组：5 2 9 1 5 6 
排序后数组：1 2 5 5 6 9

三、算法流程解释（结合示例数组 {5,2,9,1,5,6}）

以示例数组为例，拆解每一轮的比较/交换过程（升序排序）：

轮数(i) 未排序区间 内层比较(j) 比较/交换过程 本轮结果 是否交换
0 [0,5] 0→4 5>2→交换→{2,5,9,1,5,6} 5<9→不换 9>1→交换→{2,5,1,9,5,6} 9>5→交换→{2,5,1,5,9,6} 9>6→交换→{2,5,1,5,6,9} 最大元素9冒泡到末尾 是
1 [0,4] 0→3 2<5→不换 5>1→交换→{2,1,5,5,6,9} 5=5→不换 5<6→不换 次大元素6已在正确位置 是
2 [0,3] 0→2 2>1→交换→{1,2,5,5,6,9} 2<5→不换 5=5→不换 第三大元素5到位 是
3 [0,2] 0→1 1<2→不换 2<5→不换 无交换 否

流程总结：

  1. 第0轮：通过5次比较+4次交换，将最大元素9"冒泡"到数组末尾；
  2. 第1轮：通过4次比较+1次交换，将次大元素6归位；
  3. 第2轮：通过3次比较+1次交换，将5归位；
  4. 第3轮：仅2次比较，无任何交换 → 判定数组已有序，提前终止排序。

四、代码关键逻辑说明

  1. 外层循环（i） ：控制排序轮数，最多执行 len-1 轮（因为每轮至少确定1个元素的位置，最后1个元素无需处理）；
  2. 内层循环（j） ：每轮只比较「未排序区间」的相邻元素，范围是 [0, len-1-i]（已排序的i个元素在末尾，无需比较）；
  3. 交换标志（isSwapped）：若某一轮无交换，说明数组已完全有序，直接退出循环（避免无效遍历，优化时间复杂度）；
  4. 交换逻辑 ：通过临时变量 temp 交换相邻元素，是冒泡排序的核心操作。

五、复杂度分析

指标 最好情况 最坏情况 平均情况 空间复杂度
时间复杂度 O(n) O(n²) O(n²) O(1)
  • 最好情况：数组已完全有序 → 仅1轮遍历（无交换），时间复杂度O(n)；
  • 最坏情况 ：数组完全逆序 → 需执行 len-1 轮，每轮执行 len-1-i 次比较/交换，时间复杂度O(n²)；
  • 空间复杂度：仅使用临时变量（如temp、isSwapped），属于「原地排序」，空间复杂度O(1)；
  • 稳定性：冒泡排序是「稳定排序」（相等元素的相对位置不变，如示例中的两个5）。

六、基础版（无优化）对比

若去掉 isSwapped 优化，基础版冒泡排序代码更简单，但效率更低（即使数组有序，仍会执行 len-1 轮）：

c 复制代码 
void BubbleSort_Basic(int arr[], int len) {
    for (int i = 0; i < len - 1; i++) {
        for (int j = 0; j < len - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                int temp = arr[j];
                arr[j] = arr[j + 1];
                arr[j + 1] = temp;
            }
        }
    }
}

5.3选择排序

一、选择排序（Selection Sort）核心思想

选择排序是一种选择类排序，核心逻辑是：

  • 将数组分为「已排序区间」和「未排序区间」（初始已排序区间为空，未排序区间为整个数组）；
  • 每一轮从「未排序区间」中找到最小元素（升序） ，将其与未排序区间的第一个元素交换；
  • 每轮结束后，已排序区间长度+1，未排序区间长度-1；
  • 重复上述步骤，直到未排序区间为空。

二、C语言实现（升序排序）

c 复制代码 
#include <stdio.h>

/**
 * 选择排序（升序）
 * @param arr 待排序数组
 * @param len 数组长度
 */
void SelectionSort(int arr[], int len) {
    // 1. 外层循环：控制未排序区间的起始位置（i为未排序区间第一个元素下标）
    for (int i = 0; i < len - 1; i++) {
        int minIndex = i; // 初始化：未排序区间第一个元素为"最小值候选"
        
        // 2. 内层循环：遍历未排序区间，找到最小值的下标
        for (int j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {
                minIndex = j; // 更新最小值下标
            }
        }
        
        // 3. 交换：将最小值与未排序区间第一个元素交换
        if (minIndex != i) { // 优化：最小值已在首位则无需交换
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
    }
}

// 打印数组
void PrintArray(int arr[], int len) {
    for (int i = 0; i < len; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

int main() {
    // 测试用例
    int arr[] = {5, 2, 9, 1, 5, 6};
    int len = sizeof(arr) / sizeof(arr[0]);

    printf("排序前数组：");
    PrintArray(arr, len);

    // 执行选择排序
    SelectionSort(arr, len);

    printf("排序后数组：");
    PrintArray(arr, len);

    return 0;
}
输出结果
复制代码 
排序前数组：5 2 9 1 5 6 
排序后数组：1 2 5 5 6 9

三、算法流程解释（结合示例数组 {5,2,9,1,5,6}）

以示例数组为例，拆解每一轮的"找最小值→交换"过程（升序排序）：

轮数(i) 已排序区间 未排序区间 内层遍历(j) 找最小值过程 最小值下标 交换操作 本轮结果
0 [] [0,5] 1→5 初始minIndex=0（值5） j=1（2<5）→minIndex=1 j=2（9>2）→不变 j=3（1<2）→minIndex=3 j=4（5>1）→不变 j=5（6>1）→不变 3（值1） 交换arr[0]和arr[3] {1,2,9,5,5,6}
1 [0] [1,5] 2→5 初始minIndex=1（值2） j=2-5（9/5/5/6均>2）→不变 1（值2） 无需交换 {1,2,9,5,5,6}
2 [0,1] [2,5] 3→5 初始minIndex=2（值9） j=3（5<9）→minIndex=3 j=4（5=5）→不变 j=5（6>5）→不变 3（值5） 交换arr[2]和arr[3] {1,2,5,9,5,6}
3 [0,2] [3,5] 4→5 初始minIndex=3（值9） j=4（5<9）→minIndex=4 j=5（6>5）→不变 4（值5） 交换arr[3]和arr[4] {1,2,5,5,9,6}
4 [0,3] [4,5] 5→5 初始minIndex=4（值9） j=5（6<9）→minIndex=5 5（值6） 交换arr[4]和arr[5] {1,2,5,5,6,9}
5 [0,4] [5] - 未排序区间仅1个元素，无需处理 - - 最终有序数组

流程总结：

  1. 第0轮：从整个数组找到最小值1，交换到数组首位，已排序区间变为[0]；
  2. 第1轮：从未排序区间[1,5]找到最小值2（已在首位），无需交换，已排序区间变为[0,1]；
  3. 第2轮：从未排序区间[2,5]找到最小值5，交换到下标2，已排序区间变为[0,2]；
  4. 第3轮：从未排序区间[3,5]找到最小值5，交换到下标3，已排序区间变为[0,3]；
  5. 第4轮：从未排序区间[4,5]找到最小值6，交换到下标4，已排序区间变为[0,4]；
  6. 第5轮：未排序区间仅1个元素，排序完成。

四、代码关键逻辑说明

  1. 外层循环（i）：

    • 控制未排序区间的起始位置，范围是 [0, len-2]（因为最后1个元素无需比较，必然是最大值）；
    • i 既是未排序区间的第一个元素下标，也是已排序区间的"末尾下一个位置"。

  2. 内层循环（j）：

    • 遍历未排序区间 [i+1, len-1]，目的是找到最小值的下标 minIndex；
    • 初始时 minIndex = i（假设未排序区间第一个元素是最小值），后续通过比较更新。

  3. 交换操作：

    • 只有当 minIndex != i 时才交换（最小值不在未排序区间首位），避免无效交换；
    • 交换后，最小值被放入已排序区间的末尾，未排序区间长度减1。

五、复杂度与稳定性分析

指标 最好情况 最坏情况 平均情况 空间复杂度 稳定性
时间复杂度 O(n²) O(n²) O(n²) O(1) 不稳定
关键说明：

  1. 时间复杂度：

    • 无论数组是否有序，内层循环都要遍历完未排序区间（找最小值），因此最好/最坏/平均时间复杂度均为 O(n²)；
    • 对比冒泡排序：选择排序的交换次数远少于冒泡排序（每轮最多1次交换），因此实际运行效率略高于冒泡排序。

  2. 空间复杂度：

    • 仅使用临时变量（temp、minIndex），属于「原地排序」，空间复杂度 O(1)。

  3. 稳定性：

    • 选择排序是「不稳定排序」（相等元素的相对位置可能改变）；
    • 示例：数组 {5, 2, 9, 1, 5, 6} 中两个5，原顺序是下标0→4，排序后变为下标2→3，相对位置未变（特例）；
    • 反例：数组 {2, 3, 2, 1}，第0轮找到最小值1（下标3），交换arr[0]和arr[3]，结果为 {1, 3, 2, 2}，原下标0的2被交换到下标3，与原下标2的2相对位置改变。

六、降序排序修改

若需实现降序排序，仅需修改内层循环的比较条件：

c 复制代码 
// 降序：找未排序区间的最大值
if (arr[j] > arr[minIndex]) { // 把 < 改为 >
    minIndex = j;
}

5.4插入排序

一、插入排序（Insertion Sort）核心思想

插入排序是一种插入类排序，核心逻辑贴近"整理扑克牌"的过程：

  • 将数组划分为「已排序区间」（初始仅包含第一个元素）和「未排序区间」（剩余所有元素）；
  • 每一轮从「未排序区间」取出第一个元素作为「待插入元素」；
  • 遍历「已排序区间」，找到「待插入元素」的合适位置（保持已排序区间有序）；
  • 将「待插入元素」插入该位置，已排序区间长度+1，未排序区间长度-1；
  • 重复上述步骤，直到未排序区间为空。

二、C语言实现（升序排序）

c 复制代码 
#include <stdio.h>

/**
 * 插入排序（升序）
 * @param arr 待排序数组
 * @param len 数组长度
 */
void InsertionSort(int arr[], int len) {
    // 外层循环：控制未排序区间的起始位置（i是未排序区间第一个元素下标）
    for (int i = 1; i < len; i++) {
        int insertVal = arr[i]; // 保存待插入元素（避免移动时被覆盖）
        int j = i - 1;          // 已排序区间的最后一个元素下标

        // 内层循环：找插入位置 + 移动元素
        // 条件：j≥0（不越界） + 已排序元素 > 待插入元素（升序需后移）
        while (j >= 0 && arr[j] > insertVal) {
            arr[j + 1] = arr[j]; // 已排序元素后移，腾出插入位置
            j--;                 // 向前遍历已排序区间
        }

        // 插入待插入元素到最终位置（j+1是插入下标）
        arr[j + 1] = insertVal;
    }
}

// 打印数组
void PrintArray(int arr[], int len) {
    for (int i = 0; i < len; i++) {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

int main() {
    // 测试用例
    int arr[] = {5, 2, 9, 1, 5, 6};
    int len = sizeof(arr) / sizeof(arr[0]);

    printf("排序前数组：");
    PrintArray(arr, len);

    // 执行插入排序
    InsertionSort(arr, len);

    printf("排序后数组：");
    PrintArray(arr, len);

    return 0;
}
输出结果
复制代码 
排序前数组：5 2 9 1 5 6 
排序后数组：1 2 5 5 6 9

三、算法流程解释（结合示例数组 {5,2,9,1,5,6}）

以示例数组为例，拆解每一轮的"取元素→找位置→插入"过程（升序排序）：

轮数(i) 未排序起始 待插入元素 已排序区间 内层j遍历+元素移动过程 插入位置 本轮结果
1 1 2 [0]（5） j=0 → arr[0]=5>2 → arr[1]=5，j=-1 j+1=0 {2,5,9,1,5,6}
2 2 9 [0,1]（2,5） j=1 → arr[1]=5<9 → 不移动，j=1 j+1=2 {2,5,9,1,5,6}
3 3 1 [0,2]（2,5,9） j=2→arr[2]=9>1→arr[3]=9，j=1 j=1→arr[1]=5>1→arr[2]=5，j=0 j=0→arr[0]=2>1→arr[1]=2，j=-1 j+1=0 {1,2,5,9,5,6}
4 4 5 [0,3]（1,2,5,9） j=3→arr[3]=9>5→arr[4]=9，j=2 j=2→arr[2]=5=5→停止 j+1=3 {1,2,5,5,9,6}
5 5 6 [0,4]（1,2,5,5,9） j=4→arr[4]=9>6→arr[5]=9，j=3 j=3→arr[3]=5<6→停止 j+1=4 {1,2,5,5,6,9}

流程总结：

  1. 第1轮（i=1）：待插入元素2比已排序的5小，5后移，2插入到已排序区间首位；
  2. 第2轮（i=2）：待插入元素9比已排序的5大，直接插入到已排序区间末尾；
  3. 第3轮（i=3）：待插入元素1依次比9、5、2大，这三个元素全部后移，1插入到首位；
  4. 第4轮（i=4）：待插入元素5比9小（9后移），与5相等，插入到同值元素的后面；
  5. 第5轮（i=5）：待插入元素6比9小（9后移），比5大，插入到5和9之间；
  6. 所有元素处理完毕，数组完全有序。

四、代码关键逻辑说明

  1. 外层循环（i）：

    • 从i=1开始（初始已排序区间仅包含arr[0]），遍历到len-1；
    • i是「未排序区间第一个元素」的下标，每轮处理一个未排序元素。

  2. 待插入元素（insertVal）：

    • 提前保存arr[i]的值，避免后续移动元素时覆盖该值（核心细节，否则会丢失数据）。

  3. 内层while循环：

    • j = i-1：从已排序区间的最后一个元素开始向前遍历；
    • 条件j >= 0 && arr[j] > insertVal：保证不越界，且仅当已排序元素大于待插入元素时（升序），才将该元素后移；
    • 元素后移：arr[j+1] = arr[j]，为待插入元素腾出位置。

  4. 插入操作：

    • 最终插入位置是j+1（因为j最后要么是-1，要么是第一个≤待插入元素的下标）；
    • 将insertVal赋值给arr[j+1]，完成插入。

五、复杂度与稳定性分析

指标 最好情况 最坏情况 平均情况 空间复杂度 稳定性
时间复杂度 O(n) O(n²) O(n²) O(1) 稳定
关键说明：

  1. 时间复杂度：

    • 最好情况：数组已完全有序 → 内层while循环每次都不执行，仅外层循环遍历，时间复杂度O(n)；
    • 最坏情况：数组完全逆序 → 每个待插入元素都要遍历整个已排序区间，时间复杂度O(n²)；
    • 平均情况：随机无序数组，时间复杂度O(n²)（但实际效率优于冒泡/选择排序，因为移动元素比交换元素更快）。

  2. 空间复杂度：

    • 仅使用insertVal、j等临时变量，属于「原地排序」，空间复杂度O(1)。

  3. 稳定性：

    • 插入排序是「稳定排序」（相等元素的相对位置不变）；
    • 示例中两个5的原顺序是下标0→4，排序后是下标2→3，相对位置未改变；
    • 核心原因：插入时仅当arr[j] > insertVal才移动元素，相等时停止，保证同值元素的顺序。

六、降序排序修改

若需实现降序排序，仅需修改内层while循环的比较条件：

c 复制代码 
// 降序：已排序元素 < 待插入元素时，才后移
while (j >= 0 && arr[j] < insertVal) {
    arr[j + 1] = arr[j];
    j--;
}
相关推荐
OKkankan1 小时前
多态概念及使用
开发语言·数据结构·c++·算法
lxh01131 小时前
合并K个升序链表题解
前端·数据结构·链表
北冥湖畔的燕雀1 小时前
二叉搜索树：高效查找与删除的实现
数据结构·c++·算法
kupeThinkPoem1 小时前
线段树有哪些算法？
数据结构·算法
小许学java2 小时前
数据结构-包装类和泛型
数据结构·泛型·包装类·java-se
似水এ᭄往昔2 小时前
【C++】--二叉搜索树
开发语言·数据结构·c++
小龙报2 小时前
【算法通关指南：数据结构与算法篇（五）】树的 “自我介绍”：从递归定义到存储绝技（vector vs 链式前向星）
c语言·数据结构·c++·算法·链表·启发式算法·visual studio
报错小能手2 小时前
数据结构 顺序栈
数据结构·算法
风筝在晴天搁浅2 小时前
代码随想录 213.打家劫舍Ⅱ
数据结构
热门推荐
01GitHub 镜像站点02UV安装并设置国内源03安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）04BongoCat - 跨平台键盘猫动画工具05Linux下V2Ray安装配置指南06本地部署阿里最新开源的Z-Image07Meta第三代“分割一切”模型——SAM 3本地部署教程：首支持文本提示分割，400万概念、30毫秒响应，检测分割追踪一网打尽08Gemini 3.0 Pro Preview 实测报告0946个Nano-banana 精选提示词，持续更新中10【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连