【光伏功率预测】EMD 分解 + PCA 降维 + LSTM 的联合建模与 Matlab 实现

1 引言

光伏电站功率输出具有强非线性、强非平稳性与多时间尺度特征：

• 云运动造成秒级/分钟级快速波动；

• 日照与电站温度引入小时/日尺度趋势；

• 季节变化又叠加更长时间尺度的周期性。

传统的单一时间序列模型（如 ARIMA）、简单神经网络（BP、ELM）往往难以同时刻画这些多尺度、非平稳特性。为了更准确地刻画光伏功率的动态过程，本文构建了一个 EMD-PCA-LSTM 联合模型：

先用 EMD（Empirical Mode Decomposition，经验模态分解）将功率序列按时间尺度分解，再用 PCA 对多维分量与外部特征进行降维，最后将降维后的特征序列输入 LSTM 网络进行建模与预测。

本文给出从原理说明 → 特征构造 → Matlab 实现的完整流程，读者可根据自己的数据集直接改造使用。

---

2 模型整体思路与流程

整体流程如下（以 1 步短期预测为例）：

1. 数据准备

   • 收集光伏电站历史出力功率 P(t)

   • 同步获取辐照度 GHI(t)、组件温度 T(t) 等外部特征

   • 按固定时间间隔（如 15 min）重采样、清洗缺失/异常点

2. EMD 分解功率序列

   • 对功率序列 P(t) 进行 EMD：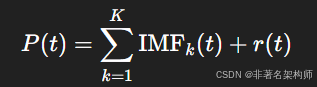

   • 得到若干个 IMF 分量（从高频到低频）与一个剩余项 r(t)

3. 构建特征矩阵 & PCA 降维

   • 将所有 IMF 分量、剩余项，以及外部特征（如 GHI、T）拼成特征矩阵

   • 对特征矩阵进行标准化后，使用 PCA 提取主成分，保留 95% 左右累计方差

   • 获得降维后的特征时间序列 Z(t)

4. 构造 LSTM 训练样本

   • 采用滑动时间窗口，利用前 L 个时刻的主成分序列预测下一个时刻的功率

     • 输入：[Z(t-L+1), ..., Z(t)]

     • 输出：P(t+1)

   • 构造成 Matlab LSTM 所需的序列 cell 数组

5. LSTM 模型训练与预测

   • 定义 LSTM 网络结构：sequenceInputLayer → lstmLayer → fullyConnectedLayer → regressionLayer

   • 使用训练集训练网络

   • 在测试集上进行预测，计算 RMSE、MAE、MAPE 等指标

6. 结果可视化分析

   • 画测试集真实值与预测值对比曲线

   • 统计误差指标，分析模型效果

---

3 关键方法原理简介

3.1 EMD（经验模态分解）

EMD 是一种适用于非线性、非平稳信号的自适应分解方法。它不依赖预设基函数，而是根据数据本身的局部极值自适应地提取一系列本征模态函数 IMF（Intrinsic Mode Functions）。

特点：

• 每个 IMF 基本对应一段频率范围（从高频到低频）

• 对非平稳信号的多尺度成分有清晰分离

• 非参数化，无需先验频率设定

在光伏功率序列中：

• 高频 IMF：往往反映云通过等造成的快速波动

• 中低频 IMF：反映日照变化、功率逐时变化

• 最低频 IMF + 残余：反映日周期/季节趋势

通过 EMD，我们等于是把"难建模的复杂序列"拆成多条相对简单的子序列。

3.2 PCA（主成分分析）

EMD 完成后，我们会得到多条 IMF 分量，再加上 GHI、温度等外部特征，维度往往较高。高维度会带来：

• 模型训练参数变多，容易过拟合

• 维度间存在大量冗余与高度相关性

PCA 通过线性变换将原始特征映射到一组互相正交的主成分上，并按方差大小排序。我们只保留前若干个主成分（累计方差 95% 左右），达到：

• 特征压缩

• 降噪（低方差主成分大多为噪声）

• 加快训练速度

3.3 LSTM（长短期记忆网络）

LSTM 是一种专门为处理长期依赖时间序列设计的循环神经网络结构，通过输入门、遗忘门、输出门控制信息在时间维度上的流动，解决了普通 RNN 的梯度消失问题。

在光伏功率预测中：

• 功率序列在时间上具有明显相关性

• 辐照度和温度等外部特征会在一段时间内持续影响

LSTM 能较好地提取这些时间相关信息。

---

4 数据准备与特征构造

假设我们有一个 CSV 文件 pv_data.csv，包含列：

• time：时间戳（字符串/日期格式）

• P：光伏电站有功出力（kW 或 MW）

• GHI：水平面总辐照度

• Temp：电池板或环境温度

4.1 数据清洗与重采样（概念）

实际工程中建议：

• 对缺失点插值（线性/样条）

• 对异常值进行剔除或替换

• 确保时间间隔固定（例如每 15 分钟一个点）

本文在代码中用简单的线性插值示意。

4.2 EMD 分解的目标序列

本文示例中，我们直接对**历史功率 P(t)**进行 EMD 分解：

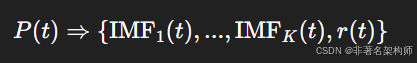
然后将 IMF 分量、残余与外部特征一起作为模型输入的基础特征。

4.3 特征矩阵与 PCA

构造特征矩阵：

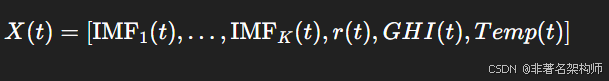
然后进行：

1. 标准化（z-score）

2. PCA 降维，保留前 numPC 个主成分

得到主成分时间序列 Z(t)：

---

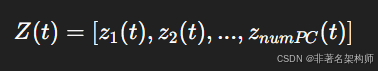
5 Matlab 实现：从数据到预测的完整示例

说明：

• 使用 Matlab Deep Learning Toolbox & Statistics and Machine Learning Toolbox（用于 pca）。

• EMD 使用 Matlab 的 emd 函数（部分版本在信号处理工具箱中，如无可使用 File Exchange 上的 EMD 实现，调用方式类似）。

下面给出一个较完整的 Matlab 脚本示例，可保存为 main_emd_pca_lstm_pv.m 直接运行（根据自己数据微调）。

%% =========================================================================
%  【光伏功率预测】EMD-PCA-LSTM Matlab 实现示例
%  说明：
%    1. 假设数据文件为 pv_data.csv，包含列：time, P, GHI, Temp
%    2. 时间间隔固定（例如 15 分钟）
%    3. 使用 1 步前视预测：用前 L 步特征预测下一步功率
% =========================================================================

clear; clc; close all;

%% ------------------------- 1. 数据读取与预处理 -------------------------
dataFile = 'pv_data.csv';   % 根据实际路径修改
T = readtable(dataFile);

% 假设列名为 'time','P','GHI','Temp'，否则请修改字段名
tRaw  = T.time;
P_raw = T.P;
GHI   = T.GHI;
Temp  = T.Temp;

% 时间格式转换（如果 time 已经是 datetime，可跳过）
if ~isdatetime(tRaw)
    try
        t = datetime(tRaw, 'InputFormat', 'yyyy-MM-dd HH:mm:ss');
    catch
        t = datetime(tRaw); % 尝试自动解析
    end
else
    t = tRaw;
end

% 按时间排序（以防乱序）
[t, sortIdx] = sort(t);
P_raw = P_raw(sortIdx);
GHI   = GHI(sortIdx);
Temp  = Temp(sortIdx);

% 缺失值插值处理
P_raw = fillmissing(P_raw, 'linear');
GHI   = fillmissing(GHI,   'linear');
Temp  = fillmissing(Temp,  'linear');

%% ------------------------- 2. 对功率序列做 EMD -------------------------
% EMD：P_raw -> IMF 分量与残差
% 部分 Matlab 版本 emd 输出 [imf,residual,info]，这里兼容写法：

try
    [imf, residual] = emd(P_raw);       % 常见接口：imf: N x K
catch
    % 如果你的 emd 输出格式不同，可在此处根据函数说明做适配
    error('请确认已安装 EMD 函数并根据实际接口修改此处调用方式。');
end

% 将残余项拼在最后一列
if size(residual, 2) == 1
    X_emd = [imf, residual];
else
    X_emd = [imf, residual(:,1)];
end

[numSamples, numImfPlusRes] = size(X_emd);
fprintf('EMD 分解得到 %d 个 IMF+残差 分量。\n', numImfPlusRes);

%% ------------------------- 3. 构造特征矩阵 + PCA -----------------------
% 特征矩阵：IMF + 残差 + 外部特征(GHI, Temp)
X_full = [X_emd, GHI, Temp];
featureNames = [ ...
    strcat("IMF", string(1:numImfPlusRes-1)), ...
    "Residual", "GHI", "Temp"];

% 同步目标序列（功率）
Y = P_raw(:);

% 剔除 NaN 行（保险起见）
validIdx = all(~isnan(X_full), 2) & ~isnan(Y);
X_full   = X_full(validIdx, :);
Y        = Y(validIdx);
t        = t(validIdx);
[numSamples, numFeatures] = size(X_full);

fprintf('有效样本数: %d, 特征维度: %d\n', numSamples, numFeatures);

% 标准化 X、Y
[X_norm, muX, sigmaX] = zscore(X_full);  % 每列标准化
[Y_norm, muY, sigmaY] = zscore(Y);

% 对标准化后的特征做 PCA
[coeff, score, latent, tsq, explained] = pca(X_norm);

% 选择保留的主成分个数（使累计方差 >= 95%）
cumExplained = cumsum(explained);
numPC = find(cumExplained >= 95, 1, 'first');
if isempty(numPC)
    numPC = size(score, 2); % 兜底：保留全部
end
fprintf('PCA 选择前 %d 个主成分(累计方差 %.2f%%)。\n', ...
    numPC, cumExplained(numPC));

Z = score(:, 1:numPC);  % 主成分时间序列

%% ------------------------- 4. 构造 LSTM 训练样本 ------------------------
% 用前 L 步主成分预测下一步功率
L = 16;   % 时间窗口长度（例如 16*15min=4 小时，可自由调整）

N = size(Z, 1);
numAllSeq = N - L;   % 可构造的样本数
if numAllSeq <= 0
    error('样本数量不足以构造时序窗口，请增加数据长度或减小 L。');
end

XSeq = cell(numAllSeq, 1);
YSeq = cell(numAllSeq, 1);

for i = 1:numAllSeq
    % 时间范围: i ~ i+L-1  -> 输入序列
    % 目标: Y_norm(i+L)
    seqInput = Z(i:i+L-1, :);   % L x numPC
    seqInput = seqInput';       % 转为 numFeatures x L（LSTM 输入要求）
    XSeq{i}  = seqInput;
    
    targetValue = Y_norm(i+L);  % 标准化后的功率
    YSeq{i}    = targetValue;
end

% 划分训练/测试集
trainRatio = 0.7;
numTrain   = floor(numAllSeq * trainRatio);

XTrain = XSeq(1:numTrain);
YTrain = YSeq(1:numTrain);
XTest  = XSeq(numTrain+1:end);
YTest  = YSeq(numTrain+1:end);

tTrainEndIndex = L + numTrain;   % 训练集最后一个样本对应的时间索引
tTest = t(L+1+numTrain : L+numAllSeq); % 测试集对应的时间

%% ------------------------- 5. 搭建并训练 LSTM 网络 ----------------------
numFeaturesLSTM = numPC;
numResponses    = 1;
numHiddenUnits  = 64;  % LSTM 隐含单元数，可调

layers = [ ...
    sequenceInputLayer(numFeaturesLSTM, 'Name', 'input')
    lstmLayer(numHiddenUnits, 'OutputMode', 'last', 'Name', 'lstm')
    fullyConnectedLayer(numResponses, 'Name', 'fc')
    regressionLayer('Name', 'regressionoutput')];

% 训练选项
options = trainingOptions('adam', ...
    'MaxEpochs',       150, ...
    'MiniBatchSize',   64, ...
    'InitialLearnRate',0.005, ...
    'GradientThreshold', 1, ...
    'Shuffle',         'once', ...
    'Plots',           'training-progress', ...
    'Verbose',         false);

fprintf('开始训练 LSTM 网络...\n');
net = trainNetwork(XTrain, YTrain, layers, options);

%% ------------------------- 6. 测试集预测与反标准化 -----------------------
YPred_norm = predict(net, XTest, 'MiniBatchSize', 1);

% 反标准化恢复成原始功率单位
YPred = YPred_norm * sigmaY + muY;

% 将 YTest cell 中的值合并，再反标准化
YTest_norm_vec = cellfun(@(c) c(1), YTest);   % 每个 cell 内是标量
YTest_real = YTest_norm_vec * sigmaY + muY;

%% ------------------------- 7. 误差指标计算与绘图 ------------------------
rmse = sqrt(mean((YPred - YTest_real).^2));
mae  = mean(abs(YPred - YTest_real));
mape = mean(abs((YPred - YTest_real) ./ max(YTest_real, eps))) * 100;

fprintf('测试集 RMSE = %.4f\n', rmse);
fprintf('测试集 MAE  = %.4f\n', mae);
fprintf('测试集 MAPE = %.2f%%\n', mape);

% 绘制真实值 vs 预测值
figure;
plot(tTest, YTest_real, '-','LineWidth',1.2); hold on;
plot(tTest, YPred, '--','LineWidth',1.2);
grid on;
xlabel('Time');
ylabel('PV Power');
legend('真实功率','预测功率');
title('EMD-PCA-LSTM 光伏功率预测结果');

% 误差散点图（真实 vs 预测）
figure;
scatter(YTest_real, YPred, '.');
grid on;
xlabel('真实功率');
ylabel('预测功率');
title('真实值 vs 预测值散点图');
refline(1,0); % y=x 参考线

---

6 代码关键点说明与可选改进

6.1 EMD 调参建议

emd 函数一般提供一些参数（例如最大 IMF 数、插值方式等），可根据数据特性调整：

• MaxNumIMF：控制最大分解阶数，防止过度分解

• Interpolation：极值点插值方法（立方样条等）

• 对于极端不规则数据也可以考虑 EEMD/CEEMDAN，进一步增强鲁棒性

如果发现某些 IMF 看起来像纯噪声，可以考虑舍弃高频 IMF 的一部分，只用中低频 IMF 构造特征。

6.2 PCA 主成分数量的选择

本文代码中通过累计方差达到 95% 自动选取 numPC，实际可做对比：

• 90%、95%、99%... 主成分个数不同对应的预测精度和计算开销

• 若 IMFs 或外部特征本身不多，也可直接不使用 PCA，直接把 IMF + 特征喂进 LSTM

6.3 LSTM 结构与训练策略

可调节的关键超参数包括：

• LSTM 隐含单元数 numHiddenUnits（32、64、128 等）

• 时间窗口长度 L（实际应结合采样间隔和电站惯性来选）

• 学习率 InitialLearnRate

• MaxEpochs、MiniBatchSize 等

可加入 Dropout 或更深层网络：

layers = [ ...
    sequenceInputLayer(numFeaturesLSTM)
    lstmLayer(64,'OutputMode','sequence')
    dropoutLayer(0.2)
    lstmLayer(32,'OutputMode','last')
    fullyConnectedLayer(1)
    regressionLayer];

6.4 多步预测扩展

上文示例为 "用前 L 步预测下一步功率"。如果希望预测未来多步（例如未来 4 个时间点），可以：

• 将 YSeq{i} 扩展为包含多个时刻的向量，网络输出层对应的 numResponses > 1；

• 或采用滚动预测（一次预测一步，再将预测结果反馈回输入）。

---

7 总结

本文构建了一个 EMD-PCA-LSTM 光伏功率预测模型，并给出了可直接运行的 Matlab 代码框架。该模型的核心思想是：

1. EMD 拆解功率序列的多时间尺度成分，增强可建模性；

2. PCA 对多维 IMF + 外部特征进行降维，压缩冗余信息，缓解过拟合；

3. LSTM 建模时间序列长期依赖关系，提取深层动态特征。

在实际工程中，可以继续结合更多输入（如数值天气预报 NWP、历史功率、日类型、节假日标记等）以及更复杂的深度学习结构（如 CNN-LSTM、Attention-LSTM、Transformers 等），在此基础上构建完整的光伏功率预测系统。