26 Clustering 聚类
26.1 What is Clustering
现在开始介绍无监督算法,之前介绍的都是有监督算法,需要用到有标签的训练数据
聚类算法可以自动找到相关或相似的数据点,从无标签的数据中发现数据间的相似特性
26.2 K-means Intuition
- 随机猜测k个簇的中心,簇的中心被称为簇质心(Cluster Centroids)
- 点分配到簇质心:遍历每个样本,每个样本分配到离得更近的簇质心
- 重新计算簇质心:重新计算k类簇的中心,并移动簇质心到中心位置
- 重复2-3步,知道簇质心位置不再变化,点的分配也会不变,这时候K-means聚类算法已经收敛
26.3 K-means Algorithm
现在来看如何实现K-means
定义记号,μk\mu_kμk表示第k个簇质心,x(i)x^{(i)}x(i)表示第i个点,c(i)c^{(i)}c(i)表示第i个点分配的簇质心的编号
- 随机初始化K个聚类中心(簇质心) μ1,μ2,μ3,...,μK\mu_1, \mu_2, \mu_3, ..., \mu_Kμ1,μ2,μ3,...,μK
- 重复点分配和重计算簇质心,伪代码:
Repeat {分配点到簇质心
for i=1 to m
c(i)c^{(i)}c(i) := 离x(i)x^{(i)}x(i)最近的簇质心的编号移动簇质心
for k=1 to K
μk\mu_kμk := 分配到k的点的平均值(每个维度取平均)
}
注:特殊情况,如果某个簇质心没有分配到任何点,那么通常是直接删除该类,或者考虑重新随机初始化,但最常用的做法还是删除该类
26.4 Optimization Objective
为什么K-means算法会收敛?实际上在优化一个成本函数,但是优化方式不是梯度下降
再定义记号:μc(i)\mu_{c^{(i)}}μc(i)表示第i个点分配的簇质心
成本函数/代价函数:
J(c(1),...,c(m),μ1,...,μK)=1m∑i=1m∥x(i)−μc(i)∥2J(c^{(1)}, ..., c^{(m)}, \mu_1, ..., \mu_K) = \frac 1 m \sum_{i = 1}^{m}\|x^{(i)}-\mu_{c^{(i)}}\|^2J(c(1),...,c(m),μ1,...,μK)=m1i=1∑m∥x(i)−μc(i)∥2
注:
- 这里的双竖线即两个向量的距离,这里用的是两个向量之差的L2L_2L2范数,即欧几里得距离
- 介绍一下p-范数(LpL_pLp范数):
∥x⃗∥p=(∣x1∣p+∣x2∣p+...+∣xn∣p)1p\|\vec x\|_p = (|x_1|^p+|x_2|^p+...+|x_n|^p)^{\frac 1 p}∥x ∥p=(∣x1∣p+∣x2∣p+...+∣xn∣p)p1 - 将两个向量作差,算p-范数,即为向量距离。常见的有:
- p=2p=2p=2:欧几里得距离
- $p=1p=1p=1:曼哈顿距离
- p=∞p=\inftyp=∞:切比雪夫距离,此时dCheby(x⃗,y⃗)=maxi(∣xi−yi∣)d_{Cheby}(\vec x, \vec y) = \max_i(|x_i - y_i|)dCheby(x ,y )=maxi(∣xi−yi∣)
回到K-means的成本函数,我们可以发现,K-means中重复的两步实际上是在优化成本函数
第一步点分配到聚类中心,改变c,保持μ不动:
minc(1),...,c(m)J(c(1),...,c(m),μ1,...,μK)\min_{c^{(1)}, ..., c^{(m)}}J(c^{(1)}, ..., c^{(m)}, \mu_1, ..., \mu_K)c(1),...,c(m)minJ(c(1),...,c(m),μ1,...,μK)
第二步移动聚类中心,改变μ,保持c不动:
minμ1,...,μKJ(c(1),...,c(m),μ1,...,μK)\min_{\mu_1, ..., \mu_K}J(c^{(1)}, ..., c^{(m)}, \mu_1, ..., \mu_K)μ1,...,μKminJ(c(1),...,c(m),μ1,...,μK)
注:
- 这个成本函数的名字叫失真函数(Distortion Function)
- 如果某次迭代发现成本函数不再改变,或者减少值小于一个极小值ε\varepsilonε,那么可以停止迭代,认为算法已经收敛
- 这样的优化步骤可以保证收敛到局部最小值,但是不能保证是全局最小值,所以通常我们可以多次随机初始化尝试找到更优的局部最小值,后续章节会介绍
26.5 Initializing K-means
- 选择的K要小于样本数m,否则没有意义
- 通常随机选择K个样本所在的向量位置作为K个初始化的聚类中心,而不是随机取值
- 尝试多次随机初始化并收敛得到最终的成本函数,并选择成本函数最低的,得到更优的局部最优解,这个次数通常在50-1000次之间
26.6 Choosing the Number of Clusters
如何选择聚类的个数呢
首先需要明确一点,由于数据样本是无标签的,所以不存在绝对的正确答案
先介绍ELBO算法:核心思想是绘制横轴是聚类个数,纵轴的最终的失真代价函数的图,找到某个"转折点",这也是ELBO名字的由来(elbow,肘)
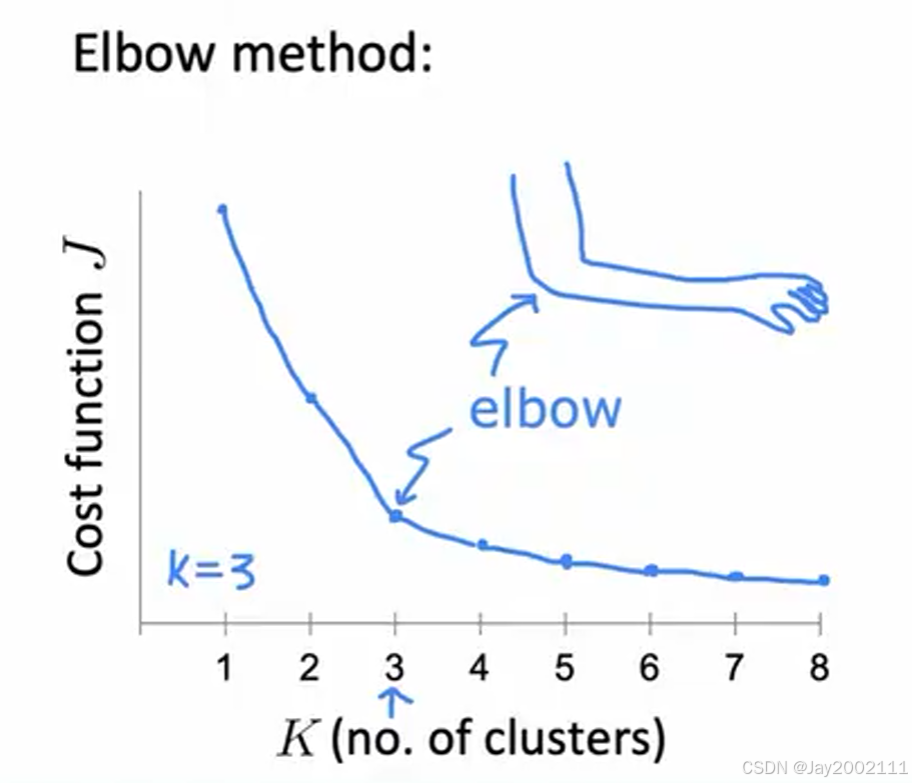
注:
- 最终的成本函数一定会随着K的增大而减小
- 这种方法找到的聚类个数界限不清晰
所以,实际的聚类选择还要结合实际的应用场景
K的增大会造成成本增加,但同时也会使失真代价函数更低,所以K的选择是结合实际场景的权衡选择
例如收集了大量身高腰围等数据,需要聚类选择做衣服的尺码,可以考虑选3个聚类(S M L),5个聚类(XS M L XL XXL)等等,都是合理的,但是要结合实际表现,看增加尺码类型造成的成本增加,和尺码更好地贴合身体数据等因素,进行权衡选择
注:聚类的用途非常广泛,可以用于图像压缩,那么聚类个数的选择要在图像压缩大小和图像清晰程度方面权衡