Title
题目
Unsupervised multimodal surface registration with geometric deep learning
基于几何深度学习的无监督多模态表面配准
01
文献速递介绍
人类大脑皮质是高度回旋折叠的结构,个体间的拓扑结构存在复杂差异(Amunts 等人,2000;Glasser 等人,2016a)。这些差异为皮质表面配准以进行比较分析带来了巨大挑战。 皮质表面配准旨在通过将数据映射到全局平均空间来克服这些挑战,使不同个体大脑组织的共同特征实现重叠。这种配准为各类神经影像分析提供了便利,包括皮质形态测量、功能连接、神经发育及神经外科规划等研究(仅列举部分,Goubran 等人,2019;Risholm 等人,2011;Coalson 等人,2018)。通常,图像匹配以皮质折叠的单变量汇总指标对齐为目标,例如脑沟深度或平均表面曲率(Fischl,2012;Yeo 等人,2009;Robinson 等人,2014);然而,近年来研究发现,皮质折叠难以精确定位某些皮质区域,因此部分框架转而以皮质区域对齐为目标(Nenning 等人,2017;Robinson 等人,2014、2018;Abdollahi 等人,2014)。由于皮质"最优"对齐的定义尚不明确,研究者已开发出多种表面配准算法和技术,涵盖经典优化方法与基于学习的方法(Heinrich 和 Hansen,2020;Dalca 等人,2019),每种方法均采用不同的数学模型、优化算法和相似性度量。 传统上,皮质表面会被映射到球体上,因为球体更能捕捉皮质上点之间的测地线距离。配准过程通过优化目标球体与变形后源球体上特征的相似性度量,并施加平滑性约束来实现。Freesurfer(Fischl 等人,1999)通过优化一组受试者的平均凸度度量与个体凸度度量之间的均方误差(MSE)来配准表面折叠模式,该误差由受试者间凸度的逆方差调制。球形 demons 算法(SD,Yeo 等人,2009)采用由粗到细的方式配准两幅球形图像,它修改了最初在欧几里得图像空间中实现的经典微分同胚 demons 方法(Vercauteren 等人,2009),使用与球面相切的速度向量。多模态表面匹配(MSM,Robinson 等人,2014、2018)同样采用由粗到细的匹配方式,但选择离散优化而非经典方法,因为这在代价函数选择上更具灵活性,且对噪声和局部极小值更稳健。在 MSM 中,通过对变形施加受生物力学启发的超弹性应变正则化,来保证微分同胚特性。研究发现,相较于 Freesurfer、SD 及基于体积的方法,这些特征的组合显著改善了噪声区域特征(静息态功能磁共振成像和 T1w/T2w 髓鞘成像)的对齐效果(Coalson 等人,2018;Glasser 等人,2016b;Robinson 等人,2014、2018;Smith 等人,2013)。 遗憾的是,由于离散优化涉及解决复杂的组合标记问题,其代价是运行时间相对较长(第 4 节)。此外,尽管微分同胚长期以来被视为皮质表面配准的先决条件,但有证据表明,皮质拓扑结构的变异方式可能违背这一假设(Glasser 等人,2016a;Van Essen 和 Glasser,2018)。解决这类问题并非易事,因为要学习如何对齐噪声特征图,同时以合理的方式打破微分同胚约束,首先需要更好地理解变异的潜在来源。因此,一个潜在的解决方案是利用基于学习的图像配准框架(Balakrishnan 等人,2019;Dalca 等人,2019;De Vos 等人,2019;Fan 等人,2018;Heinrich,2019;Pielawski 等人,2020;Shao 等人,2021;Suliman 等人,2022),这些框架已被证明与经典方法精度相当,但效率大幅提升。通过这些框架,对足够多的个体大脑进行配对对齐在计算上成为可能,从而能够映射潜在的变异模式(Guo 等人,2025),或生成基于人口统计学变量或目标表型的群体平均模板(Dalca 等人,2019)。 迄今为止,大多数基于学习的方法集中于体积配准,以现有的经过充分测试且可泛化的卷积架构(如 U-Net,Ronneberger 等人,2015)为基础,学习密集位移场。相比之下,非欧几里得网格域的学习方法尚不成熟,因为其缺乏全局坐标系,导致卷积运算计算效率较低且实现难度更大(Bronstein 等人,2017;Fawaz 等人,2021)。因此,一系列不同的框架应运而生,这些框架通常针对截然不同的非欧几里得域(包括点云(Qi 等人,2017)、流形(Monti 等人,2017)、球体(Zhao 等人,2019)和图(Defferrard 等人,2016))的需求进行定制。尽管如此,仍存在一些值得关注的基于学习的皮质表面配准框架,包括 S3Reg(Zhao 等人,2021)------其通过在球形 U-Net 架构(Zhao 等人,2019)中实现直接邻域(DiNe)卷积来学习位移,并利用微分同胚 Voxelmorph 算法(Dalca 等人,2019)的缩放和平方法来保证微分同胚特性;SUGAR(Ren 等人,2024)------其使用图注意力网络(Velickovic 等人,2017)学习可跨数据集泛化的稳健表面变换;以及 DDR(Suliman 等人,2022)------本文所提框架的早期版本,其在 U-Net 架构中采用 MoNet 卷积(Monti 等人,2017),并通过深度离散配准(Heinrich,2019)进行优化。研究表明,SUGAR 和 DDR 均能学习到比 S3Reg 更平滑、更精确的映射,这很可能是因为与 MoNet(Monti 等人,2017)或图卷积(Velickovic 等人,2017)相比,DiNe 卷积的旋转等变性相对较弱(Zhao 等人,2021;Ren 等人,2024;Suliman 等人,2022)。 所有先前的方法均以皮质折叠的单变量汇总指标(脑沟图和/或曲率)为配准驱动。本文则提出 GeoMorph:一种基于学习的框架,用于多模态皮质区域特征的稳健对齐。由于功能磁共振成像和 T1w/T2w 髓鞘图的噪声水平更高且更稀疏,这一任务难度更大。GeoMorph 再次从 MSM 和 DDR 中汲取灵感,将图像配准构建为深度离散多标签分类问题------在该问题中,低分辨率控制点网格上的点被约束变形到一组固定的目标位置之一,以最大化源(或移动)网格与固定参考网格之间的重叠。然而,它超越了 DDR 中提出的 U-Net 框架,用特征提取网络替代编码器------该特征提取网络为移动特征图和参考特征图分别学习独立的低维表示,以提取特定于每个表面的显著皮质特征。这在处理多通道多模态区域特征时尤为关键,因为每个通道都有其独特的噪声分布和稀疏性挑战。随后,通过使用由循环神经网络(RNN)实现的深度条件随机场(CRF)来施加平滑变形,该网络可推断一阶(成对)正则化惩罚。整个过程以无监督方式进行,即通过优化源特征图和目标特征图的相似性度量(互相关),无需关于期望变换的先验知识。结果表明,尽管与实现了三角团超弹性应变项的 MSMAll 相比,GeoMorph 的成对正则化相对较弱,但在年轻成人人类连接组计划数据集(Glasser 等人,2013、2016a)的区域对齐方面,GeoMorph 表现与 MSM 相当;且其运行时间不到 MSM 的 1/10000,同时能够可靠地泛化到采用截然不同扫描协议采集的未见过的数据(英国生物银行,Alfaro Almagro 等人,2018)。单变量实验和消融研究证实,在单变量对齐方面,GeoMorph 优于 DDR 和 S3Reg,且所有网络组件均对性能提升有贡献。
Aastract
摘要
This paper introduces GeoMorph, a novel geometric deep-learning framework designed for image registrationof cortical surfaces. The registration process consists of two main steps. First, independent feature extraction isperformed on each input surface using graph convolutions, generating low-dimensional feature representationsthat capture important cortical surface characteristics. Subsequently, features are registered in a deep-discretemanner to optimize the overlap of common structures across surfaces by learning displacements of a setof control points. To ensure smooth and biologically plausible deformations, we implement regularizationthrough a deep conditional random field implemented with a recurrent neural network. Experimental resultsdemonstrate that GeoMorph surpasses existing deep-learning methods by achieving improved alignment withsmoother deformations. Furthermore, GeoMorph exhibits competitive performance compared to classicalframeworks. Such versatility and robustness suggest strong potential for various neuroscience applications.
本文提出一种新型几何深度学习框架GeoMorph,专为皮质表面图像配准设计。配准过程包含两个主要步骤:首先,利用图卷积对每个输入表面进行独立特征提取,生成捕捉重要皮质表面特征的低维特征表示;其次,通过深度学习一组控制点的位移,以深度离散方式对特征进行配准,优化不同表面间共同结构的重叠度。为确保变形平滑且符合生物学合理性,我们通过循环神经网络实现的深度条件随机场进行正则化。实验结果表明,GeoMorph通过实现更平滑的变形,配准精度优于现有深度学习方法,且与经典框架相比表现出竞争力。这种多功能性和稳健性使其在各类神经科学应用中具有巨大潜力。
Conclusion
结论
In this paper, we presented GeoMorph, an innovative geometricdeep-learning framework specifically designed for multimodal corticalsurface registration. GeoMorph aims to learn a smooth displacementfield that effectively aligns the features on the moving surface withthose on the target surface. By leveraging independent feature extraction and deep-discrete registration, GeoMorph captures crucial characteristics of cortical surfaces and optimizes feature overlap to achieveimproved alignment. To ensure the generation of visually coherent andanatomically plausible deformations, we incorporate a regularizationnetwork based on a deep conditional random field. Experimental resultsusing sulcal depth features demonstrate that GeoMorph outperformsexisting deep-learning methods by achieving enhanced alignment andgenerating smoother deformations. Moreover, GeoMorph exhibits competitive performance on multimodal alignment, when compared toclassical frameworks, while demonstrating vastly reduced run times.This computational efficiency should prove beneficial for large opendata sets or clinical applications, especially when a pre-existing cortical areal template does not exist; this is particularly important inthe context that multimodal templates capture crucial attribute-relatedtrends, which sets GeoMorph apart from conventional methods thatonly generate templates that capture dominant folding patterns (Dalcaet al., 2019).When comparing the performance of GeoMorph against the deeplearning based method S3Reg (as shown in Table 1), it becomes evidentthat S3Reg exhibits significant high peak distortions. This issue islikely attributed to the hexagonal filter utilized in S3Reg, which lacksrobustness to rotational transformations due to the absence of a globalspherical coordinate system. The solution proposed by S3Reg, whichinvolves a combination of three networks, does not seem to fully overcome this problem, despite efforts to enforce diffeomorphisms throughusing the scaling and squaring approach from the diffeomorphic Voxelmorph algorithm (Dalca et al., 2019). Contrastingly, the GeoMorphstructure does not explicitly enforce diffeomorphisms. Nevertheless,all yielded results are discovered to be diffeomorphic---a foreseeableoutcome due to the strong regularization imposed by the GRF-RNNnetwork.A future expansion of GeoMorph aims to explore relaxing thisrequirement within the framework. The motivation for delving intothis aspect arises from recognizing that achieving perfect alignmenton functional topographies proves unattainable with diffeomorphicallyconstrained deformations. This observation is evident in 10% of subjects for area 55b in Glasser et al. (2016a), as underscored in Schneideret al. (2019). Conventional diffeomorphic registration approaches, asshowcased in Thual et al. (2022), tend to exhibit reduced performance in such scenarios. Finally, it should be highlighted that whileMoNet has empirically demonstrated robustness to rotational transformations (Monti et al., 2017; Fawaz et al., 2021), it lacks formalequivariance guarantees. Future versions of GeoMorph will investigate the integration of theoretically grounded rotationally equivariantconvolution frameworks, such as SE(3)-equivariant networks (Fuchset al., 2020). However, thorough evaluation and additional development will be required, as these networks typically impose a significantcomputational complexity burden.Section 4.2 presents compelling evidence of the advantages offeredby GeoMorphAll in achieving enhanced registration outcomes. Theinclusion of myelin and rfMRI features in the registration process hasproven to be beneficial for individual-to-template alignment. A comparison between GeoMorphAll and MSMAll results, as demonstrated inFigs. 7 and 8 using both HCP and UKB datasets, reveals that GeoMorphAll produces a sharper and clearer average map in the UKB datasetwhen compared to MSMAll. This difference may arise from the factthat MSMAll was originally optimized for the HCP dataset and thatthe feature extraction network in GeoMorph is more advantageous inthe context of the UKB dataset, where the data is considerably noisiercompared to the HCP dataset.The computational complexity of GeoMorph is heavily dependenton the resolution of the control points. As a result, we have been limitedto a control grid on an icosphere of level 4 due to memory constraints.Hence, future extensions of this work will explore more efficient methods to overcome this limitation. Additionally, while the CRF has provento be beneficial in regularizing the deformation field, there is a keeninterest in investigating other regularization techniques that fully leverage the characteristics of the problem. One promising approach is thedevelopment of a mechanically learnable regularization penalty thatconsiders the physical properties of brain tissues. This approach aimsto obtain improved and robust deformations while also allowing fortopology-breaking transformations. Furthermore, it is worth noting thatGeoMorph's implementation is entirely based on MoNet convolutionsthat somewhat limit the expressivity of the features derived fromthe network (Fawaz et al., 2021). Improved performance might beachievable through use of fully expressive, rotation-equivariant surfaceconvolutions such as Cohen et al. (2018) and Wiersma et al. (2020).Alternatively, the incorporation of surface transformer networks, leveraging the attention mechanism as proposed by Dahan et al. (2022),could also lead to improvements by enabling more precise featurealignment through enhanced context awareness and better handling ofcomplex surface variations.
本文提出了GeoMorph,一种专为多模态皮质表面配准设计的创新几何深度学习框架。该框架旨在学习平滑的位移场,实现移动表面与目标表面特征的有效对齐。通过采用独立特征提取与深度离散配准策略,GeoMorph能够捕捉皮质表面关键特征并优化特征重叠度,从而提升配准精度。为确保生成视觉连贯且符合解剖学合理性的变形,框架集成了基于深度条件随机场(CRF)的正则化网络。基于脑沟深度特征的实验结果表明,GeoMorph在配准精度和变形平滑度方面优于现有深度学习方法,且在多模态配准任务中与经典框架表现相当,同时运行时间大幅缩短。这种计算效率优势使其适用于大型开放数据集或临床应用场景,尤其在缺乏预定义皮质区域模板的情况下------多模态模板能够捕捉关键属性相关趋势,这一特性使GeoMorph区别于仅能生成主导折叠模式模板的传统方法(Dalca等人,2019)。 将GeoMorph与深度学习方法S3Reg(表1所示)对比发现,S3Reg存在显著的峰值失真问题。这一现象可能源于S3Reg采用的六边形滤波器:由于缺乏全局球面坐标系,该滤波器对旋转变换鲁棒性不足。尽管S3Reg通过融合三个网络,并借鉴微分同胚Voxelmorph算法(Dalca等人,2019)的缩放和平方法以保证微分同胚特性,但仍未完全解决该问题。相比之下,GeoMorph未明确施加微分同胚约束,但其所有结果均满足微分同胚特性------这一可预期结果得益于GRF-RNN网络施加的强正则化作用。 GeoMorph的未来扩展方向之一是探索在框架中放松微分同胚约束。这一研究动机源于以下观察:在功能拓扑对齐任务中,微分同胚约束下的变形难以实现完美对齐。正如Schneider等人(2019)所强调的,Glasser等人(2016a)的研究显示,10%的受试者在55b脑区存在此类对齐难题。Thual等人(2022)的研究也表明,传统微分同胚配准方法在这类场景中性能会下降。此外,尽管MoNet卷积已通过实证证明对旋转变换具有鲁棒性(Monti等人,2017;Fawaz等人,2021),但其缺乏正式的等变性保证。未来版本的GeoMorph将探索集成理论上可靠的旋转等变卷积框架,例如SE(3)等变网络(Fuchs等人,2020),但由于这类网络通常会带来显著的计算复杂度开销,仍需进一步的评估与开发。 第4.2节提供了充分证据,证明GeoMorphAll在提升配准效果方面的优势。将髓鞘特征和静息态功能磁共振成像(rfMRI)特征纳入配准过程,有助于实现个体到模板的精准对齐。通过HCP和UKB数据集在图7和图8中对GeoMorphAll与MSMAll的结果对比发现,在噪声显著高于HCP数据集的UKB数据集中,GeoMorphAll生成的平均图谱更清晰锐利。这一差异可能源于两方面:一是MSMAll最初是针对HCP数据集优化的;二是GeoMorph的特征提取网络在处理高噪声数据时更具优势。 GeoMorph的计算复杂度很大程度上依赖于控制点的分辨率。受内存限制,当前研究仅采用4级等球面(icosphere level 4)的控制网格,未来工作将探索更高效的方法以突破这一限制。此外,尽管CRF在正则化位移场方面已被证明有效,但仍需研究其他充分利用问题特性的正则化技术。一种具有潜力的方向是开发可学习的力学正则化惩罚项,考虑脑组织的物理特性,以获得更优且稳健的变形,同时允许拓扑破缺变换。值得注意的是,GeoMorph的实现完全基于MoNet卷积,这在一定程度上限制了网络提取特征的表达能力(Fawaz等人,2021)。未来可通过采用完全表达性的旋转等变表面卷积(如Cohen等人,2018;Wiersma等人,2020)提升性能;或者借鉴Dahan等人(2022)的思路,集成表面Transformer网络,利用注意力机制增强上下文感知能力,更好地处理复杂表面变异,从而实现更精确的特征对齐。
Results
结果
4.1. Univariate registration
Fig. 4 illustrates the similarity performances of various runs of allmethods plotted against the 95th percentile of the absolute value ofthe areal distortion. For each similarity level, GeoMorph exhibits distortions falling within the range of the best classical methods (SD andMSM Strain) and demonstrates reduced extremes of areal distortionscompared to S3Reg. Table 1 summarizes the performance of all surfaceregistration frameworks on the task of sulcal depth alignment. In eachcase, results are reported for the configuration that generated a meanCC value of approximately 0.88 (as this is the best CC value thatall methods can achieve). Since the P-values of all methods are veryclose and they are all above the threshold for statistical significance(i.e., 0.05), performance should, therefore, be judged in terms of whichmethods achieve the lowest mean, maximum, 95th percentile, and 98thpercentile values of the distortion. In this, GeoMorph is the second bestperforming framework (behind SD but better than MSM Strain). On theother hand, S3Reg and MSM Pair exhibit much poorer performance. Itis worth noting that these values represent the optimal performance ofS3Reg, across all runs. Moreover, it is worth mentioning that, with theexception of S3Reg, all methods do not have a non-positive Jacobiandeterminant, indicating that they do not produce self-intersecting vertices (i.e., diffeomorphic deformation). In terms of average run time,when utilizing a PC equipped with an NVIDIA Titan RTX 24 GB GPUand an Intel Core i9-9820X 3.30 GHz CPU, GeoMorph exhibits the leastGPU and CPU times among all methods.In Fig. 5, we present histograms showcasing the distribution of bothareal and shape distortions, across all test subjects, at CC of 0.88. Byanalyzing Fig. 5a, we observe that SD and GeoMorph predominantly exhibit areal distortions centered around zero. On the contrary, MSM Pair,S3Reg, and (to a lesser degree) Freesurfer demonstrate pronouncedextreme distortions across subjects, as evidenced by the presence oflong tails in the histogram. This trend is also observable in Fig. 5b,where we observe that the distribution of shape distortions, for SD andGeoMorph, predominantly falls below one. Conversely, other methodsexhibit significant instances of extreme distortions.In Fig. 6, we visually evaluate alignment quality, for all benchmarked methods, on one subject from the HCP dataset that exhibitsatypical cortical folding patterns. Additionally, we examine the arealand shape distortions resulting from these methods. The figure illustrates that GeoMorph, SD, and MSM Strain achieve favorable alignment, with minimal distortions. In contrast, the alignments producedby MSM Pair and S3Reg are characterized by regions with very highdistortions.
4.1 单变量配准 图4展示了所有方法在多轮实验中的相似性表现与区域失真绝对值第95百分位数的关系。在每个相似性水平下,GeoMorph的失真度均处于最佳经典方法(SD和MSM Strain)的范围内,且相较于S3Reg,其区域失真的极端值更小。表1总结了所有表面配准框架在脑沟深度对齐任务中的性能。所有结果均基于均值相关系数(CC)≈0.88的配置(该值为所有方法可达到的最佳相关系数)。由于所有方法的P值非常接近且均高于统计显著性阈值(即0.05),因此性能评估应基于失真度的均值、最大值、第95百分位数和第98百分位数,GeoMorph在这些指标中排名第二(仅次于SD,优于MSM Strain),而S3Reg和MSM Pair的表现则明显较差。值得注意的是,这些数值代表S3Reg在所有实验中的最优性能;此外,除S3Reg外,所有方法的雅可比行列式均非负,表明它们不会产生顶点自交(即满足微分同胚变形特性)。运行时间方面,在配备NVIDIA Titan RTX 24GB GPU和Intel Core i9-9820X 3.30GHz CPU的计算机上,GeoMorph的GPU和CPU运行时间均为所有方法中最短。 图5展示了在相关系数(CC)=0.88时,所有测试受试者的区域失真和形状失真分布直方图。通过分析图5a可知,SD和GeoMorph的区域失真主要集中在零值附近;相反,MSM Pair、S3Reg以及(程度较轻的)Freesurfer在不同受试者中表现出显著的极端失真,直方图中明显存在长尾分布。图5b中形状失真的分布也呈现类似趋势:SD和GeoMorph的形状失真分布主要低于1,而其他方法则存在大量极端失真情况。 图6直观评估了所有基准方法在人类连接组计划(HCP)数据集中一名具有非典型皮质折叠模式的受试者上的对齐质量,并分析了这些方法产生的区域失真和形状失真。结果表明,GeoMorph、SD和MSM Strain实现了良好的对齐效果,失真度极小;而MSM Pair和S3Reg的对齐结果则存在多个高失真区域。
Figure
图
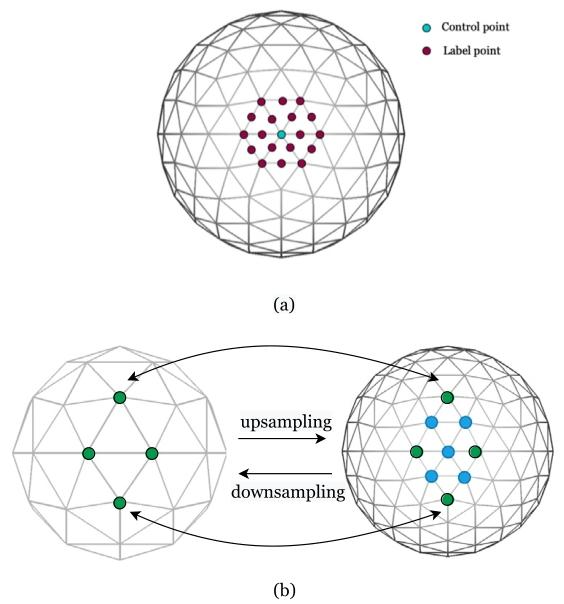
Fig. 1. (a) Example of a control point with its labels on the surface. (b) Upand downsampling on icospheres.
图1 (a) 表面上带标签的控制点示例。(b) 等球面的上采样与下采样过程。
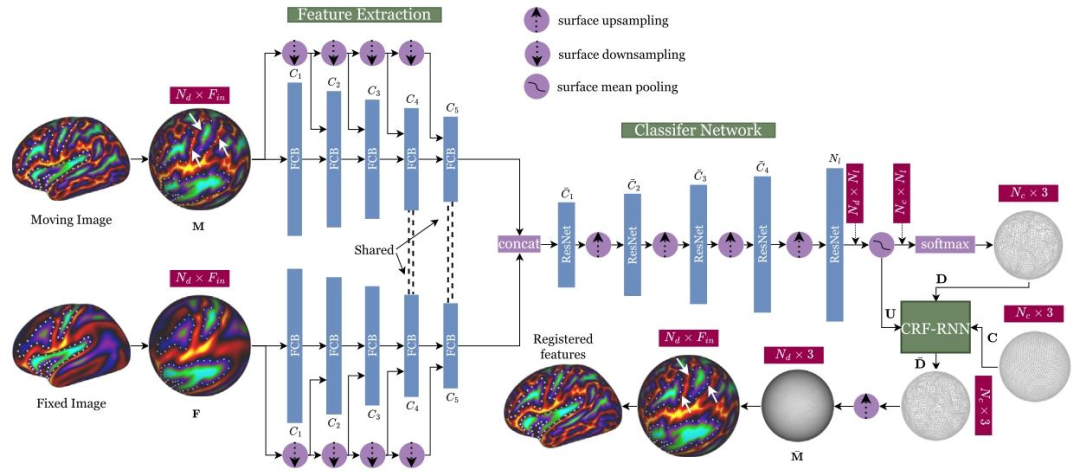
Fig. 2. GeoMorph network architecture. The dimensions in red boxes shows the input and the output dimensions at different network stages. White dots highlightexamples of reference areas within the fixed image, illustrating movements in the brain regions between moving and registered images. White arrows pointingto some areas that have moved the most.
图2 GeoMorph网络架构。红色框内的维度表示网络不同阶段的输入和输出维度。白点突出显示固定图像中的参考区域示例,展示了移动图像与配准后图像之间大脑区域的位移情况。白色箭头指向部分位移最显著的区域。
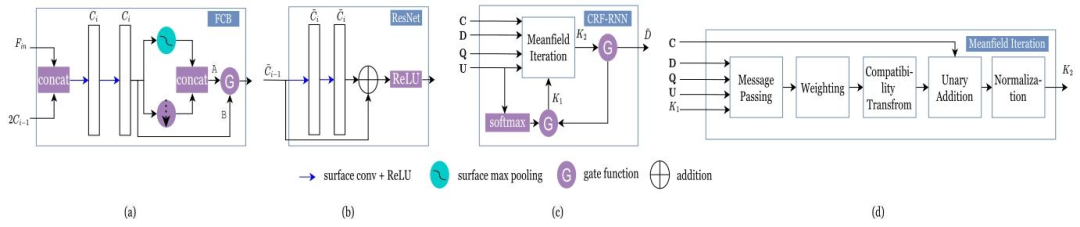
Fig. 3. (a) FCB architecture. (b) ResNet architecture. (c) CRF-RNN architecture. (d) Meafield Iterations architecture
图3 (a) FCB架构。(b) 残差网络(ResNet)架构。(c) 条件随机场-循环神经网络(CRF-RNN)架构。(d) 均值场迭代(Meanfield Iterations)架构。
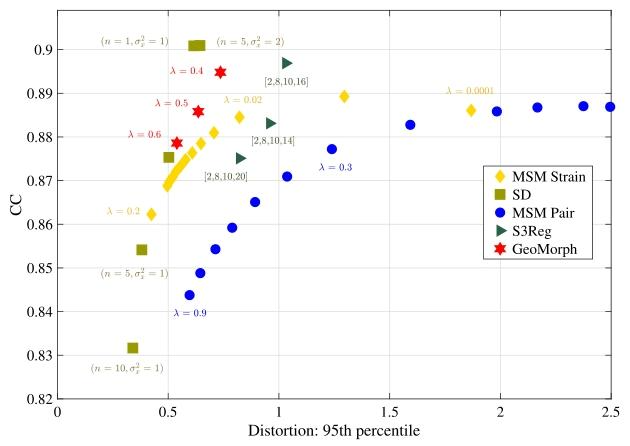
Fig. 4. Similarity performances of all methods vs. the 95th percentile of the areal distortion at multiple regularization levels across runs.
图 4 多轮实验中,不同正则化水平下所有方法的相似性表现与区域失真的第 95 百分位数对比。
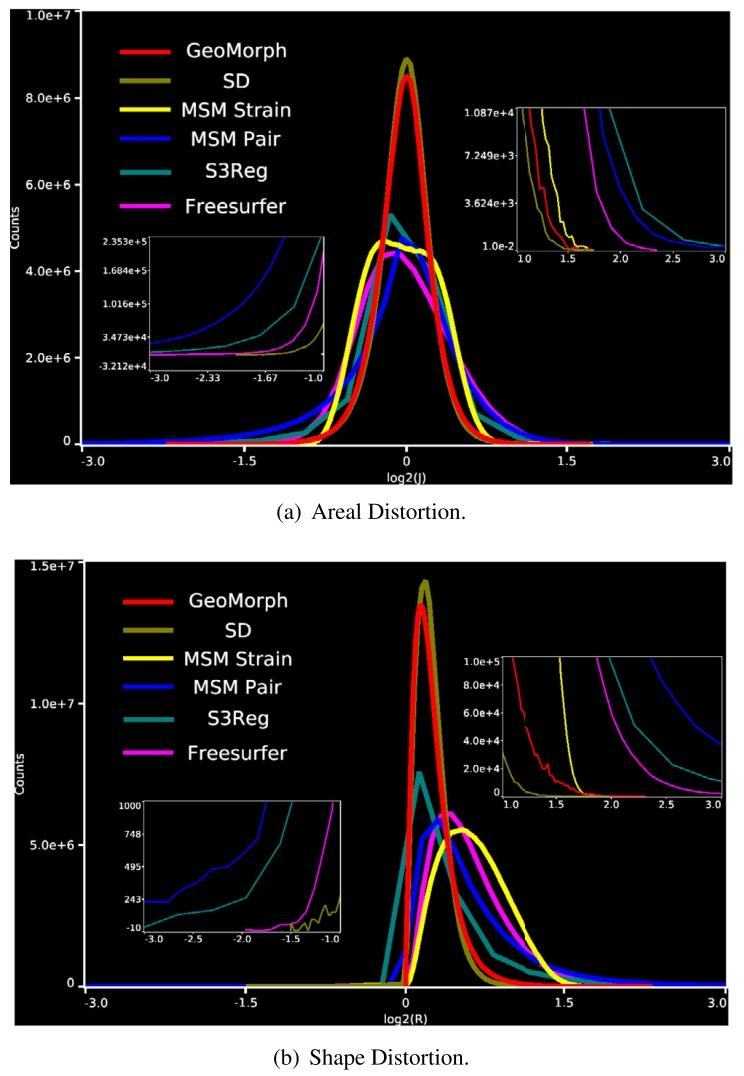
Fig. 5. Histogram plots comparing areal and shape distortions across all test subjects.
图5 所有测试受试者的区域失真与形状失真对比直方图。
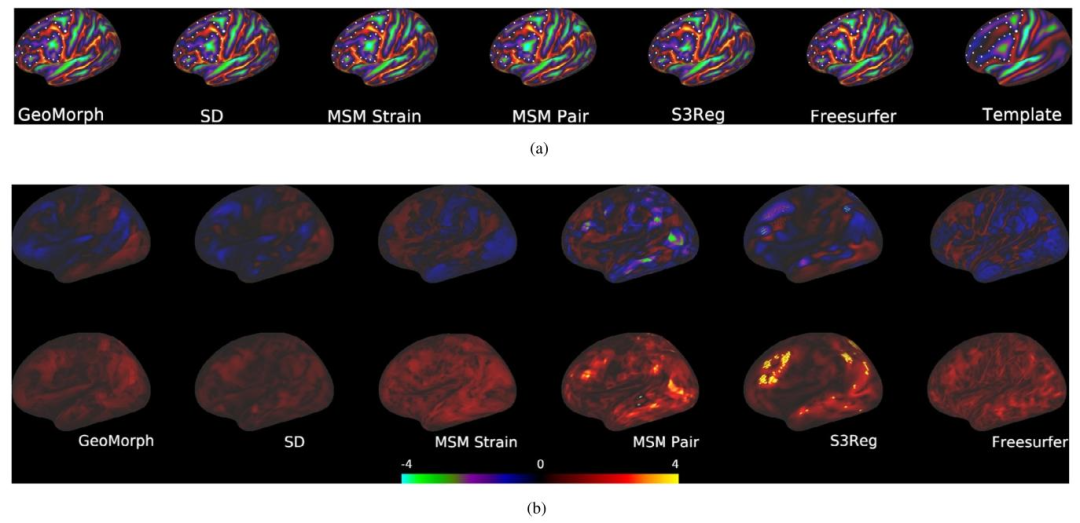
Fig. 6. (a) Registration Performance. (b) Areal (top) and shape (bottom) distortions.
图6 (a) 配准性能。(b) 区域失真(上方)与形状失真(下方)。
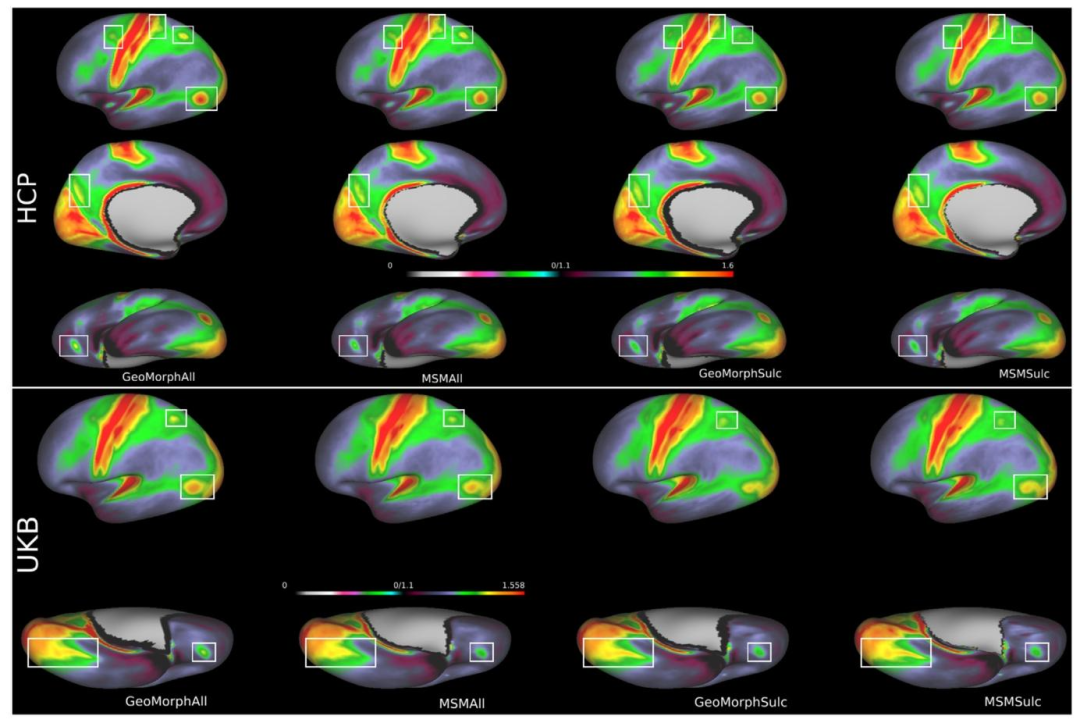
Fig. 7. Intersubject averages of myelin features in HCP (top) and UKB (bottom). Regions in the brain that exhibit significant disparities in contrasts and enhancedperformance between these methods are denoted by the areas highlighted within white boxes.
图7 人类连接组计划(HCP,上方)和英国生物银行(UKB,下方)数据集中髓鞘特征的受试者间平均值。白色框突出显示的区域为大脑中对比度存在显著差异且各方法性能提升明显的区域。
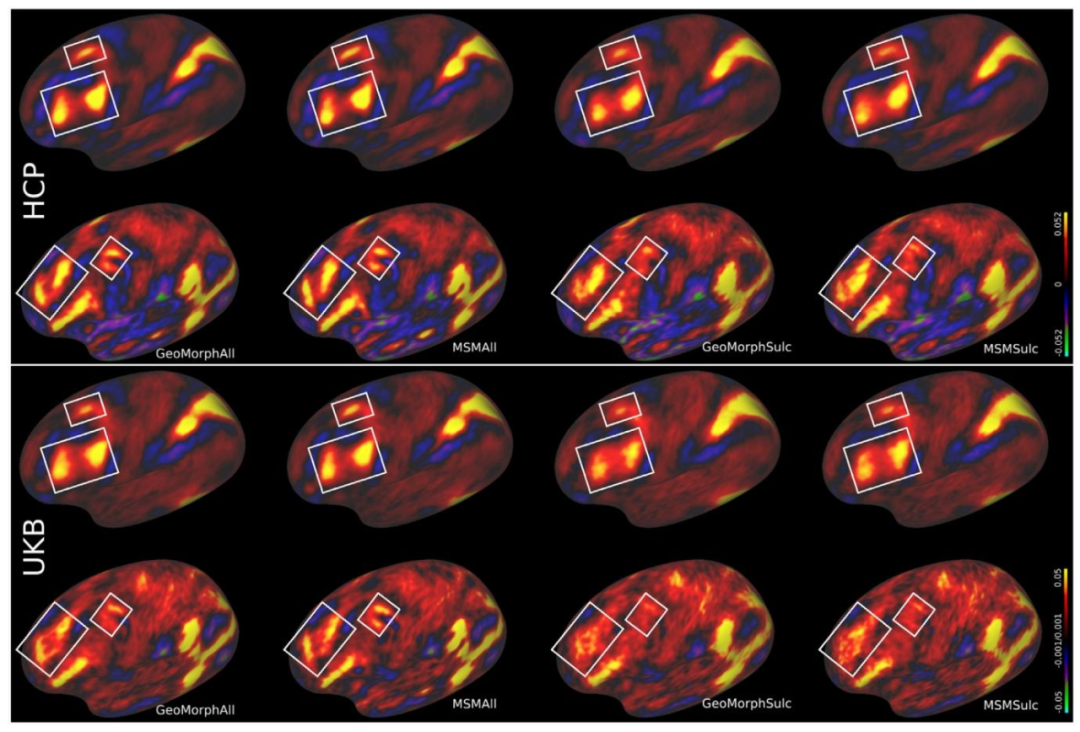
Fig. 8. Intersubject averages of rfMRI features in HCP (top) and UKB (bottom). Regions in the brain that exhibit significant disparities in contrasts and enhancedperformance between these methods are denoted by the areas highlighted within white boxes.
图8人类连接组计划(HCP,上方)和英国生物银行(UKB,下方)数据集中静息态功能磁共振成像(rfMRI)特征的受试者间平均值。白色框突出显示的区域为大脑中对比度存在显著差异且各方法性能提升明显的区域。
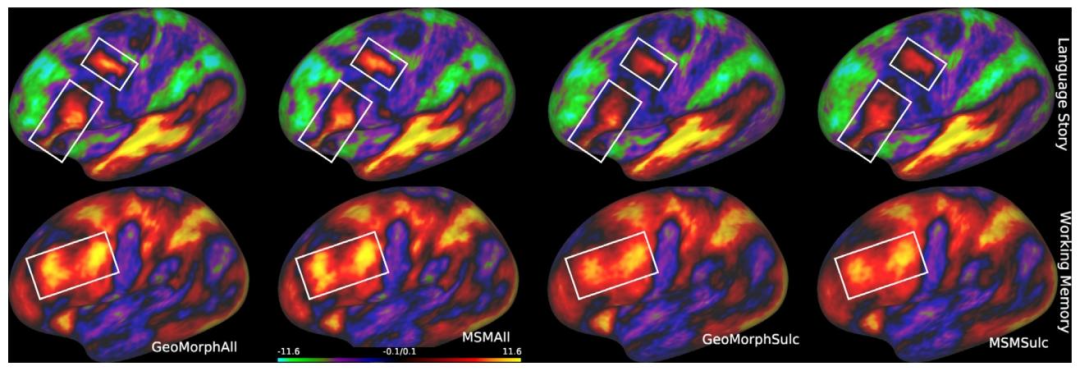
Fig. 9. Comparison of group Z-statistic spatial maps of all methods for (a) Language Story task. (b) Working Memory task. White boxes highlight improvementsin the sharpness of the contrast, with GeoMorphAll and MSMAll maintaining a close comparable performance that outperforms unimodal methods.
图9 所有方法在(a)语言故事任务、(b)工作记忆任务中的组水平Z统计量空间图对比。白色框突出显示对比度锐度的提升效果,其中GeoMorphAll与MSMAll表现接近且优于单模态方法。
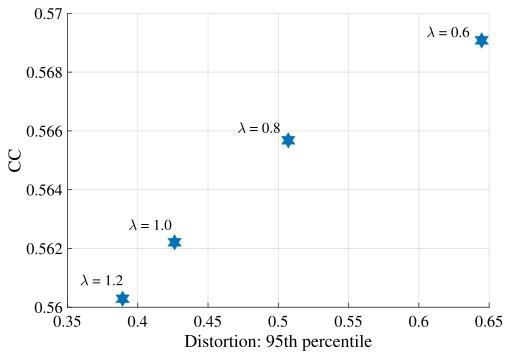
Fig. 10. Similarity performances vs. the 95th percentile of the areal distortionat multiple regularization levels.
图10 不同正则化水平下,相似性表现与区域失真第95百分位数的关系图。
Table
表

Table 1Distortions measures and average runtime for different methods at CC ∼ 0.88. Classical methods (top) and learning-based methods (bottom)
表 1 相关系数(CC)≈0.88 时不同方法的失真度量与平均运行时间(上方为经典方法,下方为基于学习的方法)

Table 2Multimodal registration results: CC, distortions measures, and average runtime for different methods. HCP (top) and UKB (bottom).
表 2 多模态配准结果:不同方法的相关系数(CC)、失真度量及平均运行时间
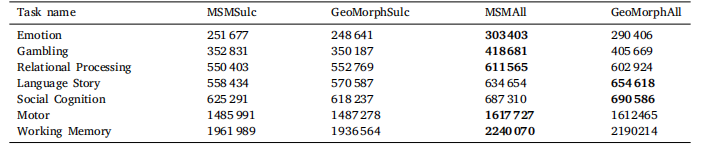
Table 3Cluster mass estimates of the aligned HCP tfMRI data using proposed methods.
表 3 采用所提方法对齐人类连接组计划(HCP)任务态功能磁共振成像(tfMRI)数据后的聚类质量估计结果。
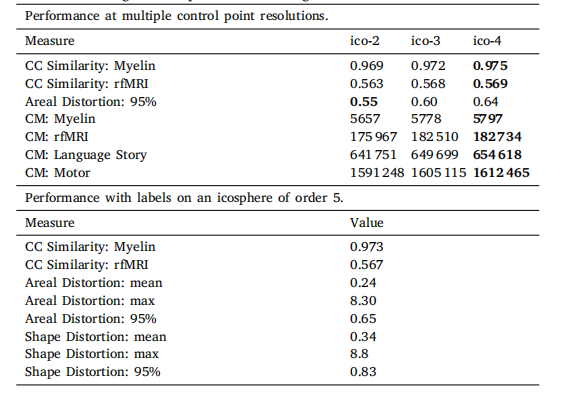
Table 4Results of tuning control point and labels grid resolution
表4 控制点与标签网格分辨率的调优结果
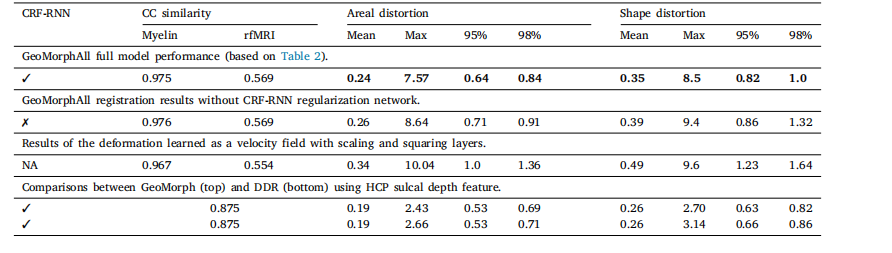
Table 5Ablation experiments using HCP data.
表 5 基于人类连接组计划(HCP)数据集的消融实验结果。

Table 6GeoMorphAll results on UKB
表6 GeoMorphAll在英国生物银行(UKB)数据集上的实验结果。