算法初级教学第三步：链表

第一部分：从内存物理结构看链表------"寻宝游戏"

1. 数组的"局限"与链表的"解放"

回忆一下数组的铁律：必须占用一块连续的内存 。这带来了一个巨大的麻烦："碎片化"问题。

场景： 你的内存还有 1GB 的空闲空间，但是这 1GB 不是连在一起的，而是东一块、西一块，每块只有 1KB 大小。
后果： 如果你想申请一个 2KB 的数组，操作系统会告诉你："内存不足！"（尽管总量足够）。因为数组找不到一块足够大的连续地盘。

链表（Linked List）的诞生，就是为了利用这些破碎的内存空间。 链表对内存说："我不要求连续。随便给我一个小格子就行，但我需要一个机制能把它们串起来。"

2. 节点（Node）：数据与"藏宝图"

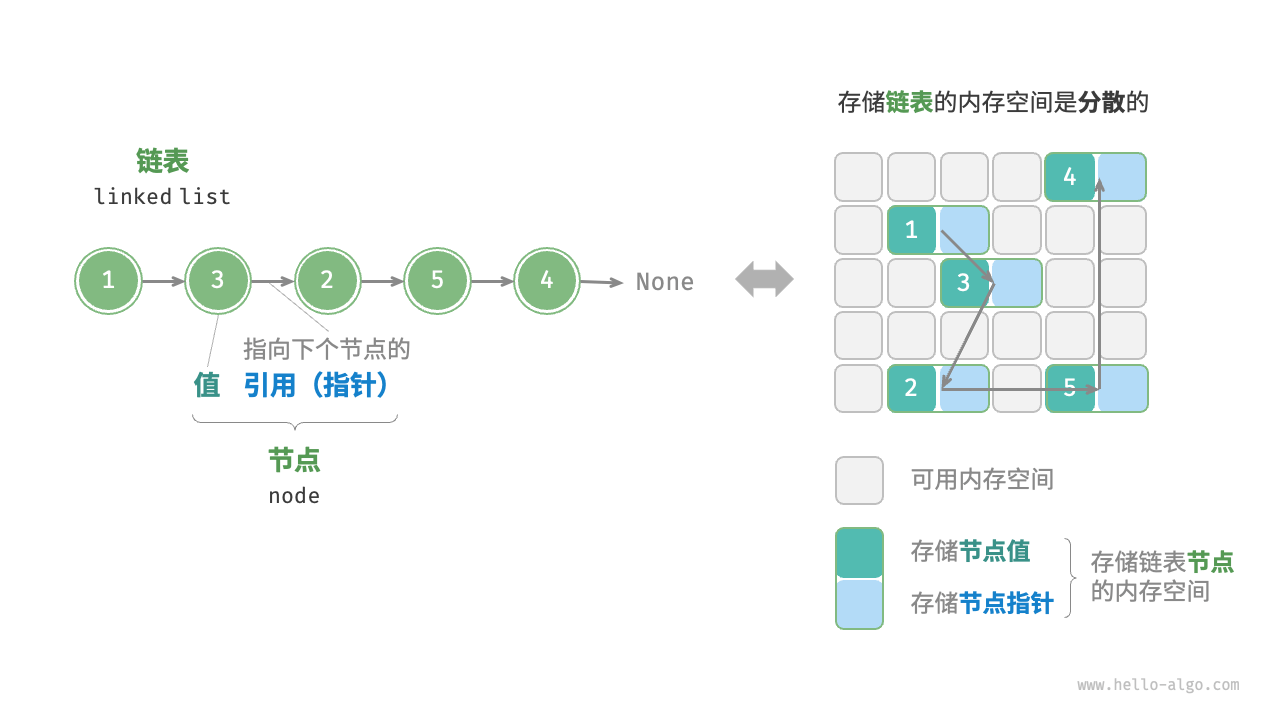
在数组里，只存数据就够了，因为大家挨着住。在链表里，因为大家住得太散，每个元素（我们称为节点 Node）必须携带两样东西：

数据域 (Data)： 真正要存的信息（比如整数 10）。
指针域 (Pointer/Next)： 下一个节点住在哪里（下一个节点的内存地址）。

在计算机底层（比如 C 语言），一个链表节点长这样：

cs 复制代码

struct Node {
    int data;       // 4字节：存数据
    Node* next;     // 8字节(64位系统)：存下一个节点的地址
};

关键点： 你为了存一个 4 字节的整数，不得不额外花费 8 字节来存地址。这就是链表的空间代价。

3. 内存里的真实样子

让我们看看链表在内存街上的布局。假设我们要存 [10, 20, 30]。

不像数组那样整齐排列（100, 104, 108...），链表可能是这样的：

节点	内存实际地址	内部数据 (Data)	内部指针 (Next)	含义
Node A	0xF00	`10`	0x3A0	"我是10，下一个在 0x3A0"
...	...	...	...	(中间隔了很多其他数据)
Node B	0x3A0	`20`	0x888	"我是20，下一个在 0x888"
...	...	...	...	(中间又是十万八千里)
Node C	0x888	`30`	NULL (0x0)	"我是30，后面没人了"

这就像是一个寻宝游戏：

你只拿着第一张字条（头指针 Head），上面写着 0xF00。
你跑到 0xF00，拿到了数据 10，并看到下一条线索：0x3A0。
你跑到 0x3A0，拿到了数据 20，并看到下一条线索：0x888。
你跑到 0x888，拿到了数据 30，发现下一条线索是 0（NULL，空地址），游戏结束。

4. 致命的缺陷：失去"随机访问"能力

还记得数组的公式吗？。

对于链表，这个公式彻底失效了。

如果你想访问链表的第 3 个元素（Node C）：

你不能直接计算出 0x888 这个地址。
你必须先访问 Node A。
读出 A 的 next，找到 Node B。
读出 B 的 next，才能终于找到 Node C。

复杂度对比：

数组访问第 N 个元素： O(1)瞬间到达）。
链表访问第 N 个元素： O(N)（必须顺藤摸瓜，跑断腿）。

这就是为什么在需要频繁查询（Read）的场景下，我们绝不会使用链表。

第一部分总结

从计算机组成原理的第一层看：

物理结构： 链表是离散的内存块，通过指针（地址）强行连接。
空间效率： 它可以利用碎片化内存，但每个节点都有额外的指针开销（存一个 int 甚至可能多浪费 2 倍空间）。
时间效率： 失去了计算地址的能力，查询必须遍历。

第二部分：链表的超能力------内存里的"外科手术"

1. 数组的噩梦：牵一发而动全身

想象一下，你有一个存了 10,000 个整数的数组（紧凑排列），现在你要在第 0 个位置 插入一个新的数字 99。

计算机底层发生了什么？

CPU: "糟糕，第 0 个位置已经被占了。"
搬运工: 为了腾出第 0 个位置，必须把第 0 个数移到第 1 个，第 1 个移到第 2 个......直到第 9999 个移到第 10000 个。
代价: CPU 必须执行 10,000 次写内存（Write）操作。
总结: 这是一个 O(N) 的操作。如果数组有一亿个数据，插入一下电脑可能就卡死一瞬间。

2. 链表的魔法：指针重定向

现在，假设这 10,000 个数据是存在链表里的。

链表节点分散在内存各处，靠指针（地址）手拉手连着。

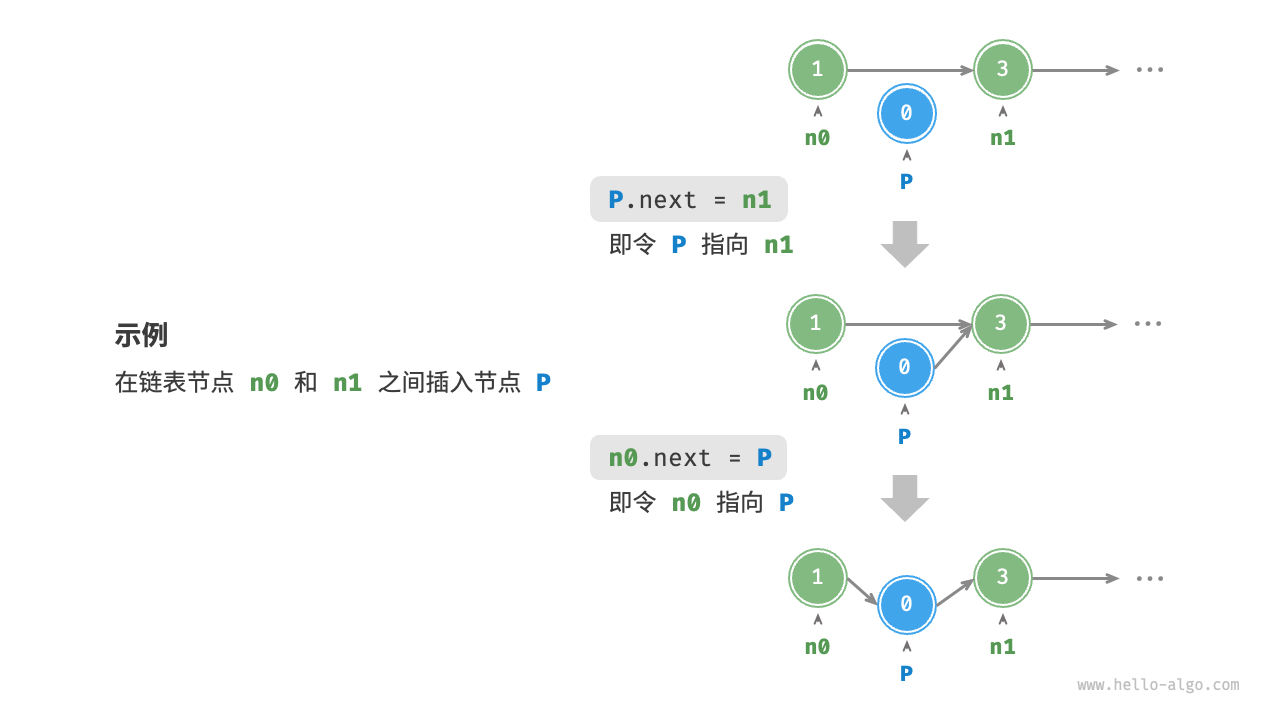
你想在 A 和 B 之间插入一个新节点 New。

计算机底层发生了什么？ 根本不需要挪动 B、C 以及后面几千个节点的位置！它们在内存里纹丝不动。我们要做的仅仅是修改两个地址数据。

手术步骤（非常底层）：

假设：

节点 A 地址：0x100，它的 next 指向 0x200 (节点 B)。
节点 B 地址：0x200。
新节点 New 地址：0x888 (刚刚申请到的)。

步骤 1：让 New 拉住 B 的手

我们将 New 的 next 写入 0x200 (B 的地址)。

(此时：New 指向 B)

步骤 2：让 A 放开 B，改拉 New 的手

我们将 A 的 next 从 0x200 抹去，改写为 0x888 (New 的地址)。

(此时：A 指向 New)

结果：

代价：

不管链表后面有一亿个节点还是三个节点，CPU 只需要做 2 次内存写入。

这就是 O(1)时间复杂度。这是质的飞跃。

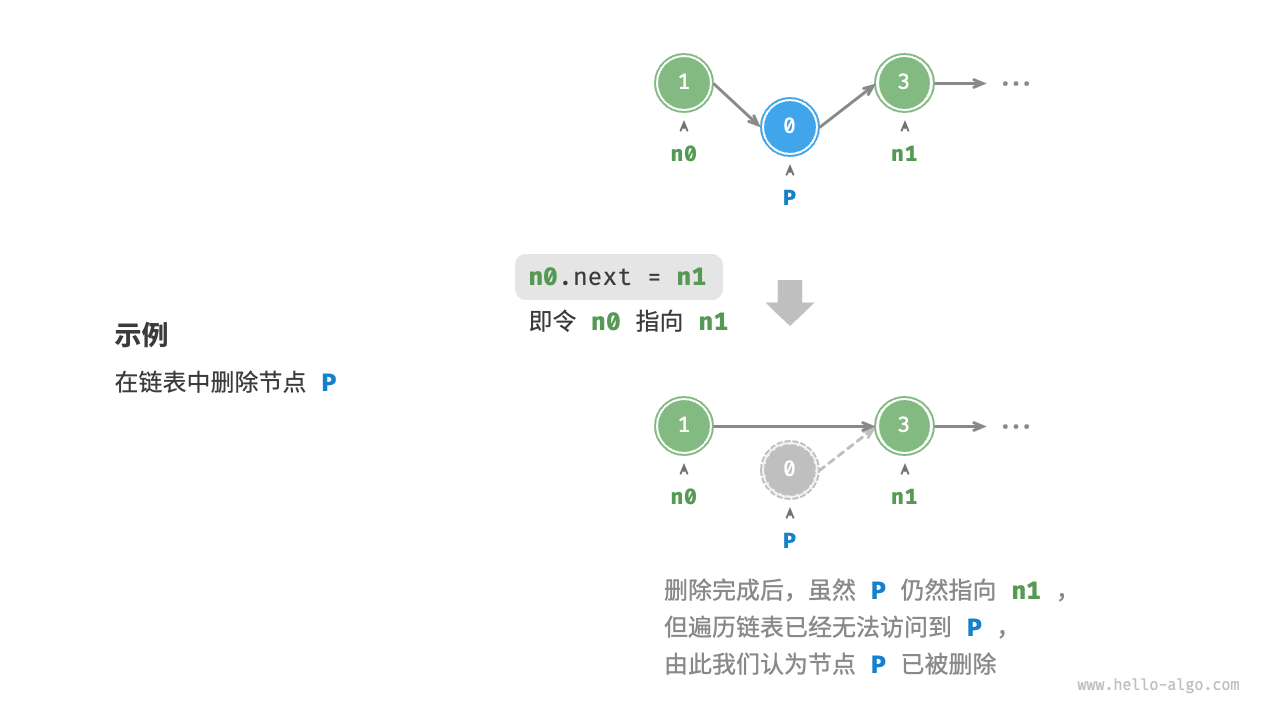
3. 删除操作：过河拆桥

删除节点也是一样的逻辑。

如果要把 B 删掉：

CPU 读取 A 的 next，发现是 B。
CPU 读取 B 的 next，发现是 C。
手术开始：直接把 A 的 next 改写成 C 的地址。
释放内存： 现在的 B 就像断了线的风筝，没有节点指向它了。我们调用 free() 把 B 占用的内存还给操作系统。

注意： 这里的 B 和 C 在物理内存上完全不需要移动，我们只是改变了 A 的"寻宝线索"。

4. 一个残酷的现实细节（新手常忽略）

你可能会问："既然链表插入是 O(1)，为什么我写代码时没那么快？"

这里有一个经典的计算机原理陷阱。

虽然"插入"这个动作本身（改指针）是 O(1) 的，但是找到插入位置这个过程却是 O(N) 的！

如果你想在"第 5000 个节点后面"插入：
1. 你得先从头遍历 5000 次，找到第 5000 个节点（耗时 O(N)）。
2. 然后再做 O(1) 的指针修改。
- 总耗时： 依然是 O(N)。
真正的优势场景：

如果你已经手里攥着第 5000 个节点的地址（比如你在遍历的过程中，或者你有一个指针直接指向它），那么这时候做插入，才是真正的神速。

第二部分总结

从底层操作来看：

数组： 修改结构需要物理搬移数据，代价极高（搬家）。
链表： 修改结构只需要修改指针数值，代价极低（改户口本）。
本质： 链表通过增加"指针"这个维度的复杂性，换取了"拓扑结构"的极度灵活。

下一步 到现在，链表看起来互有胜负。但在现代高性能计算（High Performance Computing）中，链表其实是非常不受待见的。为什么？因为它违反了 CPU 的"天性"。

第三部分：链表 vs CPU 缓存------为什么链表是现代 CPU 的毒药？

1. CPU 的"饥饿游戏"

首先，你要知道 CPU 跑得非常快，而内存（RAM）相对来说非常慢。如果把 CPU 执行一条指令的时间比作 1 秒 ，那么从内存读取一次数据大约需要 200~300 秒。

这意味着，如果 CPU 每次都要伸手去问内存要数据，CPU 大部分时间都在发呆（Stall），等着数据送过来。这简直是巨大的算力浪费。

2. 缓存行 (Cache Line)

为了解决这个问题，CPU 引入了多级缓存（L1, L2, L3 Cache）。最关键的机制叫做 Cache Line（缓存行）。

当 CPU 想要从内存地址 0x1000 读取 1个字节 时，内存控制器并不是只发给它 1 个字节。内存会非常豪爽地把从 0x1000 到 0x103F 的 64 个字节（整整一块）一次性打包发给 CPU。

CPU 心想："既然你读了 0x1000，那你大概率马上就要读 0x1001、0x1002 了吧？我先帮你把这一整块都拿进缓存存着。"

这叫做 "空间局部性原理" (Spatial Locality)。

3. 数组的胜利：顺风车

现在我们来看看数组是怎么利用这个机制的。

场景： 你遍历一个 int 数组。
过程：
1. 当你访问 arr[0] 时，CPU 把 arr[0] 以及后面的 arr[1] 到 arr[15] 全部打包加载到了 L1 缓存里。
2. 当你接下来要访问 arr[1] 时，CPU 发现："嘿！这东西已经在我的 L1 缓存里了！"
3. 耗时： 只需要 0.5纳秒（甚至更短）。

这叫做 Cache Hit（缓存命中）。在数组遍历中，命中率极高，CPU 几乎全速奔跑。

4. 链表的灾难：指针追逐 (Pointer Chasing)

现在轮到链表了。还记得第一部分讲的吗？链表的节点散落在内存的各个角落。

场景： 你遍历一个链表 Node A -> Node B -> Node C。
过程：
1. 访问 Node A： CPU 去内存读 A。内存把 A 以及 A 旁边的一堆数据（可能是其他不相关的变量）打包发给 CPU。
2. 寻找 Node B： CPU 读完 A，拿到了 next 指针，指向十万八千里外的地址 0x9999。
3. 悲剧发生： CPU 查了一下缓存，发现只有 A 周围的数据，根本没有 0x9999 的影子。
4. Cache Miss（缓存未命中）： CPU 被迫停下来，再次向慢速的内存发出请求："给我 0x9999 的数据。"
5. 等待： CPU 发呆几百个时钟周期。
6. 访问 Node C： 拿到 B 后，发现 C 在另一个遥远的地址。再次 Cache Miss，再次等待。

这种现象在计算机领域有个专门的术语，叫 Pointer Chasing（指针追逐） 。不管你的 CPU 频率有多高（3GHz, 5GHz），由于必须等上一个节点的数据到了才能知道下一个节点的地址，CPU 的流水线被彻底打断了。

5. 硬件预取器（Hardware Prefetcher）的困惑

现代 CPU 还有一个非常智能的功能，叫"预取器"。它会盯着你的内存访问模式。

对数组： 预取器看到你依次访问 100, 104, 108，它会立刻猜到："哈！这小子肯定还要访问 112。" 于是它趁你在计算的时候，提前把 112 从内存拉到了缓存里。等你真要用的时候，数据已经在手边了。
对链表： 访问地址是 0x100 -> 0x888 -> 0x205 -> 0xF0A... 毫无规律可言（随机访问）。预取器直接一脸懵逼："我不造你下一步要去哪啊！" 于是预取功能完全失效。

第三部分总结

从系统架构的角度看：

数组是对 CPU 极其友好的结构（空间连续 = 缓存命中 + 硬件预取）。
链表是对 CPU 极其恶劣的结构（空间离散 = 缓存未命中 + 流水线停顿）。

这就是为什么在高性能游戏开发（如《使命召唤》引擎）、高频交易系统或 AI 核心算子中，程序员会尽量避免使用链表。如果你必须存一堆对象，他们甚至会预先分配一个巨大的数组（Object Pool），强行把对象挨个放进去，用数组下标代替指针，就是为了骗过 CPU，让它以为这是个数组。

下一步 尽管链表有这么多性能缺陷，但它依然是操作系统内核（Kernel）和文件系统的基石。因为还有一种特殊的链表，它不仅解决了单向奔跑的痛苦，还能构建出复杂的数据结构。

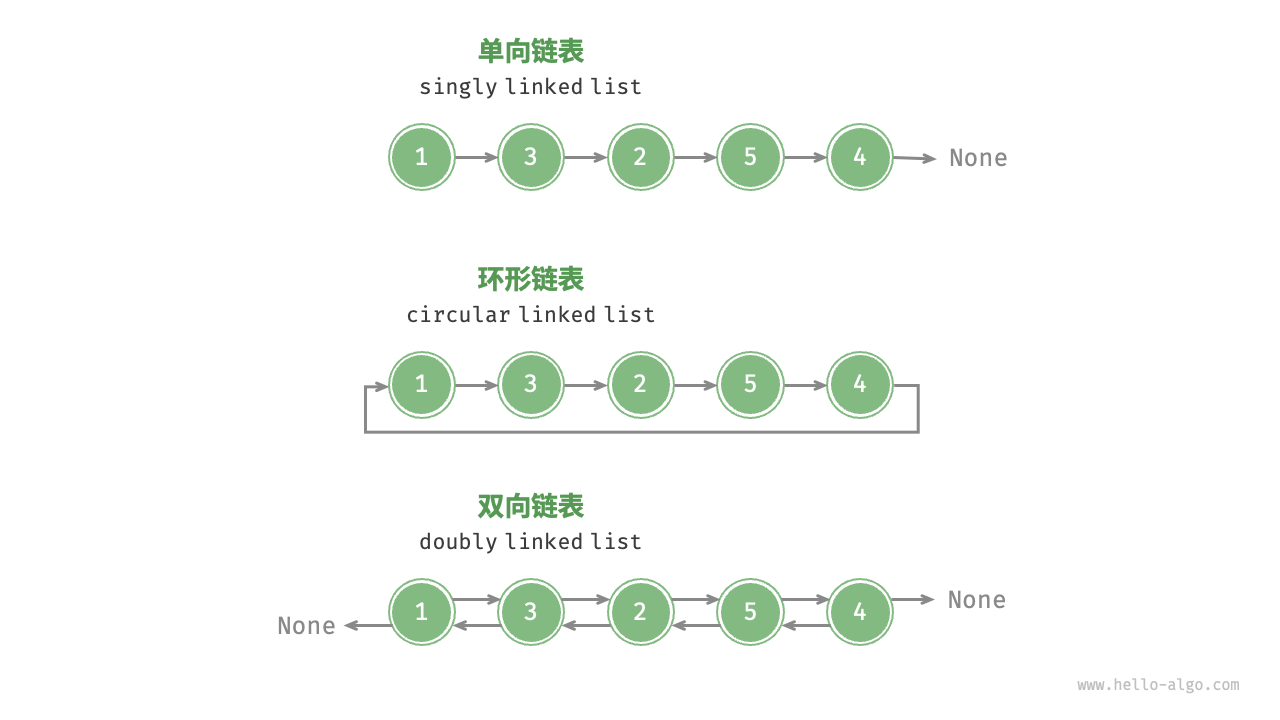
第四部分：双向链表与环形链表------操作系统的核心齿轮

1. 双向链表：给自己留条后路

单向链表最大的痛苦是什么？是删除节点。

如果你想删除节点 B (A -> B -> C)，你手里光攥着 B 的地址是没用的。
为什么？因为你不知道 谁指向了 B（也就是找不到 A）。
你必须从头（Head）开始遍历，直到发现有一个人的 next 是 B，你才能把那个人的手从 B 身上松开，改牵 C。

双向链表完美解决了这个问题。它在内存里是这样存的：

cs 复制代码

struct Node {
    Node* prev;  // 新增：指向"前一个节点"的地址
    int data;    // 数据
    Node* next;  // 指向"后一个节点"的地址
};

它的超能力：原地"自杀"

现在，如果你手里拿着节点 B 的地址，想把它从链表中删掉：

回头看： 通过 B->prev 找到 A。
往前看： 通过 B->next 找到 C。
手术：
- 告诉 A："你的下一个不再是我了，是 C。" (A->next = C)
- 告诉 C："你的前一个不再是我了，是 A。" (C->prev = A)
结果： B 成功脱身，A 和 C 连在了一起。

代价： 内存开销更大了。现在存一个整数，不仅要送一个 next 指针，还要送一个 prev 指针。在 64 位系统上，光是指针就占了 16 字节，而数据可能才 4 字节。有效载荷极低。

2. 循环链表：衔尾蛇（Ouroboros）

循环链表既可以是单向的，也可以是双向的。它的唯一特点是： 没有尽头（NULL）。 最后一个节点的 next 指针，指向了第一个节点。

这看起来像个死循环 BUG，但在计算机底层，这是处理周期性任务的神器。

3. 真实世界的底层应用：操作系统怎么用它们？

你现在的电脑虽然只有一个鼠标，但同时跑着浏览器、音乐播放器、微信。CPU 是怎么做到"同时"处理它们的？其实是轮流宠幸。

场景一：CPU 进程调度（Round Robin 调度）

操作系统底层维护了一个循环链表，里面挂着所有正在运行的程序：

CPU 执行"浏览器" 10 毫秒。
时间到！CPU 顺着链表找到下一个节点"微信"。
CPU 执行"微信" 10 毫秒。
时间到！找下一个"音乐"。
... 转了一圈又回到"浏览器"。

因为是环形的，调度器永远不需要担心"走到头了怎么办"，它可以无限循环下去，保证每个程序都能分到时间片。

场景二：LRU 缓存淘汰算法（双向链表的高光时刻）

这是大厂面试最爱考的题：设计一个缓存，满了之后，把最近最少使用（Least Recently Used）的数据踢掉。

这里的核心数据结构，就是哈希表 + 双向链表。

链表的作用： 维护顺序。
- 链表头放最新访问过的数据。
- 链表尾放很久没碰过的旧数据。

为什么一定要双向链表？
- 当你再次访问了一个旧数据（在链表中间），你需要把它揪出来，移动到链表头。
- 这个"揪出来"的动作，本质就是删除节点 + 头部插入。
- 正如前面所说，只有双向链表才能在 O(1) 时间内完成"原地删除"（不需要从头遍历找前驱）。

如果用数组做 LRU，每次移动数据都要把其他数据往后挪，性能直接爆炸。在这里，双向链表是无可替代的。

第四部分总结

双向链表： 用更多的空间（两个指针），换取了反向遍历 和O(1) 原地删除的能力。
循环链表： 专门用于处理轮询、缓冲区等没有终点的任务。
地位： 虽然在高性能数值计算中不如数组，但在系统设计（调度、缓存、内存管理）中，复杂的链表结构是绝对的统治者。

下一步 讲到底层，链表其实还有一个最最基础、但99%的人都不知道的用途。当你写 C 语言的 malloc 或者 C++ 的 new 申请内存时，操作系统怎么知道哪块内存是空的，哪块是满的？

答案是：空闲内存本身就是一张巨大的链表。这是计算机内存管理的终极奥义。

第五部分：内存分配器（Malloc）的秘密------空闲链表（Free List）与内存碎片

你可能会好奇：当我们创建一个链表时，我们需要用 malloc 去申请内存。但是，malloc 自己又是怎么管理内存的呢？

答案是：它用链表来管理链表。

这是一个"我知道你没衣服穿，所以我把我的皮扒下来给你穿"的故事。

1. 堆内存（Heap）的混沌状态

当你启动一个程序时，操作系统会划给你一大块空白的内存区域，叫做堆（Heap）。这块地一开始是纯白茫茫一片，没有任何结构。

随着程序运行，你一会儿 malloc(10)，一会儿 malloc(1000)，一会儿又 free 掉中间的一块。这时候，内存就变成了奶酪------这里有个洞，那里有块肉，中间又有个洞。

核心难题： 当下次你喊 malloc(50) 的时候，分配器（Allocator）怎么知道哪里的"洞"刚好能塞下这 50 个字节？

它需要一张地图。这张地图，就是空闲链表（Free List）。

2. 极致的节省：把数据存进"垃圾"里

通常我们做链表，需要额外申请内存来存节点（Node）。但在内存管理器里，我们不能再申请内存了（因为我就是管内存的，我再去申请，那是套娃）。

既然这块内存是"空闲"的（也就是里面的数据是垃圾，没人用），那为什么不把链表的指针 直接写在这个空闲内存块的肚子里呢？

在底层的空闲内存块中，结构是这样的：

头部 (Hidden)	空闲区域 (User Data Area)
记录大小	[Prev 指针] [Next 指针] ... (剩余的垃圾空间) ...

Header: 记录这块空闲地有多大（比如 100 字节）。
Body: 因为现在没人用，malloc 偷偷在里面写了两个地址：
- Prev: 上一块空闲地在哪？
- Next: 下一块空闲地在哪？

结论： 操作系统不需要花费哪怕 1 个字节的额外空间来维护这张表。它利用"废弃之物"连接成了管理的纽带。

3. Malloc 的过程：链表遍历

当你调用 p = malloc(64) 时：

遍历： 分配器从 Free List 的头开始，顺着 Next 指针遍历每一个空闲块。
寻找（First Fit 算法）：
- 空闲块 A：只有 32 字节。不够，跳过。
- 空闲块 B：有 1000 字节。太棒了，够用了！
切割（Splitting）：
- 它不会把 1000 字节全给你。它会像切蛋糕一样，切下 64 字节给你。
- 剩下的 1000 - 64 = 936字节，依然留在链表里，只是 Header 里的"大小"改了一下，位置稍微往后挪了一点。
返回： 把那 64 字节的地址返回给你。

4. Free 的过程：链表合并（Coalescing）

当你调用 free(p) 时：

回收： 你的这 64 字节内存被收回了。
插入链表： 分配器把这块地重新挂回到 Free List 链表上，并在里面写上 Prev / Next 指针。

关键步骤：合并（Merge） 如果仅仅是挂回去，内存会变得越来越碎（全是小渣渣）。分配器会非常聪明地检查：

左顾： "我的左边邻居是空闲的吗？" 如果是，咱们合体，变成一个大块。
右盼： "我的右边邻居是空闲的吗？" 如果是，咱们也合体。

通过链表，分配器把无数个小碎片重新粘合成了一大块完整的空闲地，以此抵抗内存碎片化。

5. 内存碎片（Fragmentation）------链表的宿敌

虽然有"合并"机制，但链表管理的内存依然会面临外部碎片（External Fragmentation） 的诅咒。

场景： 内存里有 100MB 空间，但是被切得稀碎： [10MB空] [1MB用] [10MB空] [1MB用] ...

现状： 总空闲内存 = 50MB。
请求： malloc(20MB)。
结果： 失败！（Out of Memory）。

为什么？因为虽然总数够，但链表里没有单独的一个节点 能一次性拿出 20MB 的连续空间。

这就是为什么像 Java、Go、Python 这种带有垃圾回收（GC） 的语言，通常不只是简单的链表管理，它们还会做 Compaction（压缩/整理）：把所有正在用的内存强行推到一边，把所有空闲的内存挤到另一边，强行把链表"拍扁"成一大块数组。

第五部分总结

从最底层的视角来看：

本质： 你的内存条，本质上就是一个巨型、动态变化的链表。
技巧： 它是"隐形链表"，指针直接存储在未使用的内存空间里。
代价： 这种基于链表的管理方式，会导致内存碎片，最终可能导致系统有内存却无法分配。

链表常用操作

初始化链表：

python 复制代码

# 初始化链表 1 -> 3 -> 2 -> 5 -> 4
# 初始化各个节点
n0 = ListNode(1)
n1 = ListNode(3)
n2 = ListNode(2)
n3 = ListNode(5)
n4 = ListNode(4)
# 构建节点之间的引用
n0.next = n1
n1.next = n2
n2.next = n3
n3.next = n4

插入节点：

python 复制代码

def insert(n0: ListNode, P: ListNode):
    """在链表的节点 n0 之后插入节点 P"""
    n1 = n0.next
    P.next = n1
    n0.next = P

删除节点

python 复制代码

def remove(n0: ListNode):
    """删除链表的节点 n0 之后的首个节点"""
    if not n0.next:
        return
    # n0 -> P -> n1
    P = n0.next
    n1 = P.next
    n0.next = n1

访问节点

python 复制代码

def access(head: ListNode, index: int) -> ListNode | None:
    """访问链表中索引为 index 的节点"""
    for _ in range(index):
        if not head:
            return None
        head = head.next
    return head

查找结点：

python 复制代码

def find(head: ListNode, target: int) -> int:
    """在链表中查找值为 target 的首个节点"""
    index = 0
    while head:
        if head.val == target:
            return index
        head = head.next
        index += 1
    return -1