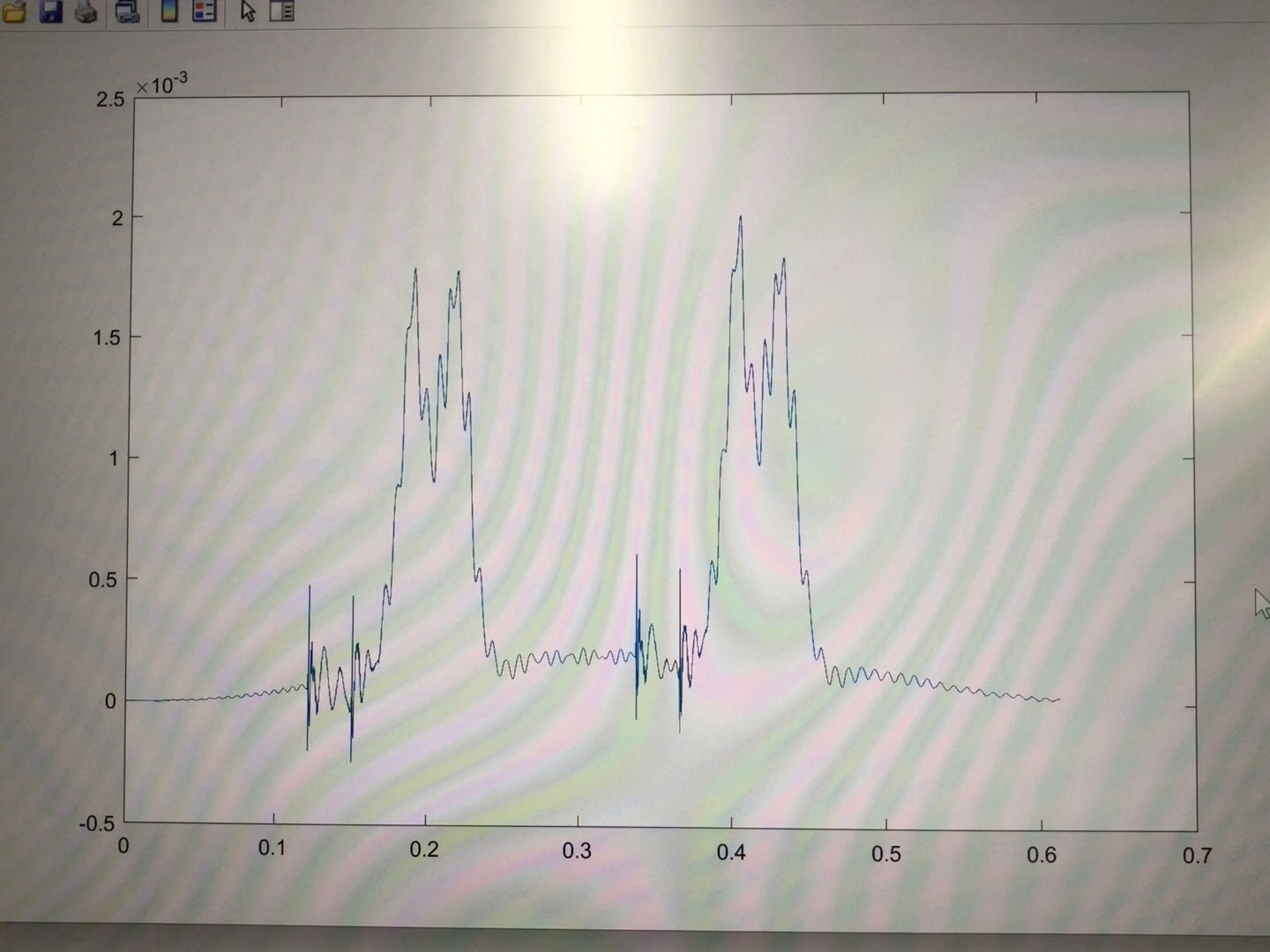
车桥耦合matlab程序。 使用newmark法进行数值积分，考虑不平顺车辆-无砟轨道-桥梁耦...

车桥耦合matlab程序。 使用newmark法进行数值积分，考虑不平顺车辆-无砟轨道-桥梁耦合的动力学求解全套

直接上干货！最近在搞车桥耦合动力学分析，发现用Matlab实现Newmark-β法解这种多体耦合系统特别带劲。今天就带大家手撕代码，顺便聊聊怎么处理不平顺激励下的振动传递问题。

先说核心架构，咱们的模型包含三个模块：二自由度车辆模型、无砟轨道梁单元模型、桥梁实体单元。耦合的关键在于轮轨接触力的迭代计算，这里用Hertz非线性接触理论实现：

function F = Hertz_contact(z1, z2)
    G = 8.43e10; % 轮轨接触常数
    delta = max(z1 - z2, 0); % 轮轨压缩量
    F = G * delta^(3/2); % 非线性赫兹力
end

这个函数会在每个时间步被反复调用，注意max函数处理轮轨分离的情况，避免出现虚接触。

时间积分部分采用改进的Newmark-β法，比常规版本更适应强非线性问题：

beta = 0.25; gamma = 0.5; % 经典参数配置
dt = 0.001; % 时间步长要小于最小振动周期1/10
for k = 1:nt-1
    % 预测步
    v_pred = v(:,k) + (1-gamma)*dt*a(:,k);
    d_pred = d(:,k) + dt*v(:,k) + (0.5-beta)*dt^2*a(:,k);
    
    % 残差计算
    [Fc, Jc] = Contact_Jacobian(d_pred); % 接触力及其雅可比
    R = M*a(:,k) + C*v_pred + K*d_pred - Fc - F_ext;
    
    % 修正步
    a(:,k+1) = (M + gamma*dt*C + beta*dt^2*K - Jc) \ R;
    v(:,k+1) = v_pred + gamma*dt*a(:,k+1);
    d(:,k+1) = d_pred + beta*dt^2*a(:,k+1);
end

这里把接触力的雅可比矩阵Jc显式加入系数矩阵，显著提升收敛速度。注意雅可比矩阵要包含轮轨、轨桥多个接触对的导数。

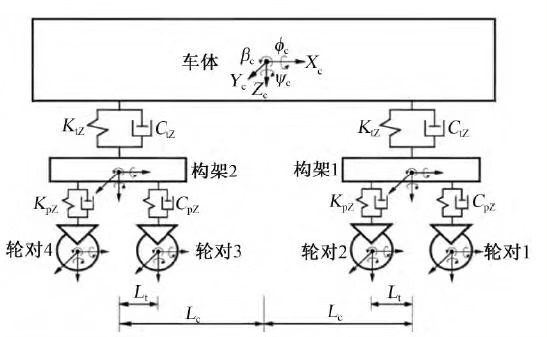
处理轨道不平顺时，采用德国低干扰谱生成随机激励：

function rough = track_roughness(L, dx)
    n = round(L/dx);
    phi = (0:n-1)'*2*pi/n;
    S = 0.00012./((0.1:0.1:10).^2 + 0.25); % 频谱密度
    rough = real(ifft(sqrt(S).*exp(1i*phi))); 
end

生成的不平顺信号记得要做零均值处理，否则会导致系统漂移。

计算结果后处理时，重点关注车体加速度和桥梁跨中位移：

figure('Position',[200,200,800,300])
subplot(121)
plot(t, acc_vehicle*9.8)
title('车体垂向加速度(g)')
xlabel('时间/s'), grid on

subplot(122)
plot(t, disp_bridge(round(nb/2),:)*1000)
title('桥梁跨中位移(mm)')
xlabel('时间/s'), grid tight

这种对比图能直观看出振动传递规律。注意桥梁位移要取跨中节点，那是响应最大的位置。

几个踩坑经验：

1. 质量矩阵千万别用集中质量矩阵，用一致质量矩阵更稳定
2. 时间步长超过1e-3秒容易发散，特别是存在钢轨扣件非线性时
3. 桥梁阻尼比建议取2%-5%，实测数据校准很重要
4. 并行计算加速技巧：把接触力计算改成Mex函数

完整跑完一个30秒的工况大概需要15分钟（i7-12700H），建议先调试5秒内的短工况。收敛性检查看能量误差是否小于1e-4，残差范数是否持续下降。

最后说个骚操作：把实时位移导出成AVI动画，用getframe捕捉模型振动形态，汇报时效果直接拉满。不过注意别让老板发现你在用游戏显卡跑有限元------虽然真的快很多。