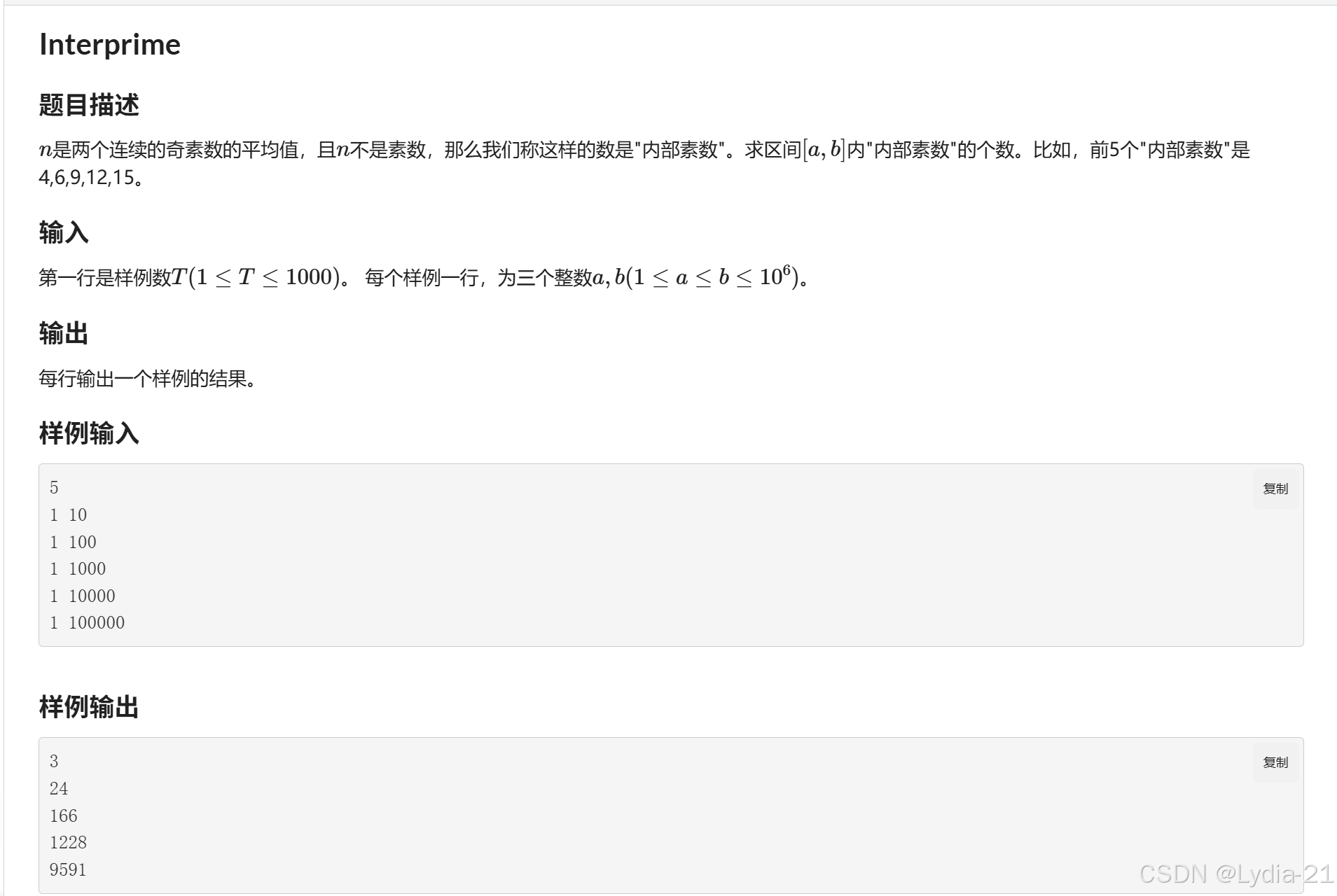
题目
思路
奇素数的核心数学特性
- 所有素数中,只有 2 是偶数,其余素数都是奇数(奇素数)。
- 两个奇数相加的结果是偶数,因此 "连续奇素数对(prev, i)" 的和
prev + i一定是偶数,它们的平均值avg = (prev + i) / 2必然是整数(比如 3 和 5 的平均值是 4,5 和 7 的平均值是 6)。 - 连续的奇素数之间没有其他素数(否则就不是 "连续" 的),因此它们的平均值
avg一定不是素数(比如 3 和 5 之间的数是 4,不是素数;5 和 7 之间的数是 6,不是素数)
接下来就是利用这个特性编写代码了。
首先用欧拉筛先计算1e6+100以内的素数,多算一点避免漏掉一些情况,比如说两个相邻的素数刚好有个在1e6左边,还有一个在右边一点,然后平均值还是在1e6内,那这样你在右边一点的那个素数也能考虑到。
接着就是定义一个prev 存左边的奇质数,初始化为primes[1],然后遍历N以内所有的质数 ,每次取出一个素数,然后取平均值,判断其如果不是素数而且在范围内,那个这个平均值就是满足要求的内部素数,然后再把prev设置为当前的primes[i],相当于向右移动了一个单位。这里注意一点我们的循环条件应该设置为i<cnt,而不是primes[i]<=N,因为我们欧拉筛的范围保证了这个条件恒真,所以会越界从而出错,而i<cnt,i++,总是能在正确的时候结束。
计算[a,b]内满足要求的所有内部素数的个数问题,看到区间和,就想到前缀和 ,所以我设置一个f数组,初始化为0,如果avg是满足要求的内部素数,那么f[avg]=1,这是为了方便统计个数,再计算前缀和数组,f[i]+=f[i-1],这里相当于把 f 计算完前缀和以后又赋值给 f,因为这里我们并不需要知道具体那个数是不是内部素数,而是关注的是个数。
[a,b]之间的个数,用f[b]-f[a-1]即可,f[i]表示的是从1到 i 之间,所有内部素数的个数。
代码
cpp
#include<stdio.h>
#define N 2000000
typedef enum{false,true} bool;
int T,a,b;
int cnt=0,primes[N+1];
bool st[N+1]={false};
int f[N+1]={0};
void generate_primes(){
for(int i=2;i<=N;i++){
if(!st[i]) primes[cnt++]=i;
for(int j=0;j<cnt&&primes[j]<=N/i;j++){
st[primes[j]*i]=true;
if(i%primes[j]==0) break;
}
}
}
void Interprime(){
int prev=primes[1];
for(int i=2;primes[i]<=N;i++){
int avg=(prev+primes[i])/2;
if(st[avg]) f[avg]=1;
prev=primes[i];
}
for(int i=1;i<=N;i++)
f[i]+=f[i-1];
}
int main(){
generate_primes();
Interprime();
scanf("%d",&T);
while(T--){
scanf("%d%d",&a,&b);
int ans=f[b]-f[a-1];
printf("%d\n",ans);
}
return 0;
}