84. 柱状图中最大的矩形【困难】

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

复制代码

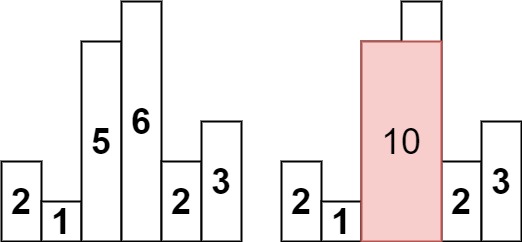
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

复制代码

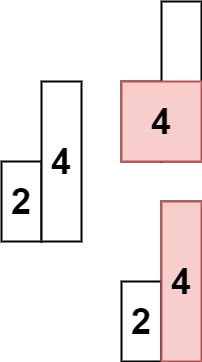
输入： heights = [2,4]
输出： 4

一、单调栈

思路：

这题考的基础模型其实就是：在一维数组中对每一个数找到第一个比自己小的元素。这类"在一维数组中找第一个满足某种条件的数"的场景就是典型的单调栈应用场景。

这一题需要找到是每一个柱子左边和右边第一个比它矮的柱子，我们取它俩的下标，然后用

right - left - 1来计算矩形的宽，这样我们就可以计算出以这个柱子为高度的最大矩形的面积。

我们定义一个单调递增的栈来存数组元素的下标，也就是在遍历数组时，每次只压入更大的元素的下标，并且在遍历时判断该元素 x 是否大于栈顶元素，若大于则入栈，若小于则 x 元素的下标就是右边界，而左边界就是栈中的第二个元素，找到了左右两边小于栈顶元素的下标，就能计算宽，再乘以栈顶元素的值，就得到以栈顶元素的值为高的矩形的面积。

注意我们找到的是以栈顶元素的值为高的矩形的面积，不是元素 x。要做弹出栈顶元素的操作。

如果左边界也就是栈中第二个元素没有了，栈为空了，那就记左边界为 -1，这样计算是对的，已经经过数学验证。如果遍历完数组，栈中还有元素，那么这些元素的右边界都是数组末尾，左边界还是栈中第二个元素，我们分别计算完这些剩余元素对应的矩形面积。

有一个小技巧，在数组最后加一个元素 0 ，用来处理遍历完后栈中剩余的元素，加上末尾 0 后，当遍历到最后，这样在比较栈顶元素和当前元素时，当前元素为0，那一定小于栈顶元素，都能找到右边界 0 的下标，都能按照非剩余元素那样计算面试，就可以和非剩余元素用一样的代码计算。不用再写新代码处理栈中剩余元素。

时间复杂度O(n)

代码：

java 复制代码

class Solution {
    public int largestRectangleArea(int[] heights) {
        int maxArea = 0;
        int n = heights.length;
        Stack<Integer> stack = new Stack<>();

        for(int i = 0; i <= n; i++){
            // 末尾加一个0，让处理栈中剩余元素和处理非剩余元素用一样的代码
            int curHeight = (i == n) ? 0 : heights[i];

            // 栈不为空且该元素小于栈顶元素
            while(!stack.isEmpty() && curHeight < heights[stack.peek()]){
                // 计算高
                int height = heights[stack.pop()];

                // 计算宽,这里很巧妙，因为上面已经pop出栈了栈顶元素，所以这里的peek是栈中第二个元素，也就左边界
                int width = stack.isEmpty() ? i : i - stack.peek() - 1;

                maxArea = Math.max(maxArea, height * width);
            }

            stack.push(i);
        }

        return maxArea;
    }
}