车辆七自由度动力学模型
本文介绍了车辆七自由度动力学模型,该模型能更准确描述打滑和侧滑等复杂工况下的车辆行为。文章首先对比了二/三自由度模型的局限性,然后详细推导了七自由度模型的核心方程,包括纵向、横向和横摆三个整车运动方程,以及四个车轮的转动方程。模型考虑了轮胎垂向载荷的动态分配、侧偏角计算、滑移率计算等关键因素,并采用魔术公式描述轮胎力特性。文章还给出了转弯制动联合工况下轮胎力的修正方法,以及相关参数的参考值,为车辆动力学仿真和分析提供了理论基础。
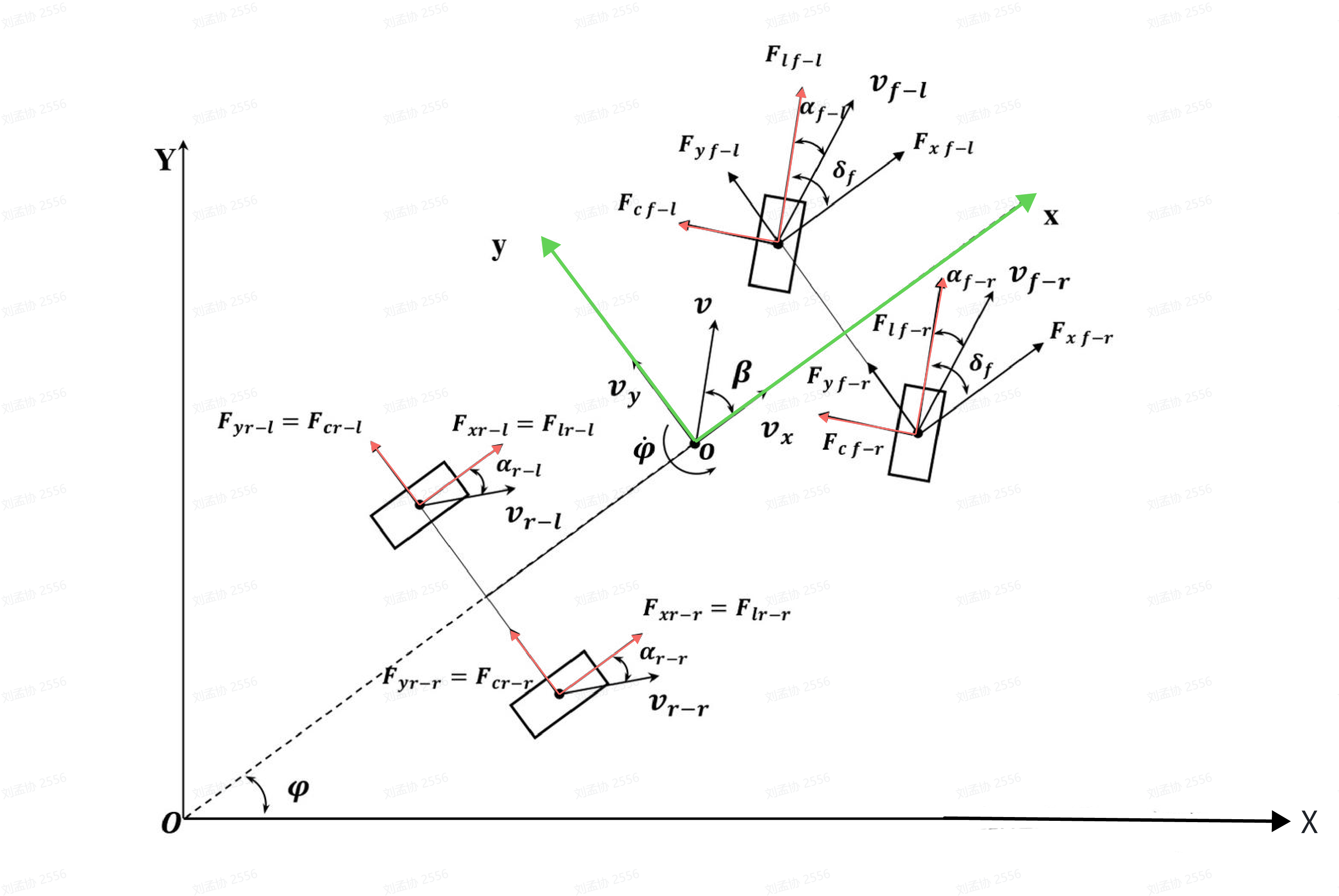
三自由度整车模型
纵向力平衡方程:
m(vx˙−ωvy)=(Fxfl+Fxfr)cosδ−(Fyfl+Fyfr)sinδ+Fxrl+Fxrr m (\dot{v_x}-\omega v_y)=(F_{xfl} + F_{xfr})cos{\delta} - (F_{yfl}+ F_{yfr})sin{\delta} + F_{xrl}+F_{xrr} m(vx˙−ωvy)=(Fxfl+Fxfr)cosδ−(Fyfl+Fyfr)sinδ+Fxrl+Fxrr
横向力平衡方程:
m(vy˙+ωvx)=(Fxfl+Fxfr)sinδ+(Fyfl+Fyfr)cosδ+Fyrl+Fyrr m (\dot{v_y}+\omega v_x)=(F_{xfl} + F_{xfr})sin{\delta} + (F_{yfl}+ F_{yfr})cos{\delta} + F_{yrl}+F_{yrr} m(vy˙+ωvx)=(Fxfl+Fxfr)sinδ+(Fyfl+Fyfr)cosδ+Fyrl+Fyrr
绕Z轴的力矩平衡方程
Izω˙=[(Fxfl+Fxfr)sinδ+(Fyfl+Fyfr)cosδ]a+[(Fxfr−Fxfl)cosδ+(Fyfl+Fyfr)sinδ]tw12+(Fxrr−Fxrl)tw22−(Fyrl+Fyrr)b \begin{align*} I_z \dot{\omega} &=[(F_{xfl} + F_{xfr})sin{\delta} + (F_{yfl}+ F_{yfr})cos{\delta}] a \\ &+[(F_{xfr} - F_{xfl})cos{\delta}+ (F_{yfl}+ F_{yfr})sin{\delta}] \frac{t_{w1}}{2} \\ &+(F_{xrr}-F_{xrl}) \frac{t_{w2}}{2} \\ &- (F_{yrl}+F_{yrr})b \end{align*} Izω˙=[(Fxfl+Fxfr)sinδ+(Fyfl+Fyfr)cosδ]a+[(Fxfr−Fxfl)cosδ+(Fyfl+Fyfr)sinδ]2tw1+(Fxrr−Fxrl)2tw2−(Fyrl+Fyrr)b
上述方程中:
- δδδ为前轮转角;
- vx,vyv_x,v_yvx,vy分别为纵向、横向车速;
- βββ为质心侧偏角;ω\omegaω为横摆角速度;
- Fxi、Fyi、FziFxi、Fyi、FziFxi、Fyi、Fzi分别为轮胎纵向力、侧向力、垂向力;
- mmm为整车质量;
- a、ba、ba、b为前后轴到质心的距离;
- tw1t_{w1}tw1为前轴轮距;tw2t_{w2}tw2为后轴轮距;IzI_zIz为整车绕Z轴的转动惯量;hgh_ghg为质心到地面的距离.
计算各轮胎的垂向载荷
左前轮静态载荷与动态载荷:Fzfl=mgb2L−mvx˙hg2L−mvy˙hgbtw1L左前轮静态载荷与动态载荷: F_{zfl}=mg\frac{b}{2L}-m\dot{v_x}\frac{h_g}{2L}-m\dot{v_y}\frac{h_g b}{t_{w1} L} 左前轮静态载荷与动态载荷:Fzfl=mg2Lb−mvx˙2Lhg−mvy˙tw1Lhgb
右前轮静态载荷与动态载荷:Fzfl=mgb2L−mvx˙hg2L+mvy˙hgbtw1L右前轮静态载荷与动态载荷: F_{zfl}=mg\frac{b}{2L}-m\dot{v_x}\frac{h_g}{2L}+m\dot{v_y}\frac{h_g b}{t_{w1} L} 右前轮静态载荷与动态载荷:Fzfl=mg2Lb−mvx˙2Lhg+mvy˙tw1Lhgb
左后轮静态载荷与动态载荷:Fzfl=mgb2L−mvx˙hg2L−mvy˙hgatw1L左后轮静态载荷与动态载荷: F_{zfl}=mg\frac{b}{2L}-m\dot{v_x}\frac{h_g}{2L}-m\dot{v_y}\frac{h_g a}{t_{w1} L} 左后轮静态载荷与动态载荷:Fzfl=mg2Lb−mvx˙2Lhg−mvy˙tw1Lhga
右后轮静态载荷与动态载荷:Fzfl=mgb2L−mvx˙hg2L+mvy˙hgatw1L右后轮静态载荷与动态载荷: F_{zfl}=mg\frac{b}{2L}-m\dot{v_x}\frac{h_g}{2L}+m\dot{v_y}\frac{h_g a}{t_{w1} L} 右后轮静态载荷与动态载荷:Fzfl=mg2Lb−mvx˙2Lhg+mvy˙tw1Lhga
计算各轮胎的侧偏角
左前轮侧偏角:αfl=δ−arctan(vy+ωavx−tw12ω)左前轮侧偏角: \alpha_{fl}=\delta - arctan(\frac{v_y+\omega a}{v_x-\frac{t_{w1}}{2}\omega} ) 左前轮侧偏角:αfl=δ−arctan(vx−2tw1ωvy+ωa)
右前轮侧偏角:αfr=δ−arctan(vy+ωavx+tw12ω)右前轮侧偏角: \alpha_{fr}=\delta - arctan(\frac{v_y+\omega a}{v_x+\frac{t_{w1}}{2}\omega} ) 右前轮侧偏角:αfr=δ−arctan(vx+2tw1ωvy+ωa)
左后轮侧偏角荷:αrl=−arctan(vy−ωbvx−tw22ω)左后轮侧偏角荷: \alpha_{rl}=- arctan(\frac{v_y-\omega b}{v_x-\frac{t_{w2}}{2}\omega} ) 左后轮侧偏角荷:αrl=−arctan(vx−2tw2ωvy−ωb)
右后轮侧偏角:αrr=−arctan(vy−ωbvx+tw22ω)右后轮侧偏角: \alpha_{rr}=- arctan(\frac{v_y-\omega b}{v_x+\frac{t_{w2}}{2}\omega} ) 右后轮侧偏角:αrr=−arctan(vx+2tw2ωvy−ωb)
计算各轮胎的滑移率
轮胎坐标系中的各轮胎的纵向速度
Vtfl=(vx−tw12ω)cosδ+(vy+ωa)sinδ V_{tfl}=(v_x-\frac{t_{w1}}{2}\omega)cos\delta+(v_y+\omega a)sin\delta Vtfl=(vx−2tw1ω)cosδ+(vy+ωa)sinδ
Vtfr=(vx+tw12ω)cosδ+(vy+ωa)sinδ V_{tfr}=(v_x+\frac{t_{w1}}{2}\omega)cos\delta+(v_y+\omega a)sin\delta Vtfr=(vx+2tw1ω)cosδ+(vy+ωa)sinδ
Vtrl=vx−tw22ω V_{trl}=v_x-\frac{t_{w2}}{2} \omega Vtrl=vx−2tw2ω
Vtrr=vx+tw22ω V_{trr}=v_x+\frac{t_{w2}}{2} \omega Vtrr=vx+2tw2ω
计算各轮胎的滑移率
λfl=Vtfl−ωRVtfl \lambda_{fl}=\frac{V_{tfl} - \omega R}{V_{tfl}} λfl=VtflVtfl−ωR
λfl=Vtfr−ωRVtfr \lambda_{fl}=\frac{V_{tfr} - \omega R}{V_{tfr}} λfl=VtfrVtfr−ωR
λfl=Vtrl−ωRVtrl \lambda_{fl}=\frac{V_{trl} - \omega R}{V_{trl}} λfl=VtrlVtrl−ωR
λfl=Vtrr−ωRVtrr \lambda_{fl}=\frac{V_{trr} - \omega R}{V_{trr}} λfl=VtrrVtrr−ωR
轮胎魔术公式
魔术公式的统一形式为:
{Y(x)=y(x)+Svy(x)=D∗sin(Carctan[Bx−E(Bx−arctanBx)])x=X+Sh \begin{cases} Y(x)&=y(x)+S_v \\ y(x)&=D*sin(C arctan[Bx-E(Bx-arctanBx)]) \\ x&=X+S_h \end{cases} ⎩ ⎨ ⎧Y(x)y(x)x=y(x)+Sv=D∗sin(Carctan[Bx−E(Bx−arctanBx)])=X+Sh
其中,YYY为侧向力、纵向力或回正力矩;XXX为侧偏角或纵向滑移率;DDD为峰值因子;BBB为刚度因子;CCC为曲线形状因子;EEE为曲线曲率因子;ShS_hSh为曲线水平方向漂移;SvS_vSv为曲线垂直方向漂移。
根据魔术公式的一般形式,可以得到轮胎的侧向力与侧偏角、轮胎垂直载荷之间的关系:
{Fy=D∗sin(Carctan[Bx−E(Bx−arctanBx)])+Svx=α+Sh \begin{cases} F_y & = D*sin(C arctan[Bx-E(Bx-arctanBx)])+S_v \\ x &=\alpha+S_h \end{cases} {Fyx=D∗sin(Carctan[Bx−E(Bx−arctanBx)])+Sv=α+Sh
其中:
C=1.3C=1.3C=1.3
D=a1Fz2+a2FzD=a_1 F^2_z + a_2 F_zD=a1Fz2+a2Fz
B∗C∗D=a3sin[a4arctan(a5Fz)](1−a12∣γ∣)B*C*D=a_3 sin[a_4 arctan(a_5 F_z)] (1-a_{12} \vert \gamma \vert)B∗C∗D=a3sin[a4arctan(a5Fz)](1−a12∣γ∣)
B=B∗C∗D/C/DB=B*C*D/C/DB=B∗C∗D/C/D
Ey=a6Fz2+a7Fz+a8E_y=a_6 F^2_z + a_7F_z +a_8Ey=a6Fz2+a7Fz+a8
Sh=a9γS_h=a_9 \gammaSh=a9γ
Sv=(a10Fz2+a11Fz)γS_v=(a_{10}F^2_z+a_{11}F_z) \gammaSv=(a10Fz2+a11Fz)γ
γ\gammaγ为车轮外倾角,a1,...a12为拟合参数a_1,...a_{12}为拟合参数a1,...a12为拟合参数.
车轮外倾角是车轮平面与车辆坐标轴的垂直轴的交角,在设为理想情况下,不考虑车轮外倾角和漂移的影响,即轮胎侧倾角y为0,Sh,SvS_h,S_vSh,Sv分别为0。各
拟合参数可参考如下:

对于转弯制动联合工况 而言,轮胎的纵向力和侧偏力需要做一些修正,具体如下:
{Fx=ϵxϵFx0Fx=ϵyϵFy0 \begin{cases} F_x=\frac{\epsilon_x}{\epsilon} F_{x0} \\ F_x=\frac{\epsilon_y}{\epsilon} F_{y0} \\ \end{cases} {Fx=ϵϵxFx0Fx=ϵϵyFy0
其中:ϵ=ϵx2+ϵy2,ϵx=λ1+λ,ϵy=tanα1+λ\epsilon=\sqrt{\epsilon_x^2 + \epsilon_y^2},\epsilon_x=\frac{\lambda}{1+\lambda},\epsilon_y=\frac{tan\alpha}{1+\lambda}ϵ=ϵx2+ϵy2 ,ϵx=1+λλ,ϵy=1+λtanα
参考文献
https://blog.csdn.net/qingfengxd1/article/details/109851881?login=from_csdn