通过超宽带信号估计位置------论文精读
S. Gezici and H. V. Poor, "Position Estimation via Ultra-Wide-Band Signals," in Proceedings of the IEEE, vol. 97, no. 2, pp. 386-403, Feb. 2009, doi: 10.1109/JPROC.2008.2008840.
文章的"主线骨架":大带宽 → 高时间分辨率 → TOA 更准 → 定位更准
这篇 invited paper 的叙事相当工整:先解释 UWB 是什么、为什么它在法规限制下仍然适合定位;再给出定位系统的两种体系结构(直接定位 vs 两步定位);随后把"两步法"的第一步(估计 RSS/AOA/TOA/TDOA 等位置相关参数)和第二步(由参数反推坐标)分别讲清;最后把最关键的"时间测距(TOA ranging)"单独拎出来讨论误差来源与算法,并把信号设计与硬件实现作为落地的约束条件。
如果用一句话抓住作者想传达的"根因",就是:UWB 的带宽极大,因而有效带宽 β\betaβ 也大;在 AWGN 单径模型下,TOA 的 CRLB 与 1/(βSNR)1/(\beta\sqrt{\mathrm{SNR}})1/(βSNR ) 成正比,所以 UWB 天生能把时间估计误差压到极小,从而实现厘米级测距/定位的潜力。
1. UWB 的定义与监管约束:从"10 dB 带宽"走到"必须低功率共存"
1.1 10 dB 带宽与分数带宽:式 (1)--(4) 的含义不止是定义
论文采用 FCC 的 UWB 定义:绝对带宽至少 500 MHz 或分数带宽超过 20%。绝对带宽用 10 dB 发射点定义上下截止频率 fL,fHf_L,f_HfL,fH:
B=fH−fL(1) B=f_H-f_L \tag{1} B=fH−fL(1)
中心频率:
fc=fH+fL2(3) f_c=\frac{f_H+f_L}{2} \tag{3} fc=2fH+fL(3)
分数带宽:
Bfrac=Bfc(2) B_{\text{frac}}=\frac{B}{f_c} \tag{2} Bfrac=fcB(2)
代入 (1)(3) 可以得到常见的等价形式:
Bfrac=fH−fL(fH+fL)/2=2(fH−fL)fH+fL(4) B_{\text{frac}} =\frac{f_H-f_L}{(f_H+f_L)/2} =\frac{2(f_H-f_L)}{f_H+f_L} \tag{4} Bfrac=(fH+fL)/2fH−fL=fH+fL2(fH−fL)(4)
这些式子在定位语境下的"更深一层含义"是:带宽越大,时域波形越短,时间分辨率越高 ;而后面 TOA/AOA 的 CRLB 里都会出现有效带宽 β\betaβ,它本质上就是把"频谱能量分布的二阶矩"抽象为一个决定时间分辨率的尺度(附录里会把 β\betaβ 的定义与 Parseval 推导补全)。
1.2 图 1:10 dB 带宽在频域上的几何图像
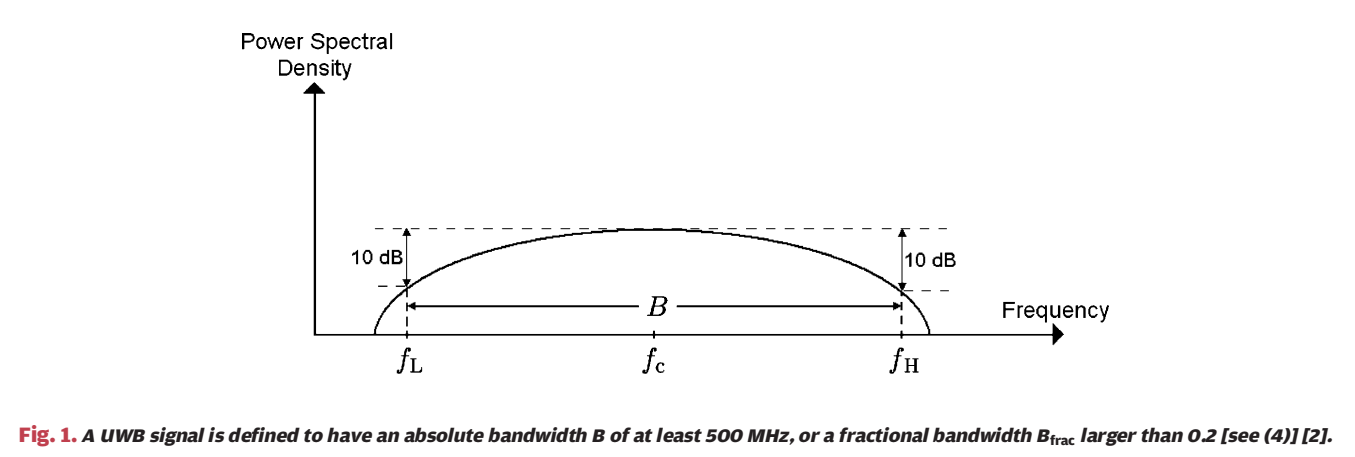
图 1 的纵轴是功率谱密度(Power Spectral Density),横轴是频率。曲线代表某个发射谱形,左右两侧用"相对峰值下降 10 dB 的发射点"定义 fLf_LfL 与 fHf_HfH,两者之间的跨度就是式 (1) 的 BBB,中点则是式 (3) 的 fcf_cfc。图中的虚线标注了 10 dB 的上下界,强调这是一个"工程可测量"的带宽定义,而不是理想数学带宽。
1.3 FCC 发射限值:低功率并不削弱定位,反而改变"提升精度的路径"
为与既有系统共存,FCC 要求 UWB 在 3.1--10.6 GHz 的平均功率谱密度(PSD)不得超过 −41.3 dBm/MHz-41.3\ \mathrm{dBm/MHz}−41.3 dBm/MHz,带外更低,以 Fig.2 举室内通信系统的分段掩膜为例;限值以 EIRP(等效全向辐射功率)表示,测量分辨率带宽是 1 MHz。
1.4 图 2:室内 UWB 的 FCC 掩膜是"分段阶梯",不是一条直线
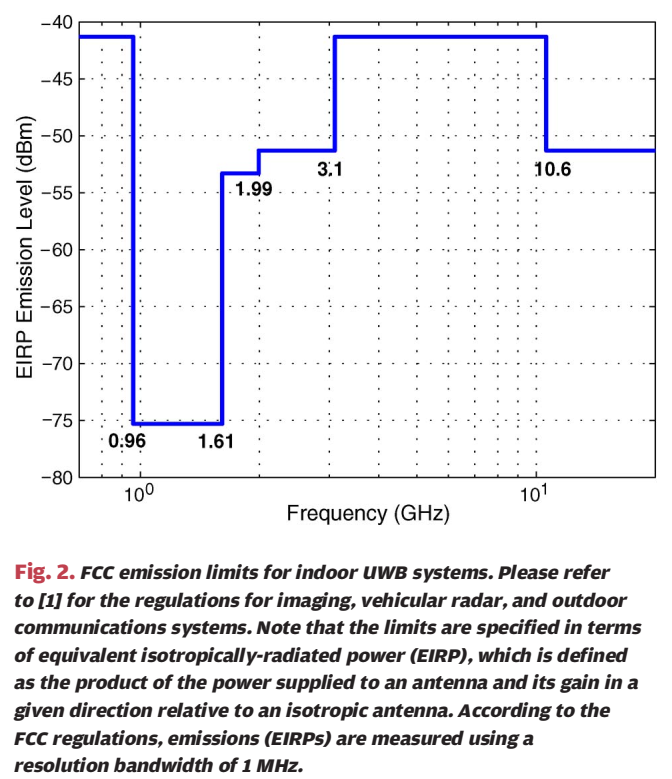
图 2 的横轴是频率(GHz,图上刻度呈对数样式),纵轴是 EIRP emission level(dBm)。蓝色曲线是典型的"阶梯形分段上限":
在 3.1--10.6 GHz 区间,上限约为 −41-41−41 dBm 左右形成平台;在 0.96--1.61 GHz 这一段限值非常低(图上约 −75-75−75 dBm),随后在 1.61--1.99、1.99--3.1 等区间上限逐步抬升,10.6 GHz 之后也会下调。图中标注的 0.96、1.61、1.99、3.1、10.6 等数字是分段边界。
对定位系统而言,这张图隐含一个实用结论:因为平均 PSD 被"压住",定位精度提升不能指望简单增大发射功率,而更依赖 (i) 增大有效带宽 β\betaβ (UWB 先天优势)、(ii) 增加测距前导的时长 TTT 来累积能量、以及 (iii) 更聪明的相关/搜索/首径检测算法与硬件结构 (后文式 (30) 与"SNR∝TPmax\mathrm{SNR}\propto T P_{\max}SNR∝TPmax"就是沿着这条逻辑走的)。
2. IR-UWB 的脉冲结构:低占空比"脉冲列"是定位友好的时间标尺
论文将关注点放在 impulse radio UWB:用极短脉冲、很低的 duty cycle 传输,信息可由脉冲的时序或极性承载;对定位系统而言,核心任务是估计这些脉冲(或其前导结构)的 TOA/TDOA。
图 3:帧间隔 TfT_fTf 与总时长 TTT 是后面"精度--时延--功耗"权衡的坐标轴
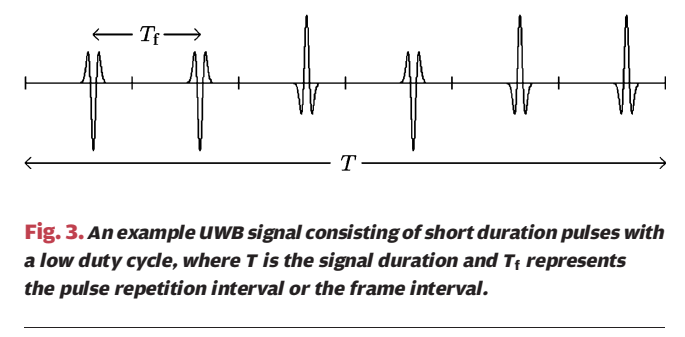
图 3 画的是一串非常窄的双极性脉冲。上方箭头 TfT_fTf 表示相邻脉冲(或帧)之间的间隔(pulse repetition / frame interval),下方箭头 TTT 表示整段信号(常常对应一个用于同步/测距的前导或观测窗口)的总持续时间。直觉上 TTT 越长意味着可累积更多能量,TfT_fTf 越大意味着每帧在平均功率受限时可以"攒"更多能量但峰值功率与多径尾巴问题会变得更敏感;这些都在第四节信号设计里被公式化成"SNR∝TPmax\mathrm{SNR}\propto T P_{\max}SNR∝TPmax"与"TfT_fTf 存在上/下界"。
3. 为什么 UWB 也适合高速通信:式 (5) 的定位含义是"可在低功率下工作"
作者用 Shannon 容量提醒:在 AWGN 信道下
C=Blog2(1+SNR)(bits/s)(5) C=B\log_2(1+\mathrm{SNR})\quad(\mathrm{bits/s}) \tag{5} C=Blog2(1+SNR)(bits/s)(5)
当 BBB 很大时,即便 SNR 不高也能获得可观的数据率;反过来,从节能与共存的角度,也可以在较低功率下维持一定吞吐,从而减少对其他系统的干扰并延长电池寿命。对定位系统而言,这个论点的"侧面价值"是:UWB 的定位并不需要高功率,它更依赖时间分辨率(带宽)与处理增益(前导长度/相关累积)。
4. UWB 定位应用与标准化:为什么 IEEE 802.15.4a 把"测距能力"做成可选项
论文列举了 UWB WSN 的典型应用:医疗(体域网/病人跟踪)、安防与军事(人员授权与追踪)、库存管理(资产实时定位)、搜救(灾害/矿井/消防)、智能家居等,并指出不少场景希望达到"1 英尺以内"的精度,这使 UWB 成为很独特的候选。随后作者概述 IEEE 802.15.4a(2007 批准)作为 802.15.4 的增补,提供 UWB 与 CSS 两种可选 PHY,其中 UWB 选项带有可选的 ranging 能力,并支持若干频段(文中给出 250--750 MHz、3.244--4.742 GHz、5.944--10.234 GHz 等)。
5. 定位体系结构:直接定位 vs 两步定位(Fig.4)
定位系统通常涉及"目标节点"与若干"参考节点"之间的信号交换;位置既可由目标自算(self-positioning),也可由网络侧集中估计(remote/network-centric)。在估计算法结构上,论文强调两类:直接定位与两步定位。
图 4:两步定位多了一个"参数估计层",它不是多余,而是工程可实现性的代价
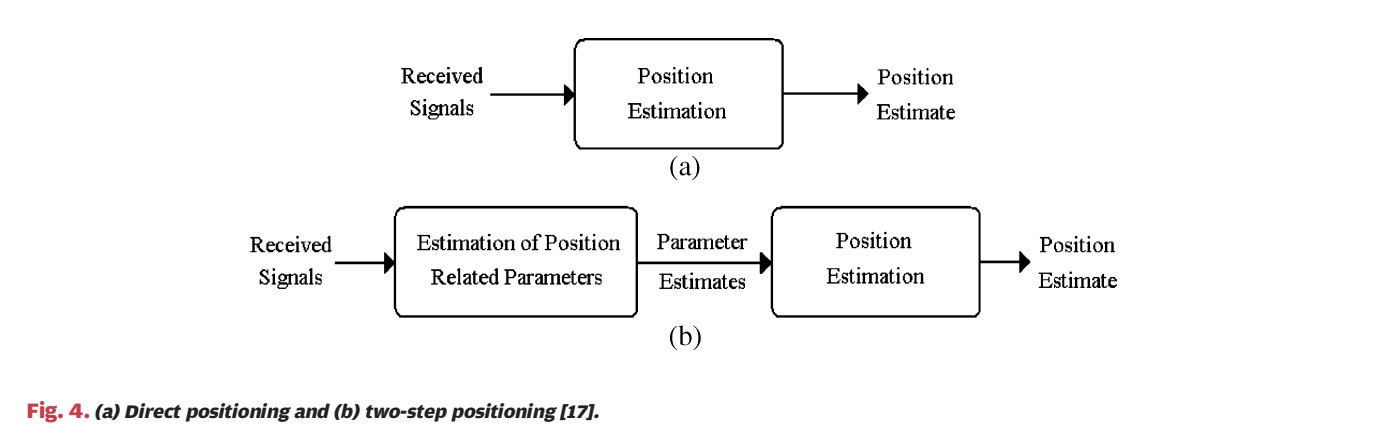
图 4(a) 只有一块:Received Signals → Position Estimation → Position Estimate,代表直接从原始接收波形推断坐标。图 4(b) 则是 Received Signals → Estimation of Position Related Parameters → Parameter Estimates → Position Estimation → Position Estimate,代表先把波形压缩成少量"位置相关参数"(RSS、AOA、TOA...),再用几何/统计方法融合成坐标。
作者的关键判断是:两步法一般是次优的(因为压缩会丢信息),但当信号带宽很高或 SNR 足够高时,两者性能常常很接近;而两步法复杂度显著更低,所以现实系统多采用两步法。UWB 恰恰属于"带宽很高"的一类,因此两步法尤其自然。
6. 第一步:位置相关参数估计(RSS、AOA、TOA、TDOA...)
这一节是整篇的"理论核心",因为作者用一组 CRLB 把可达精度与系统物理量(β\betaβ、SNR、阵列规模等)绑定起来。
6.1 RSS:从路径损耗模型到测距 CRLB(式 (6)--(9))
作者先给出常见的对数距离路径损耗模型(dB 域):
P‾(d)=P0−10nlog10(d/d0)(6) \overline{P}(d)=P_0-10n\log_{10}(d/d_0) \tag{6} P(d)=P0−10nlog10(d/d0)(6)
这里 nnn 是 path-loss exponent,P0P_0P0 是参考距离 d0d_0d0 处的平均接收功率(dB)。实际 RSS 会因反射/散射/绕射产生波动,为减弱小尺度快衰落,接收端可在时域上对功率积分平均:
P(d)=1T∫0T∣r(t;d)∣2 dt(7) P(d)=\frac{1}{T}\int_0^T |r(t;d)|^2\,dt \tag{7} P(d)=T1∫0T∣r(t;d)∣2dt(7)
即便如此仍会受到"阴影衰落"(遮挡等导致的慢变偏差)影响,论文在对数域把它建模为高斯(log-normal shadowing 的常见近似):
P(d)∼N(P‾(d),σsh2)(8) P(d)\sim\mathcal{N}\bigl(\overline{P}(d),\sigma_{\mathrm{sh}}^2\bigr) \tag{8} P(d)∼N(P(d),σsh2)(8)
在这个模型下,作者给出无偏距离估计 d^\hat dd^ 的 CRLB(标准差形式):
Var(d^)≥ln(10) σsh d10n(9) \sqrt{\mathrm{Var}(\hat d)} \ge \frac{\ln(10)\,\sigma_{\mathrm{sh}}\,d}{10n} \tag{9} Var(d^) ≥10nln(10)σshd(9)
这条式子的"读法"是:RSS 测距误差下界随距离 ddd 线性变差 ,与阴影方差 σsh\sigma_{\mathrm{sh}}σsh 成正比、与路径损耗指数 nnn 成反比。论文还给了一个很具体的数值例子:在 IEEE 802.15.4a 的 NLOS residential 信道模型下,若 n=4.58n=4.58n=4.58、σsh=3.51\sigma_{\mathrm{sh}}=3.51σsh=3.51,则 d=10 md=10\ \mathrm{m}d=10 m 时 (9) 给出的下界约 1.76 m1.76\ \mathrm{m}1.76 m,这直接说明 RSS 在复杂 NLOS 场景下很难做到"高精度测距"。
6.2 AOA:角度信息来自"阵列时间差",UWB 让时间差更易估(式 (10))
图 5:AOA 给出的不是"一个点",而是"一个方向约束"
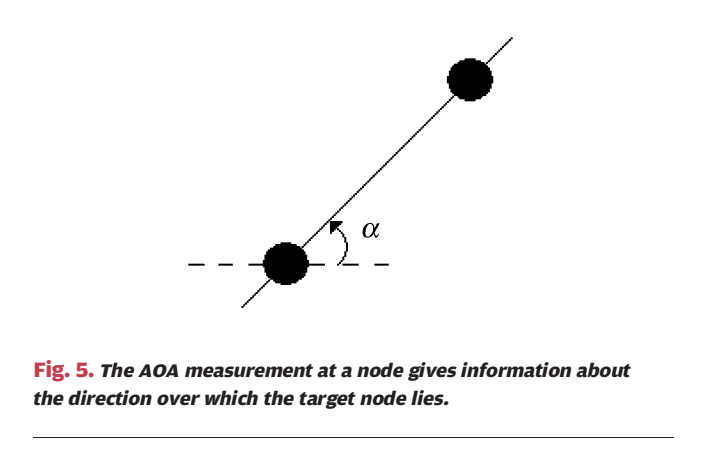
图 5 中下方节点测得入射方向与参考水平线的夹角 α\alphaα,于是目标只能在该方向的射线上。这是 AOA 的基本几何意义:单个角度不足以唯一定位(二维至少两角交会),但它能提供强约束,尤其当距离信息不可靠时。
图 6:ULA 的核心是把角度变成"相邻阵元到达时间差"
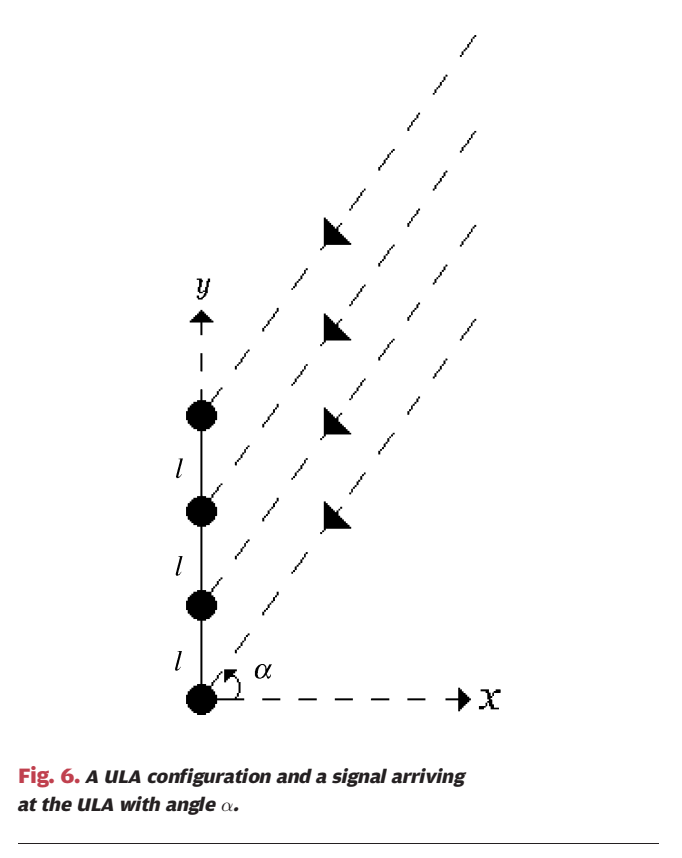
图 6 左侧是一列阵元沿 yyy 轴排列,相邻间距标为 lll。右侧斜虚线表示入射平面波的波前,黑色三角箭头表示传播方向;角度 α\alphaα 是传播方向与 xxx 轴之间的夹角。由于几何投影,相邻阵元的路径差为 lsinαl\sin\alphalsinα,因此相邻阵元的到达时间差为
Δτ=lsinαc \Delta\tau=\frac{l\sin\alpha}{c} Δτ=clsinα
其中 ccc 为光速。论文特别强调:在窄带系统中,时间延迟常可近似等效为"单一相位移",可以用相位扫描做 AOA;但在 UWB 中,一个延迟对应的相位随频率变化,无法用一个相位代表,因此必须显式处理"波形的时间平移"。换句话说,UWB 的 AOA 本质上更像"多通道 TOA/时延差估计问题"。
式 (10):AOA 的 CRLB 把 β\betaβ(有效带宽)写进了分母
作者给出在单径到达、ULA 有 NaN_aNa 个阵元、各阵元 SNR 相同的条件下,无偏 AOA 估计 α^\hat\alphaα^ 的 CRLB(标准差形式):
Var(α^)≥3 c2 π β SNR Na(Na2−1) lcosα(10) \sqrt{\mathrm{Var}(\hat\alpha)} \ge \frac{\sqrt{3}\,c} {\sqrt{2}\,\pi\,\beta\,\sqrt{\mathrm{SNR}}\, \sqrt{N_a(N_a^2-1)}\,l\cos\alpha} \tag{10} Var(α^) ≥2 πβSNR Na(Na2−1) lcosα3 c(10)
其中,β\betaβ 与 SNR\sqrt{\mathrm{SNR}}SNR 越大,角度越准;阵列越长(NaN_aNa 越多、lll 越大)越准;当 α\alphaα 接近 ±90∘\pm 90^\circ±90∘ 时 cosα→0\cos\alpha\to 0cosα→0,角度对时间差的敏感度下降,因此误差下界上升。论文还指出一个与 RSS 对比很关键的点:AOA 的精度随 β\betaβ 线性提升,这意味着 UWB 的大带宽不仅利于 TOA,也能明显利于 AOA。
(附录 D 将把 (10) 从"阵列各通道 TOA Fisher 信息"与"消去未知公共时延 τ0\tau_0τ0"的 Schur complement 推到一致的系数,原文引用文献但未推导。)
6.3 TOA:UWB 定位的绝对主角(式 (11)--(13))
TOA 测距要避免"绝对时钟未知"的歧义,节点要么共享时钟,要么采用两次往返测距协议(two-way ranging)交换时序信息。
在最基本的单径 AWGN 模型下:
r(t)=s(t−τ)+n(t)(11) r(t)=s(t-\tau)+n(t) \tag{11} r(t)=s(t−τ)+n(t)(11)
τ\tauτ 是到达时间(TOA)。相关器用不同候选延迟 τ^\hat\tauτ^ 的模板去相关,取相关峰对应的延迟作为估计:
τ^TOA=argmaxτ^∫r(t) s(t−τ^) dt(12) \hat\tau_{\mathrm{TOA}}=\arg\max_{\hat\tau}\int r(t)\,s(t-\hat\tau)\,dt \tag{12} τ^TOA=argτ^max∫r(t)s(t−τ^)dt(12)
文中解释相关器与匹配滤波器在该模型下是最优的(渐近达到 CRLB),但现实多径会破坏"相关峰=真实 TOA"的简单对应。
图 7:多径下"最大峰值可能不是首径",TOA 会被系统性拉晚
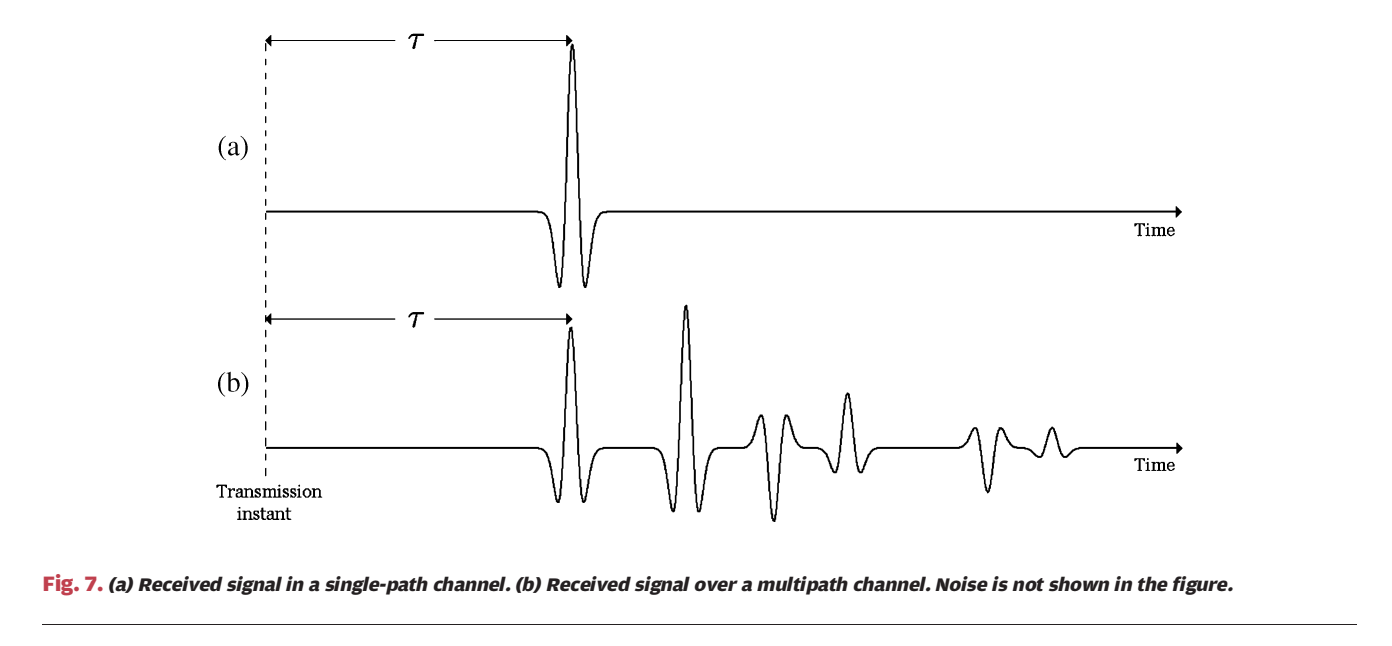
图 7(a) 画的是单径接收:从"Transmission instant"(左侧虚线处)到达一个主要脉冲,图上用箭头标注其延迟 τ\tauτ。图 7(b) 则画出多径:在首径之后出现多组反射/散射脉冲,其中某些后续分量可能幅度更大。若仍用 (12) 的"最大相关峰"做 TOA,极可能选到较强但更晚的路径,导致距离估计偏大。论文因此强调 UWB 场景里常见的 first-path detection(首径检测):目标不是找最大峰,而是尽可能找"最早可可靠检测到的路径"。
式 (13):TOA 的 CRLB = (22πβSNR)−1\bigl(2\sqrt2\pi\beta\sqrt{\mathrm{SNR}}\bigr)^{-1}(22 πβSNR )−1
论文给出 (11) 模型下 TOA 无偏估计的 CRLB(标准差):
Var(τ^)≥122 π β SNR(13) \sqrt{\mathrm{Var}(\hat\tau)} \ge \frac{1}{2\sqrt{2}\,\pi\,\beta\,\sqrt{\mathrm{SNR}}} \tag{13} Var(τ^) ≥22 πβSNR 1(13)
作者随后用一个直观例子强调 UWB 的威力:对"高斯脉冲的二阶导数"且脉冲宽度约 1 ns,在 SNR=5 dB 时,将 TOA 误差换算为距离误差(乘以 ccc)后,下界可小于 1 cm。该例子本质上是在说:当 β\betaβ 达到 GHz 量级时,(13) 的分母巨大,时间估计下界自然压到皮秒--十皮秒量级,换算距离就是毫米--厘米级。
6.4 TDOA:用差分抵消目标端时钟偏置(式 (14))
TDOA 是两个参考节点接收同一信号的到达时间差。只要参考节点之间同步,就可以把目标端未知的时钟偏置在差分里消去:若分别得到两条 TOA,再相减即可;或者直接做互相关估计时延差:
$$
\hat\tau_{\mathrm{TDOA}}
\arg\max_{\tau}
\int_0^{T} r_1(t),r_2(t+\tau),dt
\tag{14}
这条式子从处理角度可以理解为:把两路接收波形在时间轴上滑动对齐,使相似度最大的位置就是 TDOA。 *** ** * ** *** ### 6.5 复合参数与 CIR/PDP:当"单个标量参数"不够时,用更丰富的信道指纹 论文还提到混合方案(TOA/AOA、TOA/RSS、TDOA/AOA、TOA/TDOA 等)以及利用多径功率延迟谱(PDP)或信道冲激响应(CIR)作为"位置指纹"的思路:TOA 只把目标限制在一个圆上,而在某些环境里 CIR 形状在空间上更独特,理论上可直接映射到位置;但代价是需要训练数据库且估计复杂度更高。 *** ** * ** *** ## 7. 第二步:由参数到位置(几何、统计、映射) 论文把第二步分成三类:几何/统计(不依赖训练数据库)与 mapping/fingerprinting(依赖训练数据库)。这三类并不是互斥的,更多是"模型驱动"到"数据驱动"的连续谱。 *** ** * ** *** ### 7.1 几何定位:圆、直线、双曲线(Fig.8--Fig.10) #### 图 8:TOA/RSS 的距离约束是"圆",三圆交点给二维位置 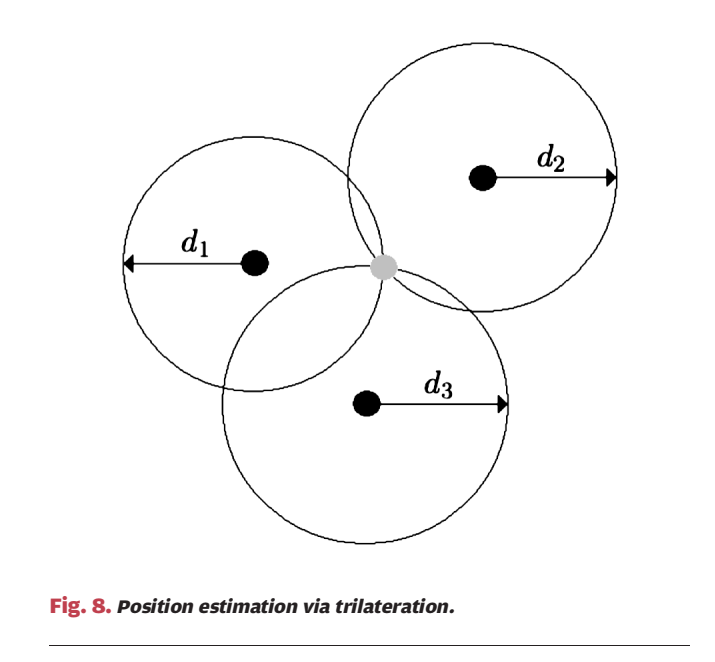 图 8 里三个黑点是参考节点,圆半径标成 d1,d2,d3d_1,d_2,d_3d1,d2,d3,灰点是目标位置。每个测距结果都对应一个圆: (x−xi)2+(y−yi)2=di2,i=1,2,3 (x-x_i)\^2+(y-y_i)\^2=d_i\^2,\\quad i=1,2,3 (x−xi)2+(y−yi)2=di2,i=1,2,3 理想无噪声下三圆共点,解就是目标坐标。这就是 trilateration 的几何直觉。 #### 图 9:AOA 的方向约束是"射线",两射线交会即可定位 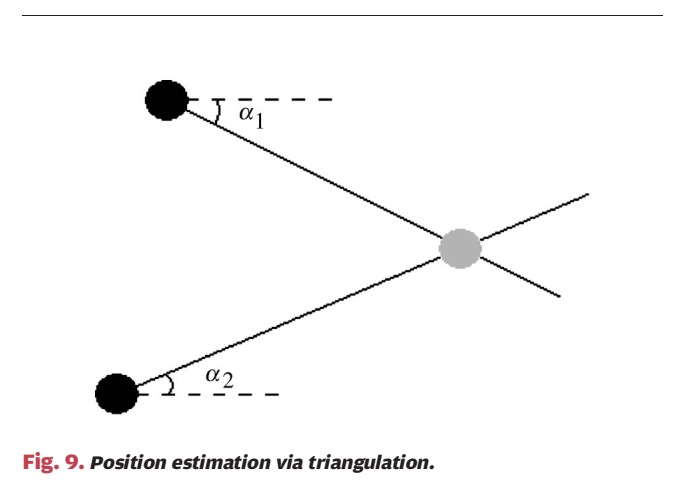 图 9 中两参考节点分别测得角度 α1,α2\\alpha_1,\\alpha_2α1,α2,于是各自产生一条指向目标的直线(或射线),交点处(灰点)即目标位置。 #### 图 10:TDOA 的几何轨迹是"双曲线",两条双曲线交点定位 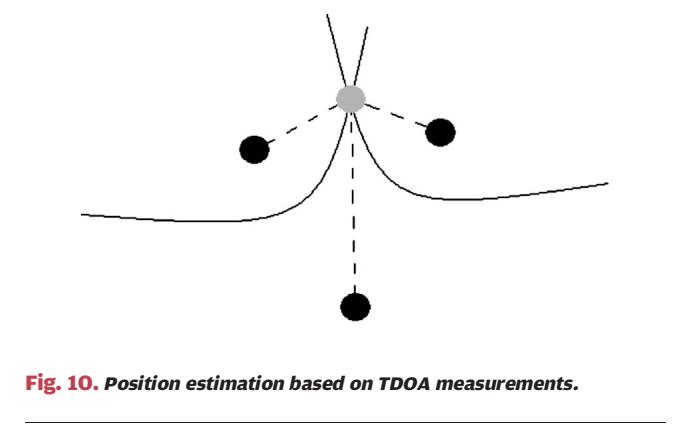 图 10 中底部黑点可视为参考节点 000,左右黑点是参考节点 1,21,21,2。与节点 0 的距离差约束 ∥p−pi∥−∥p−p0∥=Δi\\\|p-p_i\\\|-\\\|p-p_0\\\|=\\Delta_i∥p−pi∥−∥p−p0∥=Δi 形成双曲线,两条双曲线交会于灰点给出目标位置。论文提醒:TDOA 可能存在几何条件不良导致的非唯一解,这与节点布局有关。 ### 7.2 图 11:噪声一来,"交点"变成"交叉区域",几何法缺乏系统融合规则 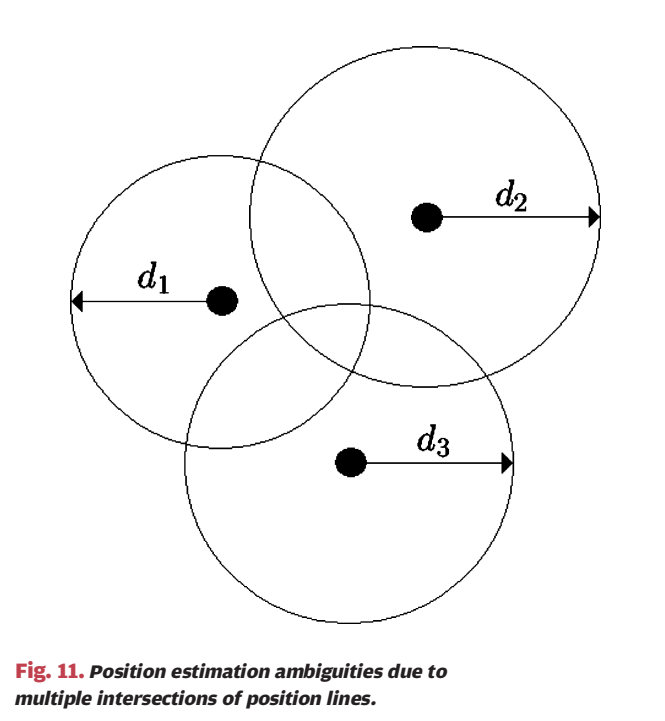 图 11 仍然画了三个圆(对应三次测距),但由于测量带噪,圆不再在单点精确相交,交叉区域出现多个可能交点或干脆无公共交点。几何法在无噪声时非常直观,但在有噪声时缺少一个"最合理的选择原则",也缺少一种自然的"多测量融合机制"。 *** ** * ** *** ### 7.3 统计建模:把问题写成 zi=fi(x,y)+ηiz_i=f_i(x,y)+\\eta_izi=fi(x,y)+ηi(式 (15)--(17)) 为系统处理噪声与融合多测量,作者给出统一观测模型: zi=fi(x,y)+ηi,i=1,...,Nm(15) z_i=f_i(x,y)+\\eta_i,\\quad i=1,\\dots,N_m \\tag{15} zi=fi(x,y)+ηi,i=1,...,Nm(15) 其中 ziz_izi 是测得的参数(通常把时间乘以 ccc 换成距离来统一量纲),fi(x,y)f_i(x,y)fi(x,y) 是在位置 (x,y)(x,y)(x,y) 下的"真值函数",ηi\\eta_iηi 是测量噪声。不同参数类型的 fif_ifi 在文中写为: fi(x,y)={(x−xi)2+(y−yi)2,TOA/RSStan−1 (y−yix−xi),AOA(x−xi)2+(y−yi)2−(x−x0)2+(y−y0)2,TDOA(16) f_i(x,y)= \\begin{cases} \\sqrt{(x-x_i)\^2+(y-y_i)\^2}, \& \\text{TOA/RSS}\\\\\[4pt\] \\tan\^{-1}\\!\\left(\\dfrac{y-y_i}{x-x_i}\\right), \& \\text{AOA}\\\\\[8pt\] \\sqrt{(x-x_i)\^2+(y-y_i)\^2}-\\sqrt{(x-x_0)\^2+(y-y_0)\^2}, \& \\text{TDOA} \\end{cases} \\tag{16} fi(x,y)=⎩ ⎨ ⎧(x−xi)2+(y−yi)2 ,tan−1(x−xiy−yi),(x−xi)2+(y−yi)2 −(x−x0)2+(y−y0)2 ,TOA/RSSAOATDOA(16) 向量形式: z=f(x,y)+η(17) \\mathbf z=\\mathbf f(x,y)+\\boldsymbol\\eta \\tag{17} z=f(x,y)+η(17) 作者进一步把统计方法分为 parametric 与 nonparametric:前者假设噪声 pdf 形式已知(可能带未知参数),后者不假设 pdf 形式,只利用一些一般性质(如方差、对称性)或直接用训练数据驱动。 *** ** * ** *** ### 7.4 Bayes 与 ML:式 (18)--(21) 给出统一的"该优化什么"的答案 设未知参数向量为 Θ=\[x y ΛT\]T \\Theta=\[x\\ \\ y\\ \\ \\Lambda\^T\]\^T Θ=\[x y ΛT\]T 其中 Λ\\LambdaΛ 表示噪声分布可能的未知参数(方差、偏置等)。若存在先验 π(Θ)\\pi(\\Theta)π(Θ),常见贝叶斯估计包括 MMSE 与 MAP: Θ\^MMSE=E{Θ∣z}(18) \\hat\\Theta_{\\mathrm{MMSE}}=\\mathbb E\\{\\Theta\|\\mathbf z\\} \\tag{18} Θ\^MMSE=E{Θ∣z}(18) Θ\^MAP=argmaxΘp(z∣Θ) π(Θ)(19) \\hat\\Theta_{\\mathrm{MAP}}=\\arg\\max_{\\Theta} p(\\mathbf z\|\\Theta)\\,\\pi(\\Theta) \\tag{19} Θ\^MAP=argΘmaxp(z∣Θ)π(Θ)(19) 若无先验,则 ML: Θ\^ML=argmaxΘp(z∣Θ)(20) \\hat\\Theta_{\\mathrm{ML}}=\\arg\\max_{\\Theta} p(\\mathbf z\|\\Theta) \\tag{20} Θ\^ML=argΘmaxp(z∣Θ)(20) 并用"噪声 pdf"写似然: p(z∣Θ)=pη(z−f(x,y) ∣ Θ)(21) p(\\mathbf z\|\\Theta)=p_{\\boldsymbol\\eta}(\\mathbf z-\\mathbf f(x,y)\\,\|\\,\\Theta) \\tag{21} p(z∣Θ)=pη(z−f(x,y)∣Θ)(21) 一旦噪声模型确定,目标函数就确定。 *** ** * ** *** ### 7.5 高斯独立噪声下的 NLS:式 (22)--(25) 把融合写成加权最小二乘 论文给出一个代表性推导(Example 1)。若噪声分量独立: p(z∣Θ)=∏i=1Nmpηi(zi−fi(x,y))(22) p(\\mathbf z\|\\Theta)=\\prod_{i=1}\^{N_m} p_{\\eta_i}\\bigl(z_i-f_i(x,y)\\bigr) \\tag{22} p(z∣Θ)=i=1∏Nmpηi(zi−fi(x,y))(22) 若每个噪声是零均值高斯且方差已知: pηi(n)=12πσiexp (−n22σi2)(23) p_{\\eta_i}(n)=\\frac{1}{\\sqrt{2\\pi}\\sigma_i}\\exp\\!\\left(-\\frac{n\^2}{2\\sigma_i\^2}\\right) \\tag{23} pηi(n)=2π σi1exp(−2σi2n2)(23) 代入得: p(z∣Θ)∝exp (−∑i=1Nm(zi−fi(x,y))22σi2)(24) p(\\mathbf z\|\\Theta) \\propto \\exp\\!\\left( -\\sum_{i=1}\^{N_m}\\frac{(z_i-f_i(x,y))\^2}{2\\sigma_i\^2} \\right) \\tag{24} p(z∣Θ)∝exp(−i=1∑Nm2σi2(zi−fi(x,y))2)(24) 因此 ML 等价于最小化加权残差平方和: ##
\hat{\mathbf Q}_{\mathrm{ML}}
\arg\min_{[x\ y]^T}
\sum_{i=1}{N_m}\frac{(z_i-f_i(x,y))2}{\sigma_i^2}
\tag{25}
其中常用解法包括梯度下降、以及泰勒展开线性化的迭代方法。并特别提醒:TDOA 的噪声往往相关(因为都相对同一个参考节点),因此不能简单用"独立噪声"的 (22),而应回到更一般的 (21)。 (附录 E、F 将把 (25) 的 Gauss--Newton 线性化迭代与"相关高斯噪声→协方差加权二次型"补全,这在原文只一笔带过。) *** ** * ** *** ### 7.6 指纹/映射:用训练数据把 NLOS 与复杂多径"吸收进模型"里(式 (26)(27)) mapping 方法依赖离线训练集: T={(m1,l1),...,(mNT,lNT)}(26) \\mathcal T=\\{(\\mathbf m_1,\\mathbf l_1),\\dots,(\\mathbf m_{N_T},\\mathbf l_{N_T})\\} \\tag{26} T={(m1,l1),...,(mNT,lNT)}(26) 其中 mi\\mathbf m_imi 是测量向量(RSS/TOA/CIR 特征等),li=\[xi yi\]T\\mathbf l_i=\[x_i\\ y_i\]\^Tli=\[xi yi\]T 是位置。k-NN 的在线估计是对最近的 kkk 个训练点位置加权平均: l\^=∑i=1kwi(m) l(i)(27) \\hat{\\mathbf l}=\\sum_{i=1}\^k w_i(\\mathbf m)\\,\\mathbf l_{(i)} \\tag{27} l\^=i=1∑kwi(m)l(i)(27) 作者认为 mapping 在矿井等极端多径/NLOS 环境下可能更稳,因为解析测量模型不可靠时,数据驱动能更鲁棒;但其成本是训练集必须足够大且要随环境变化更新,否则会失效。 *** ** * ** *** ## 8. 为什么第三节专讲 TOA ranging:UWB 的"高精度优势"主要在时间类参数上 作者在第三节开头就做了取舍解释:两步定位的精度取决于第一步参数估计精度。UWB 的高时间分辨率使 T(D)OA、AOA 都可以更精确,但 RSS 即便在 UWB 中也仍很粗;AOA 又常需要阵列、复杂度较高。因此工程上更偏向 TOA(以及 TDOA)来做 UWB 定位。 *** ** * ** *** ## 9. 时间测距的四类主要误差来源:多径、MAI、NLOS、高时间分辨率带来的实现挑战 ### 9.1 多径:UWB 能"分辨多径",但首径检测仍是核心 窄带系统的脉冲宽、各径时延差相对小,多径叠加导致相关峰偏移,需要超分辨率时延估计算法;而 UWB 的脉冲窄、分辨率高,多径往往可分辨,相关法不必依赖超分辨率即可较准。但即便可分辨,多径仍会导致"最大峰非首径"的风险,所以首径检测仍关键。作者也强调分析多径影响需要准确的 UWB 信道模型,IEEE 802.15.4a 信道模型提供了各径时延与幅度的统计信息,可据此对 TOA 误差建模。 *** ** * ** *** ### 9.2 多址干扰 MAI:网络并发会让 TOA 退化,需要时频分配与抑制技术 作者提到常用 MAI 缓解包括给用户分配不同时间槽或频段,但仍可能存在网络间干扰,因此会用非线性滤波、训练序列设计等方法降低干扰对 TOA 的破坏。 *** ** * ** *** ### 9.3 NLOS:最棘手的不是方差,而是"正偏差(bias)" 当 LOS 被遮挡,直达径可能被强烈衰减甚至不可检测。如果只是衰减但仍可检测,首径检测还有希望;如果直达径不可检测,则"最早可检测径"比真实 TOA 晚,产生正偏差,称为 NLOS error。论文认为 NLOS 误差缓解是高精度 TOA 里最具挑战的任务之一,并给出三条路线: 其一,mapping 技术因训练集隐含了 NLOS 的影响而更鲁棒;其二,若已知 NLOS 统计特性,可做 NLOS 识别与修正(例如利用 NLOS 时 TOA 方差往往更大来识别);其三,基于散射模型得到 TOA 统计后,用 MAP/ML 做补偿。 *** ** * ** *** ### 9.4 高时间分辨率的"副作用":时钟抖动、难以奈奎斯特采样、搜索空间巨大 作者强调四个现实问题: 第一,UWB 脉冲极短,时钟 jitter 与漂移会显著影响 TOA;第二,UWB 的奈奎斯特采样率通常是数 GHz,功耗与实现难度极高,因此希望用低采样率信息;第三,时间分辨率高意味着可能的延迟栅格极密,串行相关搜索会非常慢;因此需要快速 TOA 搜索算法与两阶段方案。 *** ** * ** *** ## 10. TOA ranging 算法:从相关找峰到快速搜索与两阶段估计(Fig.12) ### 图 12:相关式 TOA 接收机是一个"模板--相关--判决--延迟更新"的闭环 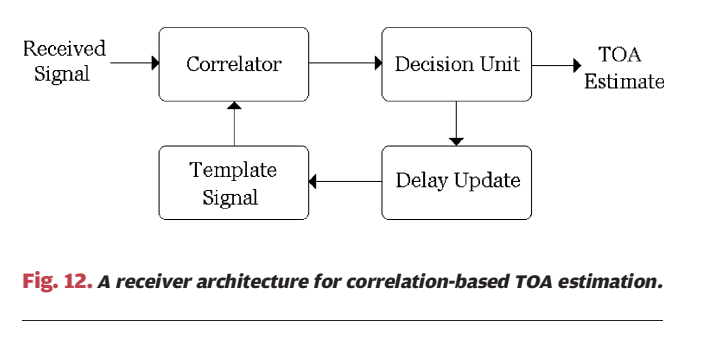 图 12 的信号流是:Received Signal → Correlator → Decision Unit → TOA Estimate。Template Signal 同时输入 Correlator。Decision Unit 的输出还反馈到 Delay Update,Delay Update 再驱动 Template Signal(本质是更新模板延迟 τ\^\\hat\\tauτ\^ 的候选值)。这张框图把"搜索"的本质画得很直白:相关器本身不决定测哪个延迟点,延迟更新策略才决定复杂度与速度。 论文讨论了几类策略:传统的串行搜索会寻找第一个超过阈值的相关输出(而不是最大峰),但仍可能耗时很长;为加速可用随机搜索或 bit reversal search 等;更通用的工程方案是"两步法":先用低复杂度方法(如能量检测器)快速得到粗 TOA 区间,再在小区间内用相关首径检测或统计变化检测做精估计。作者还强调低功耗实现往往依赖低采样率的 TOA 估计器,包括能量检测(非相干)、低速相关输出、符号率自相关接收机等。 *** ** * ** *** ## 11. 实用设计:信号设计与硬件实现(第四节 + Fig.13--Fig.14) ### 11.1 精度指标:RMSE(式 (28)(29))把"偏差+方差"都算进去 测距精度常用指标 RMSE: RMSE=E\[(d\^−d)2\](28) \\mathrm{RMSE}=\\sqrt{\\mathbb E\[(\\hat d-d)\^2\]} \\tag{28} RMSE=E\[(d\^−d)2\] (28) 实验/仿真中用样本均值近似: RMSE≈1N∑i=1N(d\^i−di)2(29) \\mathrm{RMSE}\\approx \\sqrt{\\frac{1}{N}\\sum_{i=1}\^{N}(\\hat d_i-d_i)\^2} \\tag{29} RMSE≈N1i=1∑N(d\^i−di)2 (29) 这里 d\^\\hat dd\^ 是距离估计,ddd 是真值。RMSE 与 CRLB 的关系是:CRLB更多是"模型正确且无偏时的理论方差下界",RMSE 则把偏差也算进来,因此在 NLOS 等有偏场景下 RMSE 才是更真实的性能刻画。 *** ** * ** *** ### 11.2 测距信号结构:式 (30) 把 Fig.3 的脉冲列写成可分析的形式 作者采用 Fig.3 的泛化结构: s(t)=∑j=1∞aj ω(t−jTf)(30) s(t)=\\sum_{j=1}\^{\\infty} a_j\\,\\omega(t-jT_f) \\tag{30} s(t)=j=1∑∞ajω(t−jTf)(30) 其中 ω(t)\\omega(t)ω(t) 是 UWB 脉冲,TfT_fTf 是帧间隔,aja_jaj 是二元 {±1}\\{\\pm 1\\}{±1} 或三元 {−1,0,+1}\\{-1,0,+1\\}{−1,0,+1} 码,用于抗干扰与谱优化。论文举 IEEE 802.15.4a 的例子:同步前导采用三元码并用于 ranging。 在 FCC 平均 PSD 约束下,论文指出可由掩膜确定可发的最大平均功率 PmaxP_{\\max}Pmax;则每一帧可用能量量级为 TfPmaxT_f P_{\\max}TfPmax。如果测距信号包含 NfN_fNf 个脉冲(总时长 T=NfTfT=N_fT_fT=NfTf),则 (13) 里的 SNR\\mathrm{SNR}SNR 会与 TPmaxT P_{\\max}TPmax 成正比,因此测距时长越长,CRLB 越低(误差方差与 TTT 近似成反比)。 这一段在原文是"口头说明",附录 G 将把它更明确地写成能量/SNR 的关系链,并解释为什么 TfT_fTf 既不能太大也不能太小(峰值功率上限 vs 多径帧间干扰)。 *** ** * ** *** ### 11.3 发射机实现:把通信与测距前导放进同一个 packet(Fig.13) 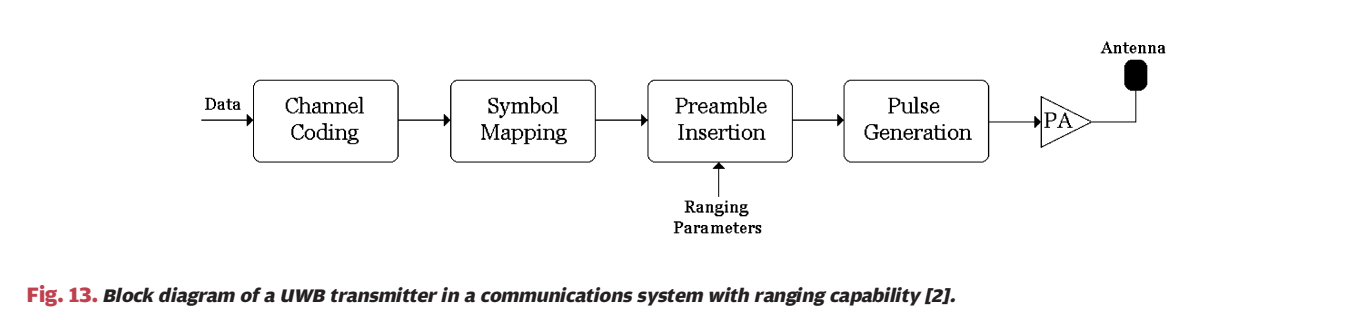 图 13 是一个"通信+测距"一体的典型发射链:Data → Channel Coding → Symbol Mapping → Preamble Insertion → Pulse Generation →(可选)PA → Antenna。Preamble insertion 模块把测距/同步相关的前导插在数据前面,前导既用于 ranging,也常用于捕获、同步、信道估计等。 作者对 UWB 脉冲发生器做了两类划分:一类先在基带生成再上变频到目标中心频带;另一类直接在目标频带生成(例如用高斯脉冲导数、用天线整形、用滤波整形等)。关于 PA,论文指出在极低功率法规下甚至可以不需要 PA;但在需要 PA 的场景里,效率(输出到负载的信号功率与放大器总耗电之比)对功耗至关重要。 *** ** * ** *** ### 11.4 天线:UWB 的硬件难点常常是"宽带一致性"而不是某一单点性能 论文强调 UWB 天线需要宽阻抗带宽(将失配损耗限制在 10%以内),并且要尽量保证辐射出来的脉冲波形与馈电处的脉冲(或其导数)相似,以免产生严重脉冲畸变;同时由于发射功率受监管限制,天线辐射效率必须高,否则可用距离会显著缩短。作者还提到多种宽带天线结构与带宽拓展技巧,并认为多种平面天线(bowtie、diamond、方形偶极、各类单极子)在 UWB 中较常见,因为它们紧凑、适合 PCB、带宽可做大且畸变可控。 *** ** * ** *** ### 11.5 接收机实现:全数字 vs 模拟相关/能量检测(Fig.14),"ADC"是核心瓶颈 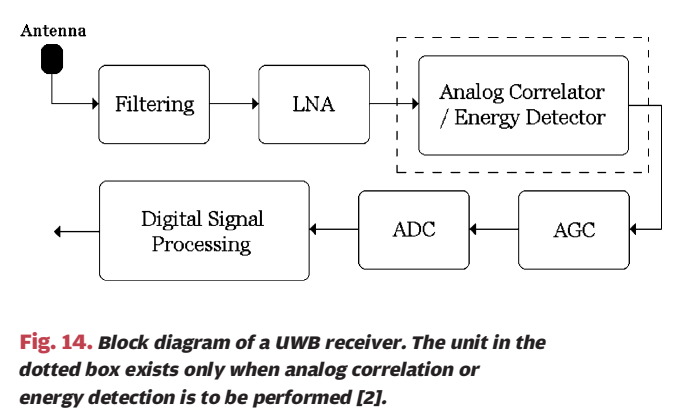 图 14 的主链是:Antenna → Filtering → LNA →(虚线框:Analog Correlator / Energy Detector,可选)→ AGC → ADC → Digital Signal Processing。虚线框表示:只有当系统在模拟域先做相关或能量检测时才需要这块。 论文把接收机分成两类: 第一类是 all-digital:尽早 ADC,把相关等处理放到数字域,灵活性高;但必须面对 GHz 级采样率导致的高功耗与实现难度。第二类是先在模拟域做相关/能量检测,再用低速 ADC(每帧或每符号采一次也许就够),这样功耗更低但更容易受电路失配影响,且相关器数量受限使得一些复杂干扰抑制不易实现。 作者还强调一个很"UWB 工程化"的经验:相比采样率,ADC 的分辨率要求没那么苛刻;超过 4 bit 往往只有边际提升。为满足高采样率要求,常用频域 channelization 或 subsampling 等技术分摊压力。 *** ** * ** *** ## 12. 小结 TOA/AOA 的理论精度由 Fisher 信息控制,而 Fisher 信息在时间延迟问题中几乎总会把信号带宽压缩成一个有效带宽 β\\betaβ;UWB 的价值在于把 β\\betaβ 做到极大,从而把时间估计下界压到很小。但真实系统中,多径(首径检测)、MAI(抑制)、NLOS(偏差建模/识别/校正)、以及实现约束(时钟抖动、ADC 采样、搜索复杂度)会把"理论厘米级"变成"工程上要精心设计才能接近的厘米级"。这也是作者把第三节与第四节写得同样重要的原因。 ## 附录: ### 附录 A:由 (6)(8) 推出 RSS 测距 CRLB (9) 在 dB 域观测模型 (8) 可写成 P=P‾(d)+X,X∼N(0,σsh2) P=\\overline{P}(d)+X,\\quad X\\sim\\mathcal N(0,\\sigma_{\\mathrm{sh}}\^2) P=P(d)+X,X∼N(0,σsh2) 其中 P‾(d)=P0−10nlog10(d/d0) \\overline{P}(d)=P_0-10n\\log_{10}(d/d_0) P(d)=P0−10nlog10(d/d0) 对单次观测、参数为 ddd 的高斯模型,Fisher 信息是 I(d)=1σsh2(dP‾(d)dd)2 \\mathcal I(d)=\\frac{1}{\\sigma_{\\mathrm{sh}}\^2}\\left(\\frac{d\\overline{P}(d)}{dd}\\right)\^2 I(d)=σsh21(dddP(d))2 计算导数。注意 log10(d/d0)=ln(d/d0)ln10⇒dddlog10(d/d0)=1dln10 \\log_{10}(d/d_0)=\\frac{\\ln(d/d_0)}{\\ln 10} \\Rightarrow \\frac{d}{dd}\\log_{10}(d/d_0)=\\frac{1}{d\\ln 10} log10(d/d0)=ln10ln(d/d0)⇒dddlog10(d/d0)=dln101 因此 dP‾(d)dd=−10n⋅1dln10=−10ndln10 \\frac{d\\overline{P}(d)}{dd} =-10n\\cdot\\frac{1}{d\\ln 10} =-\\frac{10n}{d\\ln 10} dddP(d)=−10n⋅dln101=−dln1010n 代回 Fisher 信息: I(d)=1σsh2(10ndln10)2 \\mathcal I(d) =\\frac{1}{\\sigma_{\\mathrm{sh}}\^2} \\left(\\frac{10n}{d\\ln 10}\\right)\^2 I(d)=σsh21(dln1010n)2 CRLB: ##
\mathrm{Var}(\hat d)\ge \frac{1}{\mathcal I(d)}
\sigma_{\mathrm{sh}}^2\left(\frac{d\ln 10}{10n}\right)^2
两边开方得到: Var(d\^)≥ln(10) σsh d10n \\sqrt{\\mathrm{Var}(\\hat d)} \\ge \\frac{\\ln(10)\\,\\sigma_{\\mathrm{sh}}\\,d}{10n} Var(d\^) ≥10nln(10)σshd 即式 (9)。这也解释了为什么 RSS 的测距误差下界随 ddd 线性恶化:因为均值函数对 ddd 的导数本身是 1/d1/d1/d 级别。 *** ** * ** *** ### 附录 B:为什么相关器/匹配滤波在 (11) 模型下等价于 ML(推到 (12)) 模型 (11): r(t)=s(t−τ)+n(t) r(t)=s(t-\\tau)+n(t) r(t)=s(t−τ)+n(t) 设噪声为零均值白高斯,双边功率谱密度 N0/2N_0/2N0/2。在连续时间高斯噪声下,给定 τ\\tauτ 的对数似然(忽略常数)与平方误差泛函成反比: ##
\ln p(r|\tau)
-\frac{1}{N_0}\int \bigl(r(t)-s(t-\tau)\bigr)^2 dt + \text{const}
最大化 lnp(r∣τ)\\ln p(r\|\\tau)lnp(r∣τ) 等价于最小化 J(τ)=∫(r(t)−s(t−τ))2dt J(\\tau)=\\int \\bigl(r(t)-s(t-\\tau)\\bigr)\^2 dt J(τ)=∫(r(t)−s(t−τ))2dt 展开: J(τ)=∫r2(t) dt−2∫r(t)s(t−τ) dt+∫s2(t−τ) dt J(\\tau)=\\int r\^2(t)\\,dt -2\\int r(t)s(t-\\tau)\\,dt + \\int s\^2(t-\\tau)\\,dt J(τ)=∫r2(t)dt−2∫r(t)s(t−τ)dt+∫s2(t−τ)dt 其中 ∫r2(t) dt\\int r\^2(t)\\,dt∫r2(t)dt 与 τ\\tauτ 无关;若 sss 能量有限且与平移无关,则 ∫s2(t−τ) dt=∫s2(t) dt\\int s\^2(t-\\tau)\\,dt=\\int s\^2(t)\\,dt∫s2(t−τ)dt=∫s2(t)dt 也与 τ\\tauτ 无关。于是最小化 J(τ)J(\\tau)J(τ) 等价于最大化互相关项: ##
\hat\tau
\arg\max_{\tau} \int r(t),s(t-\tau),dt
即式 (12)。这就说明:在 (11) 的单径 AWGN 条件下,相关器/匹配滤波的"找峰"就是 ML。 *** ** * ** *** ### 附录 C:TOA CRLB (13) 的完整推导与有效带宽 β\\betaβ 的出现方式 仍在 (11) 模型下。TOA 参数 τ\\tauτ 的 Fisher 信息(连续时间白高斯噪声)为经典结果: I(τ)=2N0∫−∞∞(∂s(t−τ)∂τ)2dt \\mathcal I(\\tau)=\\frac{2}{N_0}\\int_{-\\infty}\^{\\infty} \\left(\\frac{\\partial s(t-\\tau)}{\\partial \\tau}\\right)\^2 dt I(τ)=N02∫−∞∞(∂τ∂s(t−τ))2dt 而 ∂s(t−τ)∂τ=−s′(t−τ) \\frac{\\partial s(t-\\tau)}{\\partial \\tau}=-s'(t-\\tau) ∂τ∂s(t−τ)=−s′(t−τ) 故 ##
\mathcal I(\tau)=\frac{2}{N_0}\int (s'(t-\tau))^2 dt
\frac{2}{N_0}\int (s'(t))^2 dt
将 ∫∣s′(t)∣2dt\\int \|s'(t)\|\^2 dt∫∣s′(t)∣2dt 变换到频域。若 S(f)S(f)S(f) 为 s(t)s(t)s(t) 的傅里叶变换,则 s′(t)s'(t)s′(t) 的频域是 j2πfS(f)j2\\pi f S(f)j2πfS(f),Parseval 定理给出: ∫∣s′(t)∣2dt=∫∣j2πfS(f)∣2df=(2π)2∫f2∣S(f)∣2df \\int \|s'(t)\|\^2 dt =\\int \|j2\\pi f S(f)\|\^2 df =(2\\pi)\^2\\int f\^2 \|S(f)\|\^2 df ∫∣s′(t)∣2dt=∫∣j2πfS(f)∣2df=(2π)2∫f2∣S(f)∣2df 定义信号能量 Es=∫∣s(t)∣2dt=∫∣S(f)∣2df E_s=\\int \|s(t)\|\^2 dt=\\int \|S(f)\|\^2 df Es=∫∣s(t)∣2dt=∫∣S(f)∣2df 定义有效带宽(RMS 带宽): β2=∫f2∣S(f)∣2df∫∣S(f)∣2df=1Es∫f2∣S(f)∣2df \\beta\^2 =\\frac{\\int f\^2 \|S(f)\|\^2 df}{\\int \|S(f)\|\^2 df} =\\frac{1}{E_s}\\int f\^2 \|S(f)\|\^2 df β2=∫∣S(f)∣2df∫f2∣S(f)∣2df=Es1∫f2∣S(f)∣2df 则 ∫∣s′(t)∣2dt=(2π)2β2Es \\int \|s'(t)\|\^2 dt=(2\\pi)\^2\\beta\^2 E_s ∫∣s′(t)∣2dt=(2π)2β2Es 代回 Fisher 信息: I(τ)=2N0(2π)2β2Es=8π2β2EsN0 \\mathcal I(\\tau)=\\frac{2}{N_0}(2\\pi)\^2\\beta\^2 E_s =\\frac{8\\pi\^2\\beta\^2 E_s}{N_0} I(τ)=N02(2π)2β2Es=N08π2β2Es 令 SNR=Es/N0\\mathrm{SNR}=E_s/N_0SNR=Es/N0(与文中常用能量信噪比口径一致),得 I(τ)=8π2β2SNR \\mathcal I(\\tau)=8\\pi\^2\\beta\^2\\mathrm{SNR} I(τ)=8π2β2SNR CRLB: ##
\mathrm{Var}(\hat\tau)\ge \frac{1}{\mathcal I(\tau)}
\frac{1}{8\pi2\beta2\mathrm{SNR}}
开方: Var(τ\^)≥122πβSNR \\sqrt{\\mathrm{Var}(\\hat\\tau)} \\ge \\frac{1}{2\\sqrt{2}\\pi\\beta\\sqrt{\\mathrm{SNR}}} Var(τ\^) ≥22 πβSNR 1 即式 (13)。若要换算距离 d=cτd=c\\taud=cτ,则 Var(d\^)≥c22πβSNR \\sqrt{\\mathrm{Var}(\\hat d)}\\ge \\frac{c}{2\\sqrt{2}\\pi\\beta\\sqrt{\\mathrm{SNR}}} Var(d\^) ≥22 πβSNR c 这就是作者说"UWB 可到厘米级"的数学根。 *** ** * ** *** ### 附录 D:ULA 单径条件下 AOA CRLB (10) 的推导(含消去未知公共时延) 这部分推导的关键是:阵列每个通道都像一个"TOA 观测器",但它们共享一个未知公共延迟 τ0\\tau_0τ0(传播到阵列参考点的整体延迟),角度只体现在"随阵元编号线性增长的相对延迟"上。 设 ULA 有 NaN_aNa 个阵元,编号 m=0,1,...,Na−1m=0,1,\\dots,N_a-1m=0,1,...,Na−1。单径平面波入射角为 α\\alphaα,第 mmm 个阵元的到达时间为 τm(α)=τ0+mlsinαc \\tau_m(\\alpha)=\\tau_0+\\frac{m l\\sin\\alpha}{c} τm(α)=τ0+cmlsinα 其中 lll 为阵元间距。对参数向量 θ=\[τ0,α\]T\\theta=\[\\tau_0,\\alpha\]\^Tθ=\[τ0,α\]T,有 ∂τm∂τ0=1,∂τm∂α=mlcosαc \\frac{\\partial \\tau_m}{\\partial \\tau_0}=1,\\qquad \\frac{\\partial \\tau_m}{\\partial \\alpha}=\\frac{m l\\cos\\alpha}{c} ∂τ0∂τm=1,∂α∂τm=cmlcosα 在每个阵元上,若接收信号满足 (11) 的单径 AWGN 模型,则"单个延迟参数"的 Fisher 信息与附录 C 相同: Iτ=8π2β2SNR \\mathcal I_{\\tau} = 8\\pi\^2\\beta\^2\\mathrm{SNR} Iτ=8π2β2SNR (这里 SNR\\mathrm{SNR}SNR 指每个阵元的信噪比,论文假设所有阵元相同。) 由于各阵元噪声独立,总 Fisher 信息矩阵是各阵元信息累加: I(θ)=∑m=0Na−1Iτ\[∂τm∂τ0∂τm∂α\]\[∂τm∂τ0∂τm∂α\] \\mathbf I(\\theta)= \\sum_{m=0}\^{N_a-1} \\mathcal I_{\\tau} \\begin{bmatrix} \\frac{\\partial \\tau_m}{\\partial \\tau_0}\\\\\[4pt\] \\frac{\\partial \\tau_m}{\\partial \\alpha} \\end{bmatrix} \\begin{bmatrix} \\frac{\\partial \\tau_m}{\\partial \\tau_0}\& \\frac{\\partial \\tau_m}{\\partial \\alpha} \\end{bmatrix} I(θ)=m=0∑Na−1Iτ\[∂τ0∂τm∂α∂τm\]\[∂τ0∂τm∂α∂τm\] 因此 ##
I_{\tau_0\tau_0}
\mathcal I_{\tau}\sum_{m=0}^{N_a-1} 1
\mathcal I_{\tau}N_a
##
I_{\alpha\alpha}
\mathcal I_{\tau}\sum_{m=0}^{N_a-1}\left(\frac{m l\cos\alpha}{c}\right)^2
\mathcal I_{\tau}\left(\frac{l\cos\alpha}{c}\right)2\sum_{m=0}{N_a-1}m^2
##
I_{\tau_0\alpha}
\mathcal I_{\tau}\sum_{m=0}^{N_a-1}
\left(1\cdot\frac{m l\cos\alpha}{c}\right)
\mathcal I_{\tau}\left(\frac{l\cos\alpha}{c}\right)\sum_{m=0}^{N_a-1}m
当 τ0\\tau_0τ0 是 nuisance parameter 时,α\\alphaα 的等效 Fisher 信息是 Schur complement: ##
I_{\mathrm{eff}}(\alpha)
I_{\alpha\alpha}-\frac{I_{\tau_0\alpha}^2}{I_{\tau_0\tau_0}}
把上式代入,可得 ##
I_{\mathrm{eff}}(\alpha)
\mathcal I_{\tau}\left(\frac{l\cos\alpha}{c}\right)^2
\left(
\sum m^2 - \frac{(\sum m)^2}{N_a}
\right)
而 ∑m=0Na−1m=Na(Na−1)2,∑m=0Na−1m2=(Na−1)Na(2Na−1)6 \\sum_{m=0}\^{N_a-1}m=\\frac{N_a(N_a-1)}{2},\\qquad \\sum_{m=0}\^{N_a-1}m\^2=\\frac{(N_a-1)N_a(2N_a-1)}{6} m=0∑Na−1m=2Na(Na−1),m=0∑Na−1m2=6(Na−1)Na(2Na−1) 可化简得到(这一步很关键,它等价于"阵元编号的方差×阵元数"): ##
\sum m^2 - \frac{(\sum m)^2}{N_a}
\frac{N_a(N_a^2-1)}{12}
所以 ##
I_{\mathrm{eff}}(\alpha)
\mathcal I_{\tau}\left(\frac{l\cos\alpha}{c}\right)^2
\frac{N_a(N_a^2-1)}{12}
CRLB: Var(α\^)≥1Ieff(α) \\mathrm{Var}(\\hat\\alpha)\\ge \\frac{1}{I_{\\mathrm{eff}}(\\alpha)} Var(α\^)≥Ieff(α)1 开方: Var(α\^)≥clcosα⋅1Iτ⋅12Na(Na2−1) \\sqrt{\\mathrm{Var}(\\hat\\alpha)} \\ge \\frac{c}{l\\cos\\alpha} \\cdot \\frac{1}{\\sqrt{\\mathcal I_{\\tau}}} \\cdot \\sqrt{\\frac{12}{N_a(N_a\^2-1)}} Var(α\^) ≥lcosαc⋅Iτ 1⋅Na(Na2−1)12 代入 Iτ=8π2β2SNR\\mathcal I_{\\tau}=8\\pi\^2\\beta\^2\\mathrm{SNR}Iτ=8π2β2SNR,得到 Var(α\^)≥clcosα⋅18πβSNR⋅12Na(Na2−1) \\sqrt{\\mathrm{Var}(\\hat\\alpha)} \\ge \\frac{c}{l\\cos\\alpha} \\cdot \\frac{1}{\\sqrt{8}\\pi\\beta\\sqrt{\\mathrm{SNR}}} \\cdot \\sqrt{\\frac{12}{N_a(N_a\^2-1)}} Var(α\^) ≥lcosαc⋅8 πβSNR 1⋅Na(Na2−1)12 ##
\frac{\sqrt{3},c}
{\sqrt{2},\pi,\beta,\sqrt{\mathrm{SNR}},
\sqrt{N_a(N_a^2-1)},l\cos\alpha}
完全一致于式 (10)。这也清晰解释了式 (10) 里那个看似"神秘"的 Na(Na2−1)\\sqrt{N_a(N_a\^2-1)}Na(Na2−1) :它来自阵元编号去均值后的二次和。 *** ** * ** *** ### 附录 E:由 (15)(23) 推出 (25) 后,如何用 Gauss--Newton 线性化求解 式 (25) 是一个非线性加权最小二乘。写成矩阵形式更清晰: ##
\hat{\mathbf q}
\arg\min_{\mathbf q=[x\ y]^T}
\left(\mathbf z-\mathbf f(\mathbf q)\right)^T
\mathbf W
\left(\mathbf z-\mathbf f(\mathbf q)\right)
其中 W=diag(1/σ12,...,1/σNm2)\\mathbf W=\\mathrm{diag}(1/\\sigma_1\^2,\\dots,1/\\sigma_{N_m}\^2)W=diag(1/σ12,...,1/σNm2)。 Gauss--Newton 的核心是对 f(q)\\mathbf f(\\mathbf q)f(q) 在当前迭代点 qk\\mathbf q_kqk 做一阶泰勒展开: f(qk+Δ)≈f(qk)+JkΔ \\mathbf f(\\mathbf q_k+\\Delta) \\approx \\mathbf f(\\mathbf q_k)+\\mathbf J_k\\Delta f(qk+Δ)≈f(qk)+JkΔ Jk\\mathbf J_kJk 是 Jacobian: Jk=∂f∂q∣q=qk \\mathbf J_k=\\left.\\frac{\\partial \\mathbf f}{\\partial \\mathbf q}\\right\|_{\\mathbf q=\\mathbf q_k} Jk=∂q∂f q=qk 把线性化代入目标函数,得到关于 Δ\\DeltaΔ 的二次型最小化,解满足正规方程: ##
(\mathbf J_k^T\mathbf W\mathbf J_k)\Delta
\mathbf J_k^T\mathbf W\left(\mathbf z-\mathbf f(\mathbf q_k)\right)
于是迭代更新: qk+1=qk+Δ \\mathbf q_{k+1}=\\mathbf q_k+\\Delta qk+1=qk+Δ 对于 TOA/RSS 类型的 fi(x,y)=(x−xi)2+(y−yi)2f_i(x,y)=\\sqrt{(x-x_i)\^2+(y-y_i)\^2}fi(x,y)=(x−xi)2+(y−yi)2 ,其偏导数为: ∂fi∂x=x−xi(x−xi)2+(y−yi)2,∂fi∂y=y−yi(x−xi)2+(y−yi)2 \\frac{\\partial f_i}{\\partial x}= \\frac{x-x_i}{\\sqrt{(x-x_i)\^2+(y-y_i)\^2}},\\qquad \\frac{\\partial f_i}{\\partial y}= \\frac{y-y_i}{\\sqrt{(x-x_i)\^2+(y-y_i)\^2}} ∂x∂fi=(x−xi)2+(y−yi)2 x−xi,∂y∂fi=(x−xi)2+(y−yi)2 y−yi 把这些导数填进 Jk\\mathbf J_kJk 就可实现一个标准的"加权迭代最小二乘定位器"。这就是原文提到的"Taylor series linearization techniques"的具体形式。 *** ** * ** *** ### 附录 F:TDOA 噪声相关时,(25) 应如何改写(原文只提示未展开) 作者指出 TDOA 的噪声项往往相关,因为多个 TDOA 都相对同一个参考节点生成,会共享同一参考端 TOA 误差项。此时若仍用 (25) 的"独立噪声对角权重"会不匹配。 若噪声向量 η∼N(0,Σ)\\boldsymbol\\eta\\sim\\mathcal N(\\mathbf 0,\\mathbf\\Sigma)η∼N(0,Σ) 为相关高斯,则 p(z∣q)∝exp (−12(z−f(q))TΣ−1(z−f(q))) p(\\mathbf z\|\\mathbf q) \\propto \\exp\\!\\left( -\\frac{1}{2} (\\mathbf z-\\mathbf f(\\mathbf q))\^T \\mathbf\\Sigma\^{-1} (\\mathbf z-\\mathbf f(\\mathbf q)) \\right) p(z∣q)∝exp(−21(z−f(q))TΣ−1(z−f(q))) 因此 ML 等价于最小化 ##
\hat{\mathbf q}
\arg\min_{\mathbf q}
(\mathbf z-\mathbf f(\mathbf q))^T
\mathbf\Sigma^{-1}
(\mathbf z-\mathbf f(\mathbf q))
这就是"协方差加权"的广义最小二乘(GLS)。其 Gauss--Newton 更新只需把附录 E 的 W\\mathbf WW 换成 Σ−1\\mathbf\\Sigma\^{-1}Σ−1: ##
(\mathbf J_kT\mathbf\Sigma{-1}\mathbf J_k)\Delta
\mathbf J_kT\mathbf\Sigma{-1}\left(\mathbf z-\mathbf f(\mathbf q_k)\right)
这部分推导与结论是理解"为什么 TDOA 系统要特别处理相关性"的关键。 *** ** * ** *** ### 附录 G:式 (30) 与 FCC PSD 约束如何推出"SNR∝TPmax\\mathrm{SNR}\\propto T P_{\\max}SNR∝TPmax"(原文为文字叙述) 原文在第四节给出的逻辑是:FCC 掩膜决定最大平均功率 PmaxP_{\\max}Pmax,从而一帧内最大能量与 TfPmaxT_fP_{\\max}TfPmax 同阶;若有 NfN_fNf 帧,总能量与 NfTfPmax=TPmaxN_fT_fP_{\\max}=TP_{\\max}NfTfPmax=TPmax 同阶,于是 (13) 中 SNR\\mathrm{SNR}SNR 与 TPmaxTP_{\\max}TPmax 成正比,因而误差下界与 TTT 反比。 把这段更公式化地写出来,可这样理解:在平均功率受限为 PmaxP_{\\max}Pmax 的前提下,观测窗口 TTT 内可发送/接收的有效能量上界近似为 Es≲∫0TPmax dt=TPmax E_s \\lesssim \\int_0\^T P_{\\max}\\,dt = TP_{\\max} Es≲∫0TPmaxdt=TPmax 若噪声谱密度固定,则能量信噪比 SNR=EsN0∝TPmax \\mathrm{SNR}=\\frac{E_s}{N_0}\\propto TP_{\\max} SNR=N0Es∝TPmax 代入 TOA CRLB(忽略常数): Var(τ\^)≳1β2SNR∝1β2 T Pmax \\mathrm{Var}(\\hat\\tau)\\gtrsim \\frac{1}{\\beta\^2\\mathrm{SNR}} \\propto \\frac{1}{\\beta\^2\\,T\\,P_{\\max}} Var(τ\^)≳β2SNR1∝β2TPmax1 这就把"测距前导更长更准"的经验规律与 (13) 的理论下界连成了同一条链。与此同时也能解释 TfT_fTf 的双重约束:增大 TfT_fTf 可提高单脉冲能量上限(在平均功率受限下),但会推高峰值功率需求并可能触碰硬件/法规的峰值限制;减小 TfT_fTf 又可能使多径尾巴跨帧叠加导致帧间干扰。