自动驾驶控制算法——模型预测控制（MPC）

目前主流的轨迹跟踪方法有两类：基于几何模型的跟踪方法和基于动力学模型的跟踪方法。

基于几何模型的跟踪方法：

Pure Pursuit
Stanley

基于动力学模型的跟踪方法:

0.文章目录

[1. 最优化控制与MPC](#1. 最优化控制与MPC)
- [1.1 最优控制的基本概念](#1.1 最优控制的基本概念)
- [1.2 MPC的基本概念](#1.2 MPC的基本概念)
- [1.3 MPC推导](#1.3 MPC推导)
[2. MPC 案例](#2. MPC 案例)
[3. 最优化控制、PID、LQR、MPC](#3. 最优化控制、PID、LQR、MPC)
- [3.1 最优化控制 vs MPC](#3.1 最优化控制 vs MPC)
- [3.2 PID vs MPC](#3.2 PID vs MPC)
- [3.3 LQR vs MPC](#3.3 LQR vs MPC)
[4. Apollo中MPC算法](#4. Apollo中MPC算法)
[5. MPC算法使用过程中遇到的问题](#5. MPC算法使用过程中遇到的问题)
- [1. 如何设置约束来加快求解？](#1. 如何设置约束来加快求解？)
- [2. MPC可行域的设置，预测/控制时域的设置](#2. MPC可行域的设置，预测/控制时域的设置)
- [3. 调整迭代次数及对结果的容忍度](#3. 调整迭代次数及对结果的容忍度)
- [4. MPC控制器参数调节难！！终端代价](#4. MPC控制器参数调节难！！终端代价)
- [5. 如何考虑控制器稳定性问题？](#5. 如何考虑控制器稳定性问题？)
- [6. 加快MPC求解速度的方法？](#6. 加快MPC求解速度的方法？)

模型预测控制（Model Predictive Control, MPC） ，是一种广泛应用于工业领域的高级控制策略。MPC的基本思想是利用当前时刻系统的状态及约束，对未来一段时间内系统的状态和输入进行预测，从而求解出一组最优的控制序列，然后取出第一组控制序列用于下一时刻系统控制。在下一时刻，重复上述步骤。

首先，明确三个基本概念：

模型
- 机理模型；
- 基于数据的模型（例如用机器学习或神经网络训练的一个model）；
预测
- 模型就是用来预测系统未来状态的，预测的目的是为了更好的决策；
控制
- 根据预测，作出决策，得到最优的控制序列，用于驱动系统前进；

1. 最优化控制与MPC

1.1 最优控制的基本概念

最优控制（optimal control）指的是在一定的约束情况下达到最优状态的系统表现。

这里有2个概念需要注意：

约束：一般是物理限制，如最大方向盘转角，汽车最大加速度；
最优：这是一个相对概念，并不是绝对的，不同的评价标准最优的结果也不一样，所以需要具体问题具体分析；

所以到底什么是最优？我们通常通过代价函数（目标函数）来衡量，同时代价函数还受约束的限制。

对于单输入单输出系统（SISO）而言，衡量系统性能优劣可以用误差的积累值 ∫ 0 ∞ e 2 d t \int_{0}^{\infty } e^{2} dt ∫0∞e2dt和输入的积累值 ∫ 0 ∞ u 2 d t \int_{0}^{\infty } u^{2} dt ∫0∞u2dt来衡量。由此，我们可以定义代价函数：
J = ∫ 0 ∞ e 2 d t + ∫ 0 ∞ u 2 d t (1) J = \int_{0}^{\infty } e^{2} dt + \int_{0}^{\infty } u^{2} dt \tag{1} J=∫0∞e2dt+∫0∞u2dt(1)

这是一个同时考虑系统误差（状态）和系统能耗的代价函数，为了更好的权衡误差的能耗的比重，可以在代价函数中加入调节参数：
J = ∫ 0 ∞ q e 2 d t + ∫ 0 ∞ r u 2 d t (2) J = \int_{0}^{\infty }q e^{2} dt + \int_{0}^{\infty } ru^{2} dt \tag{2} J=∫0∞qe2dt+∫0∞ru2dt(2)

我们可以通过调节 r r r和 q q q的比例，来使代价函数是更看重误差还是能耗表现。这里也可以看出，所谓最优，其实是一个相对的概念。

对于多输入多输出系统（MIMO），其状态空间可以描述为：
x ˙ = A x + B u y = C x (3) \begin{aligned} \dot{x} = & Ax+Bu\\ y=&Cx \end{aligned}\tag{3} x˙=y=Ax+BuCx(3)

代价函数：
J = ∫ 0 ∞ e T Q e d t + ∫ 0 ∞ u T R u d t (4) J = \int_{0}^{\infty }e^{T} Q edt + \int_{0}^{\infty } u^{T} R u dt\tag{4} J=∫0∞eTQedt+∫0∞uTRudt(4)

其中：

e e e是系统误差，可以通过状态空间方程转换得到， Q Q Q是系统状态权重矩阵；
u u u是系统误差， R R R是系统误差权重矩阵

多输入系统其状态空间方程，通常可以转换成误差的方程。因此我们可以通过调节 Q Q Q矩阵和 R R R中的权重系数，来使代价函数在优化的过程中更看重那一项误差或输入。

1.2 MPC的基本概念

最优控制强调的是"最优"，一般最优控制需要在整个时间域上进行求优化。所以最优控制中的代价函数是从0到正无穷时刻的积分，这是一种很贪婪的行为，需要消耗大量算力；同时，系统如果是一个时变系统，或者面临扰动的话，前一时刻得到的最优并不一定是下一时刻的最优值。

因而我们引入模型预测控制的概念，对于一个离散化系统，MPC通过模型来预测系统在未来某一段时间内的表现来进行优化控制。这一有限的时间段被称为预测区间（Predictive Horizon）： N p N_{p} Np，而这一段时间内控制估计的部分称为控制区间（Control Horizon）： N c N_{c} Nc。通常 N c = N p N_{c} = N_{p} Nc=Np，在某些情况下为了节省计算资源，会选择 N c < N p N_{c} < N_{p} Nc<Np，当时间超过控制区间后，控制量将保持为常数。后面的推导，我们取 N c = N p N_{c} = N_{p} Nc=Np。

如下图所示，在k时刻，我们可以测量或估计出系统的当前状态 Y k Y_{k} Yk，再通过计算得到一组最优控制序列的： u k , u k + 1 , u k + 2 , ⋯ , u k + N c − 1 u_{k} ,u_{k+1} ,u_{k+2} ,\cdots ,u_{k+N_{c}-1 } uk,uk+1,uk+2,⋯,uk+Nc−1，同时根据系统模型预测系统在这样的最优控制序列下，状态未来的变化序列： Y k , Y k + 1 , Y k + 2 , ⋯ , Y k + N p Y_{k} ,Y_{k+1} ,Y_{k+2} ,\cdots ,Y_{k+N_{p}} Yk,Yk+1,Yk+2,⋯,Yk+Np。在得到最优输入之后，我们只施加当前时刻的输入 u k u_{k} uk。

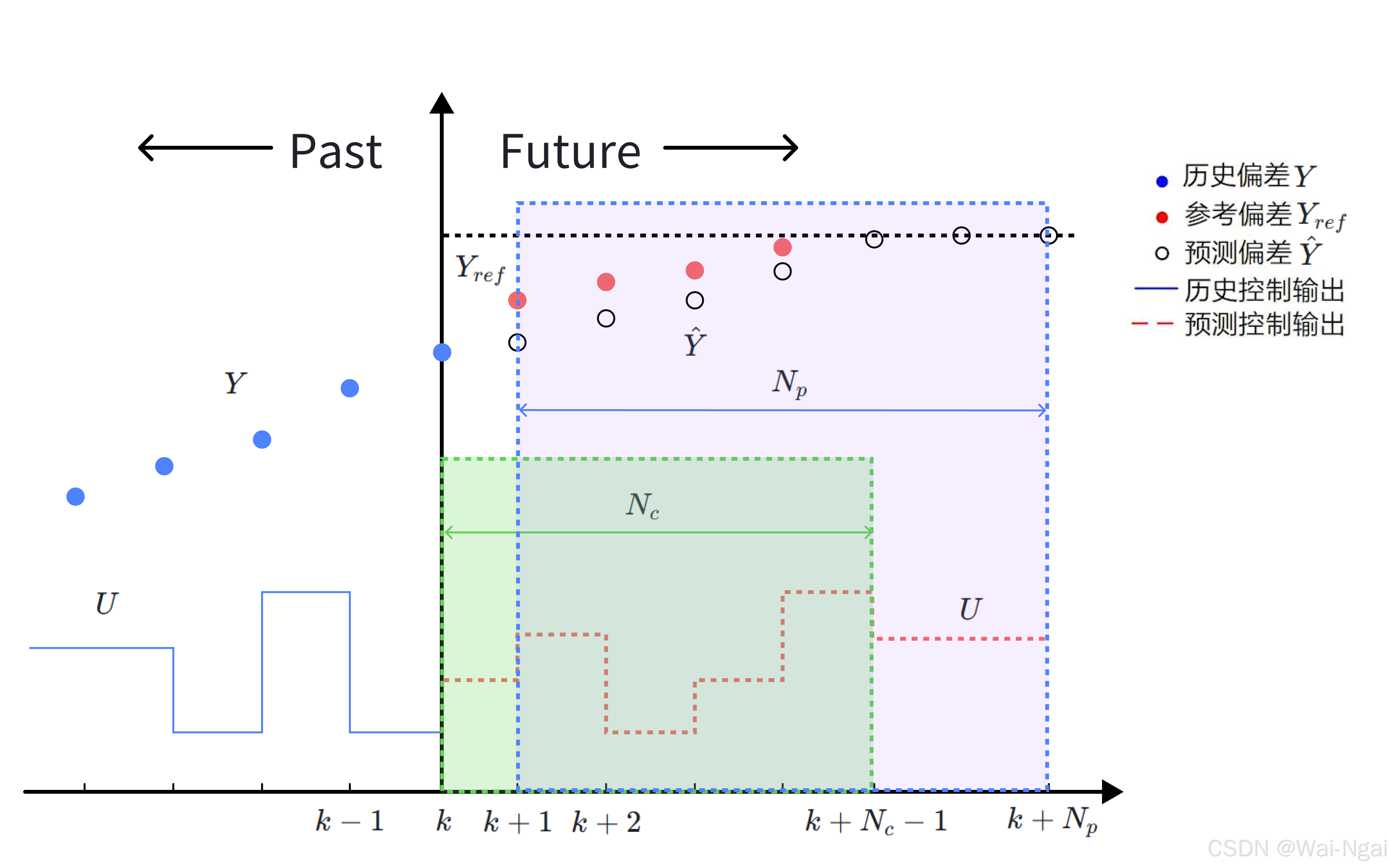
综上，MPC主要分为三步，在k时刻：

状态估计 ：估计/测量系统当前状态；
a. 如果系统的状态无法观测，就需要进行估计，这就涉及估计器的设计。
优化求解 ：基于当前状态和系统模型，在未来的预测时域 N p N_{p} Np内，求解一组最优的控制序列 u k , u k + 1 , u k + 2 , ⋯ , u k + N c − 1 u_{k} ,u_{k+1} ,u_{k+2} ,\cdots ,u_{k+N_{c} -1} uk,uk+1,uk+2,⋯,uk+Nc−1，使得某个代价函数最小；
滚动实施 ：只取 u k u_{k} uk，用于系统控制；
a. 因为预测的模型很难描述现实的系统，存在不确定性，当前时刻测量的系统状态也可能存在误差，另外现实的系统中可能存在扰动，所以在实际控制中只选取预测区间内最优控制序列的第一组控制 u k u_{k} uk施加到系统中。
b. 这里有个问题：**既然最后只选取一组控制，为什么优化的时候不直接只优化这一组控制？**这是因为MPC的"滚动优化"特性决定了，我们当前计算出的"第一组"控制作用，其最优性是严重依赖于对未来状态的预测的。而为了做出准确的预测，我们必须同时考虑未来一段时域内所有的控制序列。因此，优化整个未来控制序列，正是为了计算出当前时刻那个真正"最优"的、具有远见的第一个控制作用。这是MPC强大性能的根本来源。

在下一时刻重复以上三步，在下一步进行预测时使用的就是下一步的状态值，我们将这样的方案称为滚动优化控制（Receding Horizon Control）。

可以看到，每一步（周期）都需要求解一个最优化问题，所以MPC对于控制器的算力要求很高，同时求解最优化问题的时候，还可以考虑约束。

对于MPC问题，有很多种方法来进行最优化，很多MPC问题（线性MPC）最后都可以形成一个**二次规划(Quadratic Programming)**问题，所以MPC表面是控制，实际上是一个优化方法，MPC的每一个周期都在求解一个带约束的优化问题。

二次规划一般形式
m i n i m i z e 1 2 x T H x + f T x s u b s c i r b e t o l ≤ A x ≤ u (5) minimize\quad\frac{1}{2}x^{T}Hx+f^{T}x\\ subscirbe\ to\quad l\leq Ax\leq u\\ \tag{5} minimize21xTHx+fTxsubscirbe tol≤Ax≤u(5)

其中，

第一个式子是代价函数：

x ∈ R n x \in \R^n x∈Rn是待优化的参数；
H ∈ S + n H\in S^n_+ H∈S+n(Hessian矩阵) 是一个对称半正定矩阵，决定了目标函数中二次项的形状，它的正定性保证了问题的凸性；
f ∈ R n f\in R^n f∈Rn (梯度向量) 是线性项系数向量，它决定了优化方向的"梯度"或"趋势"，它直接影响最优解的位置；

第二个式子是约束函数， l l l(lower bound)和 u u u (upper bound)分别代表约束的上下限，都是m维向量，表示m个约束函数，约束矩阵 A ∈ R m × n A\in R^{m\times n} A∈Rm×n

需要说明的是，包括等式约束，不等式约束，变量 x x x的取值范围： { A x ≤ b A e q x = b e q l b ≤ x ≤ u b \begin{cases} Ax & \le b \\ A_{eq} x &= b_{eq} \\ lb &\le x \le ub \end{cases} ⎩ ⎨ ⎧AxAeqxlb≤b=beq≤x≤ub都可以转换成统一表达形式： l ≤ A x ≤ u l\leq Ax\leq u l≤Ax≤u。

前面部分 1 2 x T H x + f T x \frac{1}{2}x^{T}Hx+f^{T}x 21xTHx+fTx是二次型的 ，后面部分 f T x f^{T}x fTx是线性的。如果没有前面部分，就变成一个线性规划了。

处理二次规划问题，现在已经比较成熟，有很多现成的工具或库。所以现在要做的就是将MPC问题转换成QP的一般形式，这样就可以利用QP的求解工具。

下面是一些MPC的求解器，可以用于线性MPC和非线性MPC。

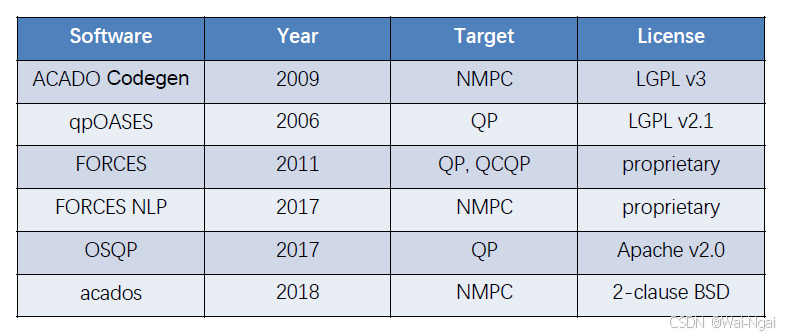
1.3 MPC推导

下面的推导针对线性MPC，并且没有考虑约束。

对于离散线性时不变系统 的状态空间方程：
x ( k + 1 ) = A x ( k ) + B u ( k ) (6) x_{\left (k+1\right )} = Ax_{\left (k\right )} + Bu_{\left (k\right )} \tag{6} x(k+1)=Ax(k)+Bu(k)(6)

其中，

x ( k ) x_{\left (k\right )} x(k)为状态向量， x ( k ) = [ x 1 x 2 ⋮ x n ] n × 1 x_{\left (k\right )}= \begin{bmatrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{bmatrix}{{\color{Red} n \times 1} } x(k)= x1x2⋮xn n×1， u ( k ) u{\left (k\right )} u(k)为控制向量， u ( k ) = [ u 1 u 2 ⋮ u p ] p × 1 u_{\left (k\right )}= \begin{bmatrix} u_{1} \\ u_{2} \\ \vdots \\ u_{p} \\ \end{bmatrix}_{{\color{Red} p \times 1} } u(k)= u1u2⋮up p×1；
A A A为 n × n {\color{Red} n \times n} n×n状态矩阵， B B B为 n × p {\color{Red} n \times p} n×p输入矩阵；

在模型预测控制中，取预测区间为 N p N_{p} Np，则记k时刻的系统初始状态向量为 x ( k ∣ k ) x_{\left ( k\mid k \right ) } x(k∣k)，初始控制向量为 u ( k ∣ k ) u_{\left ( k\mid k \right ) } u(k∣k)，k时刻预测k+1时刻的系统状态向量为 x ( k + 1 ∣ k ) x_{\left ( k+1\mid k \right ) } x(k+1∣k)，k时刻计算k+1时刻的系统控制向量为 u ( k + 1 ∣ k ) u_{\left ( k+1\mid k \right ) } u(k+1∣k)，后面的记号依次类推。

从调节问题 （控制目标为0）入手，定义二次型代价函数 ：
J = 1 2 x ( k + N p ∣ k ) T F x ( k + N p ∣ k ) + 1 2 ∑ i = 0 N p − 1 ( x ( k + i ∣ k ) T Q x ( k + i ∣ k ) + u ( k + i ∣ k ) T R u ( k + i ∣ k ) ) (7) J = \frac{1}{2} { x_{\left (k+ N_{p} \mid k \right )}^{T} } F x_{\left (k+ N_{p} \mid k \right )} + \frac{1}{2}\sum_{i=0}^{N_{p} -1} \left ( { x_{\left (k+ i \mid k \right )}^{T} } Q x_{\left (k+ i \mid k \right )}+ { u_{\left (k+ i \mid k \right )}^{T} } R u_{\left (k+ i \mid k \right )} \right ) \tag{7} J=21x(k+Np∣k)TFx(k+Np∣k)+21i=0∑Np−1(x(k+i∣k)TQx(k+i∣k)+u(k+i∣k)TRu(k+i∣k))(7)

其中：

第一项 1 2 x ( k + N p ∣ k ) T F x ( k + N p ∣ k ) \frac{1}{2} { x_{\left (k+ N_{p} \mid k \right )}^{T} } F x_{\left (k+ N_{p} \mid k \right )} 21x(k+Np∣k)TFx(k+Np∣k)，为系统终端代价；
第二项 1 2 ∑ i = 0 N p − 1 ( x ( k + i ∣ k ) T Q x ( k + i ∣ k ) + u ( k + i ∣ k ) T R u ( k + i ∣ k ) ) \frac{1}{2}\sum_{i=0}^{N_{p} -1} \left ( { x_{\left (k+ i \mid k \right )}^{T} } Q x_{\left (k+ i \mid k \right )}+ { u_{\left (k+ i \mid k \right )}^{T} } R u_{\left (k+ i \mid k \right )} \right ) 21∑i=0Np−1(x(k+i∣k)TQx(k+i∣k)+u(k+i∣k)TRu(k+i∣k))，为系统运行代价；
F = [ f 1 ... 0 0 ⋱ 0 0 ... f n ] , f 1 , f 2 , ... , f n ≥ 0 F = \begin{bmatrix} f_{1} & \dots & 0\\ 0 & \ddots & 0\\ 0 & \dots & f_{n} \end{bmatrix}, \begin{matrix} &f_{1},f_{2},\dots,f_{n}\ge 0 \end{matrix} F= f100...⋱...00fn ,f1,f2,...,fn≥0，为终端代价权重矩阵；
Q = [ q 1 ... 0 0 ⋱ 0 0 ... q n ] , q 1 , q 2 , ... , q n ≥ 0 Q = \begin{bmatrix} q_{1} & \dots & 0\\ 0 & \ddots & 0\\ 0 & \dots & q_{n} \end{bmatrix}, \begin{matrix} &q_{1},q_{2},\dots,q_{n}\ge 0 \end{matrix} Q= q100...⋱...00qn ,q1,q2,...,qn≥0，为状态权重矩阵；
R = [ r 1 ... 0 0 ⋱ 0 0 ... r n ] , r 1 , r 2 , ... , r n > 0 R = \begin{bmatrix} r_{1} & \dots & 0\\ 0 & \ddots & 0\\ 0 & \dots & r_{n} \end{bmatrix}, \begin{matrix} &r_{1},r_{2},\dots,r_{n}> 0 \end{matrix} R= r100...⋱...00rn ,r1,r2,...,rn>0，为控制权重矩阵；

对比MPC的代价函数和二次规划的一般形式，可以发现二次规划是关于待优化参数的函数，只有一个优化变量，而上述MPC的代价函数，包含控制和状态2个优化变量，因此需要想办法消除状态变量，留下控制变量（因为这是我们需要优化的），这样转换成二次规划的形式。

接下来，我们对整个预测区间 N p N_{p} Np内的系统状态变化进行递推。

k时刻的系统状态：
x ( k ∣ k ) = x ( k ) (8) {\color{Green} x_{\left ( k\mid k \right ) }} = x_{\left (k\right )} \tag{8} x(k∣k)=x(k)(8)
k时刻预测k+1时刻的系统状态：
x ( k + 1 ∣ k ) = A x ( k ∣ k ) + B u ( k ∣ k ) = A x ( k ) + B u ( k ∣ k ) (9) \begin{aligned} {\color{Purple} x_{\left (k+1\mid k \right )}} & = A{\color{Green} x_{\left (k \mid k \right )}} + Bu_{\left (k\mid k \right )}\\ & = A{ x_{\left ( k \right )}} + Bu_{\left (k\mid k \right )} \end{aligned}\tag{9} x(k+1∣k)=Ax(k∣k)+Bu(k∣k)=Ax(k)+Bu(k∣k)(9)
k时刻预测k+2时刻的系统状态：
x ( k + 2 ∣ k ) = A x ( k + 1 ∣ k ) + B u ( k + 1 ∣ k ) = A [ A x ( k ) + B u ( k ∣ k ) ] + B u ( k + 1 ∣ k ) = A 2 x ( k ) + A B u ( k ∣ k ) + B u ( k + 1 ∣ k ) (10) \begin{aligned} {\color{Red} x_{\left (k+2\mid k \right )}} & = Ax_{\left (k+1 \mid k \right )} + Bu_{\left (k+1\mid k \right )} \\ & = A\left [ A{ x_{\left ( k \right )}} + Bu_{\left (k\mid k \right )}\right ] + Bu_{\left (k+1\mid k \right )} \\ & =A^{2} { x_{\left ( k \right )}} + ABu_{\left (k\mid k \right )}+ Bu_{\left (k+1\mid k \right )} \end{aligned} \tag{10} x(k+2∣k)=Ax(k+1∣k)+Bu(k+1∣k)=A[Ax(k)+Bu(k∣k)]+Bu(k+1∣k)=A2x(k)+ABu(k∣k)+Bu(k+1∣k)(10)
k时刻预测k+3时刻的系统状态：
x ( k + 3 ∣ k ) = A x ( k + 2 ∣ k ) + B u ( k + 2 ∣ k ) = A [ A 2 x ( k ) + A B u ( k ∣ k ) + B u ( k + 1 ∣ k ) ] + B u ( k + 2 ∣ k ) = A 3 x ( k ) + A 2 B u ( k ∣ k ) + A B u ( k + 1 ∣ k ) + B u ( k + 2 ∣ k ) (11) \begin{aligned} { x_{\left (k+3\mid k \right )}} & = A {\color{Red} x_{\left (k+2 \mid k \right )}} + Bu_{\left (k+2\mid k \right )} \\ & = A\left [ A^{2} { x_{\left ( k \right )}} + ABu_{\left (k\mid k \right )}+ Bu_{\left (k+1\mid k \right )} \right ] + Bu_{\left (k+2\mid k \right )} \\ & = A^{3} { x_{\left ( k \right )}} + A^{2}Bu_{\left (k\mid k \right )}+ ABu_{\left (k+1\mid k \right )} + Bu_{\left (k+2\mid k \right )} \end{aligned} \tag{11} x(k+3∣k)=Ax(k+2∣k)+Bu(k+2∣k)=A[A2x(k)+ABu(k∣k)+Bu(k+1∣k)]+Bu(k+2∣k)=A3x(k)+A2Bu(k∣k)+ABu(k+1∣k)+Bu(k+2∣k)(11)
依次，递推到k时刻预测k+Np时刻的系统状态：
x ( k + N p ∣ k ) = A x ( k + N p − 1 ∣ k ) + B u ( k + N p − 1 ∣ k ) = A [ A N p − 1 x ( k ) + A N p − 2 B u ( k ∣ k ) + ⋯ + B u ( k + N p − 2 ∣ k ) ] + B u ( k + N p − 1 ∣ k ) = A N p x ( k ) + A N p − 1 B u ( k ∣ k ) + ⋯ + A B u ( k + N p − 2 ∣ k ) + B u ( k + N p − 1 ∣ k ) (12) \begin{aligned} { x_{\left (k+ N_{p} \mid k \right )}} & = A {\color{blue} x_{\left (k+ N_{p} -1 \mid k \right )}} + Bu_{\left (k+N_{p} -1\mid k \right )} \\ & = A\left [ A^{N_{p}-1} { x_{\left ( k \right )}} + A^{N_{p}-2}Bu_{\left (k\mid k \right )} + \dots +Bu_{\left (k+N_{p} -2\mid k \right )} \right ] + Bu_{\left (k+N_{p} -1\mid k \right )} \\ & = A^{N_{p}} { x_{\left ( k \right )}} + A^{N_{p}-1}Bu_{\left (k\mid k \right )}+ \dots + A Bu_{\left (k+N_{p} -2 \mid k \right )} + Bu_{\left (k+N_{p} -1 \mid k \right )} \end{aligned} \tag{12} x(k+Np∣k)=Ax(k+Np−1∣k)+Bu(k+Np−1∣k)=A[ANp−1x(k)+ANp−2Bu(k∣k)+⋯+Bu(k+Np−2∣k)]+Bu(k+Np−1∣k)=ANpx(k)+ANp−1Bu(k∣k)+⋯+ABu(k+Np−2∣k)+Bu(k+Np−1∣k)(12)

将上述k时刻预测区间 N p N_{p} Np内的系统状态变化的递推写成矩阵的形式：

状态向量权重，控制向量权重分别为：

Q = [ 100 0 0 1 ] Q = \begin{bmatrix} 100 & 0\\ 0 & 1 \end{bmatrix} Q=[100001]， F = [ 100 0 0 1 ] F = \begin{bmatrix} 100 & 0\\ 0 & 1 \end{bmatrix} F=[100001]， R = [ 1 0 0 0.1 ] R = \begin{bmatrix} 1 & 0\\ 0 & 0.1 \end{bmatrix} R=[1000.1]

设预测区间 N p = 5 N_{p} = 5 Np=5，则 n = 2 n = 2 n=2， p = 2 p = 2 p=2，则预测区间内的状态变量向量和控制变量向量：

X ( k ) = [ x 1 ( k ∣ k ) x 2 ( k ∣ k ) x 1 ( k + 1 ∣ k ) x 2 ( k + 1 ∣ k ) x 1 ( k + 2 ∣ k ) x 2 ( k + 2 ∣ k ) x 1 ( k + 3 ∣ k ) x 2 ( k + 3 ∣ k ) x 1 ( k + 4 ∣ k ) x 2 ( k + 4 ∣ k ) x 1 ( k + 5 ∣ k ) x 2 ( k + 5 ∣ k ) ] 12 × 1 {\color{Green} X_{\left ( k \right ) }} = \begin{bmatrix} x_{1\left ( k\mid k \right ) }\\ x_{2\left ( k\mid k \right ) }\\ x_{1\left ( k+1\mid k \right ) }\\ x_{2\left ( k+1\mid k \right ) }\\ x_{1\left ( k+2\mid k \right ) }\\ x_{2\left ( k+2\mid k \right ) }\\ x_{1\left ( k+3\mid k \right ) }\\ x_{2\left ( k+3\mid k \right ) }\\ x_{1\left ( k+4\mid k \right ) }\\ x_{2\left ( k+4\mid k \right ) }\\ x_{1\left ( k+5\mid k \right ) }\\ x_{2\left ( k+5\mid k \right ) } \end{bmatrix} {{\color{Red} 12 \times 1} } X(k)= x1(k∣k)x2(k∣k)x1(k+1∣k)x2(k+1∣k)x1(k+2∣k)x2(k+2∣k)x1(k+3∣k)x2(k+3∣k)x1(k+4∣k)x2(k+4∣k)x1(k+5∣k)x2(k+5∣k) 12×1， U ( k ) = [ u 1 ( k ∣ k ) u 2 ( k ∣ k ) u 1 ( k + 1 ∣ k ) u 2 ( k + 1 ∣ k ) u 1 ( k + 2 ∣ k ) u 2 ( k + 2 ∣ k ) u 1 ( k + 3 ∣ k ) u 2 ( k + 3 ∣ k ) u 1 ( k + 4 ∣ k ) u 2 ( k + 4 ∣ k ) ] 10 × 1 {\color{blue} U{\left ( k \right ) }} = \begin{bmatrix} u_{1\left ( k\mid k \right ) }\\ u_{2\left ( k\mid k \right ) }\\ u_{1\left ( k+1\mid k \right ) }\\ u_{2\left ( k+1\mid k \right ) }\\ u_{1\left ( k+2\mid k \right ) }\\ u_{2\left ( k+2\mid k \right ) }\\ u_{1\left ( k+3\mid k \right ) }\\ u_{2\left ( k+3\mid k \right ) }\\ u_{1\left ( k+4\mid k \right ) }\\ u_{2\left ( k+4\mid k \right ) } \end{bmatrix} _{{\color{Red} 10 \times 1} } U(k)= u1(k∣k)u2(k∣k)u1(k+1∣k)u2(k+1∣k)u1(k+2∣k)u2(k+2∣k)u1(k+3∣k)u2(k+3∣k)u1(k+4∣k)u2(k+4∣k) 10×1，

矩阵 M M M和 C C C：

M = [ 1 0 0 1 1 0.1 − 1 2 0.9 0.3 − 3 3.9 0.6 0.69 − 6.9 7.5 − 0.09 1.44 − 14.4 14.31 − 1.53 2.871 − 28.71 27.18 ] 12 × 2 , C = [ 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.2 1 0 0 0 0 0 0 0 0 0.5 2 0 0 0 0 0 0 0 0 0.25 1.2 0.2 1 0 0 0 0 0 0 0.8 3 0.5 2 0 0 0 0 0 0 0.465 1.98 0.25 1.2 0.2 1 0 0 0 0 2.37 8.1 0.8 3 0.5 2 0 0 0 0 1.914 6.777 0.465 1.98 0.25 1.2 0.2 1 0 0 14.567 47.088 2.37 8.1 0.8 3 0.5 2 0 0 20.804 67.197 1.914 6.777 0.465 1.98 0.25 1.2 0.2 1 180.891 576.240 14.567 47.088 2.37 8.1 0.8 3 0.5 2 ] 12 × 10 M = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 0.1 \\ -1 & 2 \\ 0.9 & 0.3 \\ -3 & 3.9 \\ 0.6 & 0.69 \\ -6.9 & 7.5 \\ -0.09 & 1.44 \\ -14.4 & 14.31 \\ -1.53 & 2.871 \\ -28.71 & 27.18 \end{bmatrix}_{{\color{Red} 12 \times 2} } , \quad C = \begin{bmatrix} 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0.2 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0.5 & 2 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0.25 & 1.2 & 0.2 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0.8 & 3 & 0.5 & 2 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0.465 & 1.98 & 0.25 & 1.2 & 0.2 & 1 & 0 & 0 & 0 & 0 \\ 2.37 & 8.1 & 0.8 & 3 & 0.5 & 2 & 0 & 0 & 0 & 0 \\ 1.914 & 6.777 & 0.465 & 1.98 & 0.25 & 1.2 & 0.2 & 1 & 0 & 0 \\ 14.567 & 47.088 & 2.37 & 8.1 & 0.8 & 3 & 0.5 & 2 & 0 & 0 \\ 20.804 & 67.197 & 1.914 & 6.777 & 0.465 & 1.98 & 0.25 & 1.2 & 0.2 & 1 \\ 180.891 & 576.240 & 14.567 & 47.088 & 2.37 & 8.1 & 0.8 & 3 & 0.5 & 2 \end{bmatrix} _{{\color{Red} 12 \times 10} } M= 101−10.9−30.6−6.9−0.09−14.4−1.53−28.71010.120.33.90.697.51.4414.312.87127.18 12×2,C= 000.20.50.250.80.4652.371.91414.56720.804180.89100121.231.988.16.77747.08867.197576.24000000.20.50.250.80.4652.371.91414.5670000121.231.988.16.77747.0880000000.20.50.250.80.4652.37000000121.231.988.1000000000.20.50.250.800000000121.2300000000000.20.5000000000012 12×10

矩阵 Q ˉ \bar{Q} Qˉ和 R ˉ \bar{R} Rˉ：
Q ˉ = [ 100 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 100 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 100 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 100 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 100 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 100 0 0 0 0 0 0 0 0 0 0 0 0 1 ] 12 × 12 , R ˉ = [ 1 0 0 0 0 0 0 0 0 0 0 0.1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0.1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0.1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0.1 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0.1 ] 10 × 10 \bar{Q} = \begin{bmatrix} 100 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 100 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 100 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 100 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 100 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 100 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{bmatrix} _{{\color{Red} 12 \times 12} } , \quad \bar{R} = \begin{bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0.1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0.1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0.1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0.1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0.1 \end{bmatrix} _{{\color{Red} 10 \times 10} } Qˉ= 100000000000000100000000000010000000000000010000000000001000000000000001000000000000100000000000000100000000000010000000000000010000000000001000000000000001 12×12,Rˉ= 100000000000.10000000000100000000000.10000000000100000000000.10000000000100000000000.10000000000100000000000.1 10×10

矩阵 E E E和 H H H只给最终数值结果（由编程得到，手算太繁琐）：

E ≈ [ − 8551.234 − 27301.141 − 723.414 − 2387.937 − 144.408 − 543.291 − 70.218 − 307.53 − 44.955 − 210.42 11436.875 36857.459 1077.515 3769.3 262.916 1088.346 129.474 598.68 71.01 341.46 ] 2 × 10 E \approx \begin{bmatrix} -8551.234 & -27301.141 & -723.414 & -2387.937 & -144.408 & -543.291 & -70.218 & -307.53 & -44.955 & -210.42 \\ 11436.875 & 36857.459 & 1077.515 & 3769.3 & 262.916 & 1088.346 & 129.474 & 598.68 & 71.01 & 341.46 \end{bmatrix}_{{\color{Red} 2 \times 10} } E≈[−8551.23411436.875−27301.14136857.459−723.4141077.515−2387.9373769.3−144.408262.916−543.2911088.346−70.218129.474−307.53598.68−44.95571.01−210.42341.46]2×10

H ≈ [ 794781.09 2552328.5 83978.17 277024.66 8448.45 27871.36 851.16 2805.73 86.04 283.54 2552328.5 8198048.2 269773.66 889788.1 27142.97 89525.62 2734.18 9013.84 276.36 910.94 83978.17 269773.66 8887.19 29306.94 897.19 2957.75 90.36 297.89 9.13 30.09 277024.66 889788.1 29306.94 96641.23 2958.97 9755.31 297.95 982.14 30.10 99.19 8448.45 27142.97 897.19 2958.97 905.21 2984.75 91.18 300.59 9.21 30.35 27871.36 89525.62 2957.75 9755.31 2984.75 9841.04 300.61 990.94 30.36 100.08 851.16 2734.18 90.36 297.95 91.18 300.61 91.20 300.66 9.22 30.38 2805.73 9013.84 297.89 982.14 300.59 990.94 300.66 991.05 30.38 100.14 86.04 276.36 9.13 30.10 9.21 30.36 9.22 30.38 9.22 30.39 283.54 910.94 30.09 99.19 30.35 100.08 30.38 100.14 30.39 100.15 ] 10 × 10 H \approx \begin{bmatrix} 794781.09 & 2552328.5 & 83978.17 & 277024.66 & 8448.45 & 27871.36 & 851.16 & 2805.73 & 86.04 & 283.54 \\ 2552328.5 & 8198048.2 & 269773.66 & 889788.1 & 27142.97 & 89525.62 & 2734.18 & 9013.84 & 276.36 & 910.94 \\ 83978.17 & 269773.66 & 8887.19 & 29306.94 & 897.19 & 2957.75 & 90.36 & 297.89 & 9.13 & 30.09 \\ 277024.66 & 889788.1 & 29306.94 & 96641.23 & 2958.97 & 9755.31 & 297.95 & 982.14 & 30.10 & 99.19 \\ 8448.45 & 27142.97 & 897.19 & 2958.97 & 905.21 & 2984.75 & 91.18 & 300.59 & 9.21 & 30.35 \\ 27871.36 & 89525.62 & 2957.75 & 9755.31 & 2984.75 & 9841.04 & 300.61 & 990.94 & 30.36 & 100.08 \\ 851.16 & 2734.18 & 90.36 & 297.95 & 91.18 & 300.61 & 91.20 & 300.66 & 9.22 & 30.38 \\ 2805.73 & 9013.84 & 297.89 & 982.14 & 300.59 & 990.94 & 300.66 & 991.05 & 30.38 & 100.14 \\ 86.04 & 276.36 & 9.13 & 30.10 & 9.21 & 30.36 & 9.22 & 30.38 & 9.22 & 30.39 \\ 283.54 & 910.94 & 30.09 & 99.19 & 30.35 & 100.08 & 30.38 & 100.14 & 30.39 & 100.15 \end{bmatrix}_{{\color{Red} 10 \times 10} } H≈ 794781.092552328.583978.17277024.668448.4527871.36851.162805.7386.04283.542552328.58198048.2269773.66889788.127142.9789525.622734.189013.84276.36910.9483978.17269773.668887.1929306.94897.192957.7590.36297.899.1330.09277024.66889788.129306.9496641.232958.979755.31297.95982.1430.1099.198448.4527142.97897.192958.97905.212984.7591.18300.599.2130.3527871.3689525.622957.759755.312984.759841.04300.61990.9430.36100.08851.162734.1890.36297.9591.18300.6191.20300.669.2230.382805.739013.84297.89982.14300.59990.94300.66991.0530.38100.1486.04276.369.1330.109.2130.369.2230.389.2230.39283.54910.9430.0999.1930.35100.0830.38100.1430.39100.15 10×10

下面使用MATLAB进行计算，MATLAB中可以调用函数x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0)进行二次型求解。

MPC_Test.m

matlab 复制代码

% 清屏
clear;
close all;
clc;

%%% 状态空间方程 x(k+1) = Ax(k) + Bu(k)
A = [1 0.1;
    -1 2];                                % 定义状态矩阵 A, n*n 矩阵
B = [0.2 1;
     0.5 2];                              % 定义输入矩阵 B, n*p 矩阵
n = size(A, 1);
p = size(B, 2);

Q = [100 0;
     0   1];                              % 定义Q矩阵，n*n 矩阵，状态向量权重
F = [100 0;
     0   1];                              % 定义F矩阵，n*n 矩阵，终端误差权重
R = [1  0;
     0  0.1];                             % 定义R矩阵，p*p 矩阵，控制向量权重
N = 5;                                    % 定义预测区间N

k_steps = 100;                            % 定义计算总长度step数量k

X_K = zeros(n, k_steps);                  % 定义矩阵 X_K， n*k 矩 阵，用于保存所有状态
U_K = zeros(p, k_steps);                  % 定义输入矩阵 U_K， p*k 矩阵，用于保存所有控制

X_K(:,1) = [20; -20];                     % 初始状态变量值， n*1 向量


% 计算E,H矩阵
[E,H] = MPC_Matrices(A, B, Q, R, F, N);

% 计算每一步的状态变量的值
for k = 1 : k_steps
    U_K(:,k) = Prediction(X_K(:,k), E, H, N, p);    % 求得U_K(:,k) 
    X_K(:,k+1) = A * X_K(:,k) + B * U_K(:,k);       % 计算第k+1步时状态变量的值
end


% 绘制状态变量和输入的变化
subplot(2, 1, 1);
hold;
for i = 1 : size(X_K,1)
    plot(X_K(i,:));
end
legend("x1","x2")
hold off;
subplot(2, 1, 2);
hold;
for i = 1 : size(U_K,1)
    plot(U_K(i,:));
end
legend("u1","u2")

Prediction.m

matlab 复制代码

function u_k= Prediction(x_k, E, H, N, p)

U_k = zeros(N * p, 1);        % NP x 1

% H 二次目标项，对称实矩阵
% f 线性目标项，实数向量
U_k = quadprog(H, E * x_k);

u_k = U_k(1 : p, 1);          % 取第一个结果

MPC_Matrices.m

matlab 复制代码

function [E,H] = MPC_Matrices(A,B,Q,R,F,N)

n = size(A, 1);          % A是n*n矩阵,得到n
p = size(B, 2);          % B是n*p矩阵,得到p

% 定义M和C
M = [eye(n);                   % 初始化M矩阵,M矩阵是(N+1)n*n的, 它上面是n*n的单位矩阵,    
     zeros(N * n, n)];         % 这一步先把下半部分写成0              
C = zeros((N+1) * n, N * p);   % 初始化C矩阵,这一步令它有(N+1)n*NP个0

tmp = eye(n);                  % 定义一个n*n 的 I 矩阵
% 更新Ｍ和C
for i = 1 : N                                         % 循环,i从1到N
    rows = i * n + (1 : n);                           % 定义当前行数,从i*n开始，共n行

    C(rows, : ) = [tmp * B, C(rows-n, 1 : end - p)];  % 将c矩阵填满

    tmp = A * tmp;                                    % 每一次将tmp左乘一次A
    M(rows, : ) = tmp;                                % 将M矩阵写满
end

% 定义Q_bar和R_bar
Q_bar = kron(eye(N), Q);
Q_bar = blkdiag(Q_bar, F);
R_bar = kron(eye(N), R);

% 计算G,E,H
G = M' * Q_bar * M;             % G: n*n
E = C' * Q_bar * M;             % E: NP*n 
H = C' * Q_bar * C + R_bar;     % H：NP*NP

仿真结果：

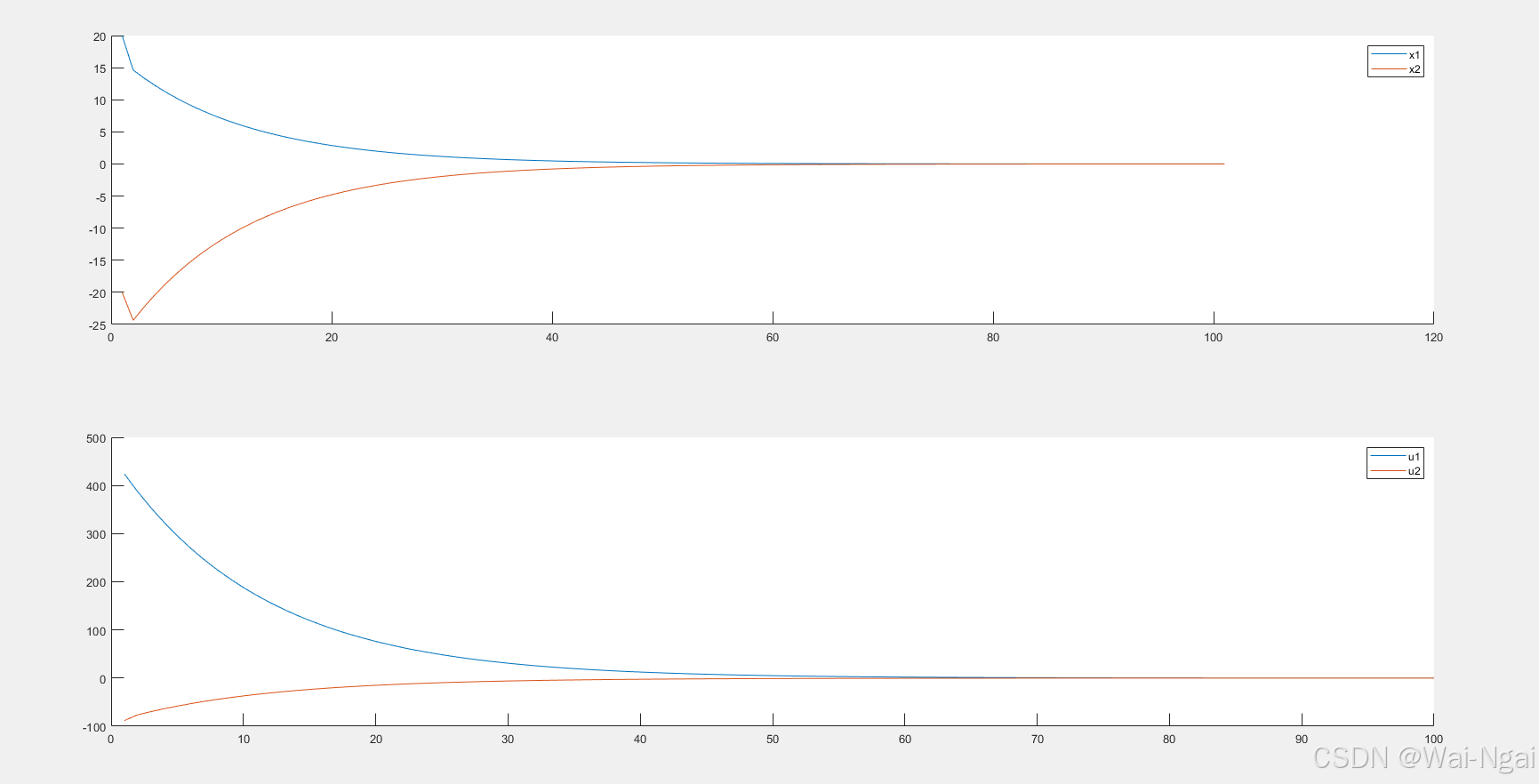
这里一共计算了100步，可以看到经过迭代，在第40步的时候，误差逐渐收敛，60步的时候状态 x 1 ， x 2 x_{1 } ，x_{2} x1，x2都接近0。

3. 最优化控制、PID、LQR、MPC

3.1 最优化控制 vs MPC

最优控制

最优控制强调的是"最优"，一般最优控制需要在整个时间域上进行求优化（这样才能保证最优性）；
最优控制常用解法：有 1变分法，2极大值原理，3动态规划；
最优控制由于过于强调最优性，而暴露出两个问题 ：
1. 对于非线性的包含复杂约束的情况难以求解；
2. 需要对系统的模型精确的知道。

MPC

模型预测控制退而求其次，仅去考虑未来几个时间步，一定程度上牺牲了最优性。
模型预测控制采用了一种折中的策略：它在每一个采样时刻，在线求解一个有限时域的最优控制问题，并只执行序列中的第一个控制动作。到下一时刻，根据新的状态测量值或估计值，重新求解优化问题，即 "滚动优化"。
这种机制带来两大核心优势：
1. 处理约束的能力：能够显式地、直接地将状态、输入、输出等各种约束纳入优化问题中。
2. 天然的反馈机制与鲁棒性：通过在每个时刻基于当前状态重新优化，MPC能够补偿模型不准确和未知扰动，其控制性能对模型精度的依赖性低于最优控制。

3.2 PID vs MPC

PID

由于各个控制回路之间存在耦合关系，多输入多输出系统的PID参数的整定变得非常困难
PID的缺点
1. PID控制器不具有"前瞻性"，在计算公式中有当前err，上个周期的err，及err累积和，但没有未来的err
2. PID是 "反应式" 控制，其输出仅依赖于过去和现在的误差，无法对未来系统的动态行为做出预判和响应。
3. PID属于无模型控制，其设计不依赖于被控对象的精确数学模型，仅通过err控制进行控制器设计；

MPC

模型预测控制善于处理多输入多输出系统
1. 对于MIMO系统，PID需要为每个子系统单独设计PID控制器，由于存在耦合对于较大的系统难以实现
模型预测控制可以处理约束
1. 安全性约束，上下阈值
模型预测控制是有向前考虑未来时间步的有限时域优化（一定的预测能力）
1. 最优控制要求在整个时间优化
2. 实际上模型预测控制采用了一个折中的策略，既不是像最优控制那样考虑这个时域，也不是完全的贪婪控制仅仅考虑当前，而是考虑未来的有限时间域。
MPC优点
- MPC是 "基于模型" 的控制，其核心是利用内部模型来预测系统未来的动态行为。
- MPC是 "预见式" 控制，它不仅能处理当前的系统状态，还能利用已知的未来信息（如设定的未来轨迹、可预知的干扰），从而提前做出优化决策，实现更平滑、更精确的控制。

3.3 LQR vs MPC

LQR

LQR是一种特殊的最优控制策略，专门针对线性系统，并以状态空间模型为基础。
它的目标函数是一个二次型代价函数，旨在最小化状态误差和控制能量消耗，最终求出一个最优的状态反馈控制律。
LQR的特点：
1. 全局最优性：与最优控制一样，LQR是在整个无限时间域上进行优化，得到一个固定的、线性的状态反馈矩阵 KK。
2. 无约束：标准的LQR理论无法直接处理对状态和输入的约束（如执行器饱和、安全限位等）。虽然在工程中可以在LQR控制律后强行加限幅，但这会破坏其最优性和理论保证。
3. 计算离线，在线高效：反馈矩阵 KK 通过求解Riccati方程离线计算完成。在线运行时，控制器只需执行一次矩阵乘法 u=−Kxu=−Kx，计算负担极轻，非常适合高速实时系统。

MPC

MPC是一种基于模型的优化控制策略，其核心是在每一个采样时刻，求解一个有限时域的开环最优控制问题。
MPC的特点：
1. 有限时域优化：与LQR的无限时域不同，MPC只对未来有限的时间步进行优化，并只执行当前时刻的控制量，在下一个时刻重新进行优化（滚动时域原理）。这牺牲了全局最优性，但获得了其他关键优势。
2. 显式处理约束：MPC最大的优势之一是能够显式地、直接地在优化问题中考虑并处理各种约束，包括控制输入约束、状态约束、输出约束等。这使得控制器的设计更贴近工程实际。
3. 模型通用性强：虽然LQR仅限于线性系统，但MPC可以自然地扩展到处理非线性系统（非线性MPC），适用性更广。
4. 在线实时优化：MPC需要在每一个控制周期内在线求解一个（可能复杂的）优化问题，这对计算硬件和算法提出了较高要求，是其应用的主要瓶颈。

核心对比

总结：LQR就是一种特殊的MPC！

4. Apollo中MPC算法

Apollo 采用MPC算法同时完成横纵向求解。整体步骤主要分为：模型预测，滚动优化，反馈控制。

代价函数：根据预测时域内，状态量的偏差，以及控制时域内，控制量的偏差计算得到的。

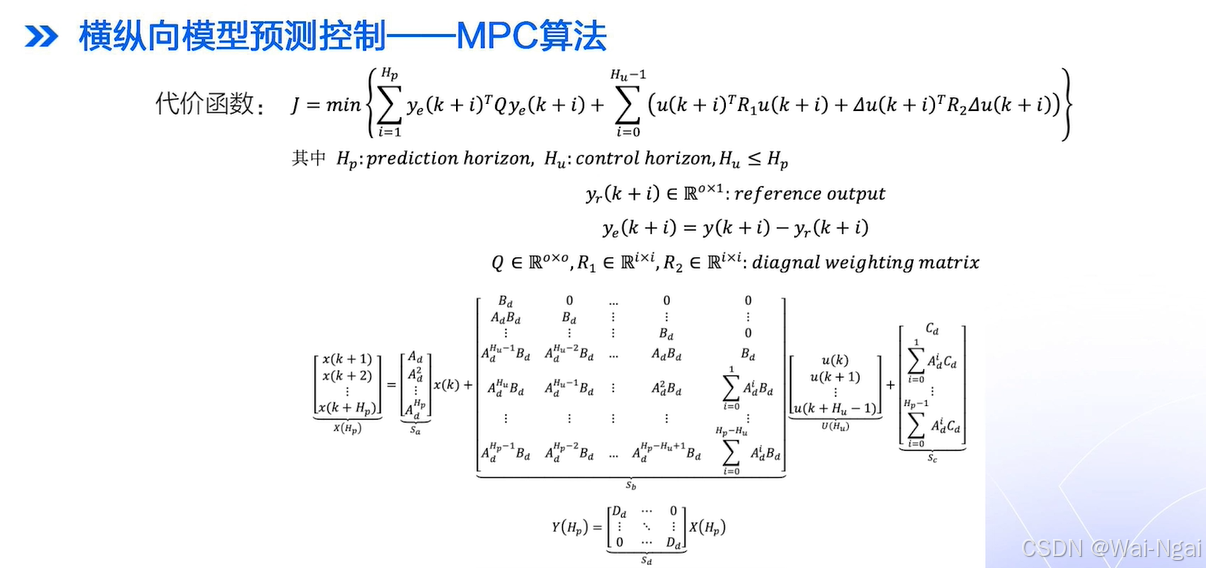
具体的算法和代码解析，可以参考博客：Apollo 9.0 控制算法 -- mpc controller

5. MPC算法使用过程中遇到的问题

MPC在实际工程应用中会遇到的核心问题。

1. 如何设置约束来加快求解？

约束是影响MPC求解速度（尤其是凸优化问题）的关键因素。不当的约束设置会大大增加计算负担。

避免冗余约束：检查你的约束条件是否存在重复或逻辑上可以被其他约束包含的情况。例如，如果一个状态变量已经被一个硬约束限制了范围，就不需要再为其设置一个更宽松的软约束。冗余约束会增加优化问题的复杂度和规模。
简化约束类型：尽量使用盒式约束，即对单个变量设置上下限。这类约束在优化算法中处理起来最高效。应尽量避免复杂的线性不等式耦合约束（如 Ax <= b 中 A 不是对角阵），如果无法避免，尽量使其稀疏。
软约束与硬约束的权衡：
- 硬约束：必须满足，但可能导致优化问题无可行解。当系统接近约束边界时，求解器可能需要更多迭代来寻找可行点。
- 软约束：通过引入松弛变量并对其施加惩罚，允许约束在必要时被轻微违反。这能保证问题的可行性，从而避免求解器因找不到可行解而报错或进行耗时的恢复操作。在保证安全的前提下，对非关键性能的约束使用软约束，可以显著提高求解速度和鲁棒性。
减少约束数量：不是所有预测时域内的点都需要施加同样严格的约束。可以考虑只在关键的几个预测步上施加约束，而不是在整个预测时域 Np 上均施加。

2. MPC可行域的设置，预测/控制时域的设置

预测时域 Np 的设置考虑因素：

系统动态响应速度 ： Np 必须足够长，以覆盖系统动态的主要部分。一个经验法则是 Np 应该至少覆盖系统的上升时间或主导时间常数的 2-3 倍。这样控制器才能"看到"其当前动作的未来后果。
稳定性与性能：理论上，对于稳定系统，Hp 越长，性能越接近无限时域的最优控制，但计算量越大。Np 过短会导致控制器"短视"，可能产生激进控制甚至不稳定。
计算负担： Np 是影响优化问题规模（决策变量数量）的首要因素。必须在性能和实时性之间权衡。

控制时域Nc 的设置及其与 Np 的关系：

控制自由度的权衡：Nc 决定了优化器可以调整未来多少步的控制动作。Nc 之后，控制量通常保持恒定（如 u(k+Nc-1)）。
Nc 与 Np 的差值：
- 通常 Nc < Np。一个常见的设置是 Nc ≈ Np / 3 到 Np / 2。
- Nc 较小（如 Nc=1或2）：决策变量少，问题简单，求解快。但控制自由度低，可能无法很好地处理复杂动态或约束，性能可能受限。
- Nc 较大（接近 Np）：控制自由度更高，能规划出更优的控制序列，性能更好，但计算量急剧增加。
经验法则：从较小的 Nc（如 3-5）开始，如果性能不满足要求，再逐步增大。确保 Nc 至少能覆盖系统响应的关键阶段。

3. 调整迭代次数及对结果的容忍度

这是在求解器层面进行"精调"和"粗调"的权衡。

最大迭代次数：
- 增加：允许求解器进行更多次搜索，更有可能找到高精度的最优解，但计算时间更长。
- 减少：可能使求解器在找到满意解之前提前终止，得到一个次优解，但计算更快。
- 策略：在调试阶段可以设置一个较大的值以确保收敛。在部署时，可以根据系统动态设置一个合理的值，例如，在系统稳态时需要的迭代次数少，在动态 transient 时需要的多。
容忍度：
- 最优性容忍度：定义了什么时候可以停止迭代。调松容忍度（增大数值）会让求解器在解还不够精确时就停止，从而显著加快求解速度，但会牺牲控制性能。在性能要求不极端的场合，这是一个非常有效的加速手段。
- 约束违反容忍度：定义了多小的违反是可以接受的。调松它也可以帮助求解器更容易地找到"可行解"。
- 建议：对于快速动态系统，可以先从较松的容忍度（如 1e-4）开始，如果控制效果不理想，再逐步收紧（如 1e-6）。

4. MPC控制器参数调节难！！终端代价

这是MPC理论的核心之一，用于弥补有限时域带来的性能损失。

终端代价函数：这是在预测时域末端对状态施加的一个惩罚项。其目的是近似无限时域的性能，告诉优化器末端状态的重要性。
终端约束集：有时会要求状态在预测时域末端进入一个特定的集合。
调节方法 ：
1. 最简单方法：将终端代价 P 设置为无限时域LQR问题的Riccati方程的解。对于稳定的线性系统，这能保证闭环稳定性，且性能接近最优。这是最常用且理论完备的方法。
2. 试凑法：如果没有理论指导，可以手动调节。通常将 P 设置为比阶段代价中的状态权重 Q 大一个数量级，以强调让状态在预测时域内回归到零或设定值。
3. 设置为零：如果不设置终端代价，相当于默认末端状态不重要。这可能导致控制器在末端"放任自流"，尤其当 Np 较短时，会引起稳定性问题。不推荐。
核心思想：终端代价/约束是连接有限时域优化和闭环稳定性/性能的桥梁。正确设置它们可以允许你使用更短的 Np，从而减少计算量。

5. 如何考虑控制器稳定性问题？

MPC的稳定性不是自动保证的，需要精心设计。

无限时域：理论上完美，但无法实现。
常用工程实践（对于稳定系统） ：
1. 足够长的预测时域 Np：如上所述，确保控制器能"看到"其动作的长期影响。
2. 终端代价 + 终端约束：这是最经典的稳定性保证方法。将终端代价 P 设为LQR的解，并假设末端之后使用LQR控制律，可以严格证明闭环稳定性。
3. 终端代价 + 无终端约束：对于开环稳定系统，仅使用一个精心设计的终端代价（如LQR的 P）而省略终端约束，在实践中通常也能获得稳定的控制，且更易于实现。
4. 收缩约束：要求每个预测时域末端的状态都比初期更接近平衡点。
实践建议：
- 对于工业应用，最稳妥的方法是：使用足够长的 Np（覆盖系统动态）并设置由LQR计算得到的终端代价 P。
- 通过仿真在不同工况和扰动下，广泛测试控制器的表现，观察状态和控制输入是否收敛、有无振荡或发散。

6. 加快MPC求解速度的方法？

这是MPC应用于快动态系统的关键。

算法层面 ：
- 使用更快的求解器：针对你的问题类型（QP， QCQP， NLP）选择高效的求解器，如 OSQP, qpOASES, IPOPT等。有些求解器对嵌入式系统做了优化。
- 热启动：将上一个控制周期求出的最优解，作为当前周期优化问题的初始猜测。由于相邻时刻的系统状态通常变化不大，最优解也非常接近，这可以极大地减少求解器所需的迭代次数。
- 显式MPC：对于线性系统、二次目标函数和线性约束的MPC，可以离线将所有可能区域的最优解预先计算好，并存储为查找表。在线计算就变成了一个简单的查表过程，速度极快。缺点是"维度灾难"，仅适用于小规模系统。
问题 formulation 层面 ：
- 降低模型阶数：用模型降阶技术获取被控对象的低阶近似模型。
- 缩短 Np 和 Nc：这是最直接有效的方法，但需注意对稳定性和性能的影响。
- 简化/减少约束：如前所述。
- 调松求解器容忍度：如前所述。
硬件层面 ：
- 使用更强大的处理器（如多核CPU、GPU）。
- 利用并行计算，因为优化算法的某些步骤（如矩阵运算）可以并行化。