【数据结构】【xjtuse】面向考纲学习（上）

我服了只能分两篇发了

ys的ds结课大预习

一部分代码搬运于 xjtuse 学长yjq @雨落俊泉

（没时间自己敲完了🤭）

也可在 Xjtuse-Guide 查看往届圣遗物

学长的代码基本照书上的来的，可以放心食用（

教材用书：数据结构与算法分析 Java版 (（美）Clifford A.Shaffer著；张铭，刘晓丹译 etc.)

考纲
知识点详解（上）
- - [1. 数据结构基本概念](#1. 数据结构基本概念)
  - - [1.1 数据、数据元素、数据项之间的关系](#1.1 数据、数据元素、数据项之间的关系)
    - [1.2 数据结构的定义](#1.2 数据结构的定义)
    - [1.3 数据结构的三要素](#1.3 数据结构的三要素)
    - [1.4 数据类型、抽象数据类型和数据结构之间的关系](#1.4 数据类型、抽象数据类型和数据结构之间的关系)
  - [2. 算法分析](#2. 算法分析)
  - - [2.1 衡量算法在资源上的两个方面](#2.1 衡量算法在资源上的两个方面)
    - [2.2 算法的渐进性分析方法以及运用该方法对算法进行评估](#2.2 算法的渐进性分析方法以及运用该方法对算法进行评估)
    - [2.3 Ο标记法以及大Ο标记法的意义](#2.3 Ο标记法以及大Ο标记法的意义)
    - [2.4 Ω标记法以及大Ω标记法的意义](#2.4 Ω标记法以及大Ω标记法的意义)
    - [2.5 Θ标记法以及大Θ标记法的意义](#2.5 Θ标记法以及大Θ标记法的意义)
    - [2.6 时空权衡原则](#2.6 时空权衡原则)
  - [3. 线性表(含栈和队列)](#3. 线性表(含栈和队列))
  - - [3.1 线性表的逻辑结构与基本操作](#3.1 线性表的逻辑结构与基本操作)
    - [3.2 顺序表](#3.2 顺序表)
    - [3.3 链式存储结构的实现技术例如单向链表及带头节点的链表](#3.3 链式存储结构的实现技术例如单向链表及带头节点的链表)
    - [3.4 链表](#3.4 链表)
    - [3.5 实际应用中不同存储结构的选取判断能力](#3.5 实际应用中不同存储结构的选取判断能力)
    - [3.6 栈与队列的逻辑结构与基本操作](#3.6 栈与队列的逻辑结构与基本操作)
    - [3.7 顺序栈和队列](#3.7 顺序栈和队列)
    - [3.8 链栈和队列](#3.8 链栈和队列)
    - [3.9 顺序存储结构中循环队列的实现具体要求](#3.9 顺序存储结构中循环队列的实现具体要求)
    - [3.10 递归调用和栈之间的关系](#3.10 递归调用和栈之间的关系)
    - [3.11 栈和队列的经典应用](#3.11 栈和队列的经典应用)
  - [4. 二叉树树和森林](#4. 二叉树树和森林)
  - - [4.1 二叉树、树和森林的定义及三者之间的异同点](#4.1 二叉树、树和森林的定义及三者之间的异同点)
    - [4.2 二叉树的四种遍历以及相关操作](#4.2 二叉树的四种遍历以及相关操作)
    - [4.3 二叉树采用顺序存储结构和链式存储结构的差异性](#4.3 二叉树采用顺序存储结构和链式存储结构的差异性)
    - - 链式二叉树的实现
    - [4.4 二叉检索树、Huffman编码树及堆的实现](#4.4 二叉检索树、Huffman编码树及堆的实现)
    - - Huffman编码树
      - [二叉搜索树 BST（Binary Search Tree）](#二叉搜索树 BST（Binary Search Tree）)
      - 堆
    - [4.5 树和森林采用的各种存储方式的差异性](#4.5 树和森林采用的各种存储方式的差异性)
    - [4.6 树和森林与二叉树的转换](#4.6 树和森林与二叉树的转换)
    - [4.7 树和森林在遍历方面与二叉树的差异及相关性](#4.7 树和森林在遍历方面与二叉树的差异及相关性)
    - [4.8 并查集的意义其两个基本操作的实现以及重量权衡平衡原则和路径压缩](#4.8 并查集的意义其两个基本操作的实现以及重量权衡平衡原则和路径压缩)
    - - [4.8.1 并查集的意义](#4.8.1 并查集的意义)
      - [4.8.2 两个基本操作](#4.8.2 两个基本操作)
      - [4.8.3 优化策略一：重量权衡平衡原则 (Weighted Union / Union by Rank)](#4.8.3 优化策略一：重量权衡平衡原则 (Weighted Union / Union by Rank))
      - [4.8.4 优化策略二：路径压缩 (Path Compression)](#4.8.4 优化策略二：路径压缩 (Path Compression))
      - [4.8.5 完整代码实现（Java版）](#4.8.5 完整代码实现（Java版）)
    - [补充：4.9 满二叉树、完全二叉树与二叉树定理](#补充：4.9 满二叉树、完全二叉树与二叉树定理)
知识点详解（下）

考纲

（来自ys）

考试时间：2025.12.6

题型

单项选择题(15分,10道题,每道题1.5分)
填空题(10分,10空,每空1分)
综合题(65分)
- 简答及证明题(6分)
- 算法渐进分析(8分)
- 递归(8分)
- 树及相关应用(BST､Huffman､Heap､树和森林､并查集)(12分)
- 图及相关应用(BFS､DFS､Topology Sort､Dijkstra以及MST)(14 分)
- 散列(7分)
- 排序(10分)
算法设计题(10分, 1题)
- 对于给定的ADT,编写满足需求的功能函数(不限编程语言)

数据结构基本概念

掌握数据､数据元素､数据项之间的关系;
掌握数据结构的定义;
掌握数据结构的三要素;
掌握数据类型､抽象数据类型和数据结构之间的关系｡

算法分析

了解衡量算法在资源上的两个方面;
掌握算法的渐进性分析方法,会用该方法对算法进行评估;
掌握Ο标记法,理解大Ο标记法的意义;
掌握Ω标记法,理解大Ω标记法的意义;
掌握Θ标记法,理解大Θ标记法的意义;
了解时空权衡原则｡

线性表(含栈和队列)

掌握线性表的逻辑结构,以及基本操作;
掌握用顺序存储结构对线性表基本操作的实现;(本部分为自学内容:在思源学堂上第4周教学页面上有教学视频)
掌握链式存储结构的实现技术,比如单向链表以及带头节点的链表;
掌握链式存储结构对线性表基本操作的实现;
具有在实际中选取不同存储结构的判断能力;
掌握栈､队列的逻辑结构,以及基本操作;
掌握顺序存储结构对栈和队列基本操作的实现;(本部分为自学内容:在思源学堂上第4周和第6周教学页面上有教学视频)
掌握链式存储结构对栈和队列基本操作的实现;(本部分为自学内容:在思源学堂上第4周和第6周教学页面上有教学视频)
掌握顺序存储结构中实现循环队列的具体要求;(本部分为自学内容:在思源学堂上第4周和第6周教学页面上有教学视频)
理解递归调用和栈之间的关系;
掌握栈和队列的经典应用｡

二叉树､树和森林

掌握二叉树､树和森林的定义以及它们之间的异同点;
掌握二叉树的四种遍历,并具有能够依赖遍历完成对二叉树进行操作的能力; (本部分为自学内容:在思源学堂上第6周教学页面上有教学视频)
理解二叉树采用顺序存储结构和链式存储结构的差异性;
掌握二叉检索树､Huffman编码以及堆的实现;
掌握树､森林采用的各种存储方式的差异性;(本部分为自学内容:在思源学堂上第8周教学页面上有教学视频)
掌握树和森林与二叉树的转换;
掌握树､森林在遍历方面和二叉树的不同以及相关性;
理解并查集的意义,以及掌握并查集的两个基本操作的实现,并掌握重量权衡平衡原则和路径压缩｡

图

掌握图的定义,包括完全图､连通图､简单路径､有向图､无向图､无环图等,明确理解图和二叉树､树和森林这种结构之间的异同点;(本部分为自学内容:通过阅读教材完成)
掌握图采用相邻矩阵和邻接表进行存储的差异性;
掌握广度优先遍历和深度优先遍历;
掌握最小支撑树(Prim算法､Kruskal算法)､最短路径(Dijkstra算法)､拓扑排序的实现过程｡

查找

理解查找的定义;
掌握对查找算法进行衡量的一些指标:平均查找长度､成功查找的查找长度､不成功查找的查找长度;
掌握顺序查找法和折半查找法,并理解二者之间的异同点;
掌握散列技术,包括散列函数､散列表､散列冲突的发生及其解决方法､以及负载因子｡(本部分为自学内容:在思源学堂上第10周教学页面上有教学视频)

排序

掌握排序的稳定性;
对直接插入排序､冒泡排序､简单选择排序､快速排序､堆排序､归并排序､基数排序这些算法,掌握具体的排序过程及排序特点,并掌握时间复杂度､空间复杂度以及是否稳定等方面的特点;
具有在不同的应用需求下,能够根据各种排序算法特点选择合适排序算法的能力｡

知识点详解（上）

（完全依照考纲版）

1. 数据结构基本概念

1.1 数据、数据元素、数据项之间的关系

数据由若干个数据元素组成，而数据元素又由若干个数据项组成。

数据：是描述客观事物的符号的集合，是信息的载体。
数据元素 ：是组成数据的的基本单位。在程序中作为整体处理。
数据项 ：是数据元素的组成部分 ，是数据中不可分割的最小单位。一个数据元素可以由若干个数据项组成。

关系总结：
数据 > 数据元素 > 数据项

举例说明：

一个班级的花名册（数据）由许多行记录组成，每一行记录对应一个学生（数据元素 ）。而每个学生的记录又包含了学号、姓名、成绩等（数据项）。

1.2 数据结构的定义

数据结构 由某一数据元素的集合以及该集合所有元素的关系组成，记为 Data_Structure = {D, R} ，D 是元素集合，R 是元素间关系的有限集合。

1.3 数据结构的三要素

一个完整的数据结构包含以下三个要素：逻辑结构、存储结构、运算。

逻辑结构
- 定义：从逻辑上描述数据元素之间的相互关系，与数据的存储无关，可以看作是抽象意义上的数据结构。
- 主要分类 ：
  - 线性结构："一对一"。例如：线性表、栈、队列。
  - 非线性结构 ：
    - 树形结构："一对多"。例如：树、二叉树。
    - 图状/网状结构："多对多"。例如：图。
存储结构
- 定义：指数据结构在计算机中的实际表示（映像），包括数据元素的表示和关系的表示。
- 主要分类 ：
  - 顺序存储：把逻辑上相邻的元素存储在物理位置上也相邻的存储单元中。优点是随机存取，缺点是可能产生碎片。例如：数组。
  - 链式存储 ：不要求逻辑上相邻的元素在物理位置上也相邻，通过附加的指针来表示元素之间的逻辑关系。优点是利用碎片空间，缺点是不能随机存取。例如：链表。
  - 索引存储：在存储元素的同时，还建立附加的索引表。通过索引可以快速定位元素。
  - 散列存储（哈希存储）：根据元素的关键字通过哈希函数直接计算出该元素的存储地址。
运算
- 运算的定义：是针对逻辑结构的，指出运算的功能。例如，对线性表定义"插入"操作。
- 运算的实现：是针对存储结构的，指出运算的具体操作步骤。例如，在顺序存储的线性表（数组）中如何实现插入，和在链式存储的线性表（链表）中如何实现插入，其具体步骤是不同的。

三要素关系 ：一种逻辑结构 可以用多种存储结构 来实现，而不同的存储结构会导致运算在实现效率上产生差异。

1.4 数据类型、抽象数据类型和数据结构之间的关系

数据类型
- 定义：是一组性质相同的值的集合以及定义在这个值集上的一组操作的总称。(一个类型和定义在该类型上的操作)
- 作用：规定了该类型变量的取值范围和所能进行的操作。例如，C语言中的 int 类型，其值集是某个区间内的整数，操作集包括加、减、乘、除、取模等。
- 本质：是程序设计语言中为了实现"信息隐藏"和"数据封装"而引入的机制。
抽象数据类型 ADT (Abstract Data Type)
- 定义：是指基于一个逻辑类型的数据类型以及这个类型上的一组操作。包含数据对象、数据关系和基本操作。
- 核心思想 ：封装和分离关切点 。ADT 将使用和实现分离。使用者只需要关心它做什么（操作），而不需要关心它怎么做（实现细节）。
- 表示：通常用 (D, S, P) 三元组表示，其中 D 是数据对象，S 是数据关系，P 是对数据的基本操作集。
- 例如："线性表"可以看作一个 ADT，它定义了 InitList, Insert, Delete, GetElem 等操作，而不管它是用数组还是链表实现的。
三者之间的关系
- 数据类型是抽象数据类型的物理基础：ADT 的概念借鉴和扩展了数据类型的思想，将其从内置类型（如int）提升到了用户自定义的复杂逻辑结构（如List, Stack）。
- 抽象数据类型是数据结构的抽象描述 ：一个 ADT 定义了一个数据结构的逻辑结构 和运算，但不涉及存储结构。例如，"栈"这个 ADT 定义了"后进先出"的逻辑特性和 push, pop 等操作。
- 数据结构是抽象数据类型的物理实现 ：当我们用某种编程语言，选择一种存储结构来实现 ADT 中定义的所有操作时，我们就得到了一个具体的数据结构。

关系总结：
数据类型 → 抽象数据类型 (ADT) → 数据结构
物理基础抽象描述物理实现数据类型抽象数据类型（ADT）数据结构角色：语言内置的基础数据封装
（如 int、char）角色：定义数据集合及操作的抽象规范
（仅描述"是什么、能做什么"）角色：遵循ADT规范，明确逻辑结构+存储结构+运算实现
（如顺序栈、链式栈）

2. 算法分析

2.1 衡量算法在资源上的两个方面

时间复杂度 ：评估算法执行所需的时间开销，即算法中所有语句的执行次数（称为频度）之和，随问题规模（通常用 n 表示）增长的变化趋势。它分析的是时间开销与问题规模之间的增长关系，而非精确的绝对时间。
空间复杂度 ：评估算法执行过程中所需占用的存储空间大小，随问题规模 n 增长的变化趋势。

总结：算法分析主要研究其时间和空间复杂度，两者都是问题规模 n 的函数，关注的是渐进增长趋势。

2.2 算法的渐进性分析方法以及运用该方法对算法进行评估

渐进性分析方法的定义 ：是算法分析的核心方法，指在算法输入规模逐渐增大时，忽略算法执行效率中的常数项、低阶项 以及具体硬件环境、数据分布等非本质因素 ，仅关注算法执行时间或空间占用 随输入规模增长的 "趋势特征"，从而客观衡量算法效率优劣的分析方法。
运用该方法进行评估的步骤
1. 抽象与简化 ：将算法中基本操作（如赋值、比较、算术运算）的执行次数表示为输入规模 n 的函数 T(n)。
2. 抓住主要矛盾 ：当 n 非常大时，函数 T(n) 中增长最快的项（最高阶项）将主导整个函数的值。常数系数和低阶项的影响变得微不足道。
3. 分类与比较 ：用渐进符号（如大O、大Θ）来描述这个增长级（如 O(n), O(n²), O(log n)），从而在宏观层面上对不同算法的效率进行清晰的分类和比较，而无需纠结于硬件差异或实现细节。

2.3 Ο标记法以及大Ο标记法的意义

Ο标记法（大O记法，渐进上界）
- 数学定义 ：如果存在正常数 c 和 n₀，使得对所有 n ≥ n₀，都有 T(n) ≤ c * f(n)，则称 T(n) 是 O(f(n)) 的。
- 通俗理解 ：大O表示算法运行时间的最坏情况增长率 ，或者说给出了函数增长的一个上界（Upper Bound） 。它告诉我们："算法的运行时间增长不会比 f(n) 更快"。
大Ο标记法的意义
1. 描述最坏情况 ：它是算法分析中最常使用的记号，因为它保证了算法的性能至少不会差于这个界限，为性能提供了一个可靠保证。
2. 用于算法选择 ：当我们说算法A是 O(n log n) 而算法B是 O(n²) 时，意味着对于大规模输入，算法A的增长速度最终将慢于算法B，因此A通常更优。

2.4 Ω标记法以及大Ω标记法的意义

Ω标记法（大Ω记法，渐进下界）
- 数学定义 ：如果存在正常数 c 和 n₀，使得对所有 n ≥ n₀，都有 T(n) ≥ c * f(n)，则称 T(n) 是 Ω(f(n)) 的。
- 通俗理解 ：大Ω表示算法运行时间的最好情况增长率 ，或者说给出了函数增长的一个下界（Lower Bound） 。它告诉我们："算法的运行时间增长至少和 f(n) 一样快"。
大Ω标记法的意义
1. 描述最优表现 ：它用于说明算法在最理想的情况下 至少需要多少时间。例如，基于比较的排序算法，其时间复杂度下界是 Ω(n log n)，这意味着不可能有 基于比较的排序算法能做得比 n log n 更好。
2. 界定问题难度：它可以帮助我们理解一个问题的固有复杂度。

2.5 Θ标记法以及大Θ标记法的意义

Θ标记法（大Θ记法，渐进紧确界）
- 数学定义 ：如果存在正常数 c₁， c₂ 和 n₀，使得对所有 n ≥ n₀，都有 c₁ * f(n) ≤ T(n) ≤ c₂ * f(n)，则称 T(n) 是 Θ(f(n)) 的。这意味着 T(n) 同时是 O(f(n)) 和 Ω(f(n))。
- 通俗理解 ：大Θ精确地描述了算法的平均或典型情况下的增长率 ，它给出了函数增长的一个紧确界（Tight Bound） 。它告诉我们："算法的运行时间增长正好和 f(n) 处于同一量级"。
大Θ标记法的意义
1. 精确描述增长级 ：当算法的最坏情况（大O）和最好情况（大Ω）的增长率相同时，我们就用大Θ来精确地描述其性能。它提供了关于算法增长率的最准确信息。
2. 表征算法稳定性 ：如果一个算法有确定的 Θ(f(n))，说明其性能对不同的输入相对稳定，不会出现极端好或极端坏的情况。例如，归并排序的时间复杂度就是 Θ(n log n)。

2.6 时空权衡原则

核心：算法的时间复杂度（执行效率）与空间复杂度（内存占用）往往相互制约，需在两者间取舍。

用空间换时间：通过增加额外存储空间（如哈希表缓存），降低时间复杂度（如查找从O(n)优化为O(1)）；
用时间换空间：通过减少额外存储，允许适度增加执行步骤（如原地排序算法，空间O(1)但时间复杂度较高）。

3. 线性表(含栈和队列)

3.1 线性表的逻辑结构与基本操作

线性表是具有相同数据类型的 n ( n ≥ 0 ) n(n≥0) n(n≥0) 个数据元素的有限序列，记为 L = ( a 0 , a 1 , . . . , a n − 1 ) L=(a_0, a_1, ..., a_{n-1}) L=(a0,a1,...,an−1)。其中：

a 0 a_0 a0 是表头元素 (head)， a n − 1 a_{n-1} an−1 是表尾元素 (tail)
每个元素都有自己的位置
除 a 0 a_0 a0 外，每个元素有且仅有一个直接前驱
除 a n − 1 a_{n-1} an−1 外，每个元素有且仅有一个直接后继
数据元素之间是一对一的线性关系

java 复制代码

public interface ListADT<E> {
    public void clear();				// 清空表
    public void append(E it);			// 在表尾添加元素
    public void insert(E it);			// 在 cur 插入元素
    public Object remove();				// 删除 cur 的值并返回该位置的元素
    public void setFirst(); 			// 将 cur 设置到表头
    public void next();					// 将 cur 后移
    public void prev();					// 将 cur 前移
    public int length();  				// 获取表实际大小
    public void setPosition(int position);	 	// 将 cur 设置为 pos
    public Object currValue(); 			// 获取 cur 的元素值
    public void setValue(E it);			// 设置 cur 的元素值
    public boolean isInList();			// 判断 cur 是否合规
    public boolean isEmpty(); 			// 判断表是否为空
    public boolean isFull();			// 判断表是否已经满了
    public void print(); 				// 打印表
}

3.2 顺序表

java 复制代码

public class SequentialList<E> implements ListADT<E> {
    private static final int DEFAULT_SIZE = 10;//默认大小

    private int maxSize;//表的最大大小
    private int numInList;//表中的实际元素数
    private int curr;//当前元素的位置
    private E[] listArray; //包含所有元素的数组

    private void setUp(int sz) {//初始化方法
        maxSize = sz;
        numInList = curr = 0;
        listArray = (E[]) new Object[sz];
    }

    public SequentialList() {//默认构造
        setUp(DEFAULT_SIZE);
    }

    public SequentialList(int maxSize) {//限制大小的构造
        setUp(maxSize);
    }

    public void clear() {
        numInList = curr = 0;//元素清空
    }

    /*在当前位置插入一个元素，从curr开始的元素全部向后移动一位
       curr上的元素变为插入的元素
     */
    public void insert(E it) {
        if (isFull()) {
            System.out.println("list is full");
            return;//表满
        } else if (curr<0||curr>numInList) {
            System.out.println("bad value for curr");
            return;//当前位置不合规
        } else {
            for (int i = numInList; i > curr; i--) {
                listArray[i] = listArray[i - 1];
            }
            listArray[curr] = it;
            numInList++;
        }
    }

    //在表尾插入一个元素
    public void append(E it) {
        if (isFull()) {
            System.out.println("list is full");
            return;//表满
        } else {
            listArray[numInList] = it;
            numInList++;
        }
    }

    //删除当前位置的值并返回该位置的元素
    public E remove() {
        if (isEmpty()) {
            System.out.println("list is empty");
            return null;
        } else if (!isInList()) {
            System.out.println("no current element");
            return null;
        } else {
            T it = listArray[curr];
            for (int i = curr; i < numInList - 1; i++) {
                listArray[i] = listArray[i + 1];//元素前移
            }
            numInList--;
            return  it;
        }
    }

    //将当前位置设置到初始位置
    public void setFirst() {
        curr = 0;
    }

    //位置前移
    public void prev() {
        curr--;
    }

    //位置后移
    public void next() {
        curr++;
    }

    //设置当前位置
    public void setPosition(int position) {
        curr = position;
    }

    //设置当前位置的元素值
    public void setValue(E it) {
        if (!isInList()) {
            System.out.println("no current element");
        } else {
            listArray[curr] = it;
        }
    }

    //获取当前位置的元素值
    public E currValue() {
        if (!isInList()) {
            System.out.println("no current element");
            return null;
        } else {
            return listArray[curr];
        }
    }

    //获取顺序表实际大小
    public int length() {
        return numInList;
    }

    //判断当前位置是否合规
    public boolean isInList() {
        return (curr >= 0 && curr < numInList);
    }

    //判断顺序表是否已经满了
    public boolean isFull() {
        return numInList >= maxSize;
    }

    //判断顺序表是否为空
    public boolean isEmpty() {
        return numInList == 0;
    }

    //打印顺序表
    public void print() {
        if (isEmpty()) {
            System.out.println("empty");
        } else {
            System.out.print("(");
            for (setFirst(); isInList(); next()) {
                System.out.print(currValue() + " ");
            }
            System.out.println(")");
        }
    }
}

3.3 链式存储结构的实现技术例如单向链表及带头节点的链表

节点结构：每个节点含 "数据域"（存储元素）和 "指针域"（指向后继节点）

单向链表：节点仅存后继指针，逻辑顺序通过指针关联，内存可分散分配

带头节点链表：增设头节点（不存有效数据），统一空表与非空表的操作逻辑，简化边界处理

3.4 链表

java 复制代码

public class Link <E> {
    //单链表结点类
    private E element;
    private Link next; //指向的下一个结点
    //构造方法
    public Link(E element, Link next) {
        this.element = element;
        this.next = next;
    }

    public Link(Link next) {
        this.next = next;
    }
    //getter和setter
    public E getElement() {
        return element;
    }

    public void setElement(E element) {
        this.element = element;
    }

    public Link getNext() {
        return next;
    }

    public void setNext(Link next) {
        this.next = next;
    }
}

java 复制代码

public class LinkedList<E> implements ListADT<E> {
    //单链表的定义
    //带有表头结点header node
    private Link<E> head;//头指针
    private Link<E> tail;//尾指针
    protected Link<E> curr;//指向当前元素前驱结点的指针


    private void setUp() {
        tail = head = curr = new Link<>(null);
    }//初始化

    //构造器
    public LinkedList() {
        setUp();
    }

    public LinkedList(int sz) {
        setUp();
    }//忽略size

    @Override
    public void clear() {  //清空所有结点
        head.setNext(null);
        curr = tail = head;
    }

    @Override
    public void insert(E it) {//在当前位置插入元素
        if (curr == null) {
            System.out.println("no current element");
            return;
        } else {
            curr.setNext(new Link(it, curr.getNext()));
            if (tail == curr) {
                tail = curr.getNext();//如果curr是尾部，则tail需要后移
            }

        }

    }

    @Override
    public void append(E it) {//在表的尾部插入元素
        tail.setNext(new Link(it, null));
        tail = tail.getNext();

    }

    @Override
    public E remove() {//删除并返回当前位置的元素值
        if (!isInList()) return null;
        E it = (E) curr.getNext().getElement();
        if (tail == curr.getNext()) tail = curr;//如果是最后一个元素，则要将尾指针前移
        curr.setNext(curr.getNext().getNext());//移除当前元素
        return it;
    }

    @Override
    public void setFirst() {//将当前位置移到开头
        curr = head;
    }

    @Override
    public void prev() {//将当前位置向前移
        if ((curr == null) || (curr == head)) {
            curr = null;
            return;
        }
        Link<E> temp = head;
        while ((temp != null) && temp.getNext() != curr) {
            temp = temp.getNext();//从头开始找，直到指针域指向curr
        }
        curr = temp;
    }

    @Override
    public void next() {//将当前位置往后移
        if (curr != null) curr = curr.getNext();
    }

    @Override
    public void setPosition(int position) {
        curr = head;
        for (int i = 0; (curr != null) && (i < position); i++) {
            curr = curr.getNext();//从头开始找
        }
    }

    @Override
    public void setValue(E it) {//设置当前位置的元素值
        if (!isInList()) {
            System.out.println("no current element");
            return;
        }
        curr.getNext().setElement(it);

    }

    @Override
    public E currValue() {//获取当前位置的元素值
       if(!isInList())return null;
       return (E) curr.getNext().getElement();
    }

    @Override
    public int length() {//获取表的实际大小
        int count=0;
        for (Link temp = head.getNext(); temp!=null ; temp=temp.getNext()) {
            count++;
        }
        return count;
    }

    @Override
    public boolean isInList() {
       return (curr!=null)&&(curr.getNext()!=null);
    }

    @Override
    public boolean isFull() {
        return false;
    }

    @Override
    public boolean isEmpty() {//判断表是否满了
        return head.getNext()==null;
    }

    @Override
    //打印表
    public void print() {
        if (isEmpty()) {
            System.out.println("empty");
        } else {
            System.out.print("(");
            for (setFirst(); isInList(); next()) {
                System.out.print(currValue() + " ");
            }
            System.out.println(")");
        }
    }
}

3.5 实际应用中不同存储结构的选取判断能力

核心判断逻辑：基于操作频率、访问方式、内存限制、容量需求四大核心因素，匹配顺序存储（顺序表）与链式存储（链表）的特性差异，具体选取标准如下：

应用场景关键词	推荐存储结构	核心原因
频繁按索引随机访问（如查第k个元素、排序后取值）	顺序表	数组下标支持O(1)随机访问，无需遍历，效率远高于链表的O(n)遍历访问
频繁在中间/头部插入/删除（如日志实时插入、队列调度）	链表（带头节点）	仅需修改指针域（O(1)操作），无需移动大量元素，规避顺序表的O(n)移动开销
内存空间紧凑、存储密度要求高（如嵌入式设备、数据量大且无频繁修改）	顺序表	无指针域开销，存储密度100%，链表因指针占用额外内存（存储密度<100%）
内存碎片多、无法分配连续大块空间（如长期运行的服务）	链表	节点分散存储，无需连续内存，顺序表需连续数组空间，易因内存碎片分配失败
容量可预测、无需频繁扩容（如固定长度的配置表）	顺序表	初始化时指定容量，避免扩容开销；链表虽无容量限制，但节点创建有额外开销
频繁尾插/尾删（如栈的基础操作、数据采集缓存）	顺序表/链表均可	顺序表尾插尾删（不扩容时）O(1)，链表尾插（记录尾节点）也O(1)，按需选择

若需"查找+修改"高频组合（如学生成绩查询与更新），优先顺序表；
若需"动态增减+遍历"高频组合（如购物车商品添加/删除），优先链表；
顺序表需注意扩容阈值（如原容量1.5倍），避免频繁扩容导致的性能波动；
链表需注意首尾节点记录（如双向链表、循环链表），优化首尾操作效率。

3.6 栈与队列的逻辑结构与基本操作

栈的基本操作

java 复制代码

public interface StackADT<E> {
    public void clear();//清空栈中所有元素
    public void push(E it);//压栈
    public E pop();//出栈
    public E topValue();//返回栈顶元素
    public boolean isEmpty();//判断栈是否空
    public void print();//打印栈中的所有元素
}

队列的基本操作

java 复制代码

public interface QueueADT <E>{
    //定义队列的抽象数据类型
    public void clear();//清空队列
    public void enqueue(E it);//入队
    public E dequeue();//出队
    public E firstValue();//；获得队首元素
    public boolean isEmpty();//判断队列是否空
    public boolean isFull();//判断队列是否为满
    public void print();//打印队列
    public int size();//获得队列中实际的元素个数
}

3.7 顺序栈和队列

顺序栈

java 复制代码

public class AStack<E> implements StackADT<E> {
    //构造顺序栈
    private final int DEFAULT_SIZE = 10;
    private int size;//栈最多能容纳的元素个数
    private int top;//可插入位置的下标
    private E[] listArray;//存储栈中元素的数组

    //初始化
    private void setUp(int size) {
        this.size = size;
        top = 0;
        listArray = (E[]) new Object[size];
    }

    //构造器
    public AStack() {
        setUp(DEFAULT_SIZE);
    }

    public AStack(int size) {
        setUp(size);
    }

    @Override
    public void clear() {
        top = 0;
    }

    @Override
    public void push(E it) {
        if (top >= size) {
            System.out.println("stack overflow");
            return;
        }
        listArray[top++] = it;
    }

    @Override
    public E pop() {
        if (isEmpty()){return null;}
        return listArray[--top];//top-1才是存储最顶元素的位置
    }

    @Override
    public E topValue() {
        if (isEmpty()){return null;}
        return listArray[top-1];
    }

    @Override
    public boolean isEmpty() {
        return top==0;
    }

    @Override
    public void print() {
        if (isEmpty()){
            System.out.println("empty");
        }
        for (int i=top-1;i>=0;i--){
            System.out.println(listArray[i]);
        }
    }
}

顺序队列

java 复制代码

public class AQueue<E> implements QueueADT<E> {
    //定义顺序队
    private static final int DEFAULT_SIZE=10;
    private int max_size;//定义队列的实际最大容纳量+1
    private int size;//队列中实际的元素个数
    private int front;//队首元素的前驱元素下标
    private int rear;//队尾元素下标
    private E[] listArray;//存储元素的下标
    
    private void setUp(int size){
        this.max_size=size+1;
        front=rear=0;
        listArray=(E[])new Object[size+1];
    }

    public AQueue() {
        setUp(DEFAULT_SIZE);
    }
    public AQueue(int size){
        setUp(size);
    }

    @Override
    public void clear() {//清空队列元素
        front=rear=0;
    }

    @Override
    public void enqueue(E it) {//进队
        if (isFull()){
            System.out.println("queue is full!");
            return;//队列已经满了
        }
        rear=(rear+1)%max_size;
        listArray[rear]=it;
        this.size++;
    }

    @Override
    public E dequeue() {//出队
        if (isEmpty()){
            System.out.println("queue is empty");
            return null;
        }
        front=(front+1)%max_size;
        size--;
        return listArray[front];
        
    }

    @Override
    public E firstValue() {
        if (isEmpty()){
            System.out.println("queue is empty");
            return null;
        }
        return listArray[(front+1)%max_size];
    }

    @Override
    public boolean isEmpty() {
        return front==rear;
    }

    @Override
    public boolean isFull() {
        return front==(rear+1)%max_size;
    }

    @Override
    public void print() {
        if (isEmpty()){
            System.out.println("queue is empty");
            return;
        }
        int temp= front+1;
        while((temp%max_size)!=rear){
            System.out.print(listArray[temp]+" ");
            temp++;
        }
        System.out.println(listArray[temp]);
    }

    @Override
    public int size() {
        return this.size;
    }
}

3.8 链栈和队列

首先定义链表

java 复制代码

public class Link <E> {
    //结点类
    private E element;
    private Link next; //指向的下一个结点
    //构造方法
    public Link(E element, Link next) {
        this.element = element;
        this.next = next;
    }

    public Link(Link next) {
        this.next = next;
    }
    //getter和setter
    public E getElement() {
        return element;
    }

    public void setElement(E element) {
        this.element = element;
    }

    public Link getNext() {
        return next;
    }

    public void setNext(Link next) {
        this.next = next;
    }
}

链栈

java 复制代码

public class LStack<E> implements StackADT<E> {
    private Link<E> top;//栈顶元素

    //初始化与构造器
    private void setUp() {
        top = null;
    }

    public LStack() {
        setUp();
    }

    public LStack(int size) {
        setUp();
    }

    @Override
    public void clear() {
        top = null;
    }

    @Override
    public void push(E it) {
        top = new Link<E>(it, top);
    }

    @Override
    public E pop() {
        if (isEmpty()) {
            System.out.println("stack is empty");
            return null;
        }
        E it = top.getElement();
        top = top.getNext();
        return it;
    }

    @Override
    public E topValue() {
        if (isEmpty()) {
            System.out.println("no top value");
            return null;
        }
        return top.getElement();
    }

    @Override
    public boolean isEmpty() {
        return top == null;
    }

    @Override
    public void print() {
        if (isEmpty()) {
            System.out.println("empty");
            return;
        }
        Link<E> temp = top;
        while (temp != null) {
            System.out.println(temp.getElement());
            temp = temp.getNext();
        }
    }
}

链队列

java 复制代码

public class LQueue<E> implements QueueADT<E> {
    private Link<E> front;//指向队首元素的指针
    private Link<E> rear;//指向队尾元素的指针
    private int size=0;//队列中实际的元素个数

    private void setUp() {
        front = rear = null;
    }

    public LQueue() {
        setUp();
    }

    public LQueue(int size) {
        setUp();
    }

    @Override
    public void clear() {
        front = rear = null;
    }

    @Override
    public void enqueue(E it) {//进队
        if (isEmpty()) {
            front = rear = new Link<E>(it, null);//队列为空
        } else {
            rear.setNext(new Link<E>(it, null));
            rear = rear.getNext();//尾指针后移
        }
        size++;

    }

    @Override
    public E dequeue() {//出队
        if (isEmpty()) {
            System.out.println("queue is empty");
            return null;
        }
        E it = front.getElement();
        front = front.getNext();
        if (front == null) rear = null;//如果队空了，也要将尾指针设为null
        size--;
        return it;
    }

    @Override
    public E firstValue() {
        if (isEmpty()) {
            System.out.println("queue is empty");
            return null;
        }
        return front.getElement();
    }

    @Override
    public boolean isEmpty() {
        return front == null;
    }

    @Override
    public boolean isFull() {
        return false;
    }

    @Override
    public void print() {
        if (isEmpty()) {
            System.out.println("queue is empty");
            return;
        }
        Link<E> temp = front;
        if (temp == rear) {
            System.out.println(temp.getElement());
            return;
        }
        while (temp != rear) {
            System.out.print(temp.getElement() + " ");
            temp = temp.getNext();
        }
        System.out.println(temp.getElement());
    }

    @Override
    public int size() {
        return size;
    }
}

3.9 顺序存储结构中循环队列的实现具体要求

存储基础：基于数组实现，通过"循环复用数组空间"避免普通顺序队列的"假溢出"问题
核心设计要求
1. 指针定义：front（队首指针，指向队首元素）、rear（队尾指针，指向队尾元素的下一个空位置）
2. 判空与判满设计：判空 front == rear，判满 (rear + 1) % size == front
3. 容量设计：数组容量固定（或支持扩容），初始化时指定最大容量
基本操作要求：
- 入队：先判满，再将元素存入rear位置，rear = (rear + 1) % size
- 出队：先判空，再取出front位置元素，front = (front + 1) % size
- 取队首：判空后直接返回数组[front]，不移动指针
- 清空：front = rear = 0（或 size = 0）

其实就是在普通的顺序队列的所有操作加上取模

3.10 递归调用和栈之间的关系

核心关联：递归调用的执行机制完全依赖"栈"（称为"递归栈"），栈是递归实现的底层支撑
具体对应关系：
- 递归调用 ⇔ 入栈操作
- 递归返回 ⇔ 出栈操作
- 递归深度 ⇔ 栈的最大深度
- 执行顺序：递归调用顺序 → 栈的入栈顺序；递归返回顺序 → 栈的出栈顺序（LIFO特性匹配）
关键注意：递归深度过大会导致"栈溢出"（栈空间不足）

底层依赖递归调用机制栈（递归栈）递归调用时封装当前函数栈帧
（参数+返回地址+局部变量）栈帧压入递归栈递归返回时栈顶栈帧弹出恢复上一层函数执行环境
（参数+局部变量+返回地址）继续执行上一层函数

实例：计算 n! 的递归调用

// 计算factorial(3)时的调用栈变化：
// 初始：空栈
// 调用factorial(3): 压入(3, 返回地址)
// 调用factorial(2): 压入(2, 返回地址)
// 调用factorial(1): 压入(1, 返回地址) - 递归基
// 返回1: 弹出factorial(1)的信息
// 返回2: 弹出factorial(2)的信息
// 返回6: 弹出factorial(3)的信息
任何递归算法都可以通过显式栈转换为非递归算法

java 复制代码

// 递归版本的深度优先遍历
public void dfsRecursive(Node node) {
    if (node == null) return;
    visit(node);
    dfsRecursive(node.left);
    dfsRecursive(node.right);
}

// 非递归版本使用显式栈
public void dfsIterative(Node root) {
    if (root == null) return;
    Stack<Node> stack = new Stack<>();
    stack.push(root);
    
    while (!stack.isEmpty()) {
        Node node = stack.pop();
        visit(node);
        if (node.right != null) stack.push(node.right);
        if (node.left != null) stack.push(node.left);
    }
}

3.11 栈和队列的经典应用

栈的经典应用（基于LIFO：后进先出特性）
1. 括号匹配校验（如LeetCode 20题）：左括号入栈，右括号与栈顶左括号匹配则出栈，最终栈空则合法
2. 表达式求值（前缀/中缀/后缀表达式）：中缀转后缀用栈存储运算符，后缀求值用栈存储操作数
3. 函数调用栈：JVM中方法递归/嵌套调用时，用栈保存方法栈帧（参数、返回地址等）
4. 深度优先搜索（DFS）：用栈存储待访问节点，回溯时弹出节点，遍历图/树的所有路径
5. 浏览器前进后退功能：两个栈分别存储"前进历史"和"后退历史"，切换时转移栈中元素
队列的经典应用（基于FIFO：先进先出特性）
1. 广度优先搜索（BFS）：用队列存储待访问节点，按层级遍历图/树（如二叉树层序遍历、最短路径求解）
2. 任务调度（如线程池、消息队列）：按提交顺序依次执行任务，避免任务抢占导致的无序问题
3. 缓冲队列（如IO缓冲、网络数据传输）：暂时存储突发的大量数据，按顺序处理，缓解处理模块压力
4. 生产者-消费者模型：队列作为数据缓冲区，生产者入队数据，消费者出队数据，解耦生产与消费节奏
5. 循环队列的实际应用：打印机任务队列、网络请求排队处理（利用循环复用空间的高效特性）

4. 二叉树树和森林

4.1 二叉树、树和森林的定义及三者之间的异同点

二叉树（Binary Tree） ：n（n≥0）个节点的有限集合，每个节点最多有两个子树（左子树、右子树），子树有左右顺序之分
树（Tree） ：n（n≥0）个节点的有限集合，存在唯一 "根节点"，其余节点划分为互不相交的子树（n=0 时为空树），子树之间没有次序关系。
森林（Forest）：m（m≥0）棵互不相交的树的集合（m=0 时为空森林，单棵树可视为 m=1 的森林）

三者之间的异同点：

特征	二叉树	树	森林
结点度数	每个结点最多2度（0,1,2）	每个结点度数无限制	每棵树的结点度数无限制
子树次序	左、右子树有严格次序	子树无次序关系	树与树之间无次序关系
基本结构	递归定义为根+左子树+右子树	递归定义为根+子树集合	多棵互不相交的树
空结构	允许空二叉树（n=0）	允许空树（n=0）	允许空森林（m=0）
相互关系	树的特例	森林加根成为树，树去根成为森林	树的集合

4.2 二叉树的四种遍历以及相关操作

二叉树节点定义：

java 复制代码

class TreeNode<T> {
    T val;
    TreeNode<T> left;
    TreeNode<T> right;
    public TreeNode(T val) {
        this.val = val;
        this.left = null;
        this.right = null;
    }
}

前序遍历（根→左→右）

java 复制代码

// 递归版
public void preOrder(TreeNode<T> root, List<T> result) {
    if (root == null) return;
    result.add(root.val); // 访问根
    preOrder(root.left, result); // 遍历左子树
    preOrder(root.right, result); // 遍历右子树
}

中序遍历（左→根→右）

java 复制代码

// 递归版
public void inOrder(TreeNode<T> root, List<T> result) {
    if (root == null) return;
    inOrder(root.left, result); // 遍历左子树
    result.add(root.val); // 访问根
    inOrder(root.right, result); // 遍历右子树
}

后序遍历（左→右→根）

java 复制代码

// 递归版
public void postOrder(TreeNode<T> root, List<T> result) {
    if (root == null) return;
    postOrder(root.left, result); // 遍历左子树
    postOrder(root.right, result); // 遍历右子树
    result.add(root.val); // 访问根
}

层序遍历（按层级从左到右，基于队列实现）

java 复制代码

public void levelOrder(TreeNode<T> root, List<T> result) {
    if (root == null) return;
    Queue<TreeNode<T>> queue = new LinkedList<>();
    queue.offer(root);
    while (!queue.isEmpty()) {
        TreeNode<T> node = queue.poll();
        result.add(node.val); // 访问当前层节点
        if (node.left != null) queue.offer(node.left); // 左孩子入队
        if (node.right != null) queue.offer(node.right); // 右孩子入队
    }
}

核心操作

求二叉树节点总数（后序遍历）

java 复制代码

public int countNodes(TreeNode<T> root) {
    if (root == null) return 0;
    // 1. 先遍历左子树，求左子树节点数（左）
    int leftCount = countNodes(root.left);
    // 2. 再遍历右子树，求右子树节点数（右）
    int rightCount = countNodes(root.right);
    // 3. 最后处理根：当前树的节点数 = 左 + 右 + 1（根自己）（处理根）
    return leftCount + rightCount + 1;
}

前序遍历版：

java 复制代码

// 前序版求节点总数（逻辑能跑，但顺序变了）
public int countNodesPre(TreeNode<T> root) {
    if (root == null) return 0;
    // 1. 先处理根：计数+1（处理根）
    int count = 1;
    // 2. 遍历左子树，累加左子树节点数（左）
    count += countNodesPre(root.left);
    // 3. 遍历右子树，累加右子树节点数（右）
    count += countNodesPre(root.right);
    return count;
}

求二叉树深度（后序遍历）

java 复制代码

public int treeDepth(TreeNode<T> root) {
    if (root == null) return 0;
    // 1. 遍历左子树，求左子树深度（左）
    int leftDepth = treeDepth(root.left);
    // 2. 遍历右子树，求右子树深度（右）
    int rightDepth = treeDepth(root.right);
    // 3. 处理根：当前树深度 = 左右子树最大深度 + 1（根自己的层）（处理根）
    return Math.max(leftDepth, rightDepth) + 1;
}

查找指定值节点（前序遍历）

java 复制代码

public TreeNode<T> findNode(TreeNode<T> root, T target) {
    if (root == null) return null;
    // 1. 先处理根：检查当前根是不是要找的目标（处理根）
    if (root.val.equals(target)) return root;
    // 2. 根不是，遍历左子树找（左）
    TreeNode<T> leftFind = findNode(root.left, target);
    if (leftFind != null) return leftFind;
    // 3. 左子树没找到，遍历右子树找（右）
    return findNode(root.right, target);
}

构建二叉树（基于前序+中序遍历结果）

java 复制代码

public TreeNode<Integer> buildTree(int[] preOrder, int[] inOrder) {
    if (preOrder.length == 0 || inOrder.length == 0) return null;
    // 前序第一个元素为根节点
    TreeNode<Integer> root = new TreeNode<>(preOrder[0]);
    // 找到中序中根节点的索引，划分左右子树
    int rootIdx = 0;
    for (int i = 0; i < inOrder.length; i++) {
        if (inOrder[i] == root.val) {
            rootIdx = i;
            break;
        }
    }
    // 递归构建左右子树
    root.left = buildTree(Arrays.copyOfRange(preOrder, 1, rootIdx + 1),
                          Arrays.copyOfRange(inOrder, 0, rootIdx));
    root.right = buildTree(Arrays.copyOfRange(preOrder, rootIdx + 1, preOrder.length),
                           Arrays.copyOfRange(inOrder, rootIdx + 1, inOrder.length));
    return root;
}

验证二叉搜索树（中序遍历特性：结果递增）

java 复制代码

private TreeNode<Integer> prev = null;
public boolean isValidBST(TreeNode<Integer> root) {
    if (root == null) return true;
    // 1. 先遍历左子树，校验左子树是否合法（左）
    if (!isValidBST(root.left)) return false;
    // 2. 处理根：校验当前根是否比前一个节点大（中序遍历结果要递增）（处理根）
    if (prev != null && root.val <= prev.val) return false;
    prev = root; // 记录当前根，作为下一个节点的"前一个节点"
    // 3. 再遍历右子树，校验右子树是否合法（右）
    return isValidBST(root.right);
}

遍历方式的选择依据：

需要先访问父结点再访问子结点时使用前序遍历
需要按照排序顺序访问二叉搜索树时使用中序遍历
需要先处理子结点再处理父结点时使用后序遍历
需要按层级处理结点时使用层次遍历

4.3 二叉树采用顺序存储结构和链式存储结构的差异性

顺序存储结构：以数组为底层载体，按"层序遍历顺序"存储二叉树节点，通过数组索引映射节点的父子关系，空节点需占用数组位置（或用特殊值标记）。
链式存储结构：以节点为基本单元（每个节点含"数据域"+"左指针域"+"右指针域"），节点间通过指针关联父子关系，内存可分散分配，空指针表示无左/右子树。

对比维度	顺序存储结构	链式存储结构
存储逻辑	依赖数组索引映射父子关系，物理存储连续	依赖指针关联父子关系，物理存储分散
适用二叉树类型	完全二叉树/满二叉树（空间无浪费）	任意二叉树（含斜树、稀疏二叉树）
空间利用率	完全二叉树：100%；普通二叉树：大量空闲位置（浪费严重）	仅存储有效节点+指针，无空闲浪费，空间利用率高
访问节点效率（父/子）	O(1)（通过索引直接计算，无需遍历）	O(n)（需从根节点开始遍历查找目标节点）
插入/删除节点效率	O(n)（可能需移动数组元素，或扩容）	O(1)（找到目标节点后，仅需修改指针）
扩容/伸缩性	固定容量（需提前分配），扩容需复制数组	动态伸缩（按需创建/释放节点），无扩容开销
空节点处理	占用数组位置（或特殊值标记）	指针置空，不占用额外空间
实现复杂度	简单（无需处理指针，仅数组操作）	稍复杂（需管理指针，避免空指针异常）
内存要求	需连续大块内存（数组特性）	无需连续内存，支持分散分配

顺序存储的"索引映射规则"：仅适用于完全二叉树，若为普通二叉树（如斜树），数组会出现大量空闲位置（例如斜树 n n n 个节点，需占用数组 2 n − 1 2^{n-1} 2n−1 个位置），空间浪费极严重。
链式存储的扩展能力：支持灵活扩展为"三叉链表"（增加"父指针域"），方便回溯父节点（如二叉树遍历中的回溯操作），而顺序存储无法直接支持该扩展。
操作效率的核心差异：顺序存储的优势是"随即访问"（如快速获取第k层第m个节点），链式存储的优势是"动态修改"（如插入新节点、删除叶子节点）。
实际应用场景：顺序存储常用于堆排序（基于完全二叉树的堆结构）、优先队列；链式存储常用于二叉树遍历、动态构建任意结构二叉树（如表达式树、搜索树）。

顺序存储：
0 1 2 3 4 7 8 9 10 5 6 11

对于节点 r r r

parent(r) = (r - 1) / 2 (0<r<n)
leftchild(r) = 2r + 1 (2r+1<n)
rightchild(r) = 2r + 2 (2r+2<n)
leftsibling(r) = r - 1 (r 为偶数且 0<r<n)
rightsibling(r) = r + 1 (r 为奇数且 r+1<n)

结点	0	1	2	3	4	5	6	7	8	9	10	11
父结点	--	0	0	1	1	2	2	3	3	4	4	5
左子结点	1	3	5	7	9	11	--	--	--	--	--	--
右子结点	2	4	6	8	10	--	--	--	--	--	--	--
左兄弟结点	--	--	1	--	3	--	5	--	7	--	9	--
右兄弟结点	--	2	--	4	--	6	--	8	--	10	--	--

链式二叉树的实现

结点类

java 复制代码

public class BinNodePtr {
    //链式二叉树的结点类
    private Object element;		//存储数据的元素
    private BinNodePtr left;	//左子结点
    private BinNodePtr right;	//右子结点

    //constructor部分
    public BinNodePtr(){}
    public BinNodePtr(Object element){this.element = element;}
    public BinNodePtr(Object element, BinNodePtr l, BinNodePtr r){
    	this.element = element;
		left = l; right = r;
	}

    //getter与setter部分
    public Object getElement() {return element;}
    public void setElement(Object element) {this.element = element;}

    public BinNodePtr getLeft() {return left;}
    public void setLeft(BinNodePtr left) {this.left = left;}

    public BinNodePtr getRight() {return right;}
    public void setRight(BinNodePtr right) {this.right = right;}
    
    public boolean isLeaf() {
        return (left == null) && (right == null);
    }		
   
    public String toString() {
        return "BinNodePtr{" +
                "element=" + element +
                '}';
    }
}

4.4 二叉检索树、Huffman编码树及堆的实现

Huffman编码树

Huffman编码：一种不等长编码。高频字符用短码，低频用长码，保证无歧义，且总编码长度最短。

基本概念
- 路径长度：从根结点到某结点所经过的边数。
- 外部路径长度 ：树中所有叶子结点到根节点的路径长度之和。
- 内部路径长度 ：树中所有非叶子结点到根节点的路径长度之和。
- 带权路径长度 ：树中所有 叶子结点的权值 × \times ×到根节点的路径之和。
Huffman编码树的构建流程
1. 根据给定的n个权值{W₁, W₂..., Wₙ}，构造n棵二叉树的集合F = {T₁, T₂,..., Tₙ}，其中每棵二叉树中均只含一个带权值为Wᵢ的根结点，其左、右子树为空树；
2. 在F中选取其根结点的权值为最小（通过 hufflist 维护）的两棵二叉树，分别作为左、右子树构造一棵新的二叉树，并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和；
3. 从F中删去这两棵树，同时加入刚生成的新树；
4. 重复(2)和(3)两步，直至F中只含一棵树为止
图解样例 happy every weekend （忽略空格）

步骤0：初始状态

初始列表按权重排序：h:1, a:1, v:1, r:1, w:1, k:1, n:1, d:1, p:2, y:2, e:5

h:1 a:1 v:1 r:1 w:1 k:1 n:1 d:1 p:2 y:2 e:5

步骤1：合并h(1)和a(1)

移除h和a，合并为(h+a):2，插入到p:2之前
v:1 r:1 w:1 k:1 n:1 d:1 h+a:2 h:1 a:1 p:2 y:2 e:5

步骤2：合并v(1)和r(1)

移除v和r，合并为(v+r):2，插入到p:2之前
w:1 k:1 n:1 d:1 h+a:2 h:1 a:1 v+r:2 v:1 r:1 p:2 y:2 e:5

步骤3：合并w(1)和k(1)

移除w和k，合并为(w+k):2，插入到p:2之前
n:1 d:1 h+a:2 h:1 a:1 v+r:2 v:1 r:1 w+k:2 w:1 k:1 p:2 y:2 e:5

步骤4：合并n(1)和d(1)

移除n和d，合并为(n+d):2，插入到p:2之前
h+a:2 h:1 a:1 v+r:2 v:1 r:1 w+k:2 w:1 k:1 n+d:2 n:1 d:1 p:2 y:2 e:5

步骤5：合并p(2)和y(2)

移除p和y，合并为(p+y):4，插入到e:5之前
h+a:2 h:1 a:1 v+r:2 v:1 r:1 w+k:2 w:1 k:1 n+d:2 n:1 d:1 p+y:4 p:2 y:2 e:5

步骤6：合并(h+a)(2)和(v+r)(2)

移除(h+a)和(v+r)，合并为(h+a+v+r):4，插入到e:5之前
w+k:2 w:1 k:1 n+d:2 n:1 d:1 p+y:4 p:2 y:2 h+a+v+r:4 h+a:2 v+r:2 h:1 a:1 v:1 r:1 e:5

步骤7：合并(w+k)(2)和(n+d)(2)

移除(w+k)和(n+d)，合并为(w+k+n+d):4，插入到e:5之前（权重4<5）
p+y:4 p:2 y:2 h+a+v+r:4 h+a:2 v+r:2 h:1 a:1 v:1 r:1 w+k+n+d:4 w+k:2 n+d:2 w:1 k:1 n:1 d:1 e:5

步骤8：合并(p+y)(4)和(h+a+v+r)(4)

移除(p+y)和(h+a+v+r)，合并为(p+y+h+a+v+r):8，插入到e:5之后（权重8>5）
w+k+n+d:4 w+k:2 n+d:2 w:1 k:1 n:1 d:1 e:5 p+y+h+a+v+r:8 p+y:4 h+a+v+r:4 p:2 y:2 h+a:2 v+r:2 h:1 a:1 v:1 r:1

步骤9：合并(w+k+n+d)(4)和e(5)

移除(w+k+n+d)和e，合并为(e+w+k+n+d):9，插入到(p+y+h+a+v+r):8之后（权重9>8）
p+y+h+a+v+r:8 p+y:4 h+a+v+r:4 p:2 y:2 h+a:2 v+r:2 h:1 a:1 v:1 r:1 e+w+k+n+d:9 e:5 w+k+n+d:4 w+k:2 n+d:2 w:1 k:1 n:1 d:1

步骤10：合并(p+y+h+a+v+r)(8)和(e+w+k+n+d)(9)

移除最后两个元素，合并为最终Huffman树(根:17)
根:17 p+y+h+a+v+r:8 e+w+k+n+d:9 p+y:4 h+a+v+r:4 p:2 y:2 h+a:2 v+r:2 h:1 a:1 v:1 r:1 e:5 w+k+n+d:4 w+k:2 n+d:2 w:1 k:1 n:1 d:1

代码实现

java 复制代码

// 字母-频率配对类：存储单个字符及其出现频率
class LettFreq { 
    private char lett;  // 存储的字母
    private int freq;   // 该字母的出现频率

    // 构造方法1：初始化字母和对应的频率
    public LettFreq(int f, char l) { 
        freq = f; 
        lett = l; 
    }

    // 构造方法2：仅初始化频率（用于哈夫曼树的中间节点，无实际字母）
    public LettFreq(int f) { 
        freq = f; 
    }

    // 返回当前对象的频率（作为哈夫曼树节点的权重）
    public int weight() { 
        return freq; 
    }

    // 返回当前对象对应的字母
    public char letter() { 
        return lett; 
    }
} // end class LettFreq

java 复制代码

// 哈夫曼树类：表示一棵哈夫曼编码树
class HuffTree { 
    private BinNode root;  // 哈夫曼树的根节点（BinNode是二叉树节点的自定义类型）

    // 构造方法1：创建仅含一个节点的哈夫曼树（对应哈夫曼树初始的"单节点树"）
    public HuffTree(LettFreq val) {
        // BinNodePtr是BinNode的实现类，这里用val初始化根节点
        root = new BinNodePtr(val); 
    }

    // 构造方法2：合并两棵哈夫曼树，创建新的哈夫曼树
    // 参数：val（新根节点的字母-频率）、l（左子树）、r（右子树）
    public HuffTree(LettFreq val, HuffTree l, HuffTree r) {
        // 新根节点的元素是val，左孩子是左子树的根，右孩子是右子树的根
        root = new BinNodePtr(val, l.root(), r.root()); 
    }

    // 返回哈夫曼树的根节点
    public BinNodePtr root() { 
        return root; 
    }

    // 返回哈夫曼树的权重（即根节点的权重，哈夫曼树权重=根节点权重）
    public int weight() { 
        // 根节点的元素是LettFreq类型，强转后取weight
        return ((LettFreq)root.element()).weight(); 
    }
} // end class HuffTree

java 复制代码

// 从哈夫曼树列表构建最终哈夫曼树的静态方法
// 参数：hufflist是有序列表（按哈夫曼树权重从小到大排序）
static HuffTree buildTree(List hufflist) {
    HuffTree temp1, temp2, temp3;  // 临时变量：存储取出的两棵树、合并后的新树
    LettFreq tempnode;             // 临时变量：存储新树的根节点（字母-频率）

    // 循环条件：列表中至少有两个元素（需要合并操作）
    // setPos(1)：将列表指针设为1（可能是确保列表有多个元素的判断逻辑）
    for(hufflist.setPos(1); hufflist.isInList(); hufflist.setPos(1)) {
        hufflist.setFirst();        // 将列表指针移到第一个元素
        temp1 = (HuffTree)hufflist.remove();  // 取出列表中第一个树（权重最小）
        temp2 = (HuffTree)hufflist.remove();  // 取出列表中第二个树（权重次小）
        
        // 新建LettFreq：权重是两棵树的权重之和（无实际字母，用于中间节点）
        tempnode = new LettFreq(temp1.weight() + temp2.weight());
        // 合并temp1和temp2为新树temp3：新树根是tempnode，左子树temp1，右子树temp2
        temp3 = new HuffTree(tempnode, temp1, temp2);

        // 将新树temp3按权重有序插入列表（保持列表从小到大排序）
        for (hufflist.setFirst(); hufflist.isInList(); hufflist.next()) {
            // 找到第一个权重≥temp3的位置，插入temp3
            if (temp3.weight() <= ((HuffTree)(hufflist.currValue())).weight()) {
                hufflist.insert(temp3); 
                break; 
            }
        }
        // 如果遍历完列表都没找到（temp3是权重最大的），则追加到列表末尾
        if (!hufflist.isInList()) {
            hufflist.append(temp3);
        }
    }
    hufflist.setFirst();            // 列表只剩最后一棵树，指针移到第一个元素
    return (HuffTree)hufflist.remove();  // 返回最终的哈夫曼树
}

0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 根:17 p+y+h+a+v+r:8 e+w+k+n+d:9 p+y:4 h+a+v+r:4 p:2 y:2 h+a:2 v+r:2 h:1 a:1 v:1 r:1 e:5 w+k+n+d:4 w+k:2 n+d:2 w:1 k:1 n:1 d:1

左子节点连的边标0，右子节点连的边标1，从根到子节点的路径（外部路径）即所有字符的编码：

复制代码

p: 000
y: 001
h: 0100
a: 0101
v: 0110
r: 0111
e: 10
w: 1100
k: 1101
n: 1110
d: 1111

二叉搜索树 BST（Binary Search Tree）

BST：任意节点左子树所有节点值 < 该节点值 < 右子树所有节点值。

使用中序排序打印所有节点将得到从小到大的排序。
37 24 42 7 32 2 40 42 120

BST 的 ADT

java 复制代码

public interface BSTADT <K extends Comparable<K>, V> {
    public void insert(K key, V value);//插入结点
    public V remove(K key);//根据key值删除结点
    public boolean update(BinNode<K, V> rt, K key, V value);//更新结点值
    public V search(K key);//搜索key所对应结点的value
    public int getHeight(BinNode<K, V> rt);//获得树高
    public boolean isEmpty();//判断是否为空
    public void clear();//清空树
}

BST 的结点类

java 复制代码

public class BinNode<K extends Comparable<K>, V> {
    private K key;
    private V value;

    private BinNode<K, V> left;
    private BinNode<K, V> right;

    public BinNode(K key, V value){
        left = right = null;
        this.key=key;
        this.value=value;
    }
    public BinNode() {left = right = null;}

    public boolean isLeaf() {return (left == null) && (right == null);}

    public K getKey() {return key;}
    public void setKey(K key) {this.key = key;}

    public V getValue() {return value;}
    public void setValue(V value) {this.value = value;}

    public BinNode<K, V> getLeft() {return left;}
    public void setLeft(BinNode<K, V> left) {this.left = left;}

    public BinNode<K, V> getRight() {return right;}
    public void setRight(BinNode<K, V> right) {this.right = right;}
}

java 复制代码

/**
 * @author yjq
 * @version 1.0
 * @date 2021/11/20 22:51
 */

public class BinarySearchTree<K extends Comparable<K>, V> implements BSTADT<K, V> {
    private BinNode<K, V> root;
    private V removeValue;

    public BinarySearchTree() {
        root = null;
    }

    public BinNode<K, V> getRoot() {
        return root;
    }

    public void insert(K key, V value) {
        try {
            if (key == null) {
                throw new Exception("Key is null, insert fault!");
            }
            if (value == null) {
                throw new Exception("Value is null, insert fault!.");
            }
        } catch (Exception e) {
            e.printStackTrace();
        }
        root = insertHelp(root, key, value);
    }

    private BinNode<K, V> insertHelp(BinNode<K, V> rt, K key, V value) {
        if (rt == null) {
            return new BinNode<K, V>(key, value);
        }

        if (key.compareTo(rt.getKey()) < 0) {
            rt.setLeft(insertHelp(rt.getLeft(), key, value));
        }//跟删除结点有异曲同工之妙

        else if (key.compareTo(rt.getKey()) > 0) {
            rt.setRight(insertHelp(rt.getRight(), key, value));
        }

        else {
            rt.setValue(value);
        }//key值相同则更新
        return rt;
    }

    /**
     *
     * @param key 关键字
     * @return 删除的结点的值
     */
    public V remove(K key) {
        removeValue = null;
        try {
            if (key == null)
                throw new Exception("Key is null, remove failure");
            root = removeHelp(root, key);
            return removeValue;
        } catch (Exception e) {
            e.printStackTrace();
            return null;
        }
    }

    private BinNode<K, V> removeHelp(BinNode<K, V> rt, K key) {
        if (rt == null)
            return null;
        if (key.compareTo(rt.getKey()) < 0) {
            rt.setLeft(removeHelp(rt.getLeft(), key));
        } else if (key.compareTo(rt.getKey()) > 0) {
            rt.setRight(removeHelp(rt.getRight(), key));
        } else {
            if (rt.getLeft() == null) {
                removeValue = rt.getValue();
                rt = rt.getRight();
                //左子结点为空，直接将右子结点作为当前根结点
            } else if (rt.getRight() == null) {
                removeValue = rt.getValue();
                rt = rt.getLeft();
                //右子结点为空，直接将左子结点作为当前根结点
            } else {
                //待删除结点有两个子结点
                rt.setKey((K) getMinNode(rt.getRight()).getKey());
                rt.setValue((V) getMinNode(rt.getRight()).getValue());
                //将当前结点的key和value更新为右子树中的最小结点的值
                rt.setRight(removeMinNode(rt.getRight()));
                //将当前结点的右子结点进行更新
            }
        }
        return rt;
    }

    private BinNode getMinNode(BinNode<K, V> rt) {
        if (rt.getLeft() == null)
            return rt;
        else
            return getMinNode(rt.getLeft());
    }

    //返回的是更新以后的根结点
    private BinNode<K, V> removeMinNode(BinNode<K, V> rt) {
        if (rt.getLeft() == null) {
            return rt.getRight();
        }
        rt.setLeft(removeMinNode(rt.getLeft()));
        //保证了二叉检索树的规范性
        return rt;
    }

    public V search(K key) {
        return search(root, key);
    }

    private V search(BinNode<K, V> rt, K key) {
        try {
            if (key == null)
                throw new Exception("key is null");
            if (rt == null)
                return null;
            if (key.compareTo(rt.getKey()) < 0)
                return search(rt.getLeft(), key);//小于当前key值则往左子树查找
            if (key.compareTo(rt.getKey()) > 0)
                return search(rt.getRight(), key);//大于当前key值则往右子树查找
            return rt.getValue();//找到值
        } catch (Exception e) {
            e.printStackTrace();
            return null;
        }
    }

    public boolean update(K key, V value) {
        return update(root, key, value);
    }

    public boolean update(BinNode<K, V> rt, K key, V value) {
        try {
            if (key == null)
                throw new Exception("Key is null, update failure.");
            if (value == null)
                throw new Exception("value is null, update failure");
            if (key.compareTo(rt.getKey()) == 0) {
                rt.setValue(value);
                return true;
            }
            if (key.compareTo(rt.getKey()) < 0)
                return update(rt.getLeft(), key, value);
            if (key.compareTo(rt.getKey()) > 0)
                return update(rt.getRight(), key, value);
            return false;
        } catch (Exception e) {
            e.printStackTrace();
            return false;
        }
    }

    public boolean isEmpty() {
        return root == null;
    }

    public void clear() {
        root = null;
    }
    
    public int getHeight(BinNode<K, V> rt) {
        int height = 0;
        if (rt == null)
            return 0;
        else
            height++;
        height += Math.max(getHeight(rt.getLeft()), getHeight(rt.getRight()));
        return height;
    }
}

堆

在优先队列的实现中，可以考虑使用 BST，其平均操作的时间代价为 O ( n log ⁡ n ) O(n \log n) O(nlogn)，但是在某些情况下，BST 会变得十分不平衡，使其的性能变得很差，因此发明了一种新的数据结构以保证较高的效率------堆。

定义：堆是一种基于数组实现的完全二叉树。
大顶堆性质 ：任意节点的值 ≥ \ge ≥ 其子节点的值。
- 这意味着堆顶（数组下标 0）总是存储着整个集合中的最大值。
用途：高效地查找和移除最大元素（优先队列），用于堆排序等。

数组表示法 (Array Representation)

父节点 (Parent) : (pos - 1) / 2
左孩子 (Left Child) : 2 * pos + 1
右孩子 (Right Child) : 2 * pos + 2
叶子节点判断 : 利用完全二叉树的性质，如果 pos >= n/2，则该节点必为叶子，无子节点。

纯文本示意（大根堆）：

text 复制代码

       [90]             数组索引:  0   1   2   3   4   5
      /    \            数组内容: [90, 80, 70, 60, 40, 30]
    [80]   [70]
    /  \    /
  [60][40][30]

java 复制代码

/**
 * Max Heap
 * E 必须实现 Comparable 接口用于比较大小
 */
public class MaxHeap<E extends Comparable<E>> { // 大根堆实现
    private E[] Heap; // 指向堆数组的指针
    private int size;    // 堆的最大容量
    private int n;       // 当前堆中的元素数量

    public MaxHeap(E[] h, int num, int max) { // 构造函数
        Heap = h; 
        n = num; 
        size = max; 
        buildheap(); 
    }

    public int heapsize() { // 返回堆的当前大小
        return n; 
    }

    public boolean isLeaf(int pos) { // 若pos是叶子节点位置则返回true
        return (pos >= n/2) && (pos < n); 
    }

    // 返回pos的左孩子的位置
    public int leftchild(int pos) {
        if (pos >= n/2) throw new IllegalArgumentException("Position has no left child");
        return 2 * pos + 1;
    }

    // 返回pos的右孩子的位置
    public int rightchild(int pos) {
        if (pos >= (n - 1)/2) throw new IllegalArgumentException("Position has no right child");
        return 2 * pos + 2;
    }

    public int parent(int pos) { // 返回父节点的位置
        if (pos <= 0) throw new IllegalArgumentException("Position has no parent");
        return (pos - 1)/2;
    }

    public void buildheap() { // 堆化Heap数组的内容
        for (int i = n/2 - 1; i >= 0; i--)  // 非叶子结点下沉
            siftdown(i); 
    }

    private void siftdown(int pos) { // 将元素放到正确的位置
        if (pos < 0 || pos >= n) throw new IllegalArgumentException("Illegal heap position");
        
        while (!isLeaf(pos)) {
            int j = leftchild(pos);
            // 如果有右孩子（右孩子没出界），且右孩子 > 左孩子
            if ((j < (n - 1)) && (Heap[j].compareTo(Heap[j + 1]) < 0))
                j++; // j现在是值较大的孩子的索引
            // 用较大的孩子和pos比 孩子比pos大的话 就交换
            if (Heap[pos].compareTo(Heap[j]) >= 0) return; // 完成（满足大顶堆条件）
            
            swap(pos, j); // 使用内部swap
            pos = j; // 向下移动
        }
    }

    public void insert(E val) { // 将值插入堆
        if (n >= size) throw new RuntimeException("Heap is full");
        
        int curr = n++;
        Heap[curr] = val; // 从堆的末尾开始
        
        // 向上调整，直到当前节点的父节点键大于当前节点键
        while ((curr != 0) && (Heap[curr].compareTo(Heap[parent(curr)]) > 0)) {
            swap(curr, parent(curr)); // 使用内部swap
            curr = parent(curr);
        }
    }

    public E removemax() { // 移除最大值
        if (n <= 0) throw new RuntimeException("Removing from empty heap");
        
        swap(0, --n); // 将最大值与最后一个元素交换
        if (n != 0) // 不是最后一个元素
            siftdown(0); // 将新堆顶元素放到正确位置
        
        return Heap[n];
    }

    // 移除指定位置的元素
    public E remove(int pos) {
        if (pos <= 0 || pos >= n) throw new IllegalArgumentException("Illegal heap position");
        
        swap(pos, --n); // 与最后一个元素交换
        if (n != 0) // 不是最后一个元素
            siftdown(pos); // 将该位置的元素放到正确位置
        
        return Heap[n];
    }
    
    // --- 私有辅助方法 ---
    private void swap(int i, int j) {
        E temp = Heap[i];
        Heap[i] = Heap[j];
        Heap[j] = temp;
    }

} // 类MaxHeap

建堆 (Build Heap)
- 代码对应 ：buildheap()
- 逻辑：不要从头遍历！而是从最后一个非叶子节点 （索引 n/2 - 1）开始，倒序遍历到根节点 0。对每个节点调用 siftdown。
- 效率：这种 Floyd 建堆算法的时间复杂度是 O(n)，比一个个插入 O(n log n) 更快。
下沉 (Sift Down)
- 代码对应 ：siftdown(int pos)
- 逻辑：
  1. 判断当前节点 pos 是否有孩子（!isLeaf(pos)）。
  2. 如果有，找到左右孩子中值较大 的那个（索引记为 j）。
  3. 比较当前节点与较大孩子：
    - 若 Heap[pos] >= Heap[j]：满足堆性质，停下。
    - 若 Heap[pos] < Heap[j]：破坏了规则，交换两者，并将 pos 更新为 j，继续循环。
上浮 (Sift Up - 隐式实现)
- 代码对应 ：insert 方法中的 while 循环。
- 逻辑：
  1. 新元素放在数组末尾 n。
  2. 比较当前元素与父节点 parent(curr)。
  3. 若 当前 > 父（大顶堆），则交换，并继续向上走。
  4. 直到到达根节点或满足 当前 <= 父。
移除最大值 (Remove Max)
- 代码对应 ：removemax()
- 逻辑：
  1. Swap：将堆顶（最大值）与数组最后一个有效元素交换。
  2. Shrink ：堆大小 n 减 1（逻辑上删除了最大值）。
  3. Sift Down ：刚才换上来的末尾元素可能很小，破坏了堆顶的大值性质，需要调用 siftdown(0) 把它沉下去。

复杂度分析

操作	时间复杂度	说明
isLeaf / parent / child	O(1)	简单的数学计算
insert (插入)	O(log n)	最坏情况是从底部上浮到根（树高）
removemax (移除堆顶)	O(log n)	最坏情况是从根下沉到底部（树高）
buildheap (建堆)	O(n)	经过数学级数求和证明，非常高效
空间复杂度	O(n)	依赖外部传入的数组

与标准库 PriorityQueue 的区别

方向不同 ：Java 的 PriorityQueue 默认是小根堆 （Min Heap），而这份代码实现的是大根堆（Max Heap）。
底层操作 ：这份代码暴露了更底层的操作（如 buildheap），并且存储结构是固定大小的数组（依赖传入的 size），不支持自动扩容，而 PriorityQueue 支持动态扩容。

4.5 树和森林采用的各种存储方式的差异性

树的ADT

java 复制代码

interface GINode {  // 通用树节点ADT（抽象数据类型）
    public Object value();  // 返回节点的值
    public boolean isLeaf();  // 若该节点是叶节点，则返回TRUE
    public GINode parent();  // 返回父节点
    public GINode leftmost_child();  // 返回最左子节点
    public GINode right_sibling();  // 返回右兄弟节点
    public void setValue(Object value);  // 设置节点的值
    public void setParent(GINode par);  // 设置父节点
    public void insert_first(GINode n);  // 添加新的最左子节点
    public void insert_next(GINode n);  // 插入新的右兄弟节点
    public void remove_first();  // 移除最左子节点
    public void remove_next();  // 移除右兄弟节点
} // interface GINode


interface GenTree {  // 通用树ADT（抽象数据类型）
    public void clear();  // 清空树
    public GINode root();  // 返回根节点
    // 为树创建新根节点，该根的子节点为first、兄弟节点为sib
    public void newroot(Object value, GINode first, GINode sib);
} // interface GenTree

树和森林的存储方式主要有以下几种，每种方式都有不同的特点和应用场景：

1. 双亲表示法（父指针表示法）

存储结构：使用数组存储结点，每个结点包含数据域和父结点索引
实现方式：

java 复制代码

class ParentNode {
    int data;
    int parentIndex;  // -1表示根结点
}

class ParentTree {
    ParentNode[] nodes;
    int size;
}

特点：
- 查找父结点方便，时间复杂度O(1)
- 查找孩子结点需要遍历整个数组
- 适合查找祖先路径、并查集等应用

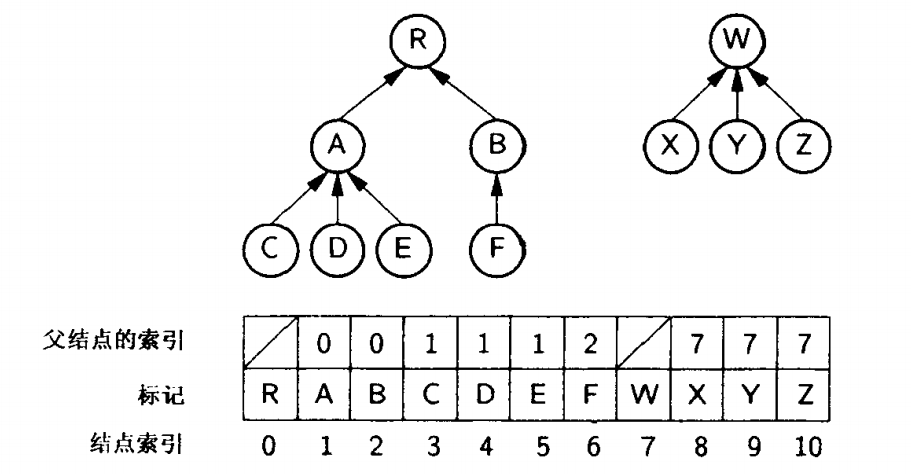
2. 孩子表示法（子节点表表示法）

存储结构：使用数组存储结点信息，同时每个结点维护一个孩子链表
实现方式：

java 复制代码

class ChildNode {
    int childIndex;
    ChildNode next;
}

class TreeNode {
    int data;
    ChildNode firstChild;  // 指向第一个孩子
}

class Tree {
    TreeNode[] nodes;
    int size;
}

特点：
- 查找孩子结点方便
- 查找父结点困难
- 适合需要频繁访问子结点的场景

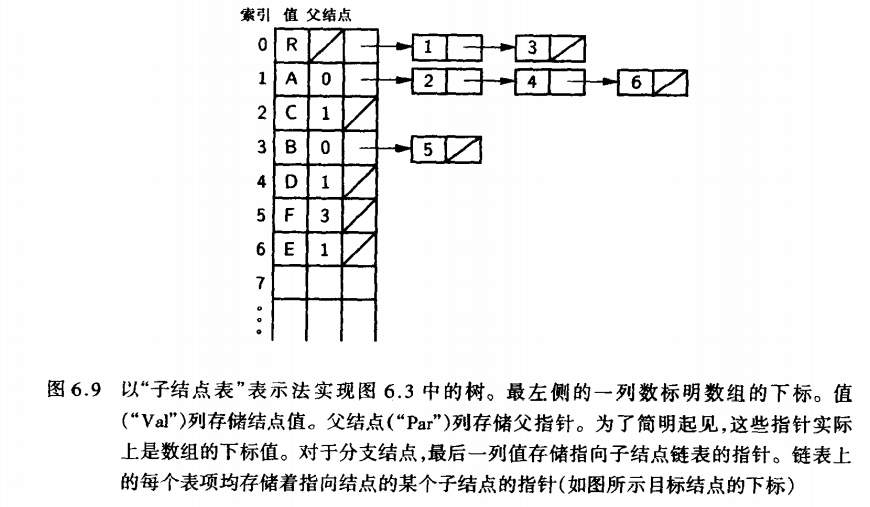
java 复制代码

class MultiChildNode {
    int data;
    int degree;        // 结点的度
    MultiChildNode[] children;  // 孩子指针数组
}

特点：
- 直观反映树的结构
- 适用于度数固定的特殊树

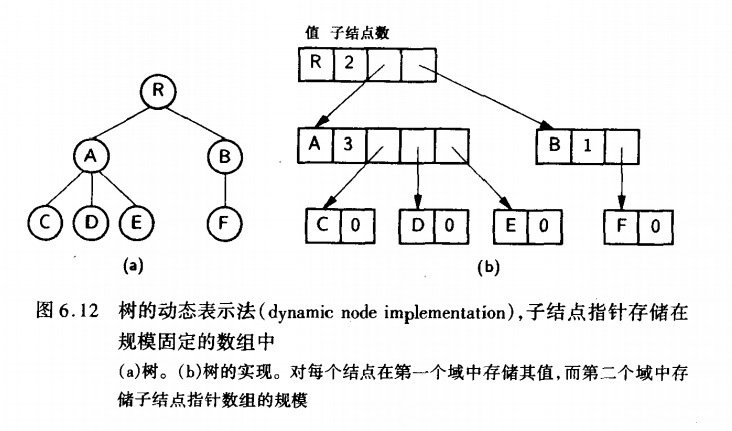
java 复制代码

class AdjTreeNode {
    int data;
    List<AdjTreeNode> children;  // 使用链表或数组存储孩子
}

特点：
- 动态性好，易于添加删除
- 适用于度数不确定的树

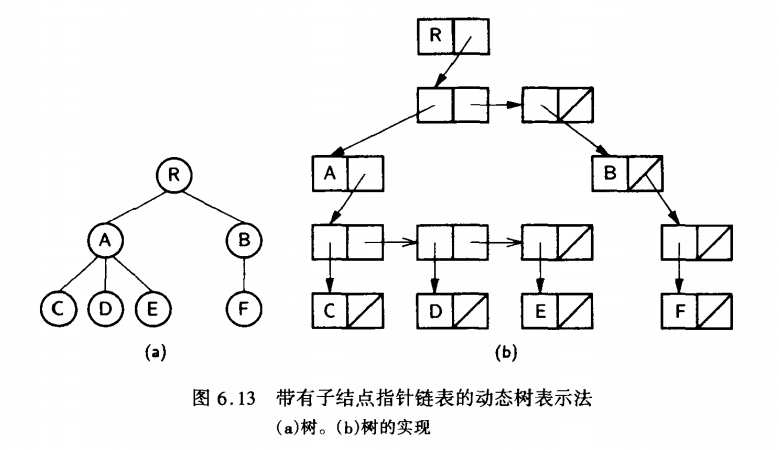
3. 孩子兄弟表示法（左子结点/右兄弟结点表示法）

存储结构：每个结点包含数据、指向第一个孩子的指针、指向右兄弟的指针
实现方式：

java 复制代码

class CSNode {
    int data;
    CSNode firstChild;  // 指向第一个孩子
    CSNode nextSibling; // 指向右兄弟
}

特点：
- 将树转换为二叉树的一种方法
- 实现简单，操作方便
- 广泛应用于树的存储和操作

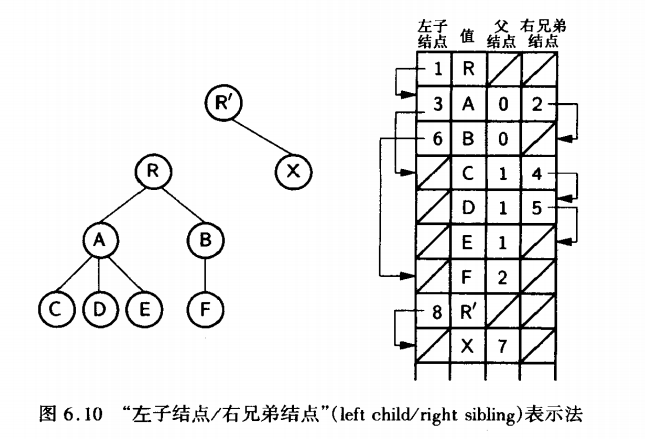
4.6 树和森林与二叉树的转换

（书上似乎只有二叉树与树的转化即左孩子右兄弟法）

1. 树转换为二叉树（左孩子右兄弟法）

转换规则 ：
1. 加线：在所有兄弟结点之间加一条连线。
2. 去线：对每个结点，只保留它与第一个孩子的连线，断开与其他孩子的连线。
示意图：

【原始普通树】【中间步骤】【转换后的二叉树】
A A A
/ | \ / /
B C D B-->C-->D B
/ \ / /
E F E-->F E C
\
F D

中间步骤说明（图中横箭头表示 nextSibling 指针，竖线表示 children 列表）：
- 在原树中每一组同父节点的孩子之间，增加 nextSibling 指针：
  - B.nextSibling -> C, C.nextSibling -> D
  - E.nextSibling -> F
- 同时保留 children 结构（用于之后把第一个孩子作为 left 指针）。
- 最终转换时：
  - 节点的第一个孩子（children.get(0)）会对应为 left（左孩子）。
  - 节点的 nextSibling 会对应为 right（右孩子）。

Java 代码实现：

java 复制代码

// 定义普通树节点
class TreeNode {
    int val;
    List<TreeNode> children = new ArrayList<>();
    TreeNode(int val) { this.val = val; }
}

// 定义二叉树节点
class BinaryTreeNode {
    int val;
    BinaryTreeNode left;  // 指向原树的第一个孩子
    BinaryTreeNode right; // 指向原树的下一个兄弟
    BinaryTreeNode(int val) { this.val = val; }
}

// 转换函数
public BinaryTreeNode treeToBinary(TreeNode root) {
    if (root == null) return null;
    
    // 1. 创建当前的二叉树节点
    BinaryTreeNode newRoot = new BinaryTreeNode(root.val);
    
    // 2. 处理孩子节点
    if (!root.children.isEmpty()) {
        // 原树的第一个孩子 -> 二叉树的左孩子
        newRoot.left = treeToBinary(root.children.get(0));
        
        // 原树的剩余孩子 -> 二叉树左孩子的右链（兄弟链）
        BinaryTreeNode curr = newRoot.left;
        for (int i = 1; i < root.children.size(); i++) {
            curr.right = treeToBinary(root.children.get(i));
            curr = curr.right;
        }
    }
    return newRoot;
}

解释：
- 转换后的二叉树，根节点一定没有右子树（因为根节点在原树中没有兄弟）。
- 原树中的"兄弟关系"在二叉树中变成了"父子关系"（右孩子）。

2. 二叉树转换为树（逆用左孩子右兄弟法）

转换规则（逆转换）：
1. 左孩子 ：二叉树中某结点的左孩子，代表该结点在原树中的第一个孩子。
2. 右孩子 ：二叉树中某结点的右孩子，代表该结点在原树中的兄弟。
- 简单来说：将左孩子和该左孩子右链上的所有节点，都变成当前节点的子节点，而右孩子全部变成兄弟。
示意图：

【二叉树结构】【还原后的普通树】
A A
/ / |
B (B是A的长子) B C D
/ \ (C是B的兄弟) /
E C (D是C的兄弟) E
\ (E是B的长子)
D

Java 代码实现：

java 复制代码

public TreeNode binaryToTree(BinaryTreeNode binaryRoot) {
    if (binaryRoot == null) return null;
    
    TreeNode root = new TreeNode(binaryRoot.val);
    
    // 如果有左孩子，说明原树有子节点
    if (binaryRoot.left != null) {
        // 左孩子是第一个子节点
        root.children.add(binaryToTree(binaryRoot.left));
        
        // 沿左孩子的右链遍历，找回所有兄弟作为子节点
        BinaryTreeNode sibling = binaryRoot.left.right;
        while (sibling != null) {
            root.children.add(binaryToTree(sibling));
            sibling = sibling.right;
        }
    }
    return root;
}

解释：
- 这是一个还原过程。代码中，我们只查看binaryRoot.left，因为binaryRoot.right表示的是root自己的兄弟，不属于root的子树范围（通常根节点右侧为空）。
- 通过遍历左节点的right链，找回了原树中所有的并列兄弟。

3. 森林转换为二叉树

转换规则：
1. 先把森林中的每一棵树各自转换为二叉树。
2. 将第二棵二叉树的根节点，作为第一棵二叉树根节点的右孩子；第三棵作为第二棵的右孩子，依此类推。
- 实质：将森林看作一棵虚拟根节点被移除的树，各树根互为兄弟。
示意图：
复制代码
```
【原始森林】             【树转为二叉树】        【合并后的二叉树】
```
树1: 树2: 树1: 树2: A
A X A X /
/ \ / / / B X <-- X接在A的右边
B C Y B Y / /
/ C Y
C
图解说明：
1. 树1内部：B是A的长子(left)，C是B的兄弟(right) -> A-L->B-R->C
2. 树间关系：X视为A的兄弟(right) -> A-R->X
3. 树2内部：Y是X的长子(left) -> X-L->Y
[原始森林] [每棵树各自转换为二叉树] [最终合并后的二叉树]
树1 树2 树3 二叉树1 二叉树2 二叉树3 （合并结果）
A X M A X M A --->1 root
/ \ / \ /|\ / / / /
B C Y Z P Q R B Y P B X --->2 root
/ / \ \ \ / \ /
E E C Z Q E C Y M --->3 root
\ \ /
R Z P

Q

R

Java 代码实现：

java 复制代码

// 输入是多棵普通树的列表
public BinaryTreeNode forestToBinary(List<TreeNode> forest) {
    if (forest == null || forest.isEmpty()) return null;
    
    // 1. 将第一棵树转为二叉树，作为整体的根
    BinaryTreeNode root = treeToBinary(forest.get(0));
    
    // 2. 后续的树依次挂在右链上
    BinaryTreeNode current = root;
    for (int i = 1; i < forest.size(); i++) {
        current.right = treeToBinary(forest.get(i));
        current = current.right;
    }
    
    return root;
}

解释：
- 森林转二叉树后，根节点可能有右子树，这个右子树就是森林中第二棵树转换来的。
- current.right 的连接操作体现了森林中各树根节点之间的"兄弟"关系。

4. 二叉树转换为森林

转换规则：
1. 若二叉树根节点有右链，则断开右链。
2. 根节点及其左子树（及其左子树的右链）还原为第一棵树。
3. 断下的右链部分（右孩子）作为下一棵树的二叉树形态，重复步骤1、2。
示意图：

【二叉树】【还原出的森林】
A 树1: 树2:
/ \ A X
B X <-- 在这里断开! / /
/ / B Y
C Y /
C

操作步骤：
1. 识别出 A 的右孩子是 X。
2. 切断 A -> X 的连接。
3. 得到两棵二叉树：(A及其左子树) 和 (X及其子树)。
4. 分别调用 binaryToTree 进行还原。

Java 代码实现：

java 复制代码

public List<TreeNode> binaryToForest(BinaryTreeNode binaryRoot) {
    List<TreeNode> forest = new ArrayList<>();
    
    BinaryTreeNode current = binaryRoot;
    while (current != null) {
        // 1. 暂存右子树（这是下一棵树的根）
        BinaryTreeNode nextTreeRoot = current.right;
        
        // 2. 断开右指针，以便将当前节点作为一棵独立的树还原
        // 注意：我们需要先断开，再调用 binaryToTree，否则 binaryToTree 会把右链误判为当前树的兄弟
        current.right = null; 
        
        // 3. 还原当前这棵树并加入森林
        forest.add(binaryToTree(current));
        
        // 4. 恢复右指针(如果需要保持原二叉树结构) 或 直接移动到下一棵
        // 这里我们直接处理下一个
        current = nextTreeRoot;
    }
    
    return forest;
}

解释：
- 此方法通过不断剥离二叉树根节点的右孩子，将其分解为多棵独立的二叉树。
- 然后复用之前的 binaryToTree 方法，将每一棵独立的二叉树还原为普通树。
- 关键点 ：在调用 binaryToTree 之前，必须将 current.right 设为 null，否则还原算法会把后续的树根误认为是当前树根的子节点（兄弟关系）。

4.7 树和森林在遍历方面与二叉树的差异及相关性

1. 树的遍历方式

先根遍历：

访问根结点
从左到右依次先根遍历每棵子树

java 复制代码

void preOrderTraverse(TreeNode root) {
    if (root == null) return;
    visit(root);
    for (TreeNode child : root.children) {
        preOrderTraverse(child);
    }
}

后根遍历：

从左到右依次后根遍历每棵子树
访问根结点

java 复制代码

void postOrderTraverse(TreeNode root) {
    if (root == null) return;
    for (TreeNode child : root.children) {
        postOrderTraverse(child);
    }
    visit(root);
}

层次遍历：（书上没有）

从上到下按层访问
每层从左到右访问

java 复制代码

void levelOrderTraverse(TreeNode root) {
    if (root == null) return;
    Queue<TreeNode> queue = new LinkedList<>();
    queue.offer(root);
    
    while (!queue.isEmpty()) {
        TreeNode node = queue.poll();
        visit(node);
        for (TreeNode child : node.children) {
            queue.offer(child);
        }
    }
}

2. 森林的遍历方式

先序遍历森林：
1. 访问第一棵树的根结点
2. 先序遍历第一棵树的子树森林
3. 先序遍历剩余树构成的森林
java 复制代码
```
void preOrderForest(List<TreeNode> forest) {
    for (TreeNode tree : forest) {
        preOrderTraverse(tree);
    }
}
```
后根遍历森林：
1. 后根遍历第一棵树的子树森林
2. 访问第一棵树的根结点
3. 后根遍历剩余树构成的森林

3. 树、森林与二叉树遍历的对应关系

树/森林遍历	对应二叉树遍历	说明
树的先根遍历	二叉树的先序遍历	树转换为二叉树后，遍历顺序一致
树的后根遍历	二叉树的中序遍历	树转换为二叉树后，遍历顺序一致
森林的先序遍历	二叉树的先序遍历	森林转换为二叉树后，遍历顺序一致
森林的后根遍历	二叉树的中序遍历	森林转换为二叉树后，遍历顺序一致

4. 遍历的相关性证明

树先根遍历 ≡ 二叉树先序遍历：

复制代码

【原始普通树】           【中间步骤】          【转换后的二叉树】
      A                       A                    A
    / | \                   /                     /
   B  C  D                B-->C-->D              B
  / \                    /                     / \
 E   F                  E-->F                 E   C
                                               \   \
                                                F   D

顺序：A -> B -> E -> F -> C -> D

树后根遍历 ≡ 二叉树中序遍历 ：

同上树结构，顺序：E -> F -> B -> C -> D -> A

4.8 并查集的意义其两个基本操作的实现以及重量权衡平衡原则和路径压缩

4.8.1 并查集的意义

"朋友的朋友就是朋友"

并查集主要用于处理不相交集合（Disjoint Sets）的合并及查询问题。它的核心意义在于高效地维护一个动态的集合系统。

应用场景：
- 连通性判断：判断图中的两个点是否连通（例如：两台电脑是否在同一个局域网）。
- 最小生成树：Kruskal 算法的核心组件。
- 亲戚关系/社交网络：判断两个人是否属于同一个家族或朋友圈。
形象理解：
- 这是一个"帮派"管理系统。每个人都有一个老大，如果两个人的老大是同一个人，那他们就是同一个帮派的。
- 如果两个帮派要合并，只需要让其中一个帮派的老大成为另一个帮派老大的小弟即可。

4.8.2 两个基本操作

并查集内部通常用一个数组 parent[] 来实现，parent[i] 表示元素 i 的父节点。

查找 (Find)
功能：找到元素 x 所属集合的代表元素（即"帮派的老大"）。
规则：如果一个节点的父节点是它自己（parent[x] == x），那它就是根节点（老大）。否则，递归向上查找。

java 复制代码

// 基础查找代码
int find(int x) {
    if (parent[x] == x)return x; // 找到了老大
    else return find(parent[x]); // 接着往上找
}

合并 (Union)
功能：将两个元素 x 和 y 所在的集合合并。
步骤：
1. 找到 x 的老大 rootX。
2. 找到 y 的老大 rootY。
3. 如果 rootX 不等于 rootY，就让其中一个指向另一个（例如 parent[rootX] = rootY）。

java 复制代码

// 基础合并代码
void union(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    if (rootX != rootY) {
        parent[rootX] = rootY; // 让X的老大认Y的老大做大哥
    }
}

4.8.3 优化策略一：重量权衡平衡原则 (Weighted Union / Union by Rank)

问题：如果暴力合并，可能会让树退化成一条长链（如下图左），导致查找效率变为 O(N)。
解决：小树挂在大树下。合并时，总是把节点少（或深度小）的树挂在节点多（或深度大）的树下面，这样树的高度增加得最慢。

plaintext 复制代码

【糟糕的合并：把大树挂在小树下】           【平衡合并：把小树挂在大树下】
       3 (小树)                                 1 (大树根)
      /                                       /   \
     1 (大树根)        查询4的路径变长了        2     3 (原来的小树)
    /                                         \
   2                                           4
    \
     4

结果：树越来越高，查询慢                   结果：树高变化小，查询快

实现代码（按重量/大小）

我们需要一个额外的数组 size[] 来记录每棵树的节点数量。

java 复制代码

// 初始化时，每个集合size都是1
int[] size; 

void union(int x, int y) {
    int rootX = find(x);
    int rootY = find(y);
    
    if (rootX == rootY) return;
    
    // 谁大谁做主（小树挂大树）
    if (size[rootX] > size[rootY]) {
        parent[rootY] = rootX;
        size[rootX] += size[rootY]; // 大树吃掉小树，体积增加
    } else {
        parent[rootX] = rootY;
        size[rootY] += size[rootX];
    }
}

4.8.4 优化策略二：路径压缩 (Path Compression)

这是并查集最核心 的优化。
思路：在查找老大（find）的过程中，既然我经过了这条路径上的所有人，我知道大家的老大都是同一个最终BOSS，不如直接把路径上所有人的父节点都直接指向BOSS。

意义：下一次再查询这些节点时，一步就能找到老大，复杂度近乎 O(1)。

plaintext 复制代码

【没有路径压缩】                 【执行路径压缩后】
       1 (老大)                        1 (老大)
      /                             /  |  \
     2                             2   3   4
    /                             
   3                              (2, 3, 4 全都直接连向 1)
  /                               
 4 (查询我)                        

查找4时，递归经过3,2,1。
顺手把4,3,2的父节点全改成1。

实现代码（递归版）

java 复制代码

int find(int x) {
    if (parent[x] == x) return x;
    else return parent[x]= find(parent[x]); // 递归找到老大，并直接赋值给 parent[x]
}

4.8.5 完整代码实现（Java版）

包含路径压缩和按秩合并（Rank，类似高度）的最终版本。

java 复制代码

class UnionFind {
    private int[] parent;
    private int[] rank; // 记录树的高度（近似）

    public UnionFind(int n) {
        parent = new int[n];
        rank = new int[n];
        for (int i = 0; i < n; i++) {
            parent[i] = i; // 初始时，自己是自己的老大
            rank[i] = 1;   // 初始高度为1
        }
    }

    // 查找 + 路径压缩
    public int find(int x) {
        if (parent[x] != x) {
            // 递归寻找根节点，并将沿途节点的父节点直接指向根
            parent[x] = find(parent[x]);
        }
        return parent[x];
    }

    // 合并 + 按秩合并（平衡原则）
    public void union(int x, int y) {
        int rootX = find(x);
        int rootY = find(y);

        if (rootX != rootY) {
            // 只有根不同才合并
            // 高度低的树挂在高度高的树下
            if (rank[rootX] > rank[rootY]) {
                parent[rootY] = rootX;
            } else if (rank[rootX] < rank[rootY]) {
                parent[rootX] = rootY;
            } else {
                // 高度相同，随便挂，被挂的那个树高度+1
                parent[rootY] = rootX;
                rank[rootX] += 1;
            }
        }
    }
    
    // 判断连通性
    public boolean isConnected(int x, int y) {
        return find(x) == find(y);
    }
}

总结

特性	说明
时间复杂度	经过两个优化（路径压缩+平衡原则）后，操作的平均时间复杂度接近 O(1) (即反阿克曼函数 O ( α ( N ) ) O(\alpha(N)) O(α(N))，增长极慢)。
空间复杂度	O(N)，需要存储 parent 数组。
核心思想	1. 找老大 (Find)：认祖归宗，顺便抄近道 (路径压缩)。 2. 合并 (Union)：拜把子，弱者依附强者 (平衡原则)。

补充：4.9 满二叉树、完全二叉树与二叉树定理

满二叉树：full binary tree 满二叉树的每一个结点，要么是一个恰有两个非空结点的分支结点要么是一个叶子结点。
A B C D E F G

完全二叉树 ：complete binary tree 完全二叉树有严格的要求：从根结点起，每一层从左往右填充。一棵高度为d的完全二叉树除了d-1层（最后一层）以外，每一层都是满的
0 1 2 3 4 7 8 9 10 5 6 11

二叉树基本定理：对任何一棵二叉树T，如果其叶结点数为 n 0 n_0 n0，则双孩子结点数为 n 2 n_2 n2，则有 n 0 = n 2 + 1 n_0 = n_2 + 1 n0=n2+1
证明：二叉树中，只有三种结点: 叶结点 n 0 n_0 n0，单孩子结点 n 1 n_1 n1，双孩子结点 n 2 n_2 n2，设该树的结点总数为 n n n，则有 n = n 0 + n 1 + n 2 n = n_0 + n_1 + n_2 n=n0+n1+n2，也有 n = 0 × n 0 + 1 × n 1 + 2 × n 2 ⏟ 分支数 + 1 n = \underbrace{0 \times n_0 + 1 \times n_1 + 2 \times n_2}_{分支数} + 1 n=分支数 0×n0+1×n1+2×n2+1，结合这两个式子消去 n n n 即可证明.
满二叉树定理：非空满二叉树的叶结点数等于其分支结点数+1
证明：满二叉树无单孩子结点 n 1 = 0 n_1=0 n1=0，其分支结点即为双孩子节点 n 2 n_2 n2，由二叉树基本定理，叶结点数 n 0 n_0 n0 = 分支节点数 n 2 n_2 n2 + 1.
复制代码
```
            A
           /  \
          B    C
         /\    /\
        D  E   F  G
       /\  /\  	  /\ 
      H I J K	  L M
```
叶结点数 7 = 分支节点数 6 + 1
一棵非空二叉树空子树的数目等于其结点数目+1
证明：二叉树有 n n n 个结点，每个节点有两个指针，共有 2 n 2n 2n 个，其中非空指针数即为树的边数 n − 1 n-1 n−1，那么空指针数也就是空子树数目为 2 n − ( n − 1 ) = n + 1 2n-(n-1) = n+1 2n−(n−1)=n+1.
复制代码
```
      A
     / ×
    B
   × \
      C
     × ×
```
空子树4 = 结点数3 + 1
复制代码
```
    A
   / ×
  B
 × ×
```
空子树3 = 结点数2 + 1
高度为k的二叉树最多有 2 k − 1 ( k ≥ 1 ) 2^k - 1 (k \geq1) 2k−1(k≥1) 个结点
证明：当二叉树为满二叉树时结点数最多。第 i i i 层最多有 2 i − 1 2^{i-1} 2i−1 个结点，共 k k k 层，故最多结点数为：
∑ i = 1 k 2 i − 1 = 2 k − 1. \sum_{i=1}^k 2^{i-1} = 2^k - 1. i=1∑k2i−1=2k−1.
具有 n n n 个结点的完全二叉树的高度为 ⌊ l o g 2 n ⌋ + 1 \lfloor log_2 n \rfloor +1 ⌊log2n⌋+1 或 ⌈ l o g 2 ( n + 1 ) ⌉ \lceil log_2(n+1) \rceil ⌈log2(n+1)⌉
证明：设高度为 h h h。由完全二叉树定义，前 h − 1 h-1 h−1 层满（共 2 h − 1 − 1 2^{h-1}-1 2h−1−1 个结点），第 h h h 层至少 1 1 1 个、至多 2 h − 1 2^{h-1} 2h−1 个结点，故：
2 h − 1 ≤ n ≤ 2 h − 1 < 2 h 2^{h-1} \le n \le 2^h - 1 < 2^h 2h−1≤n≤2h−1<2h

取对数得
h − 1 ≤ log ⁡ 2 n < h h-1 \le \log_2 n< h h−1≤log2n<h
log ⁡ 2 n < h ≤ log ⁡ 2 n + 1 \log_2 n < h \le \log_2 n + 1 log2n<h≤log2n+1
h = ⌊ log ⁡ 2 n ⌋ + 1. h = \lfloor \log_2 n \rfloor + 1. h=⌊log2n⌋+1.

同时由 2 h − 1 < n + 1 ≤ 2 h 2^{h-1} < n+1 \le 2^h 2h−1<n+1≤2h 取对数可得：
h − 1 < log ⁡ 2 ( n + 1 ) ≤ h h-1 < \log_2(n+1) \leq h h−1<log2(n+1)≤h
h = ⌈ log ⁡ 2 ( n + 1 ) ⌉ . h = \lceil \log_2 (n+1) \rceil. h=⌈log2(n+1)⌉.

知识点详解（下）

下半部分正在更新中

【数据结构】【xjtuse】面向考纲学习（上）

目录

考纲

题型

数据结构基本概念

算法分析

线性表(含栈和队列)

二叉树､树和森林

图

查找

排序

知识点详解（上）

1. 数据结构基本概念

1.1 数据、数据元素、数据项之间的关系

1.2 数据结构的定义

1.3 数据结构的三要素

1.4 数据类型、抽象数据类型和数据结构之间的关系

2. 算法分析

2.1 衡量算法在资源上的两个方面

2.2 算法的渐进性分析方法 以及运用该方法对算法进行评估

2.3 Ο标记法 以及大Ο标记法的意义

2.4 Ω标记法 以及大Ω标记法的意义

2.5 Θ标记法 以及大Θ标记法的意义

2.6 时空权衡原则

3. 线性表(含栈和队列)

3.1 线性表的逻辑结构与基本操作

3.2 顺序表

3.3 链式存储结构的实现技术 例如单向链表及带头节点的链表

3.4 链表

3.5 实际应用中不同存储结构的选取判断能力

3.6 栈与队列的逻辑结构与基本操作

3.7 顺序栈和队列

3.8 链栈和队列

3.9 顺序存储结构中循环队列的实现具体要求

3.10 递归调用和栈之间的关系

3.11 栈和队列的经典应用

4. 二叉树 树和森林

4.1 二叉树、树和森林的定义及三者之间的异同点

4.2 二叉树的四种遍历以及相关操作

4.3 二叉树采用顺序存储结构和链式存储结构的差异性

链式二叉树的实现

4.4 二叉检索树、Huffman编码树及堆的实现

Huffman编码树

二叉搜索树 BST（Binary Search Tree）

堆

4.5 树和森林采用的各种存储方式的差异性

4.6 树和森林与二叉树的转换

4.7 树和森林在遍历方面与二叉树的差异及相关性

4.8 并查集的意义 其两个基本操作的实现 以及重量权衡平衡原则和路径压缩

4.8.1 并查集的意义

4.8.2 两个基本操作

4.8.3 优化策略一：重量权衡平衡原则 (Weighted Union / Union by Rank)

4.8.4 优化策略二：路径压缩 (Path Compression)

4.8.5 完整代码实现（Java版）

补充：4.9 满二叉树、完全二叉树与二叉树定理

知识点详解（下）

2.2 算法的渐进性分析方法以及运用该方法对算法进行评估

2.3 Ο标记法以及大Ο标记法的意义

2.4 Ω标记法以及大Ω标记法的意义

2.5 Θ标记法以及大Θ标记法的意义

3.3 链式存储结构的实现技术例如单向链表及带头节点的链表

4. 二叉树树和森林

4.8 并查集的意义其两个基本操作的实现以及重量权衡平衡原则和路径压缩