矩阵区间更新TLE?试试二维差分

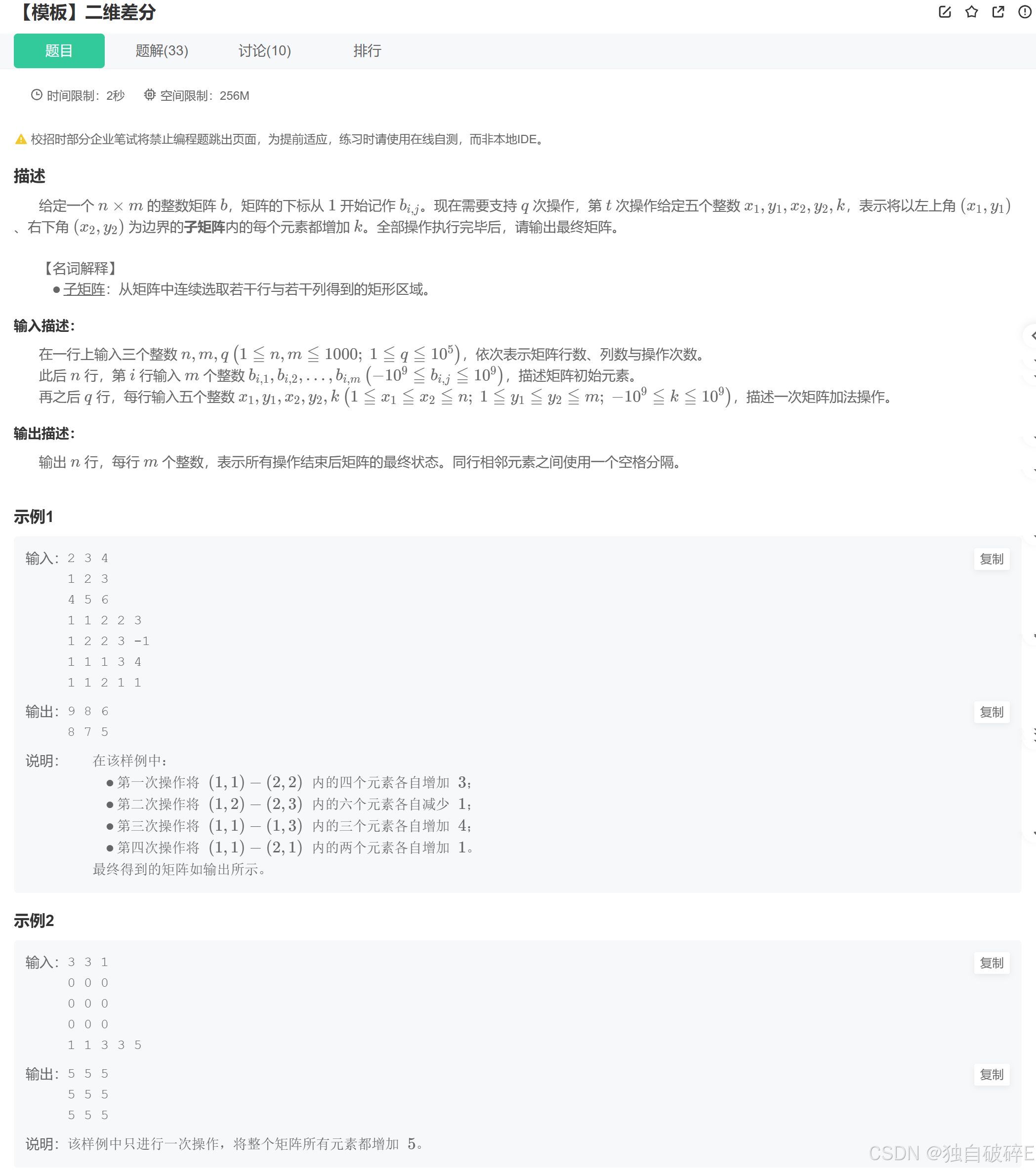
这道题如果用暴力方法，每次更新都要遍历子矩阵内的所有元素，时间复杂度是 O(q×n×m)，数据量大时会超时。

求解思路

在一维数组中，只需要在区间起点加k、终点后一位减k，最后做前缀和就能还原出整个数组。

二维情况下原理相同，只是标记变成了四个角点的操作。

具体来说，要给矩形区域 (a,b) 到 (c,d) 加上 k，在左上角 (a,b) 加k表示从这里开始增加，在右下角外侧的 (c+1,b) 和 (a,d+1) 各减k表示横向和纵向的增加到此为止,最后在 (c+1,d+1) 再加k来抵消多减的部分。

完成所有标记后,通过二维前缀和还原就能得到每个位置的真实值,整个过程每次更新只需要O(1)时间,总体复杂度可以降到O(q + n×m)。

代码实现

java 复制代码

import java.io.*;

public class Main {
    public static int MAXN = 1005;
    public static int MAXM = 1005;
    public static long[][] diff = new long[MAXN][MAXM];
    public static int n, m, q;
    
    // 区间更新：给矩形区域(a,b)到(c,d)加上k
    public static void add(int a, int b, int c, int d, int k) {
        diff[a][b] += k;           // 左上角加k
        diff[c + 1][b] -= k;       // 左下角外减k
        diff[a][d + 1] -= k;       // 右上角外减k
        diff[c + 1][d + 1] += k;   // 右下角外加k
    }
    
    // 通过二维前缀和还原矩阵
    public static void build() {
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                diff[i][j] += diff[i-1][j] + diff[i][j-1] - diff[i-1][j-1];
            }
        }
    }
    
    // 清空差分数组
    public static void clear() {
        for (int i = 1; i <= n + 1; i++) {
            for (int j = 1; j <= m + 1; j++) {
                diff[i][j] = 0;
            }
        }
    }
    
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StreamTokenizer in = new StreamTokenizer(br);
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        
        while (in.nextToken() != StreamTokenizer.TT_EOF) {
            n = (int) in.nval;
            in.nextToken();
            m = (int) in.nval;
            in.nextToken();
            q = (int) in.nval;
            
            // 读入原始矩阵并标记
            for (int i = 1; i <= n; i++) {
                for (int j = 1; j <= m; j++) {
                    in.nextToken();
                    add(i, j, i, j, (int) in.nval);
                }
            }
            
            // 处理q次区间更新操作
            for (int i = 1, a, b, c, d, k; i <= q; i++) {
                in.nextToken();
                a = (int) in.nval;
                in.nextToken();
                b = (int) in.nval;
                in.nextToken();
                c = (int) in.nval;
                in.nextToken();
                d = (int) in.nval;
                in.nextToken();
                k = (int) in.nval;
                add(a, b, c, d, k);
            }
            
            // 还原矩阵
            build();
            
            // 输出结果
            for (int i = 1; i <= n; i++) {
                out.print(diff[i][1]);
                for (int j = 2; j <= m; j++) {
                    out.print(" " + diff[i][j]);
                }
                out.println();
            }
            
            clear();
        }
        
        out.flush();
        out.close();
        br.close();
    }
}

如果觉得有帮助，欢迎点赞、关注、转发~