算法的介绍
类似于数组分块之类的算法题,解决的方法一般为双指针算法 。这里的指针并不是我们所想的指针,不是C语言中所学习的指针,实际上它是利用数组下标来充当指针。设这两个指针为 dest 和 cur ,cur(current) 从左往右扫描数组,遍历数组;dest 根据题目的情况来移动。
算法题目
题目1:283. 移动零 - 力扣(LeetCode)
题目分析:
给定一个数组
nums,编写一个函数将所有0移动到数组的末尾,同时保持非零元素的相对顺序。请注意 ,必须在不复制数组的情况下原地对数组进行操作
题目要求中提到"在不复制数组的情况下原地对数组进行操作"说明不能新建一个数组,将非0元素移至新建数组的前面,将0元素移至新建数组的后面,然后再返回新建数组;"保证非0元素的相对顺序"指的是 0 1 0 3 12 经过修改后变为 1 3 12 0 0。
题目示例:
示例 1:
输入: nums = [0,1,0,3,12] 输出: [1,3,12,0,0]示例 2:
输入: nums = [0] 输出: [0]
算法思路

dest 和 cur 指针有什么作用呢?
dest(destination) 已处理的区间内,非0元素的最后一个位置
cur(current) 从左往右扫描数组,遍历数组
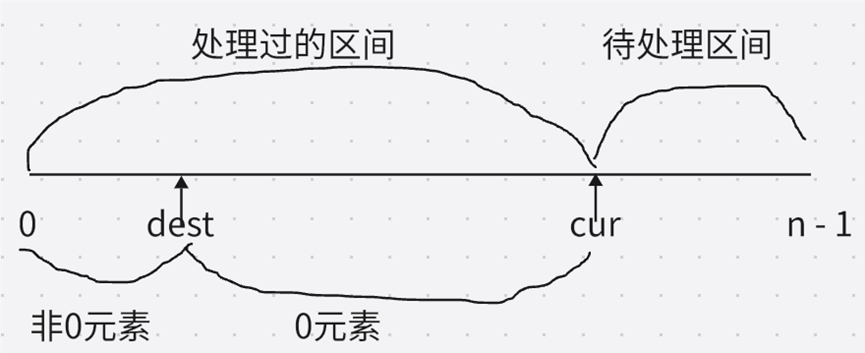
dest 和 cur 指针将数组分成了三个区间:
[ 0, dest ]:已经处理过的区间,元素均为非0元素
[ dest + 1, cur - 1 ]:已经处理过的区间,元素均为0元素
[ cur, n -- 1 ]:待处理区间
当 cur 指针遍历完数组,也就是 cur == n 时,数组就处理完毕了,因为待处理的区间消失了.
具体步骤
cur 从前往后遍历的过程中:
遇到 0 元素:cur++
遇到非0元素,dest++,交换dest 和 cur 指向的元素,交换完毕之后,让 dest 和 cur 分别 ++
这个思想在数据结构的快速排序中也使用过,找一个基准值,基准值的左边都是小于或等于基准值,基准值的右边都是大于基准值。
代码实现(时间复杂度:O(N))
cpp
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int dest = -1;
int cur = 0;
// cur 大于数组的元素个数之后说明修改完毕
while(cur < nums.size())
{
if(nums[cur] != 0)
{
swap(nums[dest + 1], nums[cur]);
dest++;
}
cur++;
}
}
};题目2:1089. 复写零 - 力扣(LeetCode)
题目分析
给你一个长度固定的整数数组
arr,请你将该数组中出现的每个零都复写一遍,并将其余的元素向右平移。注意:请不要在超过该数组长度的位置写入元素。请对输入的数组 就地进行上述修改,不要从函数返回任何东西
"不要在超过该数组长度的位置写入元素"指的是原数组有几个元素,复写0操作之后仍然有几个元素。
题目示例
示例 1:
输入:arr = [1,0,2,3,0,4,5,0] 输出:[1,0,0,2,3,0,0,4] 解释:调用函数后,输入的数组将被修改为:[1,0,0,2,3,0,0,4]示例 2:
输入:arr = [1,2,3] 输出:[1,2,3] 解释:调用函数后,输入的数组将被修改为:[1,2,3]
算法思路
先根据"异地"操作,然后优化成双指针下的"就地"操作。
如果这道题采用从左向右的方法,可能会出现问题,模拟过程:

难道双指针算法不能解决这个问题吗?从左向右不行,试试从后向前。
让 dest 指向数组的最后一个元素,cur 指向最后一个复写的元素,模拟过程:

思路:
先找到最后一个复写的数,怎么找最后一个复写的数呢?使用双指针算法,使用左右指针dest 指向 -1 位置,cur 指向 0 位置
先判断 cur 位置的值,决定dest向后移动一步还是两步,判断 dest 是否已经到结束位置,cur++
操作演示:
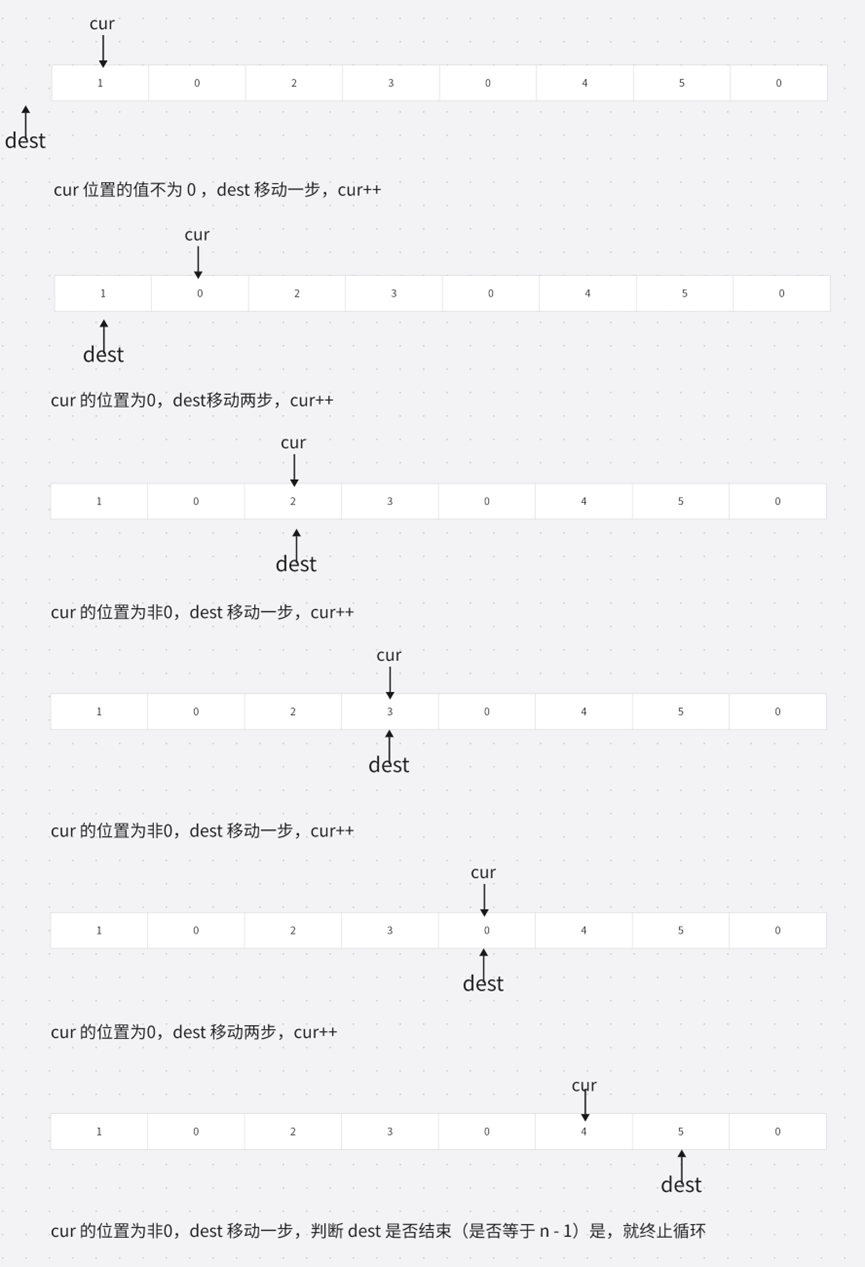
最终 cur 指向的数就是最后一个复写的数。
但是存在特例:
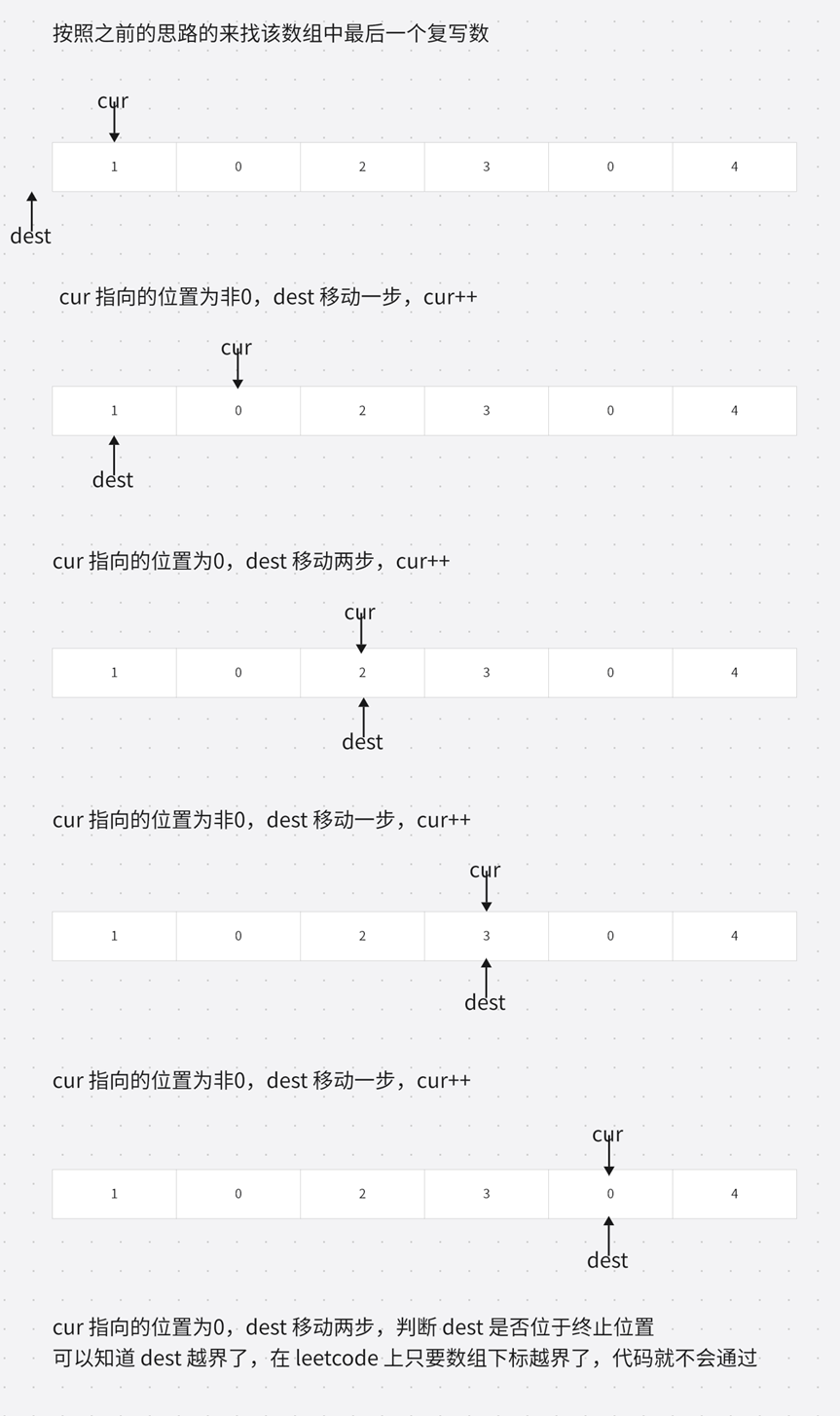
所以需要在原来的不步骤中的第一步后再加一步 ------ 处理边界情况。什么情况下 dest 会越界呢?当 cur 指向的位置为0时。
处理步骤:将 n -- 1位置的值修改为0,再让 dest 先前移动两步,cur 向前移动一步,之后便正常执行复写操作。
最终思路:
cur 找0,dest 复写
当 cur 指向的位置为非0,dest复写值,cur--,dest--
当cur指向的位置为0,dest复写两遍0,cur - - ,dest--
- 当 cur 小于 0,复写完毕
代码实现(时间复杂度O(N))
cpp
class Solution {
public:
void duplicateZeros(vector<int>& arr) {
int dest = -1;
int cur = 0;
int n = arr.size();
// 先找到最后一个复写的数
while(cur < n)
{
if(arr[cur] != 0){ dest++; }
else{ dest += 2; }
if(dest >= n - 1){ break; }
cur++;
}
// 边界处理
if(dest == n)
{
arr[n - 1] = 0;
if(dest )
dest -= 2;
cur--;
}
// 从后向前执行复写操作
while(cur >= 0)
{
if(arr[cur] != 0)
{
arr[dest--] = arr[cur--];
}
else
{
arr[dest--] = 0;
arr[dest--] = 0;
cur--;
}
}
}
};题目3:202. 快乐数 - 力扣(LeetCode)
题目分析
编写一个算法来判断一个数
n是不是快乐数。「快乐数」 定义为:
- 对于一个正整数,每一次将该数替换为它每个位置上的数字的平方和。
- 然后重复这个过程直到这个数变为 1,也可能是 无限循环 但始终变不到 1。
- 如果这个过程 结果为 1,那么这个数就是快乐数。
如果
n是 快乐数 就返回true;不是,则返回false。
这种定义题,尤其要读懂它的定义。
题目示例
示例 1:
输入:n = 19 输出:true 解释: 12 + 92 = 82 82 + 22 = 68 62 + 82 = 100 12 + 02 + 02 = 1示例 2:
输入:n = 2 输出:false
示例解析
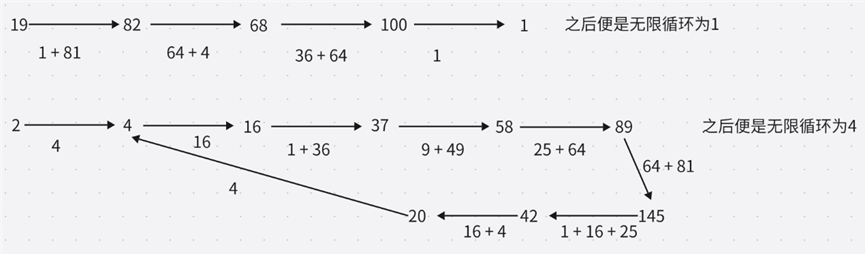
任何一个数,在经历本题操作之后,都会循环,只是一种循环中环内的数均为1,一种循环中换内的数均不为1。一个数串一个数,就像链表一样。在之前学习数据结构链接时,曾提到如何判断链表有环?使用快慢指针算法。所以题目的问题就简化成了,判断环内的元素是否为1,为1即为快乐数,不为1就不是快乐数。
算法思路
定义快慢指针,慢指针指向第一个数,快指针指向第二个数
慢指针每次向后移动一步,快指针每次移动两步
判断相遇时的值
代码实现(时间复杂度O(logn))
cpp
class Solution {
public:
// 计算每个位置上的数字的平方和
int TotalSs(int n)
{
int ret = 0;
while(n)
{
int num = n % 10;
ret += num * num;
n /= 10;
}
return ret;
}
bool isHappy(int n) {
// 定义快慢指针 --- 让快慢指针的初始至不同
int slow = n;
int fast = TotalSs(n);
// 只要快慢指针相遇就跳出循环
while(slow != fast)
{
// 慢指针走一步
slow = TotalSs(slow);
// 快指针走两步
fast = TotalSs(TotalSs(fast));
}
return slow == 1;
}
};为什么一直变化下去,一定会成环?不可能一直变化下去,一直不成环吗?一定不可能。
解释
鸽巢原理(抽屉原理):有 n 个巢,有n + 1 个鸽子,得出结论:至少有一个巢穴中的鸽子数量大于1。
取大数来讲解:判断 999999999 是否是快乐数,每个数平方和为 810,每位数都是个位数的最大值9,所以810一定是9999999999变化过程中最大的数,也就是说之后变化的数都位于 [1,810] 这个区间内,假设经过810次变化之后都没有出现重复的数,那么经过一次变化之后,一定会出现重复的数,这就说明了,一个数一直变化下去,一定会成环。
题目4:11. 盛最多水的容器 - 力扣(LeetCode)
题目分析
给定一个长度为
n的整数数组height。有n条垂线,第i条线的两个端点是(i, 0)和(i, height[i])。找出其中的两条线,使得它们与
x轴共同构成的容器可以容纳最多的水。返回容器可以储存的最大水量。
**说明:**你不能倾斜容器。
题目示例
示例 1:
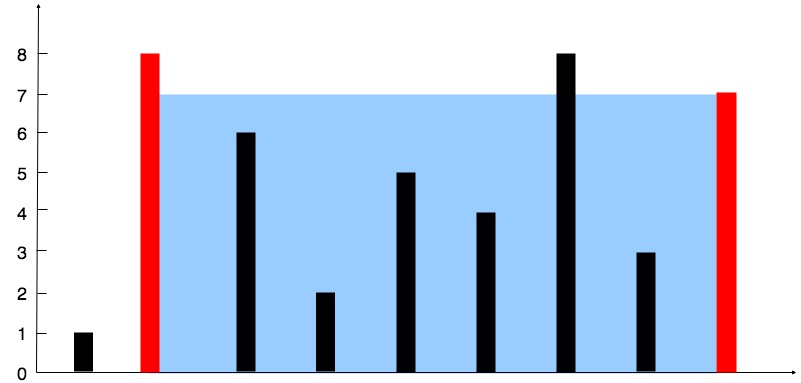
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。示例 2:
输入:height = [1,1] 输出:1
算法原理
思路1:暴力解法
选取两个线,看哪两个线组成的容器的容积最大。直接暴力枚举出所有的情况,找出里面的最大值。
代码实现
cpp
class Solution {
public:
int maxArea(vector<int>& height) {
// 定义一个最大值
int maxnum = 0;
for(int i = 0; i < height.size(); i++)
{
for(int j = i + 1; j < height.size(); j ++)
{
// 木桶效应
int min = height[i] < height[j] ? height[i] : height[j];
if(min * (j - i) > maxnum)
{
maxnum = min * (j - i);
}
}
}
return maxnum;
}
};可以试试看这个代码是否可以通过,一定不能,因为超时了。时间复杂为:O(N^2)。
思路2:前后指针
从区间 [ 1,8,6,2,5,4,8,3,7 ] 中取一区间 [ 6,2,5,4 ],V = height * wide,取左右的数 6 和 4,height 为 4,wide 为 3,V 为12;接下来拿 4,2 来计算,可以发现 height 在减小,wide 在减小,所以V也在减小;拿 4,5 来计算,可以发现 height 不变,wide 在减小,所以 V 也在减小。以6,4 中最小的数为固定线,向内遍历,得到的结果一定比6,4计算的结果要小。因此在取左右区间时,更新左右两数中最小的数。
具体思路:
定义两个指针left,right 一个指向数组的最左边,一个指向数组的最右边
计算容器的大小,判断哪个容器的容积大谁小谁移动
判断 left 和 right 哪个数小,若 left 的数小,则left++;若right的数小,则 right --
代码实现(时间复杂度O(N))
cpp
class Solution {
public:
int maxArea(vector<int>& height) {
// 定义两个指针
int left = 0;
int right = height.size() - 1;
int maxVolume = 0;
while(left < right)
{
// 取数的最小值
int minNum = min(height[left], height[right]);
// 计算容积大小
int volume = minNum * (right - left);
// 取容积中的最大值
maxVolume = max(volume, maxVolume);
// 前后指针移动
if(height[left] < height[right]){ left++; }
else{ right--; }
}
return maxVolume;
}
};题目5:611. 有效三角形的个数 - 力扣(LeetCode)
题目分析
给定一个包含非负整数的数组
nums,返回其中可以组成三角形三条边的三元组个数。
题目示例
示例 1:
输入: nums = [2,2,3,4] 输出: 3 解释:有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3示例 2:
输入: nums = [4,2,3,4] 输出: 4
算法原理
补充点数学知识
给我们三个数,如何判断是否能够构成三角形? a b c
只需要 a + b > c a + c > b b + c > a,这样需要比较三次,这道题使用这个来判断,不高效
接下来介绍另一种判断方法
若我们知道这三个数的大小顺序,仅需比较一次即可 min + medium > max,这个优化方案,需要先对数组排序
思路1:暴力枚举
暴力枚举所有能组成三角形的三个数,然后再统计个数。先固定第一个数,再固定第二个数,去找第三个数,这样需要三层循环。
代码实现
cpp
class Solution {
public:
bool CmpTn(int i, int j, int k)
{
if((i + j > k) && (i + k > j) && (j + k > i))
{
return true;
}
return false;
}
int triangleNumber(vector<int>& nums) {
// 暴力枚举
int count = 0; // 计数器
for(int i = 0; i < nums.size(); i++)
{
for(int j = i + 1; j < nums.size(); j++)
{
for(int k = j + 1; k < nums.size(); k++)
{
if(CmpTn(nums[i], nums[j], nums[k]))
{
count++;
}
}
}
}
return count;
}
};时间超出限制,时间复杂度为O(3*N^3)。
思路2:利用单调性,使用双指针算法来解决问题
若将数组排序,再去比较统计,只需比较一次,所以时间复杂度为N^3,再加上排序的时间复杂度 nlogn ,结果为 N^3 + nlogn 远远小于 3 * N^3。不仅如此,我们还可以更容易的想到优化方案。利用单调性,使用双指针算法来解决该问题。
分析:
有一串已经排序好了的数组序列:2 2 3 4 5 9 10。
固定最大值 10,定义左右两指针,分别指向2和9,2 + 9 > 10,再来看看[ 2,9 ]区间中的数有什么特点,a+b 都大于 c 了,更何况后面大于 a 的数呢?所以不用再判断2之后的数与9的情况了。再修改最大值,9改为5,2 + 5 < 10,既然 a + b 都小于 c 了,更何况 b 前面小于 b 的数呢?所以修改 a 。一直重复上述的过程。固定10的情况考虑完了,接下来再固定9,以此类推。
具体步骤:
先固定最右边的数
在最大数的左区间内,使用双指针算法
定义left,right指针,若left指向的值加上right指向的值大于固定数,则统计right左边有几个数(right -- left 即可得到),然后right--;若left指向的值加上right指向的值小于固定数,则 left++;直到 left >= right
- 换一个固定的数,更新左右指针
代码实现(时间复杂度O(N^2))
cpp
class Solution {
public:
int triangleNumber(vector<int>& nums) {
// 排序
sort(nums.begin(), nums.end());
// 固定最大值
int max = nums.size() - 1;
// 定义计数器
int count = 0;
while(max >= 2)
{
// 将双指针定义在循环内部,方便实时更新
int left = 0;
int right = max - 1;
while(left < right)
{
if(nums[left] + nums[right] > nums[max])
{
count += right - left; // 计数
right--;
}
else
{
left++;
}
}
// 更换固定数
max--;
}
return count;
}
};题目6:和为S的两个数字_牛客题霸_牛客网
题目分析
输入一个递增排序的数组array和一个数字S,在数组中查找两个数,使得他们的和正好是S,如果有多对数字的和等于S,返回任意一组即可,如果无法找出这样的数字,返回一个空数组即可。
数据范围:
0<=len(array)<=105
1<=array[i]<=106
题目示例
示例1
输入:[1,2,4,7,11,15],15
复制返回值:[4,11]
复制说明:返回[4,11]或者[11,4]都是可以的
示例2
输入:[1,5,11],10
返回值:[]
复制说明:不存在,返回空数组
示例3
输入:[1,2,3,4],5
复制返回值:[1,4]
复制说明:返回[1,4],[4,1],[2,3],[3,2]都是可以的
算法原理
思路1:暴力解法
从第一个数开始,与后面的数相加,若有相加等于目标值 target 的,则返回这两个数。
代码实现:
cpp
class Solution {
public:
vector<int> FindNumbersWithSum(vector<int> array,int sum) {
// 暴力解法
for(int i = 0; i < array.size(); i++)
{
for(int j = i; j < array.size(); j++)
{
if(array[i] + array[j] == sum)
{
return {array[i], array[j]};
}
}
}
return {};
}
};时间复杂度过高,为O(N^2),题目不通过。
思路2:利用函数的单调性,使用双指针算法解决问题
注意到这个数组序列是递增的,那么可以使用双指针算法。
分析:序列:1,2,4,7,11,15 target = 15
定义两个指针 left,right,分别指向数组的开头和结尾,即1 和 15。
两数相加,与 target 相比较,发现比 target 大;既然 1 + 15都比 target 大了,更何况 1 后面的数呢?所以1后面的数就不用与 15 相加,再与 target 相比较了
继续缩小区间 right--,1 和 11,两数相加,与 target 相比较,发现比 target 小;既然1 + 11都比 target 小了,更何况11前面的数呢?所以11前面的数就不需要与1相加,再与target相比较了;继续缩小区间 left++。
以此类推,直到找到相加等于 target 的两数返回两数即可。
具体步骤:
定义两个指针,分别指向序列的开头和结尾
若left + right > target,则 right--
若left + right < target,则 left++;若 left + right == target,则直接返回这两数
- 若找不到,返回空序列
代码实现
cpp
class Solution {
public:
vector<int> FindNumbersWithSum(vector<int> array,int sum) {
// 定义左右两个指针
int left = 0;
int right = array.size() - 1;
// 循环相加
while(left < right)
{
if(array[left] + array[right] > sum){ right--; }
else if(array[left] + array[right] < sum){ left++; }
else{ return {array[left], array[right]}; }
}
return {};
}
};题目7:15. 三数之和 - 力扣(LeetCode)
题目分析
给你一个整数数组
nums,判断是否存在三元组[nums[i], nums[j], nums[k]]满足i != j、i != k且j != k,同时还满足nums[i] + nums[j] + nums[k] == 0。请你返回所有和为0且不重复的三元组。**注意:**答案中不可以包含重复的三元组。
满足"i != j、i != k且j != k"说明这三个数的下标位置不一样。
题目所提到的注意事项到底是什么意思?什么是不重复?看题目示例。
题目示例
示例 1:
输入:nums = [-1,0,1,2,-1,-4] 输出:[[-1,-1,2],[-1,0,1]] 解释: nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。 nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。 nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。 不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。 注意,输出的顺序和三元组的顺序并不重要。示例 2:
输入:nums = [0,1,1] 输出:[] 解释:唯一可能的三元组和不为 0 。示例 3:
输入:nums = [0,0,0] 输出:[[0,0,0]] 解释:唯一可能的三元组和为 0 。
示例1中的序列 [-1,0,1] 与 [0,1,-1] 就是重复的,因此只返回其中一个序列;此外还提到了"输出的顺序和三元组的顺序并不重要",也就是说,对于序列 [-1,0,1] 来说,只要其中的内容是一样的,不管你返回的是 [-1,1,0] 还是其它都可以;先返回 [-1,0,1] 还是 [-1,-1,2] 都可以,顺序不重要。
题目的难点在于如何完成去重操作。
算法原理
思路1:暴力解法
先排序,再暴力枚举,最后利用 set 去重,结果会是超时。
思路2:排序,使用双指针算法
分析:

具体步骤:
排序
固定一个数 min,仅需保证 min <= 0即可
在 min 数的后面区间内,利用双指针算法快速找到两个和与 min 相加等于0的数
注意细节:
- 去重
当找到一种结果之后,left 和 right 指针要跳过重复元素;当使用完双指针算法之后,min 也要跳过重复元素
- 不漏
找到一种结果之后,指针不要停,缩小区间,继续寻找
特殊情况:指针可能会越界,如序列为 [ 0,0,0,0 ]时,指针会越界
代码实现(时间复杂度O(N^2))
cpp
class Solution {
public:
vector<vector<int>> threeSum(vector<int>& nums) {
// 返回值
vector<vector<int>> ret;
// 排序
sort(nums.begin(), nums.end());
// 序列的大小
int n = nums.size();
// 固定基准值 --- ++操作放到循环中取处理,为了进行去重操作
for(int min = 0; min < n; )
{
// 基准值仅需 <= 0 即可
if(nums[min] > 0)
{
break;
}
// 定义两个指针
int left = min + 1;
int right = n - 1;
while(left < right)
{
int sum = nums[left] + nums[right] + nums[min];
if(sum > 0) { right--; }
else if(sum < 0) { left++; }
else
{
ret.push_back({nums[min], nums[left], nums[right]});
// 指针不要停,缩小区间,继续查找
left++;
right--;
//去重 --- left
// left < right 是为了避免 left 越界
while(left < right && nums[left] == nums[left - 1])
{
left++;
}
// 去重 --- right
// left < right 是为了避免 right 越界
while(left < right && nums[right] == nums[right + 1])
{
right--;
}
}
}
// 先让 min++,方便完成去重操作
min++;
// 去重 --- min
// min < n 是为了避免 min 越界
while(min < n && nums[min] == nums[min - 1])
{
min++;
}
}
return ret;
}
};题目8:18. 四数之和 - 力扣(LeetCode)
题目分析
给你一个由
n个整数组成的数组nums,和一个目标值target。请你找出并返回满足下述全部条件且不重复 的四元组[nums[a], nums[b], nums[c], nums[d]](若两个四元组元素一一对应,则认为两个四元组重复):
0 <= a, b, c, d < na、b、c和d互不相同nums[a] + nums[b] + nums[c] + nums[d] == target你可以按 任意顺序 返回答案 。
这里的"不重复"与三数之和的"不重复"是一个意思。
题目示例
示例 1:
输入:nums = [1,0,-1,0,-2,2], target = 0 输出:[[-2,-1,1,2],[-2,0,0,2],[-1,0,0,1]]示例 2:
输入:nums = [2,2,2,2,2], target = 8 输出:[[2,2,2,2]]
算法原理
解法:双指针
先排序,再利用双指针。在三数之和中,先固定一个数,再在后面的区间中,找另外两个数;而在四数之和中,也是先固定一个数,再在后面的区间中,再固定一个数,最后 left 和 right 指向剩余的区间,在该区间中找另外两个数。
具体步骤:
固定一个数 min1
在min1后面的区间内,利用"三数之和"找到三个数,使这三数之和与min1相加,等于target
注意细节:
- 去重
当找到一种结果之后,left 和 right 指针要跳过重复元素;当使用完双指针算法之后,min 也要跳过重复元素
- 不漏
找到一种结果之后,指针不要停,缩小区间,继续寻找
- 避免指针越界
代码实现(时间复杂度O(N^3))
cpp
class Solution {
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
// 排序
sort(nums.begin(), nums.end());
// 返回值
vector<vector<int>> ret;
// 数组的长度
int n = nums.size();
// 定义两个指针
int left = 0;
int right = n - 1;
// 固定第一个基准值
for(int min1 = 0; min1 <= n - 4; )
{
// 固定第二个基准值
for(int min2 = min1 + 1; min2 <= n - 3; )
{
// 定义双指针
int left = min2 + 1;
int right = n - 1;
while(left < right)
{
// 求 min1 min2 left right 位置的和
// nums[i]的取值范围很大,int类型可能不满足范围
long long sum = (long long)nums[min1] + nums[min2] + nums[left] + nums[right];
// sum > target,right向前移动
if(sum > target){ right--; }
// sum < target,left向后移动
else if(sum < target){ left++; }
else
{
ret.push_back({nums[min1], nums[min2], nums[left], nums[right]});
// 指针将继续移动,缩小区间范围
left++;
right--;
// 去重 --- right,left不能越界
while(left < right && nums[right] == nums[right + 1])
{
right--;
}
// 去重 --- left
while(left < right && nums[left] == nums[left - 1])
{
left++;
}
}
}
// 跳出循环后,更改min2基准值
min2++;
// min2 去重
while(min2 <= n - 3 && nums[min2] == nums[min2 - 1])
{
min2++;
}
}
// 跳出循环后,更改min1基准值
min1++;
// min1 去重
while(min1 <= n - 4 && nums[min1] == nums[min1 - 1])
{
min1++;
}
}
return ret;
}
};