文章目录
当你迷茫的时候,请回头看看 目录大纲,也许有你意想不到的收获
前言
入门 AI 不容易,先掌握 机器学习 中的一些理论,再是 深度学习,一堆算法,数学公式,矩阵概率论等理论。我也看了一些机器学习的书籍,可谓是五花八门,什么牛鬼蛇神都有,大多我都不太满意。
专业人写的书 晦涩难懂,理论推导一闪而过,他们会觉得这很易证;业余人写的书 漏洞百出,推导不严谨反而写错,这就给想入门的人雪上加霜。求人不如求己,想了解原理,亲自推算一遍!自己的才是最好的!
一元线性回归
先从我们熟悉的地方开始,这是一条 直线 的函数表达式,我们初中学过:
y = w x + b y=wx+b y=wx+b
函数也是有生活气息的,比如这个 线性函数,y 表示体重,x 表示饭量,那这条直线可以这样说:假如有只小猪重 1 斤(b=1),根据我的观察,它大概吃一碗饭就长一斤肉(w=1)。
那么当它吃完 3 碗饭时(x=3),小猪重 y=x+1=3+1= 4 斤,来做个统计:
| 饭量 x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|---|
| 理论重量 y ^ \hat{y} y^ | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 实际重量 y | 1 | 2.11 | 2.98 | 4.32 | 5.21 | 6.01 | 7.33 | 7.99 | 9.12 | 10.44 |
| 偏差 ∣ y ^ − y ∣ |\hat{y}-y | ∣y^−y∣ | 0 | 0.11 | 0.02 | 0.32 | 0.21 | 0.01 | 0.33 | 0.01 | 0.12 | 0.44 |
理想很丰满,现实很骨感,理论值总是非常完美的,但实际上是 有零有整 的,会出现一些 偏差,这都是正常的,比如今天吃一碗饭不够份量,小猪吃的洒了一些......
偏差
怎么验证理论与实际的符合度呢?也就是小猪成长的重量是否就是 y = x + 1 y=x+1 y=x+1 这个规律呢?会不会是其他的函数呢?
那么这里就引入了 残差平方和 RSS,假如总共有 m 个样本,在第 i 个样本中, y i ^ \hat{y_i} yi^ 为第 i 个样本数据预测值 ( y i ^ = w x i + b \hat{y_i}=wx_i+b yi^=wxi+b), y i y_i yi 为第 i 个样本数据真实值,RSS 计算公式为:
R S S = ∑ i = 1 m ( y i ^ − y i ) 2 RSS=\sum\limits_{i=1}^{m}{(\hat{y_i}-y_i)^2}\\[10pt] RSS=i=1∑m(yi^−yi)2
以上面例子来说,我观察了 10 次,共有 10 个样本(m=10),第 i 个样本观测值可以用 ( x i , y i ) (x_i , y_i) (xi,yi) 表示:
P 1 ( 0 , 1 ) , P 2 ( 1 , 2.11 ) , P 3 ( 2 , 2.98 ) , P 4 ( 3 , 4.32 ) , ... ... , P 10 ( 9 , 10.44 ) P_1(0,1),P_2(1,2.11),P_3(2,2.98),P_4(3,4.32),......,P_{10}(9,10.44) P1(0,1),P2(1,2.11),P3(2,2.98),P4(3,4.32),......,P10(9,10.44)
R S S = ∑ i = 1 m ( y i ^ − y i ) 2 = ∑ i = 1 m ( w x i + b − y i ) 2 RSS=\sum\limits_{i=1}^{m}{(\hat{y_i}-y_i)^2} =\sum\limits_{i=1}^{m}{(wx_i+b-y_i)^2} RSS=i=1∑m(yi^−yi)2=i=1∑m(wxi+b−yi)2
只要找到一条直线,也就是确定w和b的值,令残差平方和 RSS 达到最小,那么就可以说这条直线非常拟合现实情况了。
最小二乘法
求解 RSS 最小 就是 最小二乘法,也就是 最小残差平方和。
这里解释一下:
二乘:二次方,平方,这里也就是残差平方和
我还特意查了一下,京师大学堂(后来的北京大学)数学系的 顾澄 老前辈1910 年翻译的,这就属于世纪互动了!
y i ^ = w x i + b R S S = ∑ i = 1 m ( y i ^ − y i ) 2 \hat{y_i}=wx_i+b \\[10pt] RSS=\sum\limits_{i=1}^{m}{(\hat{y_i}-y_i)^2}\\[10pt] yi^=wxi+bRSS=i=1∑m(yi^−yi)2
为了求导方便少带系数,令:
E = 1 2 R S S = 1 2 ∑ i = 1 m ( y i ^ − y i ) 2 u i = y i ^ − y i = w x i + b − y i E = 1 2 ∑ i = 1 m u i 2 E=\frac{1}{2}{RSS}=\frac{1}{2}\sum\limits_{i=1}^{m}{(\hat{y_i}-y_i)^2}\\[10pt] u_i={\hat{y_i}-y_i}=wx_i+b-y_i\\[10pt] E=\frac{1}{2}\sum\limits_{i=1}^{m}{u_i}^2\\[10pt] E=21RSS=21i=1∑m(yi^−yi)2ui=yi^−yi=wxi+b−yiE=21i=1∑mui2
提前准备一下求导,后面会用到:
∂ E ∂ u i = u i ∂ u i ∂ w = x i ∂ u i ∂ b = 1 \frac{\partial E}{\partial u_i}=u_i \\[10pt] \frac{\partial u_i}{\partial w}=x_i \\[10pt] \frac{\partial u_i}{\partial b}=1 \\[10pt] ∂ui∂E=ui∂w∂ui=xi∂b∂ui=1
对于 w,b 变量来说,当 E 取到最小值时,也就是处于抛物面的谷底:
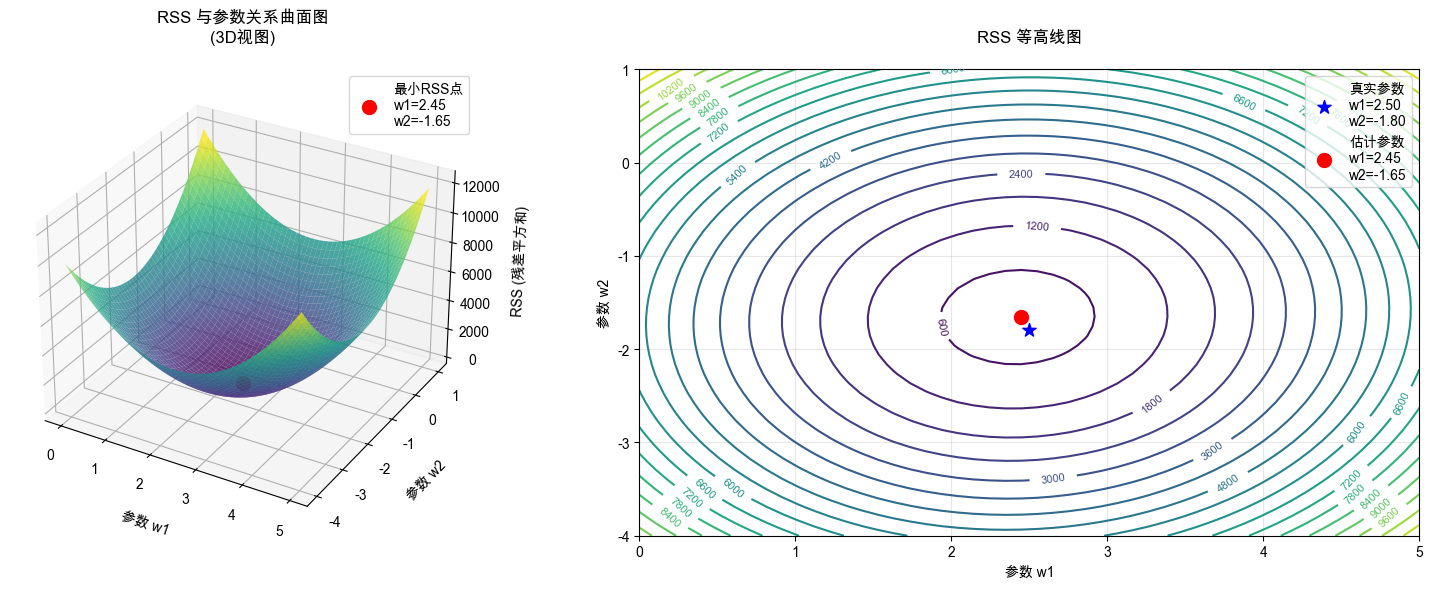
此时:
∂ E ∂ w = 0 ∂ E ∂ b = 0 \frac{\partial E}{\partial w}=0\\[10pt] \frac{\partial E}{\partial b}=0\\[10pt] ∂w∂E=0∂b∂E=0
说明什么?人生低谷就是彻底躺平
好了,下面我们就用 偏导 为 0 的条件来求解 w 和 b
偏导
它们有如下的传递关系:
w → y i ^ → u i → E b → y i ^ → u i → E w \rightarrow \hat{y_i} \rightarrow u_i \rightarrow E\\[10pt] b \rightarrow \hat{y_i} \rightarrow u_i \rightarrow E\\[10pt] w→yi^→ui→Eb→yi^→ui→E
当 w 或 b 增加一点点(eg. Δ w \Delta w Δw),最终就会引起 E 的变化( Δ E \Delta E ΔE),偏导就是保持其他变量不变,针对某个变量变化,看它结果变化,比值就是偏导,类似杠杆效应:
∂ E ∂ w = lim Δ x → 0 Δ E Δ w ∂ E ∂ b = lim Δ x → 0 Δ E Δ b \frac{\partial E}{\partial w}=\lim_{\Delta x \to 0} \frac{\Delta E}{\Delta w}\\[10pt] \frac{\partial E}{\partial b}=\lim_{\Delta x \to 0} \frac{\Delta E}{\Delta b}\\[10pt] ∂w∂E=Δx→0limΔwΔE∂b∂E=Δx→0limΔbΔE
根据链式求导法则:
∂ E ∂ w = ∑ i = 1 m ∂ E ∂ u i ⋅ ∂ u i ∂ w = ∑ i = 1 m u i ⋅ x i = ∑ i = 1 m ( w x i + b − y i ) ⋅ x i = w ∑ i = 1 m x i 2 + b ∑ i = 1 m x i − ∑ i = 1 m x i y i ∂ E ∂ b = ∑ i = 1 m ∂ E ∂ u i ⋅ ∂ u i ∂ b = ∑ i = 1 m u i = ∑ i = 1 m ( w x i + b − y i ) = w ∑ i = 1 m x i + b m − ∑ i = 1 m y i \frac{\partial E}{\partial w} =\sum\limits_{i=1}^{m}{\frac{\partial E}{\partial u_i}} \cdot {\frac{\partial u_i}{\partial w}} =\sum\limits_{i=1}^{m}{u_i\cdot x_i}\\[10pt] =\sum\limits_{i=1}^{m}{(wx_i+b-y_i)\cdot x_i}\\[10pt] =w\sum\limits_{i=1}^{m}{x_i}^2 +b\sum\limits_{i=1}^{m}{x_i} -\sum\limits_{i=1}^{m}{x_i y_i}\\[10pt] \frac{\partial E}{\partial b} =\sum\limits_{i=1}^{m}{\frac{\partial E}{\partial u_i}} \cdot {\frac{\partial u_i}{\partial b}} =\sum\limits_{i=1}^{m}{u_i}\\[10pt] =\sum\limits_{i=1}^{m}{(wx_i+b-y_i)}\\[10pt] =w\sum\limits_{i=1}^{m}{x_i}+bm-\sum\limits_{i=1}^{m}y_i\\[10pt] ∂w∂E=i=1∑m∂ui∂E⋅∂w∂ui=i=1∑mui⋅xi=i=1∑m(wxi+b−yi)⋅xi=wi=1∑mxi2+bi=1∑mxi−i=1∑mxiyi∂b∂E=i=1∑m∂ui∂E⋅∂b∂ui=i=1∑mui=i=1∑m(wxi+b−yi)=wi=1∑mxi+bm−i=1∑myi
偏导为 0 得:
∵ ∂ E ∂ w = 0 ∴ w ∑ i = 1 m x i 2 + b ∑ i = 1 m x i = ∑ i = 1 m x i y i ∵ ∂ E ∂ b = 0 ∴ w ∑ i = 1 m x i + b m = ∑ i = 1 m y i \because \frac{\partial E}{\partial w}=0\\[10pt] \therefore w\sum\limits_{i=1}^{m}{x_i}^2 +b\sum\limits_{i=1}^{m}{x_i} =\sum\limits_{i=1}^{m}{x_i y_i}\\[10pt] \because \frac{\partial E}{\partial b}=0\\[10pt] \therefore w\sum\limits_{i=1}^{m}{x_i}+bm=\sum\limits_{i=1}^{m}y_i\\[10pt] ∵∂w∂E=0∴wi=1∑mxi2+bi=1∑mxi=i=1∑mxiyi∵∂b∂E=0∴wi=1∑mxi+bm=i=1∑myi
一切皆矩阵
上面结果式可以用一个矩阵来表示:
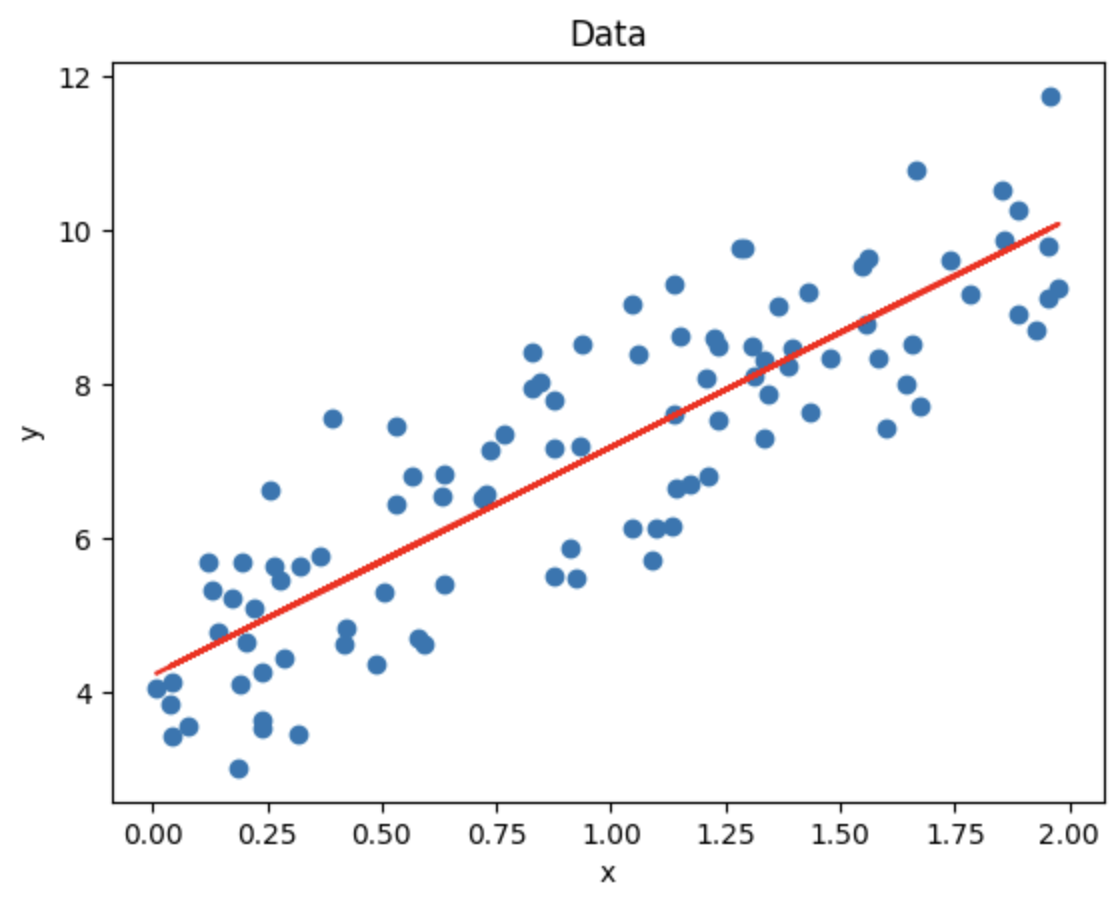
∑ i = 1 m x i 2 ∑ i = 1 m x i ∑ i = 1 m x i m \] \[ w b \] = \[ ∑ i = 1 m x i y i ∑ i = 1 m y i \] % 方括号 \\begin{bmatrix} \\sum\\limits_{i=1}\^{m}{x_i}\^2 \& \\sum\\limits_{i=1}\^{m}{x_i} \\\\\[10pt\] \\sum\\limits_{i=1}\^{m}{x_i} \& m \\end{bmatrix} \\begin{bmatrix} w\\\\\[10pt\] b \\end{bmatrix} =\\begin{bmatrix} \\sum\\limits_{i=1}\^{m}{x_i y_i}\\\\\[10pt\] \\sum\\limits_{i=1}\^{m}y_i \\end{bmatrix} i=1∑mxi2i=1∑mxii=1∑mxim wb = i=1∑mxiyii=1∑myi 令: A = \[ ∑ i = 1 m x i 2 ∑ i = 1 m x i ∑ i = 1 m x i m \] A=\\begin{bmatrix} \\sum\\limits_{i=1}\^{m}{x_i}\^2 \& \\sum\\limits_{i=1}\^{m}{x_i} \\\\\[10pt\] \\sum\\limits_{i=1}\^{m}{x_i} \& m \\end{bmatrix}\\\\\[10pt\] A= i=1∑mxi2i=1∑mxii=1∑mxim 如果 A 可逆, 可以直接求出 w,b ∵ A \[ w b \] = \[ ∑ i = 1 m x i y i ∑ i = 1 m y i \] ∴ \[ w b \] = A − 1 \[ ∑ i = 1 m x i y i ∑ i = 1 m y i \] \\because A \\begin{bmatrix} w\\\\\[10pt\] b \\end{bmatrix} =\\begin{bmatrix} \\sum\\limits_{i=1}\^{m}{x_i y_i}\\\\\[10pt\] \\sum\\limits_{i=1}\^{m}y_i \\end{bmatrix}\\\\\[10pt\] \\therefore \\begin{bmatrix} w\\\\\[10pt\] b \\end{bmatrix} =A\^{-1} \\begin{bmatrix} \\sum\\limits_{i=1}\^{m}{x_i y_i}\\\\\[10pt\] \\sum\\limits_{i=1}\^{m}y_i \\end{bmatrix} ∵A wb = i=1∑mxiyii=1∑myi ∴ wb =A−1 i=1∑mxiyii=1∑myi 厉害吧? 线性回归的问题求解通过 `矩阵运算` 就可以求出,而矩阵又可以通过 `样本数据观察` 得出,啊,瞪眼法,太美妙了! ### 最小二乘法实战 #### 准备数据 准备生成一些随机数据,大致呈线性回归 ```python import numpy as np import matplotlib.pyplot as plt # 生成一些随机数据 np.random.seed(0) x = 2 * np.random.rand(100, 1) # 理论上 w=3, b=4, 但有随机变量的作用, w,b 只能是约等于 y = 4 + 3 * x + np.random.randn(100, 1) # 可视化数据 plt.scatter(x, y) plt.xlabel('x') plt.ylabel('y') plt.title('Data') plt.show() ``` 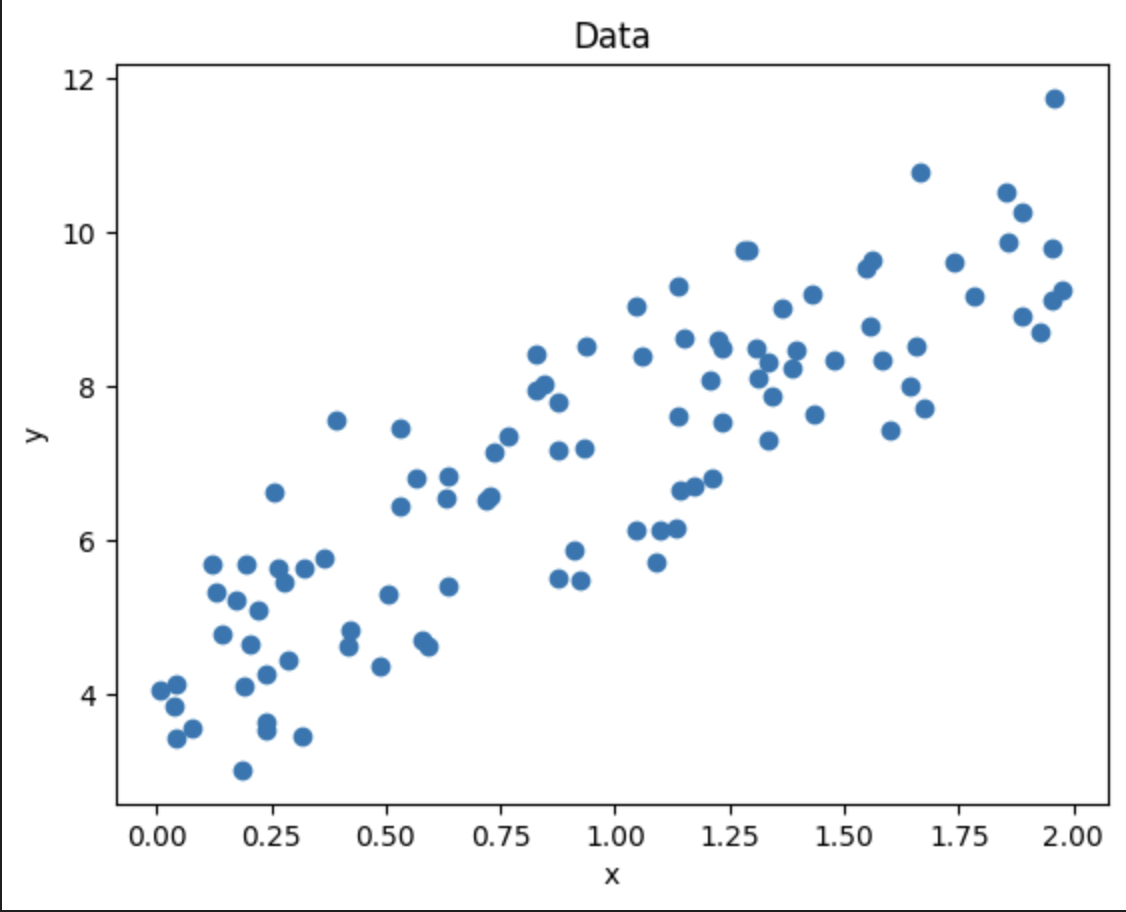 #### 计算求解 ```python # A 矩阵 [[a11,a12],[a21,a22]] a11=np.sum(x**2) a12=np.sum(x) a21=a12 a22=len(x) # Y 矩阵 y1=np.sum(x*y) y2=np.sum(y) A=np.asarray([[a11,a12],[a21,a22]]) IA=np.linalg.inv(A) Y=np.asarray([y1,y2]) W = np.dot(IA, Y) ``` #### 代入验证 ```python w=W[0] b=W[1] # 对应解示例: (2.968467510701019, 4.222151077447229) print(w,b) y_pred = w * x + b # 可视化数据 plt.scatter(x, y) plt.plot(x, y_pred, color='red') plt.xlabel('x') plt.ylabel('y') plt.title('Data') plt.show() ```