题目链接
题目描述

题目解析
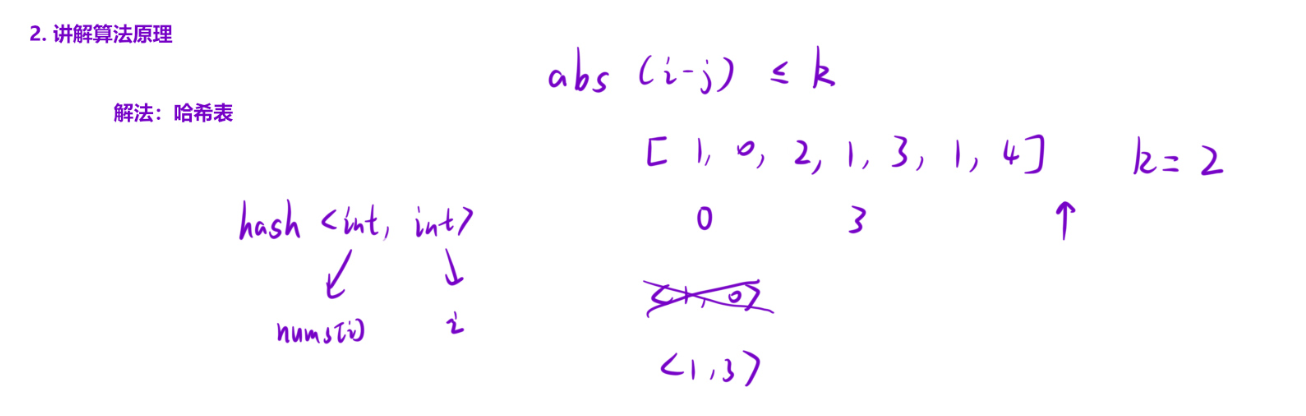
代码逐行解析
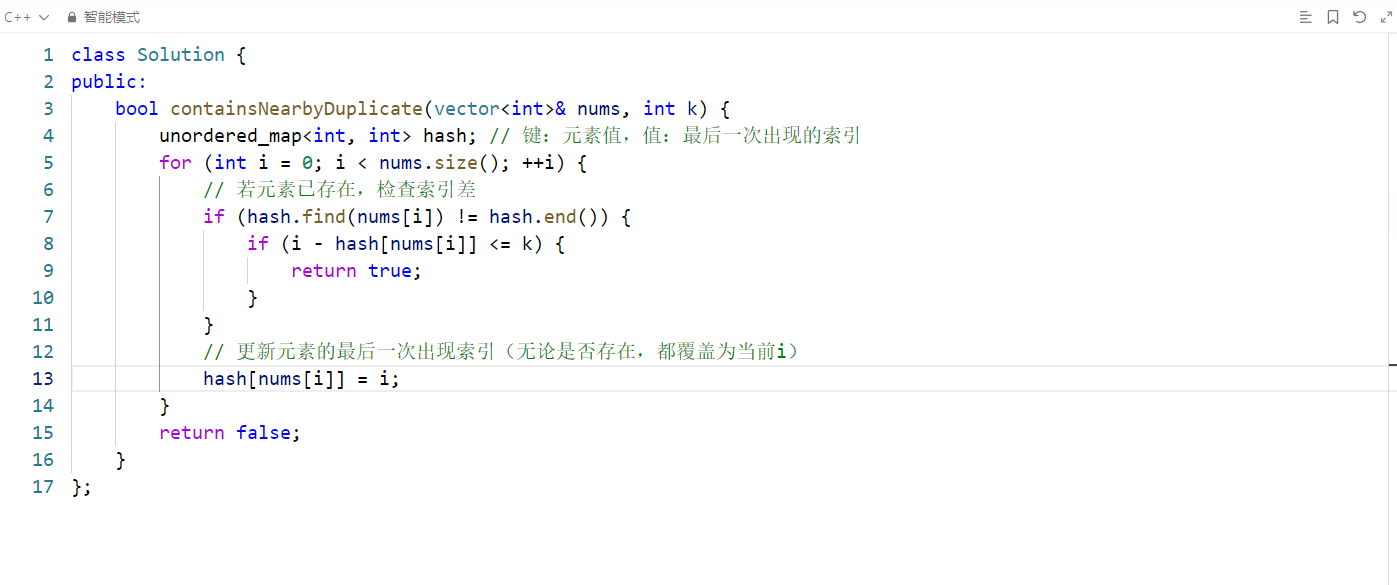
这段代码通过哈希表记录元素最后一次出现的索引,遍历数组时实时检查是否存在 "值相等且索引差≤k" 的元素对,是解决该问题的最优解法之一。以下是逐行详细解析:
cpp
class Solution {
public:
bool containsNearbyDuplicate(vector<int>& nums, int k) {
// 1. 定义哈希表:键=数组元素值,值=该元素最后一次出现的索引
unordered_map<int, int> hash;
// 2. 遍历数组,i为当前元素的索引
for (int i = 0; i < nums.size(); ++i) {
// 3. 检查当前元素是否已在哈希表中(即之前出现过)
if (hash.find(nums[i]) != hash.end()) {
// 4. 若存在,计算当前索引与最后一次出现索引的差值
// 若差值≤k,满足题目条件,直接返回true
if (i - hash[nums[i]] <= k) {
return true;
}
}
// 5. 无论当前元素是否存在于哈希表中,都更新其索引为当前i
// (核心逻辑:保留最新索引,最大化后续满足"索引差≤k"的可能性)
hash[nums[i]] = i;
}
// 6. 遍历结束未找到符合条件的元素对,返回false
return false;
}
};核心逻辑拆解
1. 哈希表的作用
哈希表 hash 的核心是用空间换时间:
- 避免暴力枚举所有元素对(暴力法时间复杂度 O (n²),对于 n=10⁵会超时);
- 快速查询 "当前元素是否出现过" 以及 "最后一次出现的索引"(哈希表查询 / 更新的平均时间复杂度为 O (1))。
2. 关键操作:更新索引
代码第 5 行 hash[nums[i]] = i 是核心,需重点理解:
- 若元素首次出现:哈希表中无该键,直接存入 "值→索引" 的映射;
- 若元素非首次出现:即使本次索引差 > k,也需覆盖为当前索引(因为后续遍历的元素索引更大,保留最新索引能让 "索引差" 更小,更易满足≤k 的条件)。
3. 索引差的简化计算
题目要求 abs(i-j) ≤ k,但由于遍历是按索引递增顺序 (i 从 0 到 n-1),当前索引 i 一定大于之前的索引 j,因此只需计算 i - hash[nums[i]],无需取绝对值,简化了逻辑。
示例推演(以示例 1 为例)
示例 1:nums = [1,2,3,1], k=3
| 遍历索引 i | 当前元素 nums [i] | 哈希表状态(更新前) | 索引差计算 | 哈希表状态(更新后) | 结果 |
|---|---|---|---|---|---|
| 0 | 1 | 空 | - | {1:0} | - |
| 1 | 2 | {1:0} | - | {1:0, 2:1} | - |
| 2 | 3 | {1:0, 2:1} | - | {1:0, 2:1, 3:2} | - |
| 3 | 1 | {1:0, 2:1, 3:2} | 3-0=3 ≤3 | - | 返回 true |
复杂度分析
| 维度 | 复杂度 | 说明 |
|---|---|---|
| 时间复杂度 | O(n) | 遍历数组一次,哈希表操作均为 O (1)(平均) |
| 空间复杂度 | O(n) | 最坏情况(所有元素唯一),哈希表存储 n 个键值对 |
边界情况处理
- k=0:要求两个元素索引完全相同,但题目要求 "不同的索引 i 和 j",因此 k=0 时直接返回 false(代码会自然处理:若元素重复,i-j≥1>0,不会触发返回 true);
- 数组长度 = 1:无两个不同索引,直接返回 false;
- 重复元素索引差刚好 = k :例如
nums=[1,2,1], k=2,i=2 时,2-0=2≤2,返回 true。
优化点(可选)
若想进一步优化空间,可改用滑动窗口 + 哈希集合(空间复杂度 O (k)),但该代码的优势是实现更简洁,且在大多数场景下效率已足够。
题目链接
题目描述

题目解析
字母异位词分组(groupAnagrams)代码解析
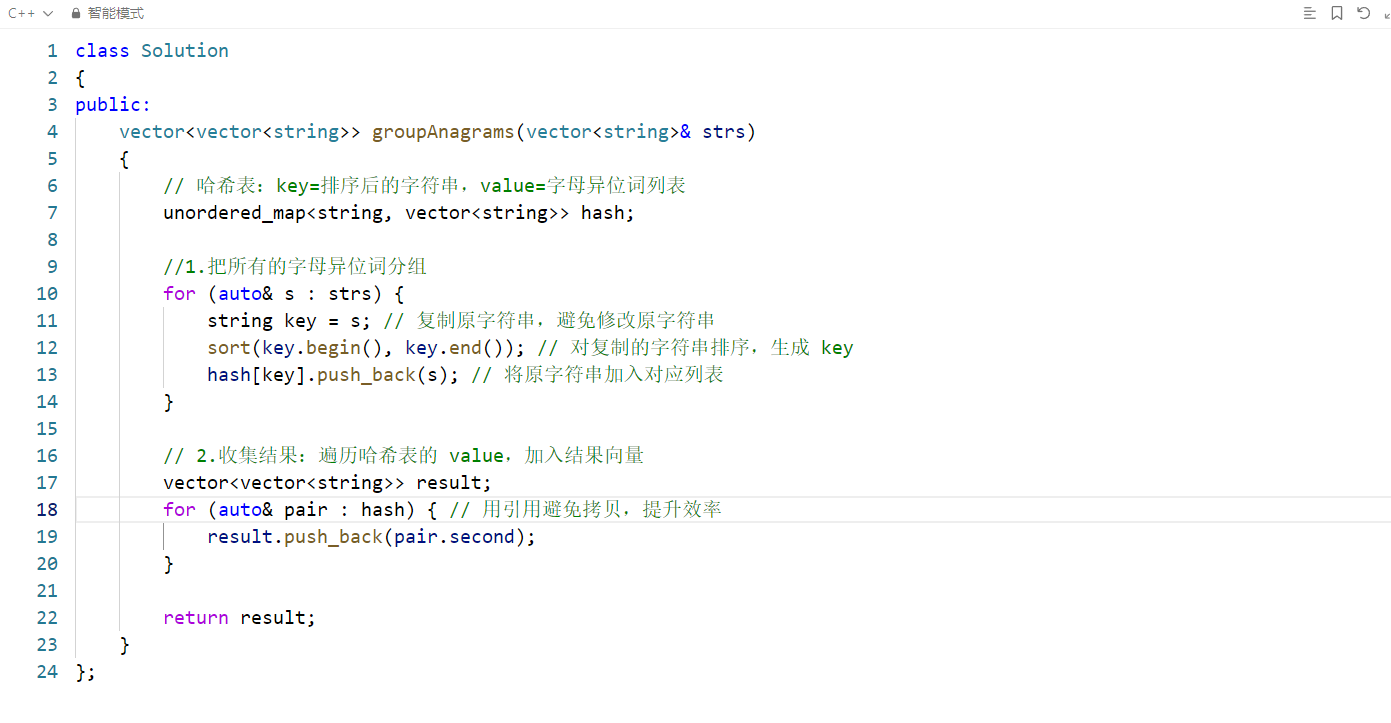
这道题的核心是识别字母异位词(由相同字母组成但排列不同的字符串),并将它们分组。代码通过「哈希表 + 字符串排序」的思路高效解决了问题,以下是逐部分解析:
一、核心思路
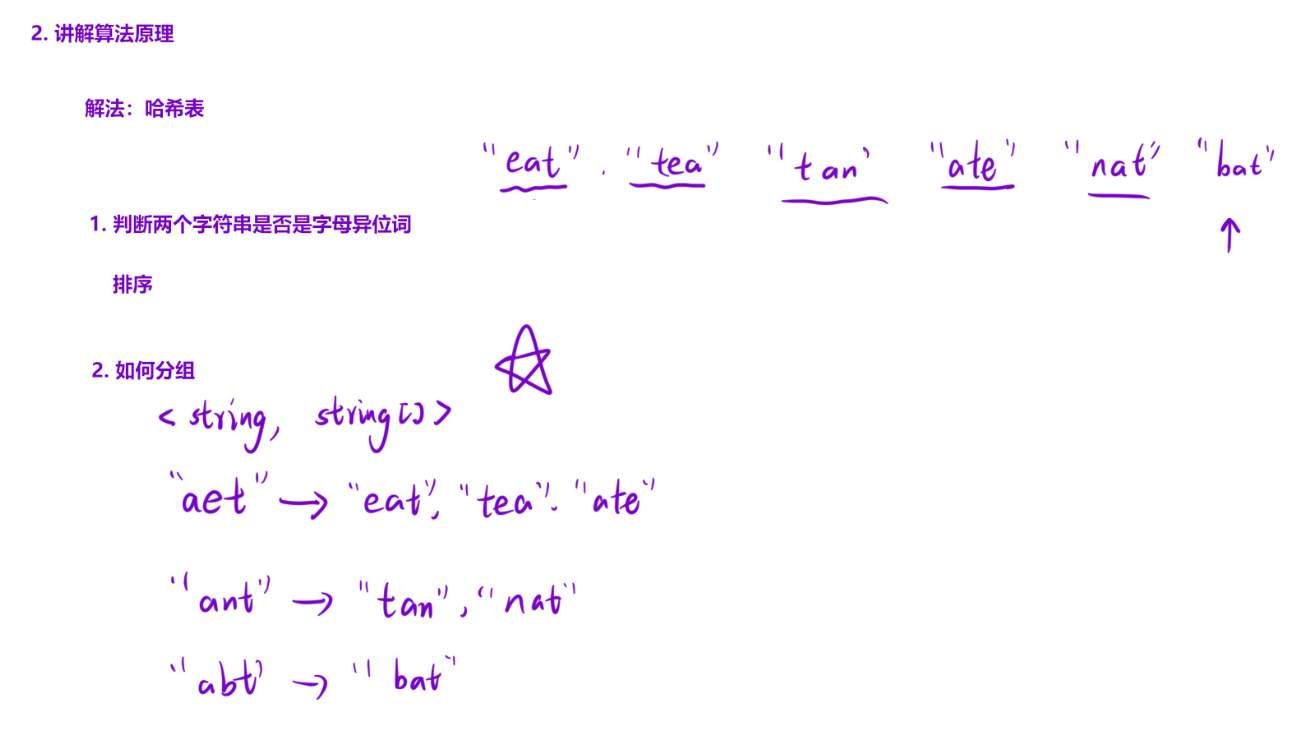
字母异位词的本质特征:排序后字符串完全相同 。例如:"eat"、"tea"、"ate" 排序后都是 "aet",因此可以用「排序后的字符串」作为哈希表的 key,原字符串作为 value(列表形式),最终将哈希表的 value 收集为结果即可。
二、代码逐行解析
cpp
class Solution
{
public:
vector<vector<string>> groupAnagrams(vector<string>& strs)
{
// 哈希表:key=排序后的字符串,value=该key对应的所有字母异位词
unordered_map<string, vector<string>> hash;- 哈希表定义 :
key:字符串类型,存储「排序后的字符串」(作为异位词的唯一标识);value:字符串列表,存储所有和key匹配的原字符串(即同一组异位词);- 选择
unordered_map而非map:哈希表查询 / 插入时间复杂度 O (1),比红黑树(O (logn))效率更高。
cpp
// 1. 遍历所有字符串,完成分组
for (auto& s : strs) {
string key = s; // 复制原字符串,避免修改原数组的strs
sort(key.begin(), key.end()); // 排序生成key(异位词的统一标识)
hash[key].push_back(s); // 将原字符串加入对应分组
}- 遍历分组逻辑 :
auto& s : strs:用引用遍历原数组,避免拷贝开销;string key = s:复制原字符串,因为排序会修改字符串,不能直接操作原字符串;sort(key.begin(), key.end()):对key排序(默认按字符 ASCII 升序),例如"tea"→"aet";hash[key].push_back(s):将原字符串s加入key对应的列表,完成分组。
cpp
// 2. 收集哈希表中的分组,生成最终结果
vector<vector<string>> result;
for (auto& pair : hash) { // 引用遍历,避免拷贝哈希表的value
result.push_back(pair.second);
}
return result;
}
};- 结果收集 :
- 初始化结果数组
result(二维字符串数组); - 遍历哈希表的每一个键值对
pair:pair.first:排序后的key(无需使用);pair.second:同一组异位词的列表;
- 将所有分组列表加入
result,最终返回。
- 初始化结果数组
三、复杂度分析
| 维度 | 复杂度 | 说明 |
|---|---|---|
| 时间复杂度 | O(n * k logk) | n = 字符串数量,k = 单个字符串的最大长度;排序每个字符串 O (k logk),共 n 次;哈希表操作 O (1) 均摊。 |
| 空间复杂度 | O(n * k) | 哈希表存储所有字符串(n 个,每个长度 k),结果数组不额外计算。 |
四、关键细节与优化点
- 避免修改原字符串 :必须复制
s到key再排序,否则会破坏输入数组strs。 - 引用遍历提升效率 :
for (auto& s : strs)和for (auto& pair : hash)用引用避免拷贝,尤其当字符串较长时效果显著。 - 哈希表的键选择 :除了排序后的字符串,也可以用「字符计数」作为键(例如
a:1,e:1,t:1),时间复杂度可优化为 O (n*k)(无需排序),但实现稍复杂。
五、示例验证
输入:strs = ["eat","tea","tan","ate","nat","bat"]
- 遍历分组:
"eat"→ key"aet"→ 列表["eat"]"tea"→ key"aet"→ 列表["eat","tea"]"tan"→ key"ant"→ 列表["tan"]"ate"→ key"aet"→ 列表["eat","tea","ate"]"nat"→ key"ant"→ 列表["tan","nat"]"bat"→ key"abt"→ 列表["bat"]
- 收集结果:
[["eat","tea","ate"],["tan","nat"],["bat"]](顺序不影响正确性)。
该代码逻辑清晰、效率均衡,是解决字母异位词分组的经典解法。