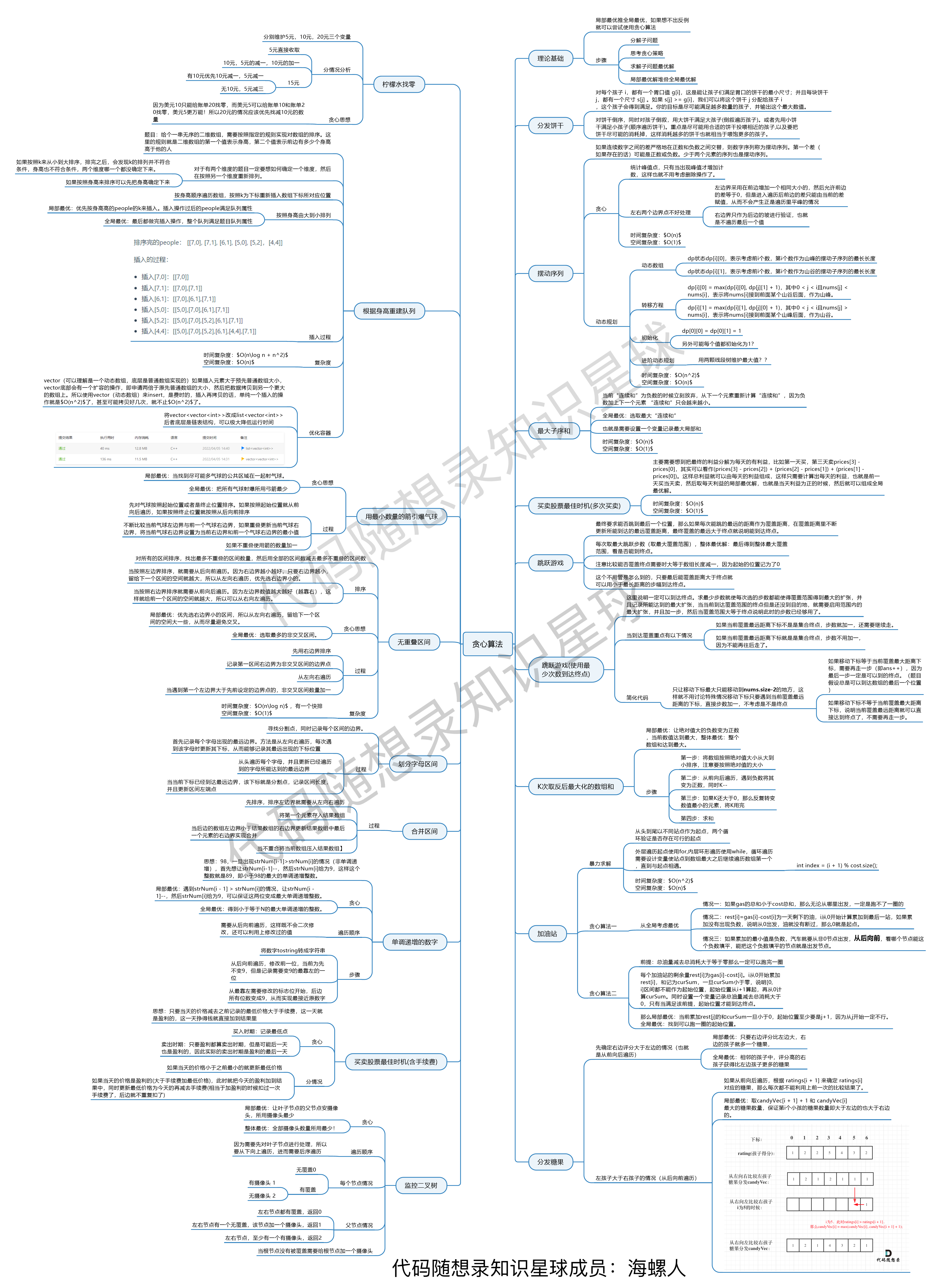
动规是由前一个状态推导出来的,而贪心是局部直接选最优的。
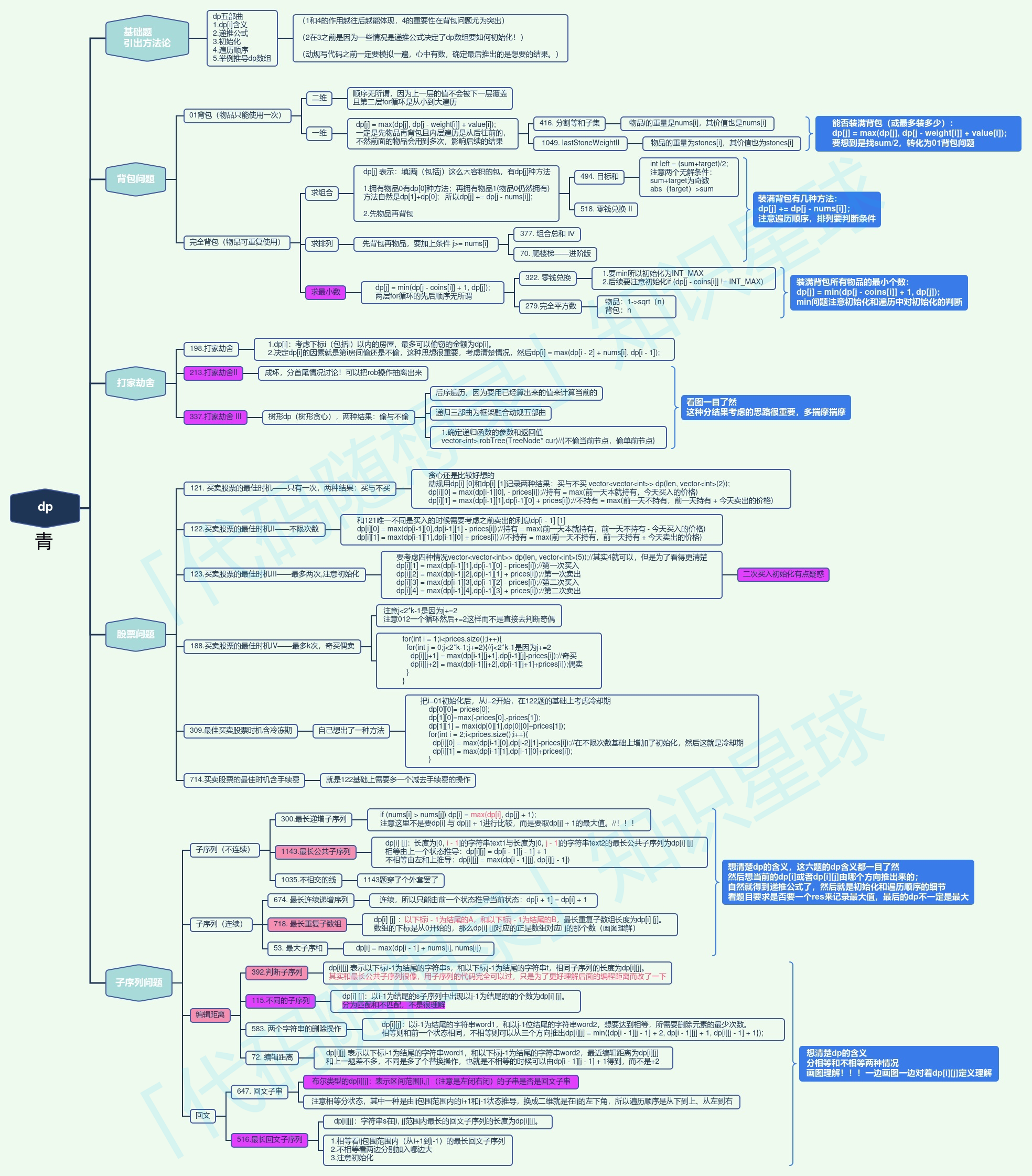
对于动态规划问题可以拆解成以下五步曲:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
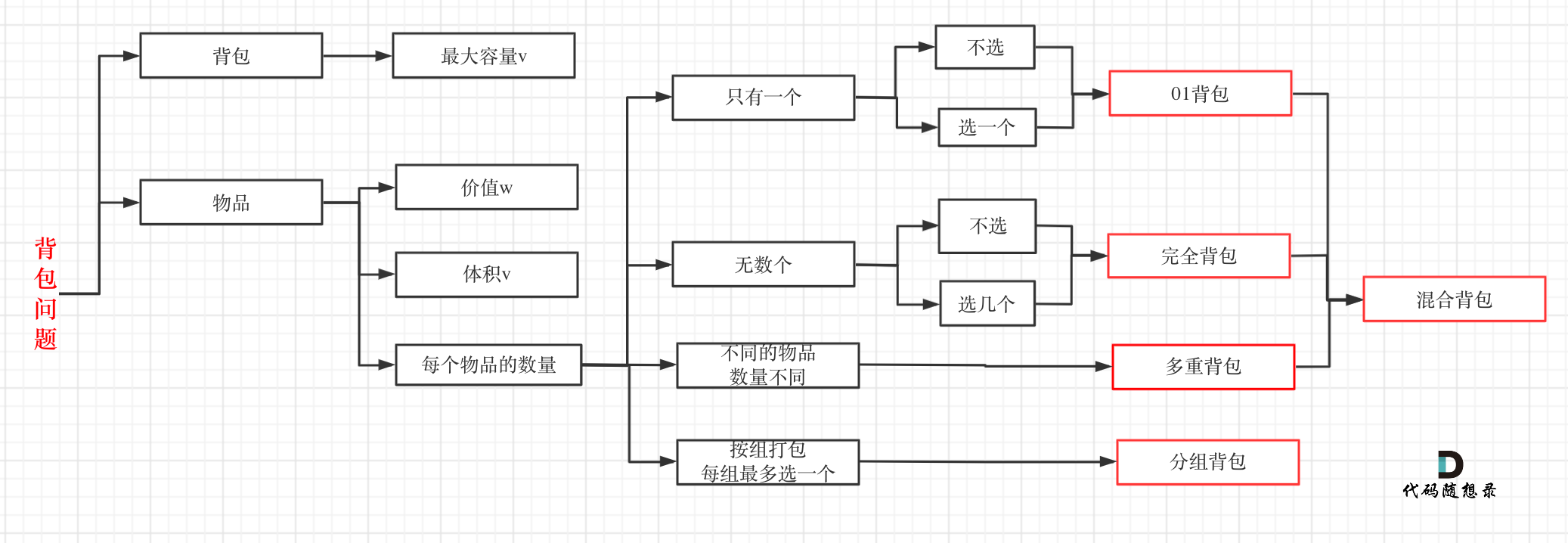
背包问题
二维dp数组
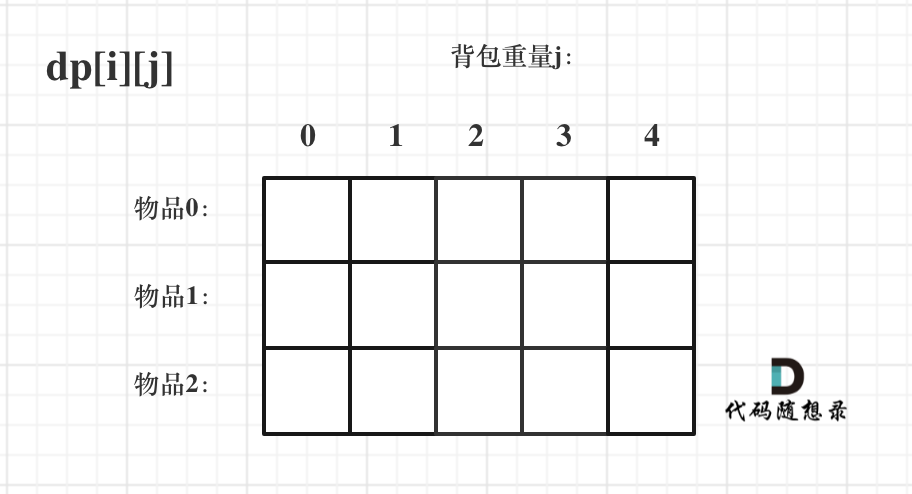
横轴表示物品编号,纵轴表示背包的重量
-
不放物品i:背包容量为j,里面不放物品i的最大价值是dp[i - 1][j]。
-
放物品i:背包空出物品i的容量后,背包容量为j - weight[i],dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
dp[j]容量为j的背包所能装的最大重量
一维dp数组递推公式 :dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
目标和
要使表达式结果为target,既然为target,那么就一定有 left组合 - right组合 = target。left + right = sum,而sum是固定的。right = sum - left。left - (sum - left) = target 推导出 left = (target + sum)/2 。target是固定的,sum是固定的,left就可以求出来。此时问题就是在集合nums中找出和为left的组合
完全背包
递推公式:dp[i][j] = max(dp[i - 1][j], dp[i][j - weight[i]] + value[i]);
-
不放物品i:背包容量为j,里面不放物品i的最大价值是dp[i - 1][j]。
-
放物品i:背包空出物品i的容量后,背包容量为j - weight[i],dp[i][j - weight[i]] 为背包容量为j - weight[i]且不放物品i的最大价值,那么dp[i][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值