北京大学国家发展研究院 经济学辅修 经济学原理课程笔记（第三课 需求与供应弹性）

文章目录

• [第三课 需求与供应弹性](#第三课 需求与供应弹性)
• • 弹性的基本概念
  • • 弹性的定义
    • 弹性的数学表述
    • 弹性的应用优势
  • 需求的价格弹性
  • • 需求价格弹性的定义和公式
    • 需求价格弹性与价格水平的关系
    • 需求弹性的两种计算方法
    • 影响需求价格弹性的因素
    • • 替代品的可得性
      • 产品的定义范围
      • 时间范围的长短
    • 需求弹性与需求曲线
    • 需求价格弹性与总销售收入
    • • 需求弹性的三种类型
      • 价格变动如何影响总销售收入
    • 其他类型的需求弹性
    • • 需求的收入弹性
      • 需求的交叉价格弹性
  • 供给的价格弹性
  • • 供给价格弹性的定义
    • 供给的区间价格弹性
    • 影响供给价格弹性的因素
    • 供给曲线形状与价格弹性
  • 从弹性角度观察市场变化（应用案例）

第三课 需求与供应弹性

弹性的基本概念

弹性的定义

弹性衡量一个变量对另一个变量变化的敏感程度。经济学中经常关心一个变量（比如价格）发生变化后，另一个相关的变量（比如需求量）会跟着变化多少。弹性就是用来描述这种跟着变化的程度大小的指标。

弹性的数学表述

弹性的标准定义：因变量变化的百分比，除以自变量变化的百分比。用公式来表达就是：

弹性 = （因变量变化的百分比） / （自变量变化的百分比） 弹性 = （因变量变化的百分比）/（自变量变化的百分比） 弹性=（因变量变化的百分比）/（自变量变化的百分比）

公式解读：自变量每变化一个百分点，因变量会相应地变化几个百分点。

弹性的应用优势

• 原因一（弹性无量纲便于比较）。

  • 思考一个问题：是房子对价格的变化更敏感，还是苹果对价格的变化更敏感？

  • 假设房价上涨1000元，房屋成交量下降了10套。同时，苹果价格上涨1元，苹果销量下降了500斤。不能直接比较"10套"和"500斤"，因为单位完全不同，一个是"套"，一个是"斤"。也没法直接比较"1000元"的房价涨幅和"1元"的苹果价格涨幅，因为基础价格差异巨大。用绝对数值的变化来衡量敏感度得不出有意义的结论。

  • 但是，百分比是一个相对值，本身没有单位。比如，我们可以计算出房价上涨1%时，房屋成交量下降了0.5%；苹果价格上涨10%时，苹果销量下降了20%。这样，-0.5% / 1% = -0.5 和 -20% / 10% = -2 这两个弹性的数值就可以直接比较了。

  • 弹性是无量纲的，所以可以用来衡量和比较各种不同商品、不同市场之间的敏感程度。

• 原因二（斜率与度量单位有关）。

  • 在需求曲线或者供应曲线上，某一点的斜率也表示了两个变量之间的变化关系。但斜率的数值会随着使用的单位变化而变化。
  • 还用苹果的例子。假设我们用"元/斤"来衡量价格，用"斤"来衡量数量。计算出的斜率可能是-500。如果换个单位，用"元/公斤"来衡量价格（1公斤=2斤），用"公斤"来衡量数量。那么同样的需求关系计算出的斜率数值就会改变。
  • 斜率这个指标不稳定，换个单位它的数值就变了。消费者的行为是客观存在的，不应该因为我们用不同的尺子去量而改变。而弹性，是一个不受度量单位影响的客观反映敏感程度的指标。

需求的价格弹性

需求价格弹性的定义和公式

需求价格弹性的含义：衡量一种商品的需求量，对于其自身价格变化的敏感程度。公式表达：
需求的价格弹性 = 需求量变化的百分比 / 价格变化的百分比 需求的价格弹性 = 需求量变化的百分比 / 价格变化的百分比 需求的价格弹性=需求量变化的百分比/价格变化的百分比

因为价格和需求量通常是反向变动的（价格上升，需求量下降），所以计算出的需求价格弹性通常是一个负数。但在讨论中常常省略负号，直接使用绝对值。

需求价格弹性与价格水平的关系

对于一条线性的需求曲线（也就是一条直线），价格越高的地方，需求价格弹性的绝对值就越大。

• 在直线的左上方区域：这里的特点是"价格高，需求量小"。因为价格（P）本身已经很高了，所以即使价格再上涨一点点，上涨的"百分比"（ΔP/P）也不会太大。但与此同时，因为价格高，愿意且能够购买的消费者本来就少（Q很小），价格再一上涨，可能会导致很多人放弃购买，所以需求量下降的"百分比"（ΔQ/Q）会非常大。一个很大的分子（需求量变化百分比）除以一个较小的分母（价格变化百分比），得出的弹性绝对值自然就很大。说明在高价位区间，消费者对价格变动非常敏感。
• 在直线的右下方区域：这里的特点是"价格低，需求量大"。因为价格（P）本身已经很低了，所以即使价格只下降一点点，下降的"百分比"（ΔP/P）也可能会比较大。但因为价格已经很便宜，几乎所有想买的人都已经买了（Q很大），再降价吸引来的新需求量可能有限，所以需求量增加的"百分比"（ΔQ/Q）相对较小。一个较小的分子除以一个较大的分母，得出的弹性绝对值就比较小。这说明在低价位区间，消费者对价格变动不太敏感。

结论：沿同一条线性需求曲线从高价位向低价位移动，需求价格弹性的绝对值递减。

需求弹性的两种计算方法

点弹性 ：当价格的变化非常非常小，小到几乎可以看作是需求曲线上一个点的瞬间变化时，使用点弹性来精确衡量该点的弹性。当 ΔP 趋向于0时，ΔQ/ΔP 就变成了需求量 Q 对价格 P 的导数，也就是 dQ/dP。所以点弹性的公式是：
( d Q / d P ) ∗ ( P / Q ) (dQ/dP) * (P/Q) (dQ/dP)∗(P/Q)

• dQ / dP：需求曲线在该点的斜率的倒数，反映了数量随价格变化的瞬时速度。

• P / Q：这是该点本身的价格与需求量的比值。

点弹性给出了在某一个特定的价格水平上，需求对价格变动的精确敏感度。

区间弹性与中点法：当价格的变化幅度较大时，如价格从 10 元涨到 12 元，用最开始的 (ΔQ/Q) / (ΔP/P) 公式会遇到一个问题：分母中的 P 和 Q，到底应该用变化前的数值还是变化后的数值？例如，价格从10 元§涨到 12元(P')，需求量从 100 个(Q)降到 80 个(Q')。

• 如用初始值（P=10, Q=100）作基准，价格变化百分比 (12-10)/10 = 20%，需求量变化百分比 (80-100)/100 = -20%，弹性是 -1。
• 如用终点值（P'=12, Q'=80）作基准，价格变化百分比 (12-10)/12 ≈ 16.7%，需求量变化百分比 (80-100)/80 = -25%，弹性是 -1.5。

同一价格区间的变化算出了两个不同的弹性值，这显然不理想。为解决这个问题，经济学家提出了中点法。中点法的核心思想是：不用初始值也不用终点值作基准，而是用两个点的中点值（也就是平均值）作基准。所以区间弹性的公式就是：

• 分子（需求量变化的百分比）= 需求量变化值 / 平均需求量 = (Q' - Q) / ((Q' + Q)/2)
• 分母（价格变化的百分比）= 价格变化值 / 平均价格 = (P' - P) / ((P' + P)/2)

把这两部分合在一起同时消去分母中的"/2"，就得到了公式：
区间弹性 = [ ( Q ′ − Q ) / ( Q ′ + Q ) ] / [ ( P ′ − P ) / ( P ′ + P ) ] 区间弹性 = [(Q' - Q) / (Q' + Q)] / [(P' - P) / (P' + P)] 区间弹性=[(Q′−Q)/(Q′+Q)]/[(P′−P)/(P′+P)]

中点法的好处是，无论价格是从10元涨到12元，还是从12元跌回10元，计算出的弹性数值都是一样的，保证了结果的一致性。

影响需求价格弹性的因素

替代品的可得性

影响需求价格弹性最核心的因素。

• 基本原理：一种商品的可替代品越多、越相似，它的需求价格弹性就越大。
• 内在逻辑：如果一件商品涨价了，但市场上有很多功能相似、价格不变的其他商品可供选择，那么消费者会很轻松地放弃原来的商品，转而购买它的替代品。这种行为意味着消费者对价格的变化非常敏感，也就是弹性大。反之，如果一件商品没什么好的替代品，甚至是独一无二的，那么即使它涨价了，消费者也不得不接受。这种情况下消费者对价格就不那么敏感，弹性就小。
• 常见例子 ：
  • 低可替代性（弹性小）：电力和自来水。如果电费或水费上涨，很难找到有效的替代品来满足日常生活所需。总不能为了省电就都点蜡烛，或者为了省水就不洗澡。由于缺少替代方案，对这类商品价格变化的反应就很有限，需求弹性非常小。
  • 高可替代性（弹性大）：竞争行业的产品。假设常喝的某个牌子的矿泉水涨价了，可以很方便地换成其他任何一个牌子的矿泉水，因为它们之间的差别很小。正是因为有大量相似的替代品存在，特定品牌矿泉水的需求弹性就非常大。

产品的定义范围

上一个因素的延伸，说明"圈定"一个商品的方式会直接影响它的弹性。

• 基本原理：对一个产品的定义范围越宽泛，它的需求价格弹性就越小；定义范围越狭窄，弹性就越大。
• 内在逻辑：定义的范围，其实就决定了我们是在"圈内"还是在"圈外"寻找替代品。
• 常见例子 ：品类需求弹性与品牌需求弹性。
  • 宽泛的定义（品类）：比如"饮料"。如果考察的是整个"饮料"市场的需求弹性，当所有饮料的平均价格都上涨时，消费者能找到的替代品可能只有自来水。因为替代品很少，所以"饮料"这个大类的需求弹性就比较小。
  • 狭窄的定义（品牌）：比如"某个特定品牌的饮料"。如果只是这一个牌子的饮料涨价了，其他牌子的价格不变，那么它的替代品就非常多：其他所有牌子的饮料都是它的替代品。因此，特定品牌饮料的需求弹性就会非常大。

时间范围的长短

这个因素强调了消费者的反应和调整是需要时间的。

• 基本原理：时间范围越长，需求价格弹性就越大；时间范围越短，弹性就越小。
• 内在逻辑：当价格突然变化时人们在短期内往往难以改变消费习惯或依赖。但如果把时间拉长，就有更充分的机会去寻找替代品、改变消费行为，甚至发展新技术。
• 常见例子 ：
  • 汽油：如果今天汽油价格突然上涨了20%，明天你大概率还是要开同样的车走同样的路去上班，因为没有别的选择。短期内，对汽油的需求几乎没什么变化，弹性非常小。但是，如果油价在未来几年都维持在高位，人们可能会开始选择乘坐公共交通，或者在下次换车时，会优先考虑购买电动车或更省油的汽车。这些长期的行为调整，使得汽油在长期内的需求弹性要远大于短期。
  • 铜：这个例子是从工业生产的角度看的。如果铜价突然上涨，一个正在建造楼房的建筑公司短期内只能接受高价，因为它需要铜来制造电线和管道，项目不能停工。短期需求弹性小。但如果铜价长期居高不下，工程师和设计师们就会开始研发和使用铜的替代材料。因此，长期来看，工业上对铜的需求弹性也更大。

需求弹性与需求曲线

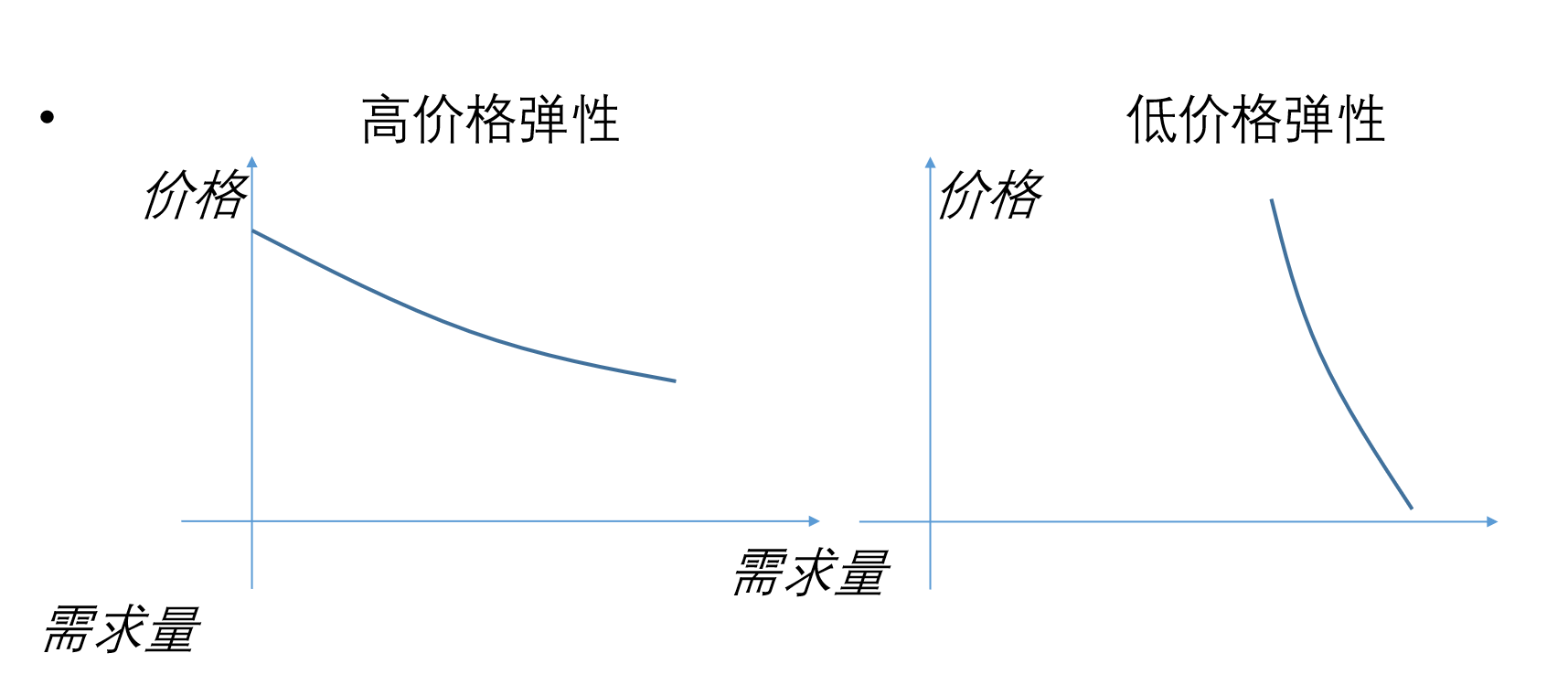
• 高价格弹性的需求曲线（左图）：

  • 形状特征：曲线的形态相对平坦。
  • 经济学含义：价格（纵坐标）发生一个很小的变动，比如稍微下降一点，对应的需求量（横坐标）会向右移动很长一段距离，说明需求量大幅增加。反之，如果价格稍微上涨一点，需求量会大幅减少。
  • 结论：价格的微小变化引起需求量的巨大变化，消费者对价格高度敏感。因此，一条相对平坦的需求曲线代表了高价格弹性，常用来描述那些拥有大量替代品的商品（比如特定品牌的矿泉水）或者奢侈品。

• 低价格弹性的需求曲线（右图）：

  • 形状特征：曲线的形态相对陡峭。
  • 经济学含义：即使价格（纵坐标）发生巨大的变动，比如大幅下降，对应的需求量（横坐标）也仅向右移动了很短的距离，需求量的增加非常有限。反之，即使价格大幅上涨，需求量也只略微减少。
  • 结论：价格的巨大变化只引起需求量的微小变化，说明消费者对价格不敏感。因此，一条相对陡峭的需求曲线代表了低价格弹性，常用来描述那些缺少替代品的生活必需品，比如电力、自来水或者救命的药品。

• 一个重要的总结和提醒：

  • 在同一个坐标系下，需求曲线越平坦，弹性越大；需求曲线越陡峭，弹性越小。
  • 虽然曲线的平坦或陡峭程度可以提供关于弹性大小的直观感受，但它和斜率在数学上是两个不同的概念。对于一条斜率不变的直线需求曲线，其上每一点的弹性都是不一样的。这里的"平坦"和"陡峭"更多用来比较两条不同需求曲线的弹性特征，而不是用来描述一条曲线上各点弹性的绝对值的。

需求价格弹性与总销售收入

明确一个基本公式：
总销售收入 = 商品价格 ( P ) × 销售数量 ( Q ) 总销售收入 = 商品价格 (P) × 销售数量 (Q) 总销售收入=商品价格(P)×销售数量(Q)

当讨论调整价格时，公式里有两个变量在同时变动。价格（P）上升，会导致销售数量（Q）下降。它们的乘积（总销售收入）是会上升还是下降取决于 P 和 Q 哪一个变化的力量更大。而这个力量的大小就是由需求价格弹性来衡量的。

需求弹性的三种类型

根据需求价格弹性数值的大小（通常看绝对值），我们可以把需求分为三类：

• 富有弹性：需求的价格弹性大于 1 。意味着需求量变化的百分比大于价格变化的百分比。消费者对价格非常敏感。
• 缺乏弹性：需求的价格弹性小于 1 。意味着需求量变化的百分比小于价格变化的百分比。消费者对价格不很敏感。
• 单位弹性：需求的价格弹性等于 1 。意味着需求量变化的百分比正好等于价格变化的百分比。价格和需求量的变化刚好抵消。

价格变动如何影响总销售收入

• 情况一：当需求是富有弹性时（弹性 > 1）：

  • 内在逻辑：这种情况下需求量变化的力量超过了价格变化的力量。

  • 决策后果：

    • 如果商家选择提高价格：比如价格只提高了10%，但因为消费者非常敏感，需求量可能会大幅下降30%。虽然每件商品卖得更贵了，但卖出去的数量少了太多，最终导致总销售收入下降。

    • 如果商家选择降低价格：比如价格降低了10%，大量的消费者被吸引过来，导致需求量可能激增30%。这种"薄利多销"的策略，使得销售量增加带来的收入超过了单价降低的损失，最终导致总销售收入增加。

  • 结论：对于富有弹性的商品，降价会增加总收入，涨价会减少总收入。

• 情况二：当需求是缺乏弹性时（弹性 < 1）：

  • 内在逻辑：这种情况下价格变化的力量超过了需求量变化的力量。

  • 决策后果：

    • 如果商家选择提高价格：比如价格提高了 20%，但因为消费者对商品很依赖（比如这是生活必需品），需求量可能只下降了 5%。在这种情况下，价格上涨带来的收入增加超过了销量微弱下滑造成的损失，最终导致总销售收入增加。

    • 如果商家选择降低价格：降价不能有效刺激需求。价格降低 20% 可能只换来 5% 的销量增长，总销售收入会下降。

  • 结论：对于缺乏弹性的商品，涨价会增加总收入，降价会减少总收入。

• 情况三：当需求是单位弹性时（弹性 = 1）：

  • 内在逻辑：价格变化的力量和需求量变化的力量正好完全相等，相互抵消。

  • 决策后果：无论商家是提高价格还是降低价格，总销售收入都保持不变。

  • 结论：对于单位弹性的商品，价格变动不影响总收入。

其他类型的需求弹性

需求的收入弹性

• 定义：衡量当消费者的收入发生变化时一种商品的需求量会如何变化。
• 公式：需求的收入弹性 = 需求量变化的百分比 / 收入变化的百分比
• 作用 ：收入弹性的正负号，可以帮助我们判断一个商品属于哪种类型。
  • 收入弹性为负（< 0） ：这类商品被称为"劣等品"或"低档品"。
    • 内在逻辑：当人们的收入增加时反而会减少对这类商品的购买，因为他们有能力去消费更好的替代品了。例如，方便面或者长途汽车票。当收入很低时，可能会经常消费它们；但当收入提高后，可能会选择更健康的食物更快速的出行方式，从而减少对它们的需求。
  • 收入弹性为正（> 0） ：这类商品被称为"正常品"。
    • 内在逻辑：最常见的情况。当人们的收入增加时，会对这类商品购买得更多。大部分商品都属于正常品。
  • 在正常品中，我们还可以进一步细分：当收入弹性大于1时，这类正常品又被称为"奢侈品"。
    • 内在逻辑：这意味着，需求量增加的百分比，要大于收入增加的百分比。比如，你的收入增加了10%，但你对海外旅游的需求可能会增加30%。奢侈品不是生活的必需，但随着收入的提高，人们会不成比例地增加对它们的消费。

需求的交叉价格弹性

• 定义：衡量当"产品 2"的价格发生变化时，"产品 1"的需求量会如何变化。注意，这里涉及了两种不同的商品。
• 公式：需求的交叉价格弹性 = 产品 1 的需求量变化的百分比 / 产品 2 的价格变化的百分比。
• 作用 ：交叉价格弹性的正负号，可以帮助我们判断两种商品之间的关系。
  • 交叉价格弹性为正（> 0） ：两种商品互为替代品。
    • 内在逻辑：当产品 2 的价格上升时，消费者会觉得它变贵了，转而去购买和它功能相似的产品 1，导致产品 1 的需求量增加。一个价格上升，另一个需求量也上升，变化方向相同，所以结果为正。典型例子是可口可乐和百事可乐。
  • 交叉价格弹性为负（< 0） ：两种商品互为互补品。
    • 内在逻辑：互补品是需要搭配在一起使用的商品。当产品 2 的价格上升时，人们对产品 2 的消费会减少，连带着对与之配套的产品 1 的需求量也减少了。一个价格上升，另一个需求量反而下降，变化方向相反，所以结果为负。典型的例子是汽车和汽油。如果汽油价格暴涨，买车的需求可能就会下降。

供给的价格弹性

供给价格弹性的定义

• 含义：衡量一种商品的供给量对自身价格变化的敏感程度。也就是当商品价格上涨时生产者愿意并且能够增加多少产量来供应市场。
• 公式：供给的价格弹性 = 供给量变化的百分比 / 价格变化的百分比
• 注意事项：由于价格上升通常会激励生产者增加供给（供给曲线向右上方倾斜），所以供给量和价格是同向变动的。因此，计算出来的供给价格弹性常是一个正数。

供给的区间价格弹性

当价格变化幅度较大时同样使用中点法来计算区间弹性，以保证结果的一致性。
供给的区间价格弹性 = 供给量变化除以平均供给量 / 价格变化除以平均价格 供给的区间价格弹性 = 供给量变化除以平均供给量 / 价格变化除以平均价格 供给的区间价格弹性=供给量变化除以平均供给量/价格变化除以平均价格

影响供给价格弹性的因素

• 生产技术（和生产周期）内在逻辑 ：生产商品的技术复杂性、周期的长短，以及改变产量的难易程度，直接决定了供给弹性的大小。
  • 举例 ：
    • 低弹性：如农产品（像水果、粮食）。如果市场上苹果价格突然上涨，果农没有办法立刻变出更多的苹果来供应。因为苹果树的生长需要很长的时间，产量在短期内是固定的。同样，像一些需要复杂工艺和长生产线的工业品（比如芯片），其短期内的供给弹性也较低。
    • 高弹性：如一些技术简单、容易扩大生产的商品（像T恤衫）。如果T恤衫价格上涨，服装厂可以很容易地增加工人的班次、开启闲置的生产线，迅速增加产量来响应价格变化。
• 时间范围内在逻辑 ：影响供给弹性最重要的因素。时间越长，生产者调整生产规模的灵活性就越大，供给弹性也就越大。
  • 短期内：工厂的规模、机器的数量等都是固定的。面对价格上涨，企业只能通过让工人加班等方式有限地增加产量。因此，短期供给弹性通常较小。
  • 长期内：企业有充足的时间来建设新的厂房、购买新的机器、雇佣更多的工人，甚至可以改进生产技术。因此，长期供给弹性要远大于短期。
• 市场进入与退出内在逻辑 ：这个因素本质上是时间范围在整个市场层面的体现，主要影响长期供给弹性。
  • 举例：如果某个行业的产品价格持续上涨且利润丰厚，长期来看，就会吸引新的企业进入这个市场。新企业的加入会大大增加整个市场的总供给量。反之，如果价格持续低迷导致亏损，一些现有企业可能会选择退出市场，从而减少总供给。这种企业的自由进入和退出，使得市场的长期供给曲线非常有弹性。

供给曲线形状与价格弹性

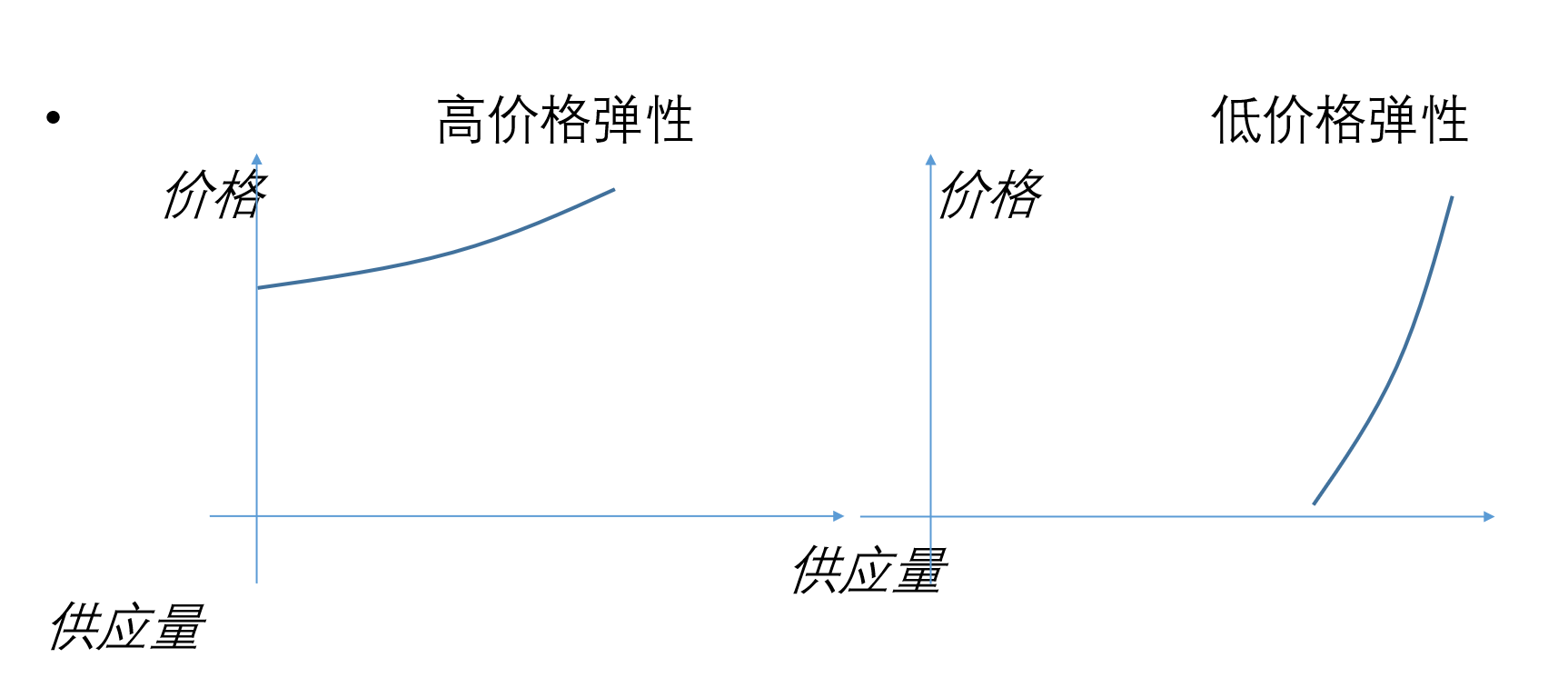
高价格弹性的供给曲线（左图）：

• 形状特征：曲线的形态相对平坦。
• 经济学含义：价格（纵坐标）只要有小幅的上涨，生产者就会大幅增加他们的产量，使得供给量（横坐标）向右延伸很长一段距离。说明生产者的供给能力很强，调整产量的空间很大。
• 结论：价格的微小变化能引起供给量的巨大变化，说明生产者对价格信号的反应非常灵敏。因此，一条相对平坦的供给曲线，代表了高价格弹性，通常对应于那些生产技术简单、容易扩大产能的商品，或者是在一个较长的时间范围内。

低价格弹性的供给曲线（右图）：

• 形状特征：曲线的形态相对陡峭。
• 经济学含义：即使价格（纵坐标）上涨了很高的幅度，生产者的供给量（横坐标）也只能增加一点。这往往意味着生产者的产能已经接近极限，或者受到了技术、资源、生产周期等因素的严格限制。
• 结论：价格的巨大变化只能引起供给量的微小变化，说明生产者的供给能力受到了很大限制，无法对价格变化做出迅速和充分的反应。因此，一条相对陡峭的供给曲线，代表了低价格弹性。这种情况常见于生产周期长（如农产品）、资源稀缺（如稀有矿产）或者短期内产能固定的行业。

从弹性角度观察市场变化（应用案例）

气候与农民收入（谷贱伤农现象）：

• 观察到的现象：风调雨顺的年份，农作物大丰收，但农民的总收入反而可能下降了。
• 弹性角度的解释：粮食这类基础农产品的需求是缺乏弹性的。因为粮食是生活必需品，每个人每天的饭量是基本固定的。粮价贵了，人们也还是要硬着头皮买，因为不吃不行。
• 逻辑推演：大丰收意味着市场上粮食的供给大幅增加（供给曲线向右移动）。由于需求曲线非常陡峭（缺乏弹性），为了把这些新增的粮食都卖出去，价格必须大幅度下降。结果就是，价格下降的百分比，远远超过了销量增加的百分比。对于缺乏弹性的商品，降价会导致总收入下降。因此，出现了丰收反而歉收的奇怪结果。

猪周期、猪瘟与养殖户收入：

• 观察到的现象：前些年爆发非洲猪瘟后大量生猪死亡，导致猪肉价格飞涨。对于那些幸存下来、还有猪可卖的养殖户来说，他们的收入是增加了还是减少了？
• 弹性角度的解释：猪肉的需求也是缺乏弹性的，因为猪肉是中国居民最重要的肉类消费品，消费习惯很稳定，短期内很难找到完美的替代品。因此，即使价格上涨，大部分家庭还是会继续购买，只是可能少买一点。
• 逻辑推演：猪瘟导致生猪供给大幅减少（供给曲线向左移动）。由于需求曲线非常陡峭（缺乏弹性），市场上供给的少量减少，价格大幅度上涨。对于那些还有猪可卖的养殖户来说，他们卖出的猪的数量虽然可能和往年一样甚至更少，但每头猪的价格上涨的幅度惊人。价格上涨的百分比，远远超过了他们可能面临的销量的稳定甚至微弱下降。根据总收入法则，对于缺乏弹性的商品，涨价会导致总收入增加。因此，幸存的养殖户在这期间获得了非常高的利润。

互联网平台常提供免费但有用的服务：

• 观察到的现象：搜索引擎、社交媒体、邮箱等等，这些每天都在用的、非常有价值的服务，为什么都是免费的？公司如何盈利？
• 弹性角度的解释：涉及到交叉价格弹性的概念，以及双边市场的商业模式。
• 逻辑推演：平台提供给用户的核心服务（如搜索）是免费的。这可以看作是一种策略，利用极高的价格弹性（价格从一个很小的正数降到零，需求量会激增到数以亿计），来最大限度地吸引用户，建立一个巨大的用户流量池。这个核心服务和用户的"注意力"或"数据"是"互补品"。用户使用免费搜索，就必然"搭配"着贡献了他的注意力和搜索数据。平台真正的客户不是我们这些普通用户，而是另一边的广告商。平台将用户的注意力/数据这个"商品"卖给广告商。因此，免费的核心服务，是为了生产出有价值的互补品（注意力），再将这个互补品卖给第三方来盈利。这是一种典型的"羊毛出在猪身上"的模式。

医疗服务的需求弹性与医疗体制：

• 观察到的现象：几乎所有国家政府都会深度介入医疗领域，而不会让其完全市场化。为什么？
• 弹性角度的解释：医疗服务的需求是极端缺乏弹性的，因为健康和生命是无价的。当一个人面临生命危险时，他对救命药品和服务的需求，几乎不会因为价格高低而改变。我们不会因为手术"打折"就去做一个，也不会因为急救费用高昂就选择放弃。
• 逻辑推演：如果将这样一个需求极端缺乏弹性的领域完全交给市场，供给方（医院、药厂）会发现，他们可以非常大地提高价格，而需求量（病人数量）几乎不会减少。这将导致他们的收入急剧增加。这种逐利行为会把价格推高到普通人完全无法承受的水平，最终导致只有富人才能看得起病，造成严重的社会不公平和人道主义危机。
• 结论：正是因为医疗服务需求极端缺乏弹性，纯粹的市场机制会在此处失灵。因此，政府必须通过医保、价格管制、公立医院等方式进行干预，以保证医疗的公益性和可及性。