0012机器学习KNN算法

0012机器学习KNN算法

• 一、KNN算法原理
• 二、KNN三要素
• 三、python代码理解KNN算法
• 四、KD树(kd_tree)
• [五、球树(Ball Tree)](#五、球树(Ball Tree))
• 六、API调用
• • [1.1 基于鸢尾花数据的KNN案例](#1.1 基于鸢尾花数据的KNN案例)
  • [2.2 KNNImputer缺失值填充](#2.2 KNNImputer缺失值填充)
  • [3.3 基于KNN的数据下采样方法](#3.3 基于KNN的数据下采样方法)

一、KNN算法原理

• K近邻(K-nearest neighbors,KNN)是一种基本的机器学习算法，所谓k近邻，就是k个最近的邻居的意思，说的是每个样本都可以用它最接近的k个邻居来代表。比如：判断一个人的人品，只需要观察与他来往最密切的几个人的人品好坏就可以得出，即"近朱者赤，近墨者黑"；KNN算法既可以应用于分类应用中，也可以应用在回归应用中。
• KNN在做回归和分类的主要区别在于最后做预测的时候的决策方式不同。KNN在分类预测时，一般采用多数表决法；而在做回归预测时，一般采用平均值法。
  
  
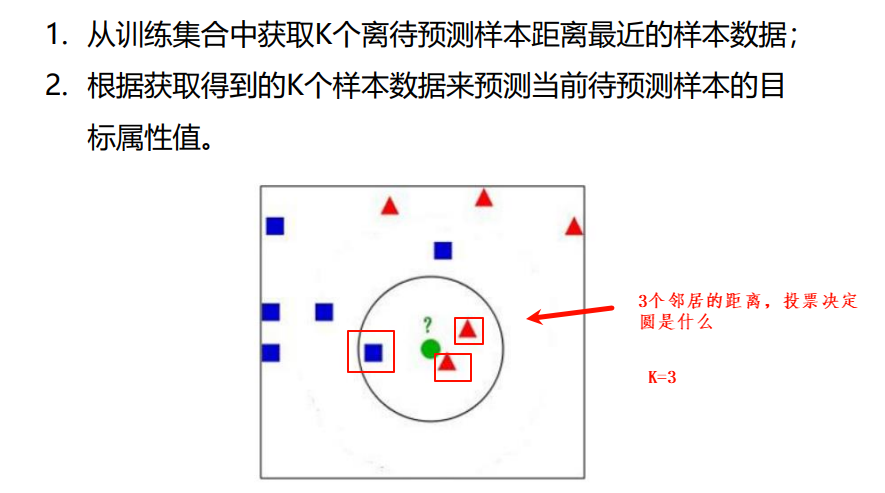
• KNN算法一般用欧氏距离求

二、KNN三要素

在KNN算法中，非常重要的主要是三个因素：

• K值的选择：对于K值的选择，一般根据样本分布选择一个较小的值，然后通 过交叉验证来选择一个比较合适的最终值；当选择比较小的K值的时候， 表示使用较小领域中的样本进行预测，训练误差会减小，但是会导致模型变得 复杂，容易过拟合；当选择较大的K值的时候，表示使用较大领域中的样本进行预测，训练误差会增大，同时会使模型变得简单，容易导致欠拟合；
• 距离的度量：一般使用欧氏距离；
• 决策规则：在分类模型中，主要使用多数表决法或者加权多数表决法；在回 归模型中，主要使用平均值法或者加权平均值法。

  • KNN分类预测规则

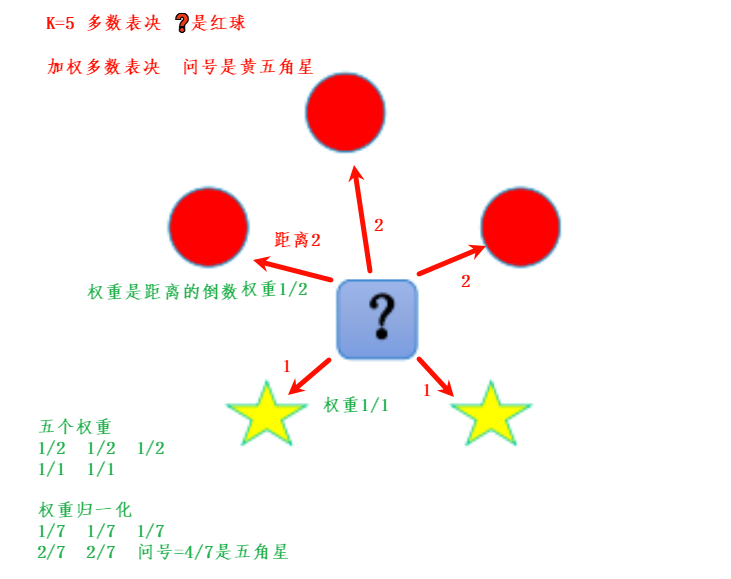
    • 多数表决法：每个邻近样本的权重是一样的，也就是说最终预测的结果为出现类别最多的那个类
    • 加权多数表决法：每个邻近样本的权重是不一样的，一般情况下采用权重和距离成反比的方式来计算，也就是说最终预测结果是出现权重最大的那个类别；
    • 

  • KNN回归预测规则

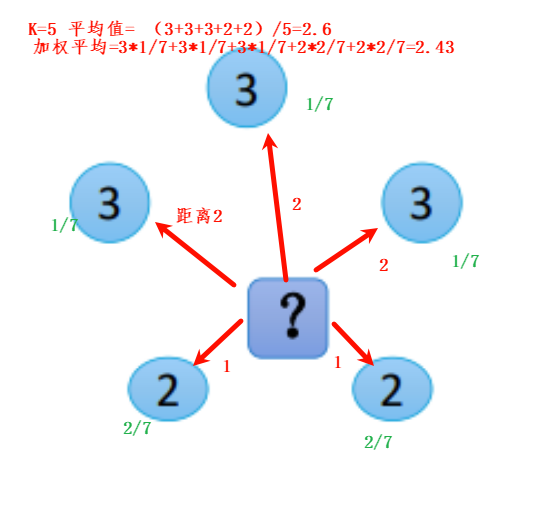
    • 平均值法：每个邻近样本的权重是一样的，也就是说最终预测的结果为所有邻近样本的目标属性值的均值；
    • 加权平均值法：每个邻近样本的权重是不一样的，一般情况下 采用权重和距离成反比的方式来计算，也就是说在计算均值的时候进行加权操作；
    • 

三、python代码理解KNN算法

'''
简单实现一下等权分类 封装成KNN类
    实现fit，predict，score方法
'''
import sys
import numpy as np
import pandas as pd
class KNN:
    '''
    KNN的步骤：
    1、从训练集合中获取K个离待预测样本距离最近的样本数据；
    2、根据获取得到的K个样本数据来预测当前待预测样本的目标属性值
    '''
    def __init__(self, k):
        self.k = k
        pass
    def fit(self, x, y):
        '''
        训练模型  实际上就是存储数据
        :param x: 训练数据x
        :param y: 训练数据y
        :return:
        '''
        ### 将数据转化为numpy数组的形式进行存储
        self.train_x = np.array(x)
        self.train_y = np.array(y)
    def feach_k_neighbors(self, x):
        '''
        # 1、从训练集合中获取K个离待预测样本距离最近的样本数据；
        # 2、根据获取得到的K个样本数据来预测当前待预测样本的目标属性值
        :param x:待预测的一条数据
        :return: 最近k个邻居的label
        '''
        ###列表 [[dis1，标签1]，[dis2，标签2].。。。。。。]
        listdistance = []
        ##循环每一个数据，计算他的dis
        for index, i in enumerate(self.train_x):
            # print(index)
            dis = np.sum((np.array(i) - np.array(x)) ** 2) ** 0.5  # 求差值的平方和再开方（求欧氏距离）
            listdistance.append([dis, self.train_y[index]])
        # print(listdistance)
        ##按照dis从小到大进行排序
        listdistance.sort()
        # print(listdistance)
        # sys.exit()
        ##选取K个邻居放入投票箱
        # print(listdistance[:self.k])
        arr = np.array(listdistance[:self.k])[:, -1]
        # print(arr)
        return arr
    def predict(self, x):
        '''
        对待预测数据进行预测
        :param x: 待预测数据的特征属性x 是个矩阵
        :return: 所有数据的预测label
        '''
        ### 将数据转化为numpy数组的形式
        self.pre_x = np.array(x)
        # 遍历每一条带预测数据
        Y_pre = []
        for x in self.pre_x:
            # print(x)
            # 1、从训练集合中获取K个离待预测样本距离最近的样本数据；
            k_nearst_neighbors_label = self.feach_k_neighbors(x)

            # 2、根据获取得到的K个样本数据来预测当前待预测样本的目标属性值
            ##统计投票
            a = pd.Series(k_nearst_neighbors_label).value_counts()
            # print(a)
            # pre = a.idxmax()  ##idxmax() 和 argmax 功能一样，获取最大值对应的下标索引
            y_pre = a.idxmax()
            # pre = a.argmax()
            # print(pre)
            Y_pre.append(y_pre)
        return Y_pre
    def score(self, x, y):
        '''
        准确率
        :param x:
        :param y:
        :return: 准确率
        '''
        y_hat = self.predict(x)
        acc = np.mean(y == y_hat)
        return acc
def movie():
    T = np.array([
        [3, 104, -1],
        [2, 100, -1],
        [1, 81, -1],
        [101, 10, 1],
        [99, 5, 1],
        [98, 2, 1]])
    X_train = T[:, :-1]
    Y_train = T[:, -1]
    x_test = [[18, 90], [50, 50]]
    knn = KNN(k=3)
    knn.fit(x=X_train, y=Y_train)
    print('训练集预测结果：{}'.format(knn.predict(X_train)))
    print('训练集得分：{}'.format(knn.score(x=X_train, y=Y_train)))
    # knn.fetch_k_neighbors(x_test[0])
    print('预测结果：{}'.format(knn.predict(x_test)))
def iris():
    from sklearn.datasets import load_iris  # 加载一些数据集
    from sklearn.model_selection import train_test_split

    X, Y = load_iris(return_X_y=True)
    print(X.shape, Y.shape)
    x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.2, random_state=0)
    print(x_train.shape, y_train.shape)
    knn01 = KNN(k=3)
    knn01.fit(x_train, y_train)
    print(knn01.score(x_train, y_train))
    print(knn01.score(x_test, y_test))
if __name__ == '__main__':
    #movie()
    iris()

以上代码是通过蛮力实现(brute)：计算预测样本到所有训练集样本的距离，然后选择最小的k个距离即可得到K个最邻近点。缺点在于当特征数比较多、样本数比较多的时候，算法的执行效率比较低

四、KD树(kd_tree)

当样本数据量少的时候，我们可以使用brute这种暴力的方式进行求解最近邻，即计算到所有样本的距离。但是当样本量比较大的时候，直接计算所有样本的距离，工作量有点大，所以在这种情况下，我们可以使用KD Tree来快速的计算。

KD树采用从m个样本的n维特征中，分别计算n个特征取值的方差，用方差最大的第k维特征nk作为根节点。对于这个特征，选择取值的中位数nkv作为样本的划分点，对于小于该值的样本划分到左子树，对于大于该值的样本划分到右子树，该值为根节点。接下来对左右子树采用同样的方式找方差最大的特征作为根节点，递归即可产生 KD树。

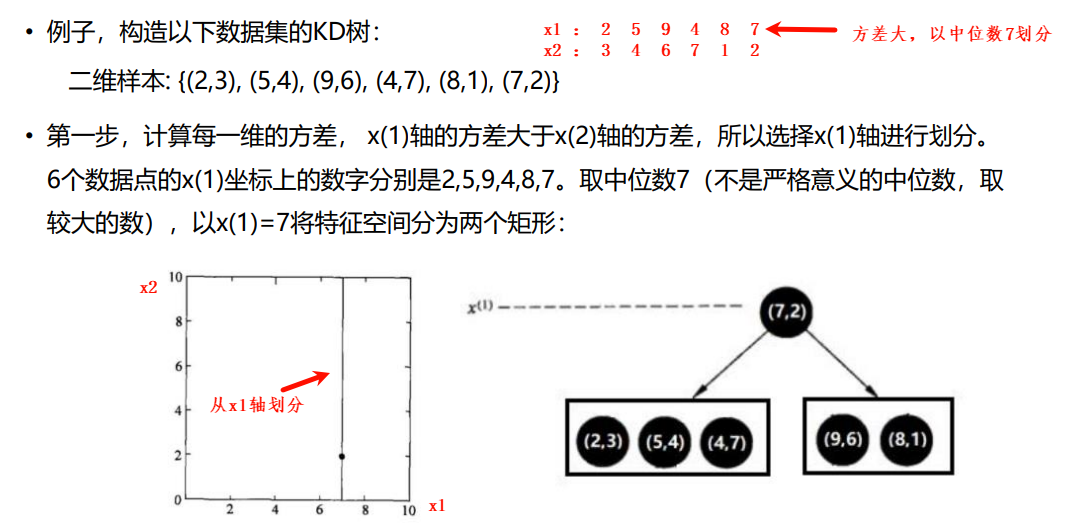
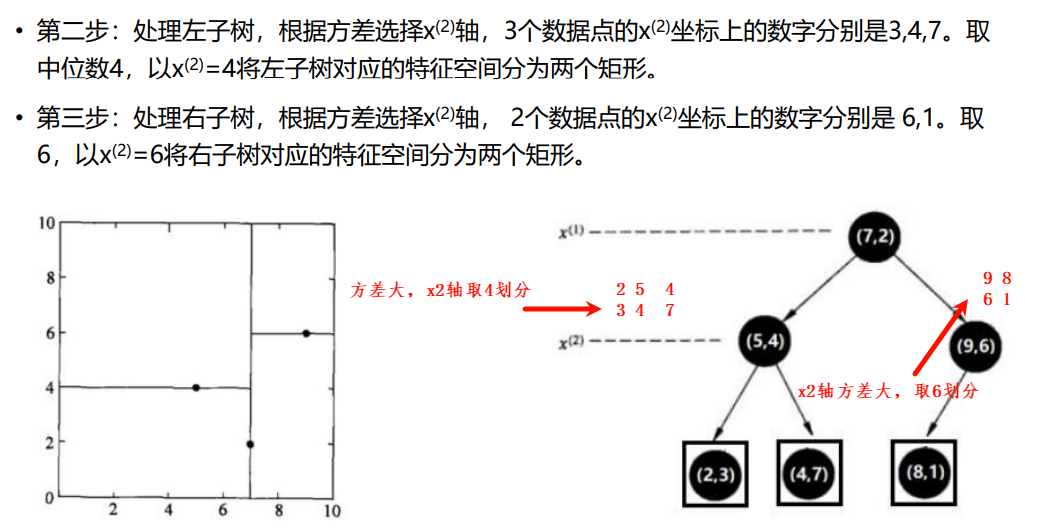
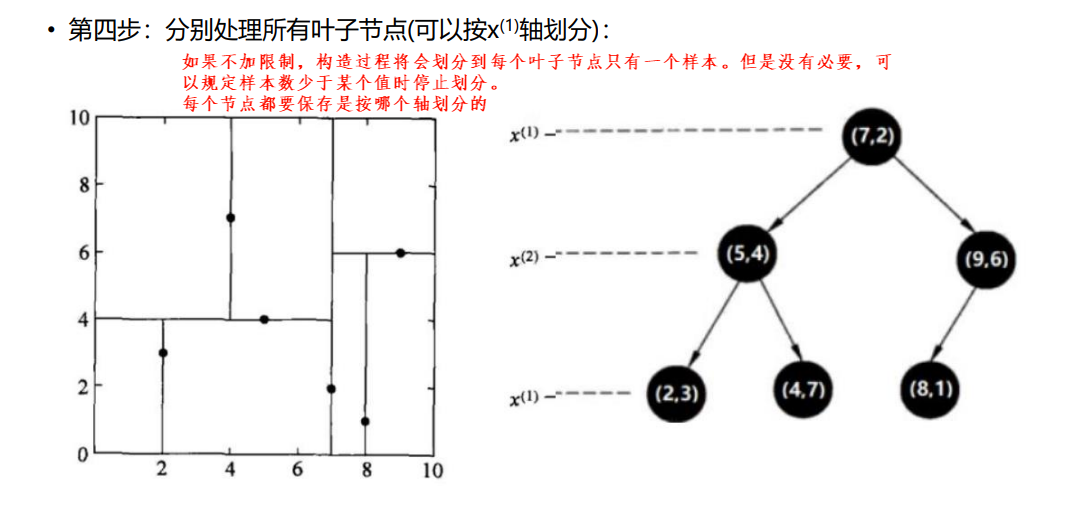
如果来了一个预测样本，可以根据划分后的树，从局部找到k个邻居，不用在全局找

五、球树(Ball Tree)

• 使用kd树最近邻预测时，矩形与超球面易于相交，时常会因为菱角相交导致一些无关多余的搜索，球树就是对kd树的这个缺点进行改进而生，通过将特征点转化为球状分割，从而减少无效相交。
• 球树的构建步骤：
  • 先构建一个超球体，这个超球体是可以包含所有样本的最小球体。
  • 从球中选择一个离球的中心最远的点，然后选择第二个点离第一个点最远，将球中所有的点分配到离这两个聚类中心最近的一个上，然后计算每个聚类的中心，以及聚类能够包含它所有数据点所需的最小半径。这样我们得到了两个子超球体，和KD树里面的左右子树对应。
  • 对于这两个子超球体，递归执行步骤最终得到了一个球树

六、API调用

1.1 基于鸢尾花数据的KNN案例

import pandas as pd
import numpy as np
import sys
from sklearn.model_selection import train_test_split
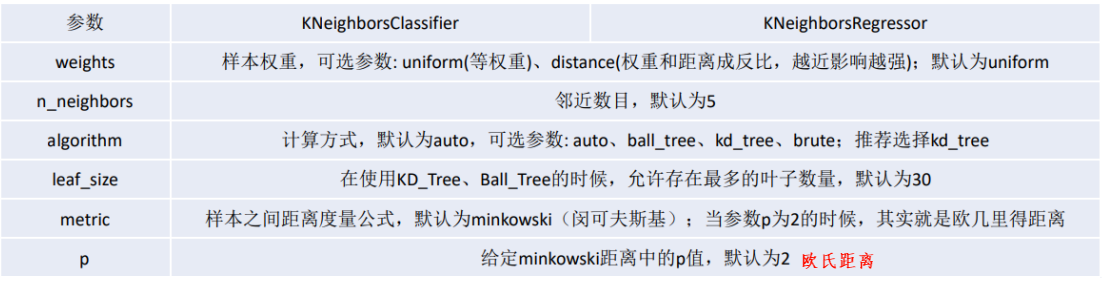
from sklearn.neighbors import KNeighborsClassifier, KNeighborsRegressor
from sklearn.metrics import accuracy_score, recall_score, precision_score, r2_score
from sklearn.preprocessing import LabelEncoder

# 1. 加载数据(数据一般存在于磁盘或者数据库)
path = '../data/iris.data'
names = ['x1', 'x2', 'x3', 'x4', 'y']
df = pd.read_csv(path, header=None, names=names, sep=",")
print(df.head())
print(df.shape)
print(df["y"].value_counts())
# sys.exit()

# 2. 数据清洗
# NOTE: 不需要做数据处理
def parse_record(row):
    result = []
    r = zip(names, row)
    for name, value in r:
        if name == 'y':
            if value == 'Iris-setosa':
                result.append(1)
            elif value == 'Iris-versicolor':
                result.append(2)
            elif value == 'Iris-virginica':
                result.append(3)
            else:
                result.append(0)
        else:
            result.append(value)
    return result


df = df.apply(lambda row: pd.Series(parse_record(row), index=names), axis=1)
df['y'] = df['y'].astype(np.int32)
df.info()
print(df["y"].value_counts())
flag = False
# sys.exit()
# df = df[df.cla != 3]
# print(df.cla.value_counts())

# # 3. 根据需求获取最原始的特征属性矩阵X和目标属性Y
# X = df.iloc[:,:-1]
X = df[names[0:-1]]
print(X.shape)
Y = df[names[-1]]
print(Y.shape)
print(Y.value_counts())
# sys.exit()

# 4. 数据分割
# train_size: 给定划分之后的训练数据的占比是多少，默认0.75
# test_size:
# random_state：给定在数据划分过程中，使用到的随机数种子，默认为None，使用当前的时间戳；给定非None的值，可以保证多次运行的结果是一致的。
x_train, x_test, y_train, y_test = train_test_split(X, Y, train_size=0.8, random_state=1)
print("训练数据X的格式:{}, 以及类型:{}".format(x_train.shape, type(x_train)))
print("测试数据X的格式:{}".format(x_test.shape))
print("训练数据Y的类型:{}".format(type(y_train)))

# 5. 特征工程的操作
# NOTE: 不做特征工程

# 6. 模型对象的构建
"""
KNN:
    n_neighbors=5,
    weights='uniform',
    algorithm='auto', 
    leaf_size=30,
    p=2,
    metric='minkowski', 
    metric_params=None, 
    n_jobs=1
"""
KNN = KNeighborsClassifier(n_neighbors=10, weights='uniform', algorithm='kd_tree')

# 7. 模型的训练
KNN.fit(x_train, y_train)

# 8. 模型效果评估
train_predict = KNN.predict(x_train)
test_predict = KNN.predict(x_test)
print("KNN算法：测试集上的效果(准确率):{}".format(KNN.score(x_test, y_test)))
print("KNN算法：训练集上的效果(准确率):{}".format(KNN.score(x_train, y_train)))
print(accuracy_score(y_true=y_train, y_pred=train_predict))
# 模型的保存与加载
# pip install joblib
import joblib
joblib.dump(KNN, "./knn.m")  # 保存模型
# joblib.load(path) # 加载模型

2.2 KNNImputer缺失值填充

KNNImputer可以更便捷地处理缺失值，并且与直接用均值、中位数相比更为可靠。利用"近朱者赤"的KNN算法原理，这种插补方法借助其他特征的分布来对目标特征进行缺失值填充。

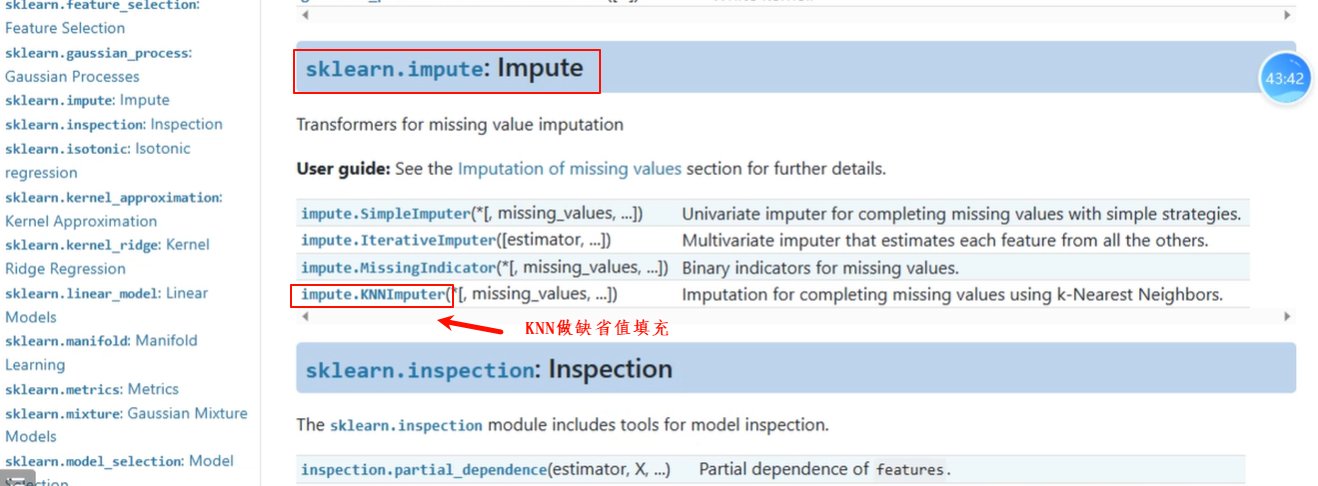
举例1：

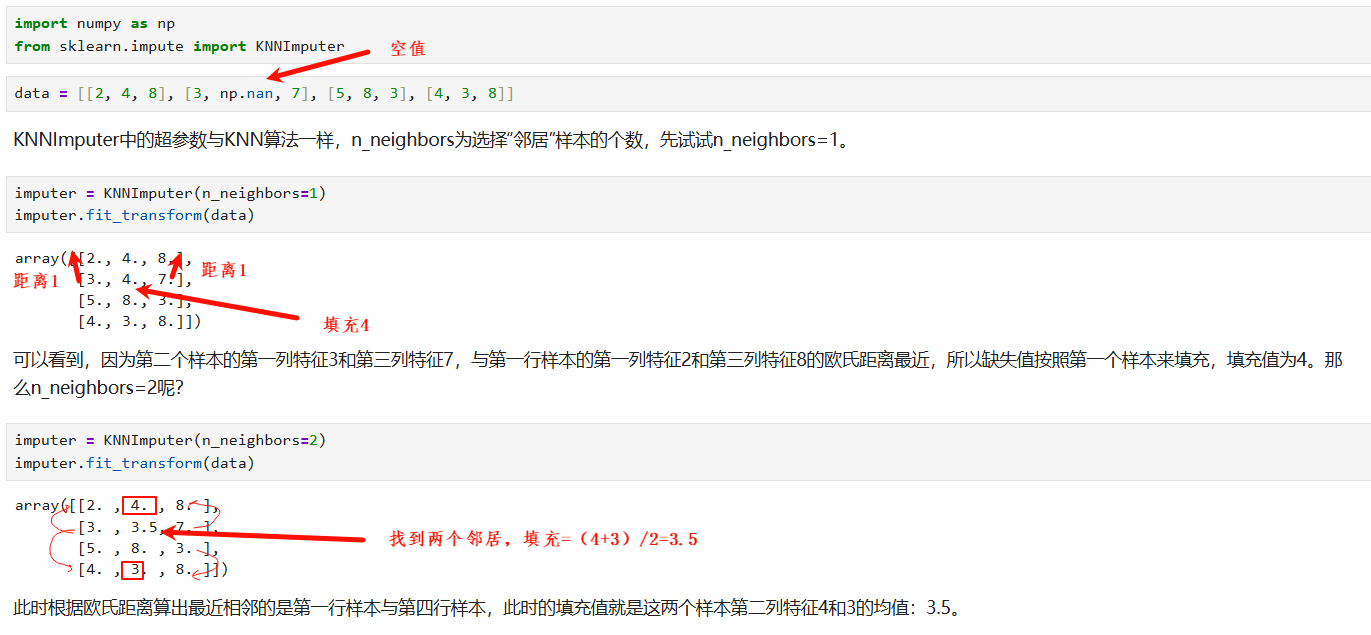
举例2：

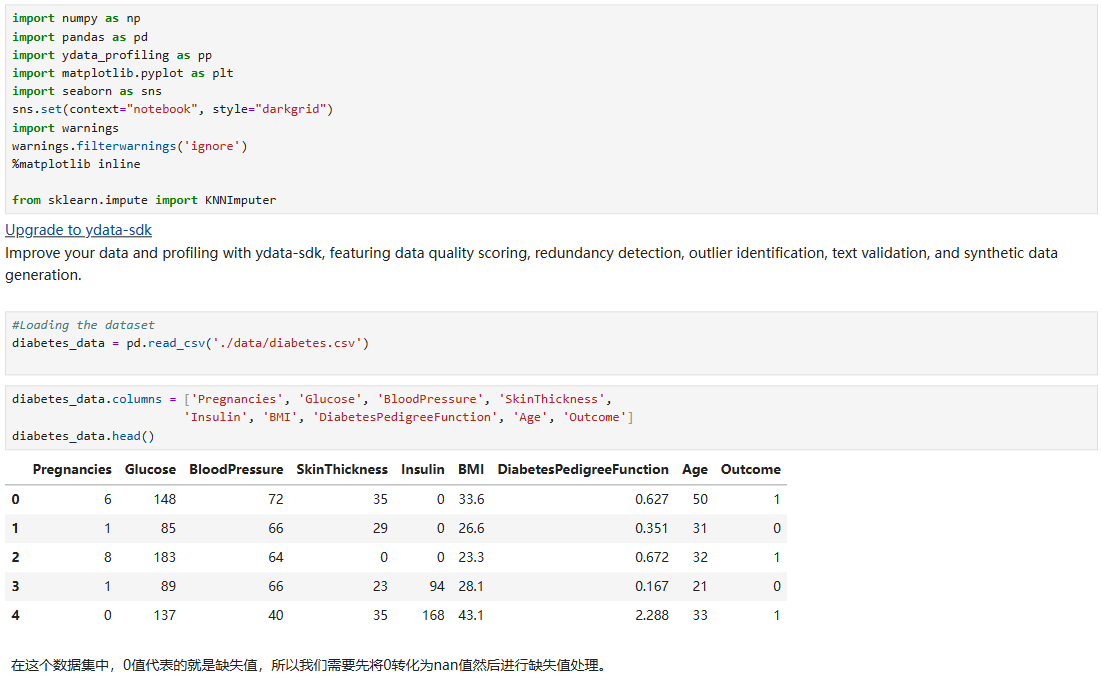
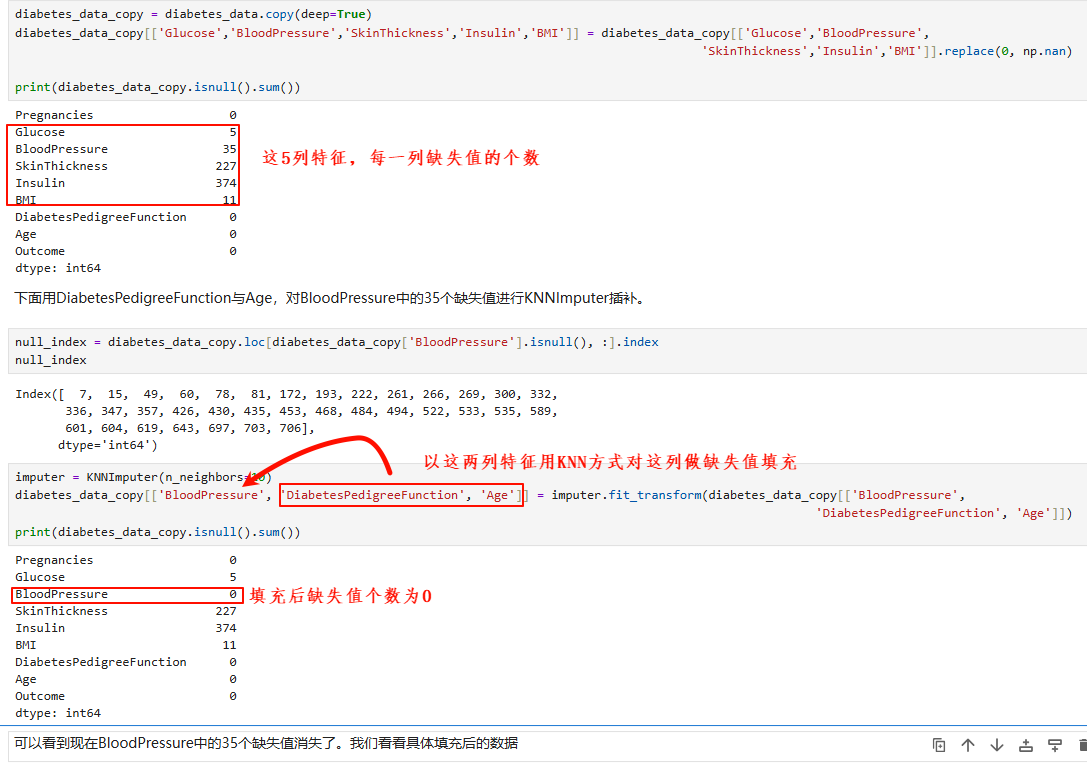
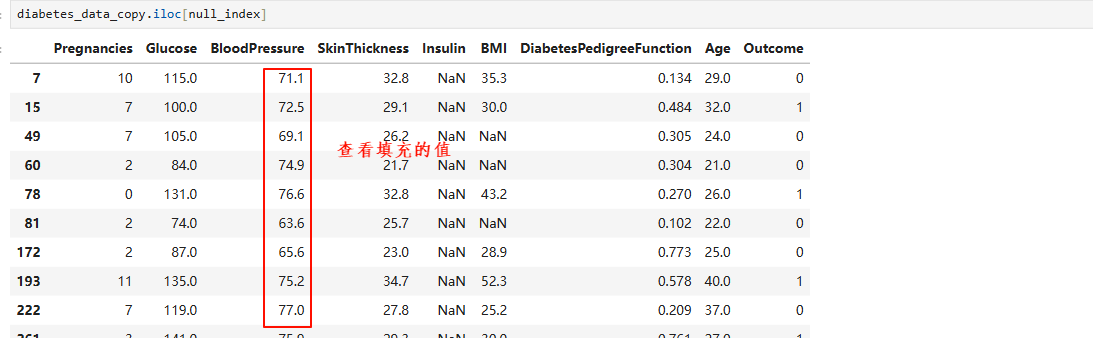
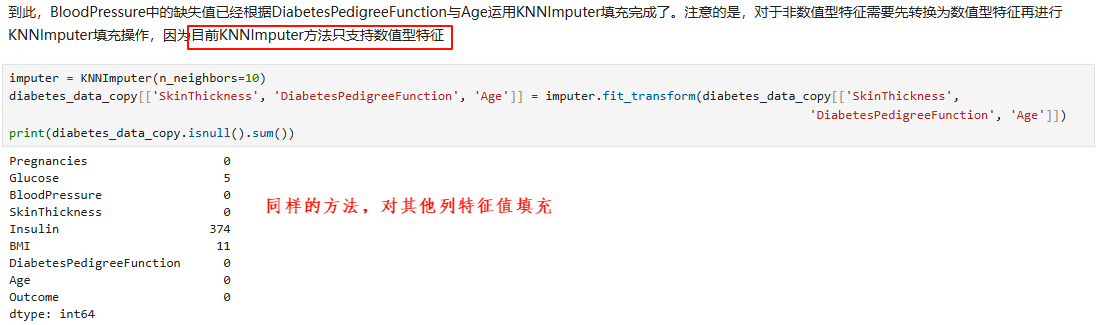
3.3 基于KNN的数据下采样方法

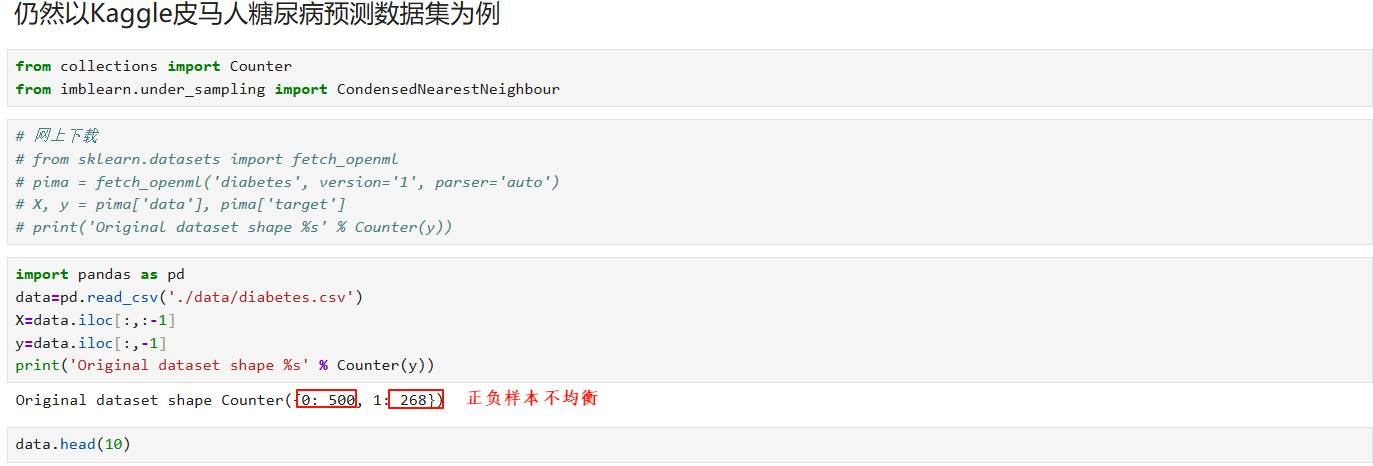
所谓数据下采样，就是减小数据集的样本数量。

• 当样本量太多的时候，为了能够快速学习迭代模型，我们可能会剔除掉训练集中的冗余样本，所谓的冗余样本，就是指对模型的训练效果没有影响或者影响较小的样本，即使剔除后，模型仍能够做到较高的可用性。
• 当数据不均衡的时候，可以使用数据下采样减少样本数量多的那种类型的样本数量(也可以增加样本 数量少的那种类型的样本数量，称为数据上采样。)

1、CNN

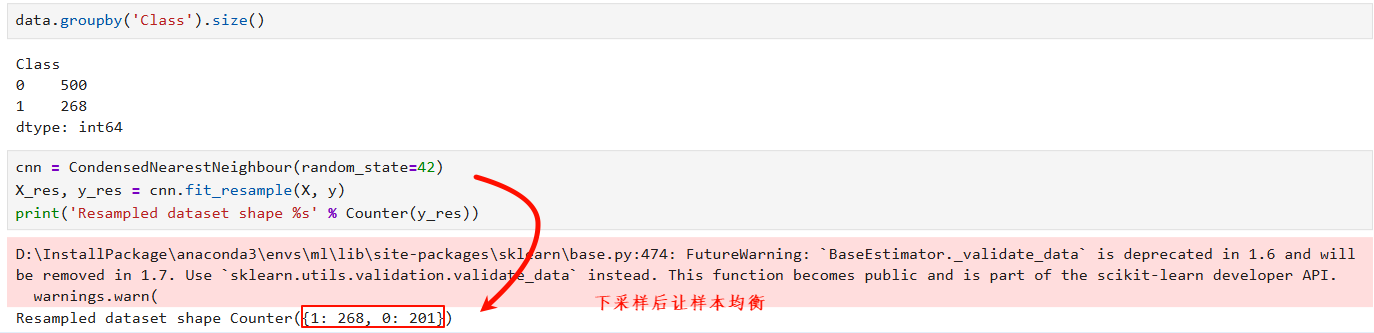
2、ENN