【MySQL】索引 (上) —— 索引的定义与数据结构

[0. 什么是索引](#0. 什么是索引)

[1. 索引应该选择哪种数据结构](#1. 索引应该选择哪种数据结构)

[1.1 哈希表](#1.1 哈希表)

[1.2 二叉搜索树](#1.2 二叉搜索树)

[1. 二叉搜索树的特点与大致结构](#1. 二叉搜索树的特点与大致结构)

[2. 二叉搜索树的缺点](#2. 二叉搜索树的缺点)

[3. 为什么一次磁盘I/O只能读取二叉搜索树的一个节点？](#3. 为什么一次磁盘I/O只能读取二叉搜索树的一个节点？)

[1.3 B树（多路搜索树）](#1.3 B树（多路搜索树）)

[1. B树的特点](#1. B树的特点)

[2. B树的大致结构](#2. B树的大致结构)

[3. B树的缺点](#3. B树的缺点)

[1.4 B+树](#1.4 B+树)

[1. B+树的特点与大致结构](#1. B+树的特点与大致结构)

[2. 索引键上提为路由键](#2. 索引键上提为路由键)

[3. B+树的优势](#3. B+树的优势)

[#1# 各数据结构作为索引的功能和效率比较](#1# 各数据结构作为索引的功能和效率比较)

[2. MySQL中的页](#2. MySQL中的页)

[2.1 页的大小、以及为何是这么大](#2.1 页的大小、以及为何是这么大)

[2.2 页在B+树中的结构](#2.2 页在B+树中的结构)

a.页头、页尾、数据行

b.页主体

c.页目录

[#2# 总结页结构的异同](#2# 总结页结构的异同)

0. 什么是索引

MySQL中的索引 ，是一种帮助数据库高效获取数据的、排好序的快速查找数据结构。它相当于数据库表的"目录"。

索引不是对原表的完全拷贝再排序，而是会截取关键字段组成一个查询用的"目录"。

MySQL索引类似于书籍的目录，比如汉语字典的目录页，我们可以按笔画、偏旁部首、拼音等排序的目录（索引）快速查找到需要的字。

类比	《新华字典》	MySQL 数据库表
完整数据	正文：按拼音排序的所有汉字和解释。	数据表：存储所有数据的物理文件（如 `user` 表，包含 id, name, email 等）。
查找需求	根据"字形"（部首/笔画）查找字的读音和意思。	根据某个"字段值"查找数据行（如 `WHERE name = '张三'`）。
索引载体	《部首检字表》：一个独立的部分，按"部首+笔画"排序。	索引文件：一个独立的数据结构（通常是 B+树），存储了索引字段的值和对应数据行的物理地址。
查找过程	1. 查《检字表》找到页码。 2. 根据页码翻到正文。	1. 在索引树中找到对应的值，获得数据行地址（如主键ID或磁盘指针）。 2. 根据地址定位到数据行所在位置并读取。
效率提升	避免了从第一页开始逐页扫描整本字典。	避免了逐行扫描整个数据表（全表扫描）。

新华字典中所采用的索引方式不止一种，常见的目录有两种，一种是按"部首+笔画"排序的部首检字表 ，一种是按"拼音+音节"排序的拼音检字表：

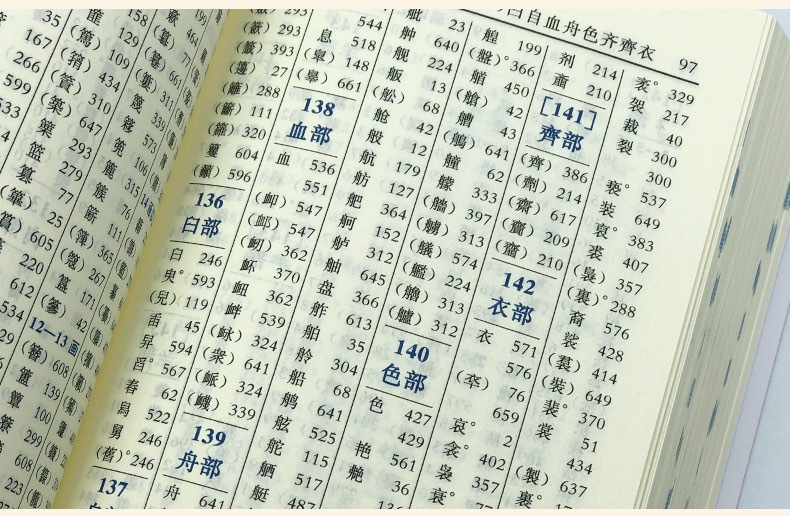
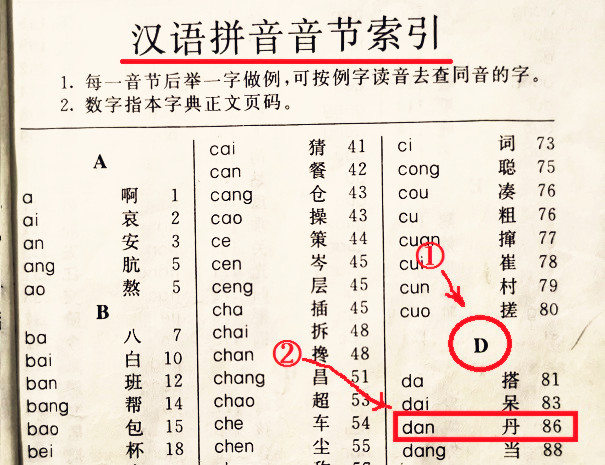
同样的，MySQL中的索引种类也不止一种，例如主键索引、唯一索引......

1. 索引应该选择哪种数据结构

使⽤索引的⽬的只有⼀个，就是提升数据检索的效率，既然这样我们应该使用什么样的数据结构来实现索引呢？

1.1 哈希表

弊端：

虽然哈希表的时间复杂度可以达到惊人的O(1)，但是它并不适合用作索引，最大弊端在于哈希表不支持范围查找。

例如要查找分数 score < 80 的数据，分数是没有负值的，所以查找的范围是[0, 80)。数学上该区间是连续的 ，但是在数据库中这段区间是由一个个离散的数据组成。

假如使用哈希表作为索引的数据结构，由于存储的数值是离散分布的，存储值通过哈希函数计算出来的哈希值（地址）又是唯一，这就导致了哈希值(存储的地址)也是离散的。这就是哈希表的离散映射。

再者，哈希函数不是线性的，它是伪随机函数。那很可能会存在第2个存储值查找出来的存储地址比第1个存储地址低出很多，而第3个存储值查找出来的地址比第1个存储地址高出很多的情况。

也就是说，原本一段线性且连续的存储值查找范围，经过哈希离散映射后找到的存储地址是随机且离散的。

1.2 二叉搜索树

1. 二叉搜索树的特点与大致结构

⼆叉搜索树的中序遍历是⼀个有序数组，假如使用二叉搜索树作为索引，大致结构如下：

【**key：**是排序用的数值，截取自真实表中的关键字段】

【**ptr：**是指针，用来指向真实表中的完整数据】

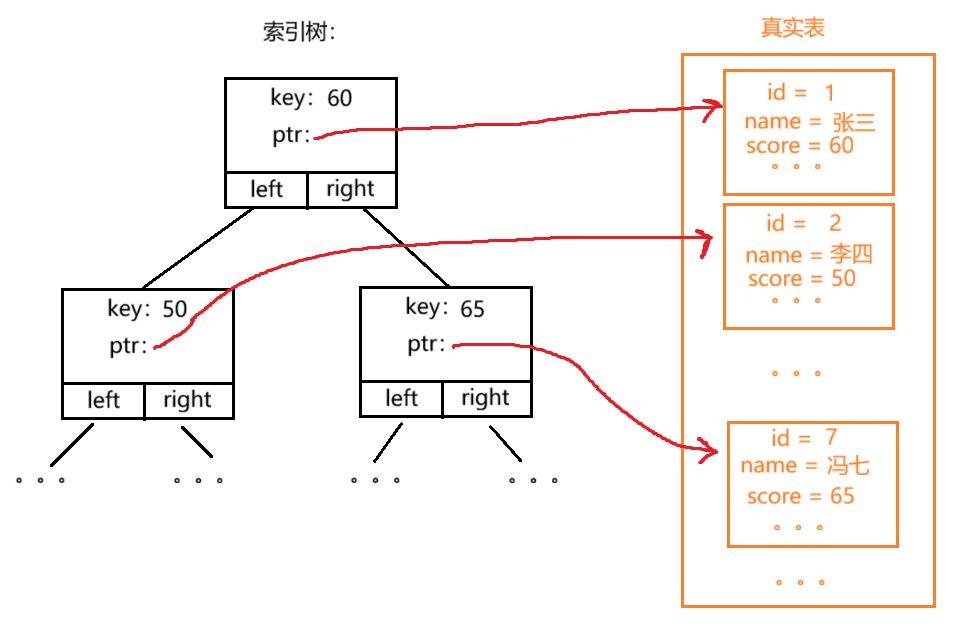
二叉搜索树按中序遍历的话是完全有序的，下面的树按中序遍历的结果是：30 40 45 50 60 65 70 80 90 95。

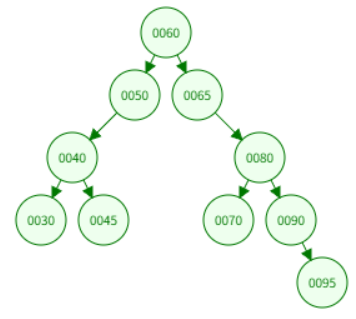
通过栈模拟递归的方式就可以完成中序遍历。如果要范围查找，只需要先在二叉搜索树种找到搜索区间的最小值 （比较的同时会记录父节点），该过程的时间复杂度是O(logN) ，然后从该节点开始进行中序遍历 ，直到找到或越过搜索区间的最大值 后进行剪枝即可。

2. 二叉搜索树的缺点

虽然二叉搜索树可以完成范围查找，但是因为以下几个缺点导致它不能成为索引的数据结构。

弊端：

退化风险： 当数据按顺序插入时，二叉树会退化成链表；时间复杂度也会从O(logN)退化成O(N)。

平衡维护成本高： 使用AVL树或红黑树可以使得搜索树++近似于平衡二叉树，解决了退化风险的问题++ 。在真实表中进行插入删除操作后，在索引中也要同步插入删除，但是AVL树、红黑树的插入删除操作 非常消耗性能，这导致了索引的维护成本也是极高的。

磁盘I/O灾难、树高控制难： 因为二叉树中每个节点最多只有两个节点，当数据量很大时，二叉搜索树的树高也会很高。不幸的是一次磁盘I/O只能读取1个节点，树越高意味着要进行更多次的磁盘I/O。【该缺点是相对多叉树来说的，多叉树由于可以有多个节点所以可以有效控制树高。】

3. 为什么一次磁盘I/O只能读取二叉搜索树的一个节点？

一次I/O只能读取4KB 的内容，而一块硬盘通常能有 256 GB、512 GB 甚至 1 TB，存储量至少是读取量的 65536 倍了。

一个二叉搜索树的节点大约是 24 ~ 40 B，虽然理论上一次I/O能读取多个节点，但是节点在磁盘上随机分布的，再加上磁盘实在是太大了，所以一次I/O基本上只能读1个节点。

1.3 B树（多路搜索树）

1. B树的特点

B树是一种自平衡的多路搜索树，专门为磁盘等外部存储设备设计。它通过保持树的平衡和增加每个节点的分支数量来最小化磁盘I/O次数。

B树的核心特点：

每个节点可以有多个子节点 ，使得树高能保持在比较低的水平，深度优先遍历的时间复杂度永远是O(logN)。 【有效解决了树高控制的问题】

B树的节点增删采用的是分裂/合并 ，其核心主要是内存复制 。【AVL树的节点增删采用旋转的方式，涉及指针重定向，需要改变多个节点的父子关系。B树的特点有效解决了平衡维护的成本问题】

B树的节点大小通常被设计为磁盘页的大小 ，所以一次磁盘I/O只能读取B树中的一个节点。

B树的所有节点（包括内部节点）都可以存储数据。

2. B树的大致结构

一颗4阶B树可以是下面这样：

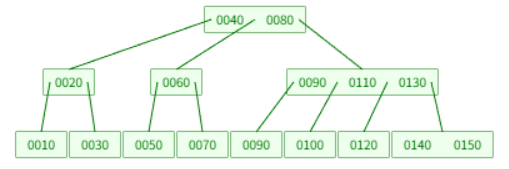
4阶意味着该树的每一个节点最多可以有4个子节点，一个节点内部最多可以有3个key和3个ptr指针，根据3个key值可以分成4个区间范围：

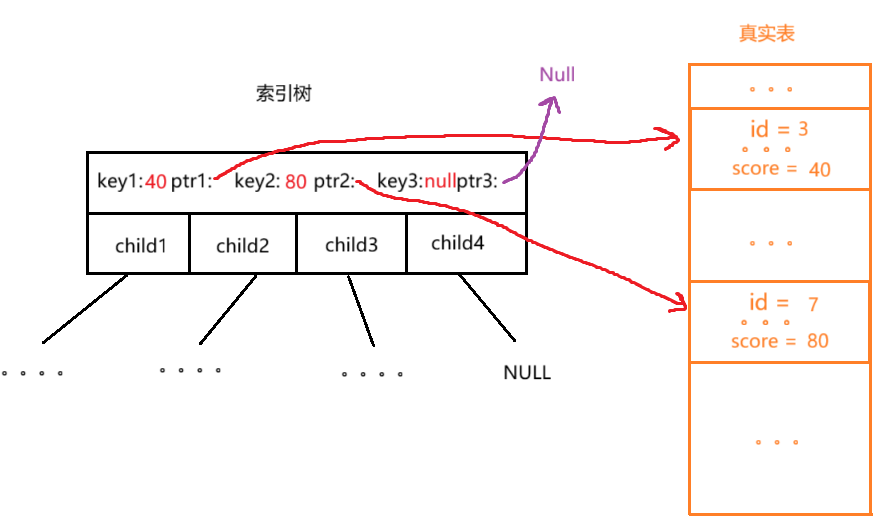
如果静态实现key和ptr的存储，那么会用2个固定大小的数组keys、ptrs。

如果动态实现key和ptr的存储，那么会用2个指针*keys、*ptrs。

3. B树的缺点

B树与B+树相比还是很很多缺点，其中最大的缺点是查询性能的稳定性很差。因为B树中无论是叶子节点还是非叶子，它们都会存储数据。

单值查询时，如 " SELECT * FROM users WHERE id = 25 " 可能在根节点找到，++只需1次++ I/O；" SELECT * FROM users WHERE id = 150 "可能在叶子节点找到，++需要3-4次++I/O

1.4 B+树

1. B+树的特点与大致结构

MySQL的索引使用的就是B+树

B+树是一种多路平衡搜索树，也是B树的优化变种，专为数据库 和文件系统设计。

下图是4阶B+树的演示：

10 ~ 140：

10 ~ 170：

B+树的特点：

所有实际数据（keys 和 ptrs）只存储在叶子节点。

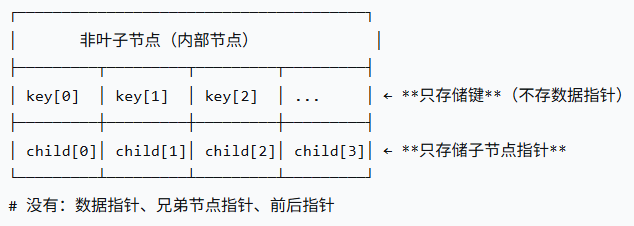
非叶子节点只存储键（keys）和指向子节点的指针，不存储实际数据。

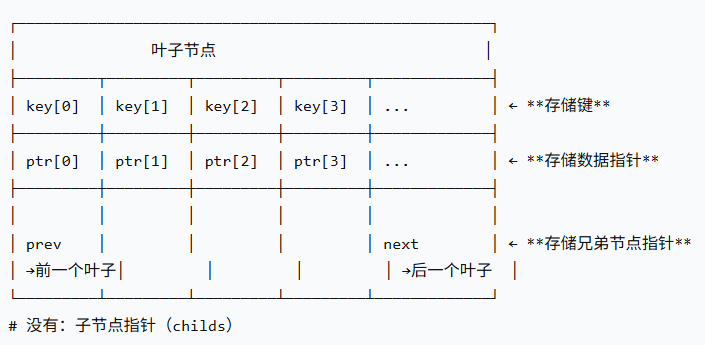
叶子节点通过指针形成有序链表 。MySQL实现的B+树，它的叶子节点使用的是双向链表。

叶子节点与非叶子节点不单只是存储的东西不同，两者的内部结构也不同：

以下是简略图（以4阶B+树为例）：

非叶子节点

（keys、childs）

叶子节点

（keys、ptrs、next和prev）

2. 索引键上提为路由键

内部节点的keys取自叶子节点，用来给子节点划分区间。分裂时，会把子节点中的某个值上提，上提演示如下：（以6阶B+树为例）

叶子节点的分裂：

分裂前：

keys为[10, 20, 30, 40, 50]

插入值为60的key。

6阶B+树最多能有5个key ，现在存在6个key，需要分裂出新的叶子节点。

分裂后：

左兄弟: [10, 20, 25]

右兄弟: [30, 40, 50]

【左兄弟的最大值一定小于右兄弟的最小值 ，所以把右节点的第一个键 = 30上提到父节点的键。】
内部节点的分裂：

分裂前：

keys为[10, 20, 30, 40, 50]

对应的6个子节点： A（对应范围[0, 10)）,B（对应范围[10, 20)）,C（对应范围[20, 30)）,D（对应范围[30, 40)）,E（对应范围[40, 50)）,F（对应范围[50, +∞)）

叶子节点插入的数据足够多，以至于该内部节点的下层需要多加一个子节点G。

6阶B+树最多能有6个子节点 ，现在存在7个子节点，需要分裂出新的内部节点。

子节点 G 对应范围[60, +∞)。

子节点 F 对应的范围变成[50, 60)。

3.分裂后：

左节点: [10,20] 指向子节点A,B,C。

右节点: [40,50] 指向子节点D,E,F。

新节点: [ X ] 指向子节点G。

【左节点有2个key，可以管理前3个旧的子节点(A,B,C)；右节点有2个key，也可以管理后3个旧的子节点(D,E,F)；所以总共4个key 就能管理原本6个旧的子节点，而一开始是有5个key的 ，多出来的那个key就是要上提的key。所以把原节点的中间键 = 30上提到父节点的键。】

从中我们可以总结出2条上提键的规则：

分裂前，原节点的中间键。
分裂后，右节点的第一个键。

3. B+树的优势

树高最小化： B+树是多路平衡树，能够有效控制树高。

范围查找效率高： B+树的叶子节点通过指针形成有序链表，进行范围查询时只需先定位到起始键值的叶子节点，然后沿着链表顺序遍历即可。

查询性能稳：所有实际数据都存储在叶子节点 ，任何查询（无论是等值查询还是范围查询）都必须到达叶子节点才能获取数据。这意味着所有查询的路径长度相同，性能稳定在O(logₘn)级别。

更高的空间利用率： B+树的内部节点不存储数据指针 ，只存储键值和子指针，结构极其紧凑。同样大小的节点，B+树能比B树++多存储约50%的键值++。

支持高效的排序和分组操作： B+树的叶子节点天然就是有序的，数据库可以直接利用这种有序性，避免额外的排序操作，显著提升ORDER BY和GROUP BY查询的性能。

#1# 各数据结构作为索引的功能和效率比较

比较维度	哈希表	二叉搜索树(BST)	B树	B+树
范围查询	不支持或效率低需要扫描整个表	支持但效率一般中序遍历O(n)	支持需要中序遍历的节点更少	高效支持叶子节点链表顺序访问
退化风险	哈希冲突可能导致性能下降扩容/再哈希开销大	高退化风险有序数据插入→链表O(n)	低风险自平衡结构	极低风险严格自平衡结构
树高控制	无树结构概念	无自动控制高度可能为 n	优秀控制 m阶树高度约log_m n	最佳控制更矮的树，更大扇出
平衡维护	无平衡概念需处理冲突(链地址/开放寻址)	普通BST无平衡平衡变种(AVL/红黑)需旋转，平衡维护成本高	自动平衡分裂/合并操作	自动平衡分裂策略更优
查询效率	等值查询O(1) 范围查询O(n)	O(log n)平均 O(n)最坏(退化)	O(log_m n)	O(log_m n) 实际更快(更矮)
插入/删除	O(1)平均 O(n)最坏(扩容/冲突)	O(log n)平均 O(n)最坏	O(log_m n)	O(log_m n) 更稳定的性能
空间效率	有负载因子空间浪费	每个节点两个指针结构简单	节点存储数据空间利用率约50-100%	更高空间利用率内部节点仅存键，数据全在叶节点
磁盘I/O优化	不适合磁盘存储局部性差	不适合磁盘存储随机访问多	适合磁盘存储节点大小=磁盘页	最适合磁盘存储顺序访问特性，I/O最少
典型应用场景	缓存、字典、集合 ++等值查询++频繁	内存++中小数据集++ 简单排序需求	文件系统、数据库索引 (非关系型)	关系数据库索引大数据范围查询
数据存储位置	键值对分布存储	每个节点存键和数据	每个节点都可能存数据	仅叶节点存数据内部节点只存键
顺序遍历	需要额外排序效率O(n log n)	中序遍历O(n)	需要复杂遍历跨多层级	高效顺序遍历叶节点链表O(n)

2. MySQL中的页

2.1 页的大小、以及为何是这么大

1. 什么是内存页？

内存页 （Page）是操作系统分配内存的最小单位 ，通常大小为 4KB。它是虚拟内存和物理内存之间映射的基本单位。

一条完整的数据不会卡在两个相邻内存页之间，它只能完全存在于其中一页。

2. 什么是MySQL中的页？

MySQL中的页 是InnoDB(.ibd文件) 中管理数据的最小单元 。它的大小通常是 16KB，由4个地址连续的内存页组成。

可以通过系统变量 innodb_page_size 查看页的大小，语法：

show variables like 'innodb_page_size'；

16384个字节，也就是16KB。

3. 为什么要使用连续的4个内存页呢？

（该问题与为什么使用B+树作为索引无关）之所以这样做，是因为在使用数据的过程中会存在局部性原理。局部性通常有两种形式：

时间局部性（TemporalLocality）：如果⼀个信息项正在被访问，那么在近期它很可能还会被再次访问。

空间局部性（SpatialLocality）：将来要用到的信息大概率与正在使用的信息在空间地址上是临近的。

例如上一次查找了select * from student where id > 0 and id <= 20，下一次可能就要查找select * from student where id > 20 and id <= 40，而可能刚好前20条数据保存在1号内存页，后20条数据保存在3号内存页。

空间局部性是 MySQL 采用连续 4 个内存页作为 InnoDB 页的主要原因，因为它可以减少磁盘 I/O 次数，提高数据访问效率。

磁盘IO的成本主要在于寻道时间 （移动磁头到正确位置）和旋转延迟 （等待正确扇区转到磁头下），而不是数据传输时间。++读取4KB++ 和 ++读取连续的16KB++的实际时间相差不大，因为主要时间花在寻道和旋转上，而不是数据传输上。

2.2 页在B+树中的结构

MySQL中的页分为索引页 和数据页。索引页对应B+树中的内部节点（非叶子节点），数据页对应B+树中的叶子节点。
索引页与数据页是一样的大小，都是16KB。

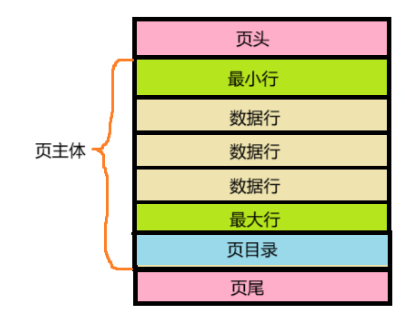
a.页头、页尾、数据行

无论是索引页还是数据页都会包含页头和页尾。

页头与页尾之间是页主体（行记录区域），以"数据行"为单位，用来存储页的主体信息。

页头占38个字节，页尾占8个字节，不同类型的数据行大小不一样。

一个数据库页由多个内存页组成，总共16KB：

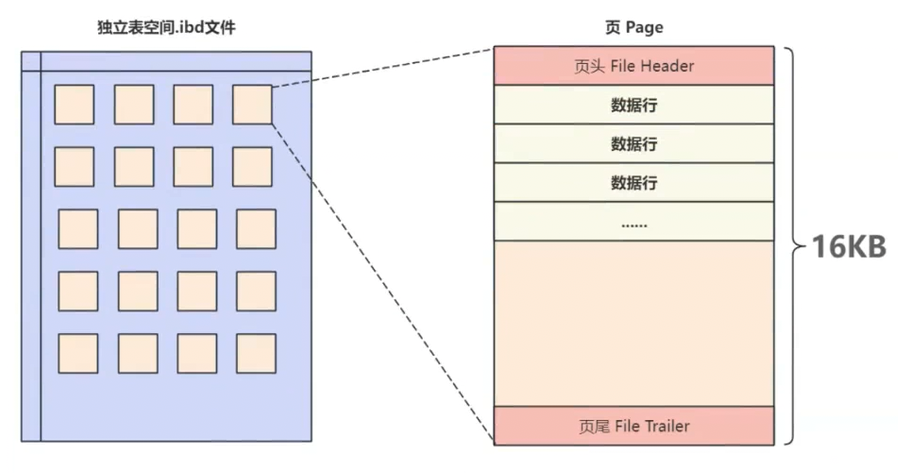
⻚⽂件头和⻚⽂件尾中包含的信息，如下图所示：

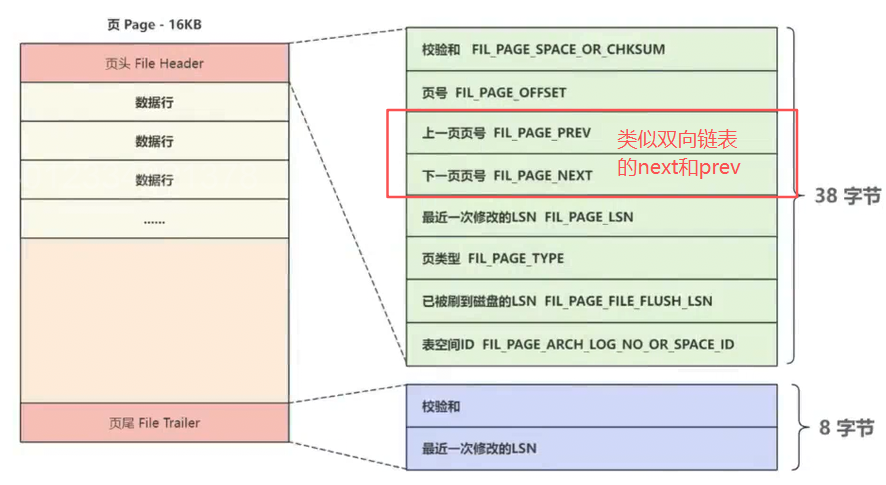
注意：**无论是索引页还是数据页，它们的页头与页尾都如上图所示。 因为在MySQL InnoDB的B+树实现** 中，不只是叶子节点间有双向链表结构，就连同层的内部节点（非叶子节点）也存在双向链表结构。

b.页主体

页主体部分是保存真实数据的主要区域。

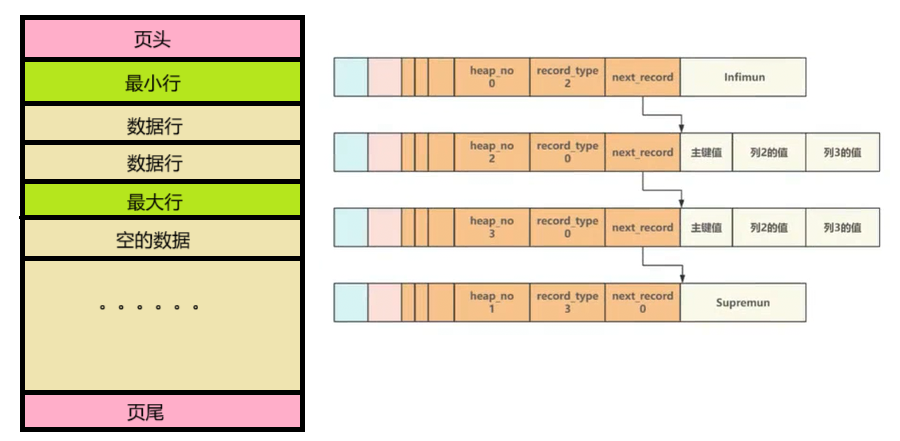
当一个新页被创建时，都会自动初始化两个数据行：页内最小行 （Infimun）和页内最大行（Supremun）。

最小行和最大行并不存储任何真实信息，而是做为数据行链表的头和尾 ，上一数据行的 next_record 指针指向下一数据行，将页内所有数据⾏组成了⼀个单向链表。

初始化时，最小行与最大行是紧挨着的，此时最小行的 next_record 指针指向最大行。

插入数据后，最小行与最大行断开，新数据被插入在最大行的上面。最小行的 next_record 指针指向第一个被插入的数据，由最新插入的数据行的 next_record 指针指向最大行。

随着插入的数据越来越多，最大行离最小行越来越远。最小行的位置永远保持不变；最大行离页尾越来越近，最多可以与页目录行紧挨着。

如下图所示：

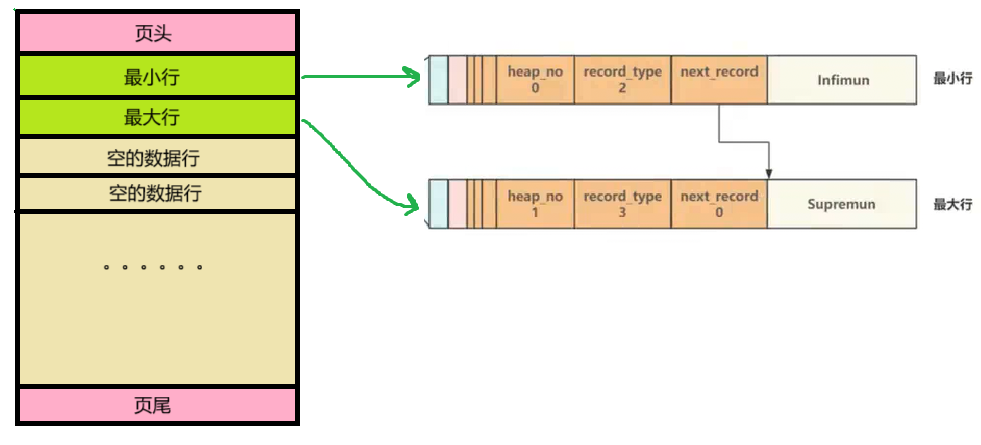
【主键值就是之前我们说的用于排序的键值key】

c.页目录

当按索引查找页内的某条数据时，最直接简单的方法就是从头行 infimun 开始，沿着链表顺序逐个比对，但⼀个⻚有16KB，通常会存在上百行数据，如果每次都要遍历数百⾏，无法满足高效查询。为了提⾼查询效率，InnoDB采⽤页目录来解决页内查询效率的问题。

页目录（Page Directory） 是InnoDB页内部的一个索引结构 ，位于页的末尾 (紧挨在页尾的上方) ，用于快速定位页内的记录。

页目录是由槽构成的 。

对数据行进行分组，约定每4~8个数据行合成一组，⼀旦分组中的数据行超过分组的上限8个时，就会分裂成两个组（有可能是4+4、5+3、6+2）。

一个槽只对应一个组。

一个槽只有2字节 ，它记录了数据行的页内偏移量 ，也就是组的地址 。而组的地址是用组内最后一个数据行的地址来表示。

页头会记录页目录在页中的地址 和页目录中的槽总数。

插入数据时页目录的变化：

页目录的大小是动态变化的，它的大小 = 槽数量 X 2字节。典型情况下 (200-300 条记录)，页目录占用约 20-70 字节，占整个 16KB 页的0.12%-0.43%。

页在初始化时，会在页目录行中自动创建2个槽。序号为0的槽指向最小行，序号为1的槽指向最大行。

随着插入的数据，组数和槽数会越来越多，而最大行永远位于序号最大的组（该组的行数 <= 8） ；但是序号为0的槽永远且唯一指向最小行（该组的行数永远为1）。

例图：【这里为了方便，左边的图把最小行与最大行放一起了，实际上是相隔的】

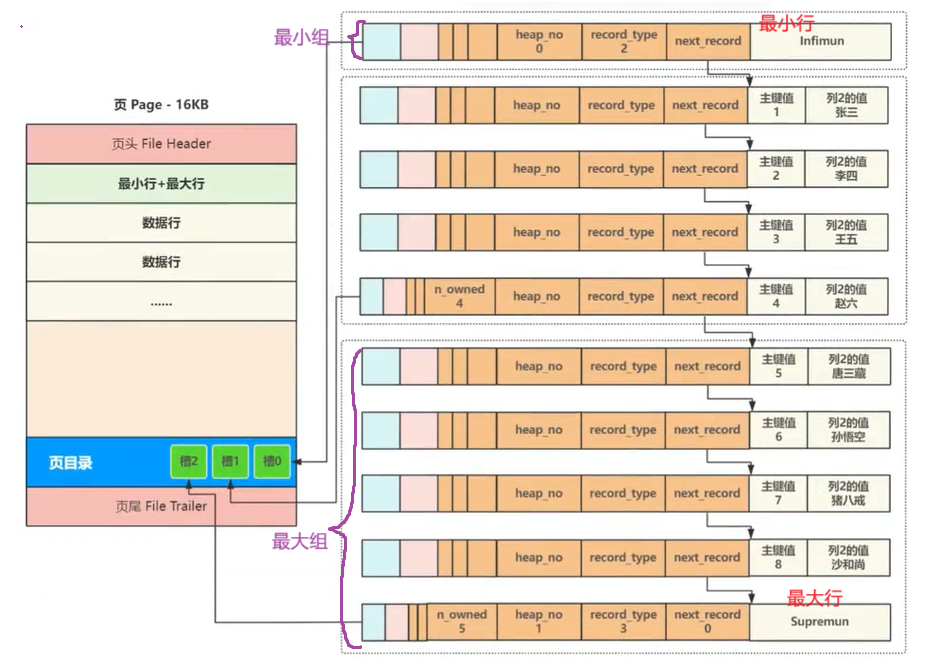
页目录的二分查找找到页内数据行：

步骤 1：确定槽的二分边界

初始化左边界left=0 （第一个槽，对应最小组）、右边界right=槽总数-1 。例：槽总数 = 5 → right=4。

步骤 2：取中间槽，定位组的最大记录

计算中间槽索引：mid = (left + right) / 2。

通过中间槽记录的偏移量，定位到该组的****最后一条记录 并读取该记录的键值（槽本身不存键，需通过行的页内偏移量找到记录后提取）。

步骤 3：比较目标键与组最大键，缩小范围

若目标键 < 组最大键 ：说明目标在left~mid的槽范围内 → 调整right=mid。

若目标键 > 组最大键 ：说明目标在mid+1~right的槽范围内 → 调整left=mid+1。

若目标键 = 组最大键：直接定位到该记录，结束查找。

步骤 4：重复步骤 2-3，直到left >=right

此时left对应的槽，就是目标记录所在的组。

步骤 5：组内反向遍历，找到目标记录

通过left槽的偏移量，定位到该组的最后一条记录，然后向上（反向）遍历组内记录（最多 8 条），找到目标键对应的记录。如果找不到说明不存在目标键的记录。

数据行之间是单链表，在++逻辑层面上无法反向遍历++。不过我们可以在物理层面上反向遍历：

页是由一个个存储单元构成的，存储单元可以物理寻址，只需要通过槽找到组内最大键值的地址 ，然后通过**每次减去当前数据行的大小（数据行中会有专门字段记录行的大小）**就可以找到上一条记录。

问：为什么槽指向的是组内最后一个数据，而不是指向组内第一个数据？

假设：槽指向组内第一条记录

情况 1：目标键存在，且目标键位于最小行的下一行 。从槽 0 对应的组（最小行）向后遍历，只需 1 次比较就能找到，效率和现实场景一致。
情况 2：目标键不存在，且目标键大于最大组的最大键 。因为槽此时指向++组的最小键++ ，需要遍历整个组（最多 8 条记录），直到确认组内所有键都小于目标键，才能判定 "不存在"------ 最多要比较 8 次。

现实：槽指向组内最后一条记录

情况 1：目标键存在，且目标键位于最小行的下一行 。从槽 0 对应的组最后一条记录反向遍历，同样只需 1 次比较就能找到，效率不变。
情况 2：目标键不存在，且目标键大于最大组的最大键 。槽直接关联组的最大键，只需将目标键与 "最大组的最大键" 比较 1 次：若目标键更大，直接判定 "不存在"------ 无需遍历组内记录，效率大幅提升。

槽指向组内最后一条记录，既不影响 "目标键是页内最小键时" 的查找效率，又能把 "目标键是页内最大键时" 的比较次数从最多 8 次压缩到 1 次，同时还契合二分查找的区间判断逻辑，是更高效的设计。

#2# 总结页结构的异同

1. MySQL中索引页和数据页的相同之处：

两者都是16KB大小。

两者都含有页头、页主体 和页尾。且在MySQL中，两者都具有双向链表结构，它们的页头都含有字段：上一页页号、下一页页号。

两者的页主体内部都含有：最小行 、最大行 、页目录 和普通数据行。

两者的普通数据行内部都含有存储键值的字段。

2. MySQL中索引页和数据页的不同之处：

数据行内部存储的键值：

在索引页中作为路由键，用于给子节点划分区间。

在数据页中作为数据键，存储的是真实的数据。

数据行中，"键值"字段后面的字段 ：

在索引页中：路由键 + 子节点指针。

子节点指针指向的是由路由键划分的右区间子节点。

最左区间指针 存放在++最小行的下一行++，该数据行是不存在"键值"字段的。

第一个路由键 存储在++最小行的下面第2个数据行++。

在数据页中：数据键 + 与真实表相关的字段

使用的索引是++聚簇索引++ ：数据键（主键） + 真实表所有字段（无额外指针，本身就是真实表行）

使用的索引是++非聚簇索引++ ：数据键（索引键） + 真实表的行指针（主键值）（通过指针进行回表查询找到真实数据）

本期分享完毕，感谢大家的支持Thanks♪(･ω･)ﾉ