代码随想录 300.最长递增子序列

风筝在晴天搁浅2025-12-06 11:31

思路：根据题意得，子序列是由数组派生而来的序列，删除（或不删除）数组中的元素不改变其余元素的顺序。

动规五部曲：

1.dp[i]的定义：dp[i]表示i之前包括i的以nums[i]结尾的最长递增子序列的长度。

2.确定递推公式（状态转移方程）：

（1）位置i的最长递增子序列等于j从0到i - 1各个位置的最长递增子序列 + 1的最大值。

（2）所以：if(nums[i] > nums[j]) dp[i] = max(dp[i],dp[j] + 1)。（这里不是将dp[i]与dp[j] + 1比较，而是选取dp[j] + 1的最大值）。

3.dp[i]的初始化：每一个i，对应的dp[i]（即最长递增子序列）起始大小至少都是1。

4.确定遍历顺序：

（1）dp[i]是由0到i - 1各个位置的最长递增子序列推导而来，因此遍历i一定是从前向后遍历。

（2）j就是遍历0到i - 1，因此从前到后或从后到前的遍历顺序都无所谓，只要把0到i - 1的元素都遍历到就行。默认习惯为从前到后遍历。

遍历i的循环在外层，遍历j的循环在内层，代码如下所示：

cpp 复制代码

for (int i = 1; i < nums.size(); i++) {
    for (int j = 0; j < i; j++) {
        if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
    }
    if (dp[i] > result) result = dp[i]; // 取长的子序列
}

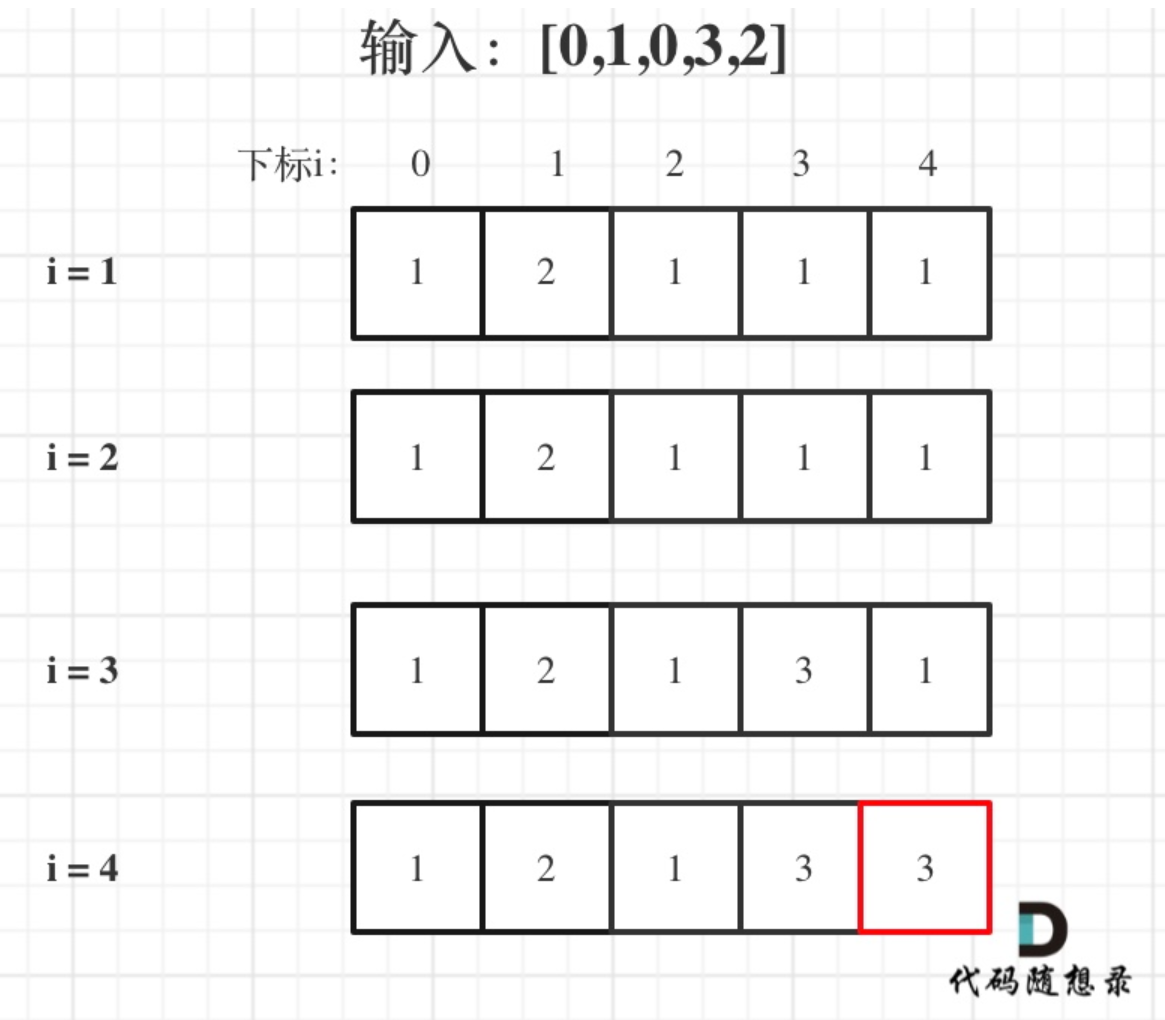
5.举例推导dp数组：输入：[0,1,0,3,2],dp数组的变化如下所示。

附代码：

java 复制代码

class Solution {
    public int lengthOfLIS(int[] nums) {
        if(nums.length <= 1){
            return nums.length;
        }
        int res = 1;
        int[] dp = new int[nums.length];
        for(int i = 0;i < nums.length;i++){
            dp[i] = 1;
        }
        for(int i = 1;i < nums.length;i++){
            for(int j = 0;j < i;j++){
                if(nums[i] > nums[j]){
                    dp[i] = Math.max(dp[i],dp[j] + 1);
                }
            }
            res = Math.max(res,dp[i]);
        }
        return res;
    }
}