C++：queue、priority_queue的使用和模拟实现

1 queue的介绍和使用

1.1 queue的介绍

队列是一种容器适配器 ，专门用于在**FIFO上下文(先进先出)**中操作，其中从容器一端插入元素，另一端提取元素。

队列作为容器适配器实现，容器适配器即将特定容器类封装作为其底层容器类，queue提供一组特定的成员函数来访问其元素。元素从队尾入队列，从队头出队列。

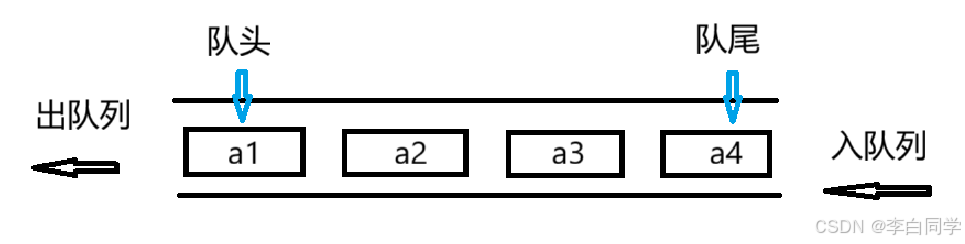
2.2 queue的使用

|----------|----------------------------|
| 函数声明 | 接口说明 |
| queue() | 构造空的队列 |
| empty() | 检测队列是否为空，是返回true，否则返回false |
| size() | 返回队列中有效元素的个数 |
| front() | 返回队头元素的引用 |
| back() | 返回队尾元素的引用 |
| push() | 在队尾将元素val入队列 |
| pop() | 将队头元素出队列 |

题目：

225. 用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。
int pop() 移除并返回栈顶元素。
int top() 返回栈顶元素。
boolean empty() 如果栈是空的，返回 true ；否则，返回 false 。

注意：

你只能使用队列的标准操作 ------ 也就是 push to back、peek/pop from front、size 和 is empty 这些操作。
你所使用的语言也许不支持队列。你可以使用 list （列表）或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。

示例：

复制代码

输入：
["MyStack", "push", "push", "top", "pop", "empty"]
[[], [1], [2], [], [], []]
输出：
[null, null, null, 2, 2, false]

解释：
MyStack myStack = new MyStack();
myStack.push(1);
myStack.push(2);
myStack.top(); // 返回 2
myStack.pop(); // 返回 2
myStack.empty(); // 返回 False

提示：

1 <= x <= 9
最多调用100 次 push、pop、top 和 empty
每次调用 pop 和 top 都保证栈不为空

**进阶：**你能否仅用一个队列来实现栈。

解答：

cpp 复制代码

class MyStack {
public:
    MyStack() {
        
    }
    
    void push(int x) {
        _q2.push(x);
        while(!_q1.empty())
        {
            _q2.push(_q1.front());
            _q1.pop();
        }
        swap(_q1, _q2);
    }
    
    int pop() {
        int top = _q1.front();
        _q1.pop();
        return top;
    }
    
    int top() {
        int top = _q1.front();
        return top;
    }
    
    bool empty() {
        return _q1.empty() && _q2.empty();
    }
private:
    queue<int> _q1;
    queue<int> _q2;
};

/**
 * Your MyStack object will be instantiated and called as such:
 * MyStack* obj = new MyStack();
 * obj->push(x);
 * int param_2 = obj->pop();
 * int param_3 = obj->top();
 * bool param_4 = obj->empty();
 */

2.3 queue的模拟实现

cpp 复制代码

#pragma once
#include <vector>
#include <list>
#include <deque>

namespace room
{
	// 传模板参数可以这样给 - 这里只能用 list 适配；因为 vector 没有提供 pop_front()
	// queue<int, list<int>>
	// 给一个容器模板 Container，这样就不会写死
	// Container = list<int> 默认容器是 list
	//template<class T, class Container = list<T>>
	template<class T, class Container = deque<T>>	// deque 头尾插入删除效率很高
	class queue
	{
	public:
		void push(const T& x)
		{
			_con.push_back(x);
		}

		void pop()
		{
			//_con.erase(_con.begin());	// 这样的话就能支持 vector，但是效率太低了
			_con.pop_front();
		}

		const T& front()
		{
			return _con.front();
		}

		const T& back()
		{
			return _con.back();
		}

		size_t size() const
		{
			return _con.size();
		}

		bool empty()
		{
			return _con.empty();
		}

	private:
		Container _con;	// 想要数组栈就传 vector<int>；想要链式栈就传 list<int>
	};
};

2 priority_queue的介绍和使用

2.1 priority_queue的介绍

priority_queue - C++ Reference

优先队列是一种容器适配器 ，根据严格的弱排序标准，它的第一个元素总是它所包含的元素中最大的。此上下文类似于堆，在堆中可以随时插入元素，并且只能检索最大堆元素(优先队列中位于顶部的元素)。

优先队列被实现为容器适配器，容器适配器即将特定容器类封装作为其底层容器类，queue提供一组特定的成员函数来访问其元素。元素从特定容器的"尾部"弹出，其称为优先队列的顶部。

2.2 priority_queue的使用

优先级队列默认使用vector作为其底层存储数据的容器，在vector上又使用了堆算法将vector中元素构造成堆的结构，因此priority_queue就是堆 ，所有需要用到堆的位置，都可以考虑使用priority_queue。注意：默认情况下priority_queue是大堆。

|----------------------------------------------|-------------------------------|
| 函数声明 | 接口说明 |
| priority_queue()/priority_queue(first, last) | 构造一个空的优先级队列 |
| empty( ) | 检测优先级队列是否为空，是返回true，否则返回false |
| top( ) | 返回优先级队列中最大(最小元素)，即堆顶元素 |
| push(x) | 在优先级队列中插入元素x |
| pop() | 删除优先级队列中最大(最小)元素，即堆顶元素 |

用法：

1.默认是大堆

cpp 复制代码

#include <vector>
#include <queue>
#include <functional>

void TestPriorityQueue()
{
    // 默认情况下，创建的是大堆，其底层按照小于号比较
    vector<int> v{3,2,7,6,0,4,1,9,8,5};
    priority_queue<int> q1;
    for (auto& e : v)
    q1.push(e);
    cout << q1.top() << endl;
    // 如果要创建小堆，将第三个模板参数换成greater比较方式
    priority_queue<int, vector<int>, greater<int>> q2(v.begin(), v.end());
    cout << q2.top() << endl;
}

int main()
{
    TestPriorityQueue();

    return 0; 
}

结果：

2.priority_queue中放自定义类型的数据，用户需要在自定义类型中提供> 或者< 的重载。

cpp 复制代码

class Date
{
	friend ostream& operator<<(ostream& _cout, const Date& d);
public:
	Date(int year = 2025, int month = 8, int day = 26)
		: _year(year)
		, _month(month)
		, _day(day)
	{}

	bool operator<(const Date& d) const
	{
		return (_year < d._year) ||
			(_year == d._year && _month < d._month) ||
			(_year == d._year && _month == d._month && _day < d._day);
	}

	bool operator>(const Date& d) const
	{
		return (_year > d._year) ||
			(_year == d._year && _month > d._month) ||
			(_year == d._year && _month == d._month && _day > d._day);
	}

private:
	int _year;
	int _month;
	int _day;
};

ostream& operator<<(ostream& _cout, const Date& d)
{
	_cout << d._year << "-" << d._month << "-" << d._day;
	return _cout;
}

struct LessPDate
{
	bool operator()(Date* p1, Date* p2)
	{
		return *p1 < *p2;
	}
};

int main()
{
	//priority_queue<Date> q1;
	room::priority_queue<Date, vector<Date>, greater<Date>> q1;
	q1.push(Date(2025, 10, 29));
	q1.push(Date(2025, 10, 28));
	q1.push(Date(2025, 10, 30));
	while (!q1.empty())
	{
		std::cout << " " << q1.top();
		q1.pop();
	}
	std::cout << std::endl;

	// 这样写就会有问题
	//priority_queue<Date*> q2;
	room::priority_queue<Date*, vector<Date*>, LessPDate> q2;	// 这样就是好
	q2.push(new Date(2025, 10, 29));
	q2.push(new Date(2025, 10, 28));
	q2.push(new Date(2025, 10, 30));
	while (!q2.empty())
	{
		std::cout << " " << *q2.top();
		q2.pop();
	}
	std::cout << std::endl;

	return 0;
}

结果：

3.题目

215. 数组中的第K个最大元素

给定整数数组 nums 和整数 k，请返回数组中第 k 个最大的元素。

请注意，你需要找的是数组排序后的第 k 个最大的元素，而不是第 k 个不同的元素。

你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1:

复制代码

输入: [3,2,1,5,6,4], k = 2
输出: 5

示例 2:

复制代码

输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4

提示：

1 <= k <= nums.length <= 105
-104 <= nums[i] <= 104

解答：

cpp 复制代码

class Solution {
    int quickSort(vector<int>& nums, int k)
    {
        // 随机选择基准数
        int key = nums[rand() % nums.size()];
        // 将大于、小于、等于 key 的元素划分至 big, small, equal
        vector<int> big, equal, small;
        for(int num : nums)
        {
            if(num > key)
                big.push_back(num);
            else if(num < key)
                small.push_back(num);
            else
                equal.push_back(num);
        }

        // 将 k 大的元素在 big 中，递归划分
        if(k <= big.size())
            return quickSort(big, k);
        // 将 k 大的元素在 small 中，递归划分
        if(nums.size() - small.size() < k)
            return quickSort(small, k - nums.size() + small.size());
        // 第 k 大的元素在 equal 中，直接返回 key
        return key;
    }
public:
    int findKthLargest(vector<int>& nums, int k) {
        return quickSort(nums, k);
    }
};

2.3 priority_queue的模拟实现

priority_queue的底层结构就是堆，因此此处只需对进行通用的封装即可。

cpp 复制代码

#pragma once
#include <vector>

namespace room
{
	// 没有仿函数
	//template<class T, class Container = vector<T>>
	//class priority_queue
	//{
	//public:
	//	void adjust_up(size_t child)
	//	{
	//		size_t parent = (child - 1) / 2;
	//		while (child > 0)
	//		{
	//			if (_con[child] > _con[parent])
	//			{
	//				swap(_con[child], _con[parent]);
	//				child = parent;
	//				parent = (child - 1) / 2;
	//			}
	//			else
	//			{
	//				break;
	//			}
	//		}
	//	}

	//	void adjust_down(size_t parent)
	//	{
	//		size_t child = parent * 2 + 1;	// 假设左孩子大
	//		while (child < _con.size())
	//		{
	//			if (child + 1 < _con.size() && _con[child + 1] > _con[child])
	//			{
	//				++child;
	//			}

	//			if (_con[child] > _con[parent])
	//			{
	//				swap(_con[child], _con[parent]);
	//				parent = child;
	//				child = parent * 2 + 1;
	//			}
	//			else
	//			{
	//				break;
	//			}
	//		}
	//	}

	//	void push(const T& x)
	//	{
	//		_con.push_back(x);
	//		adjust_up(_con.size() - 1);
	//	}

	//	void pop()
	//	{
	//		swap(_con[0], _con[_con.size() - 1]);
	//		_con.pop_back();
	//		adjust_down(0);
	//	}

	//	const T& top()
	//	{
	//		return _con[0];
	//	}

	//	size_t size()
	//	{
	//		return _con.size();
	//	}

	//	bool empty()
	//	{
	//		return _con.empty();
	//	}

	//private:
	//	Container _con;
	//};

	// 仿函数/函数对象
	// 实质：重载 operator()
	template<class T>
	class Less
	{
	public:
		bool operator()(const T& x, const T& y)
		{
			return x < y;
		}
	};

	template<class T>
	class Greater
	{
	public:
		bool operator()(const T& x, const T& y)
		{
			return x > y;
		}
	};

	// 默认是大堆
	template<class T, class Container = vector<T>, class Compare = Less<T>>
	class priority_queue
	{
	public:
		void adjust_up(size_t child)
		{
			Compare com;
			size_t parent = (child - 1) / 2;
			while (child > 0)
			{
				//if (_con[parent] < _con[child])
				if(com(_con[parent], _con[child]))
				{
					swap(_con[parent], _con[child]);
					child = parent;
					parent = (child - 1) / 2;
				}
				else
				{
					break;
				}
			}
		}

		void adjust_down(size_t parent)
		{
			Compare com;
			size_t child = parent * 2 + 1;
			while (child < _con.size())
			{
				//if (child + 1 < _con.size() && _con[child] < _con[child + 1])
				if(child + 1 < _con.size() && com(_con[child], _con[child + 1]))
				{
					++child;
				}

				//if(_con[parent] < _con[child])
				if (com(_con[parent], _con[child]))
				{
					swap(_con[parent], _con[child]);
					parent = child;
					child = parent * 2 + 1;
				}
				else
				{
					break;
				}
			}
		}

		void push(const T& x)
		{
			_con.push_back(x);
			adjust_up(_con.size() - 1);
		}

		void pop()
		{
			swap(_con[0], _con[_con.size() - 1]);
			_con.pop_back();
			adjust_down(0);
		}
		const T& top()
		{
			return _con[0];
		}

		size_t size()
		{
			return _con.size();
		}

		bool empty()
		{
			return _con.empty();
		}

	private:
		Container _con;
	};
};