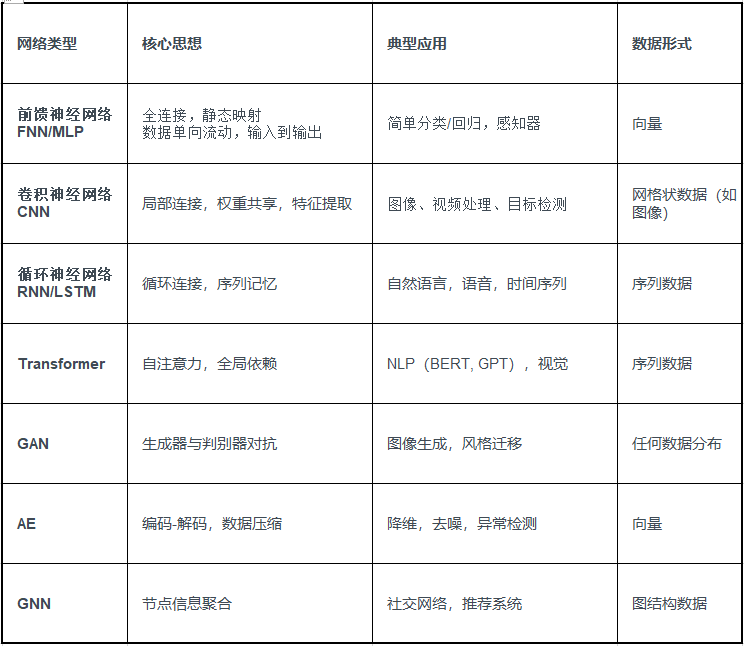
一、常见神经网络算法
二、前馈神经网络
1、结构
1)输入层 (Input Layer):接收外部输入信号。
2)隐藏层 (Hidden Layer):对输入信号进行处理和特征提取,可以有多个隐藏层。
3)输出层(Output Layer):产生最终的输出结果。
2、工作原理
如下四层网络:
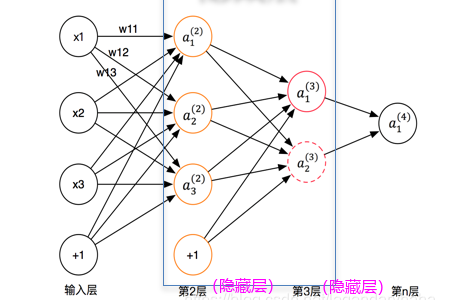
1) 前向传播 :
输入数据首先进入输入层,然后通过权重和偏置传递到隐藏层,隐藏层中的节点对输入进行加权求和,并通过激活函数进行非线性转换,最后输出层接收到经过隐藏层处理的信号,并产生最终的输出。
2)激活函数 :
激活函数用于在网络中引入非线性,将输入数据映射到一个特定的范围。常见的激活函数包括Sigmoid、Tanh、ReLU等。
激活函数特点:
***logsig:数值范围是0~1,多次经过变换可能会导致数据的相对比例关系发生改变,因为函数的非线性特性会使不同输入值之间的差异在映射后产生不同的变化。
***tansig:数值范围是-1~1,数据在经历了多重的Sigmoid变换后仍维持原先的比例关系。
3)权重和偏置:权重是连接输入层和隐藏层、隐藏层和输出层的连接强度,偏置是加在输入上的一个常数,用于调整激活函数的输出。
3、训练过程
1)损失函数 :定义一个损失函数来衡量模型预测值与实际值之间的差异,常见的损失函数包括均方误差(MSE)、交叉熵损失等。
2)反向传播 :虽然称为反向传播,但在前馈神经网络中,它实际上是在训练过程中使用的,用于计算损失函数关于权重的梯度。
3)优化算法:通过最小化损失函数来更新网络权重,常见的优化算法包括随机梯度下降(SGD)或其变体Adam、RMSProp等
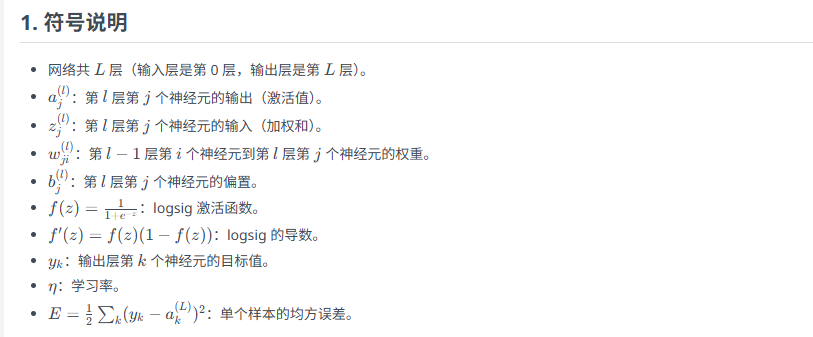
公式总结
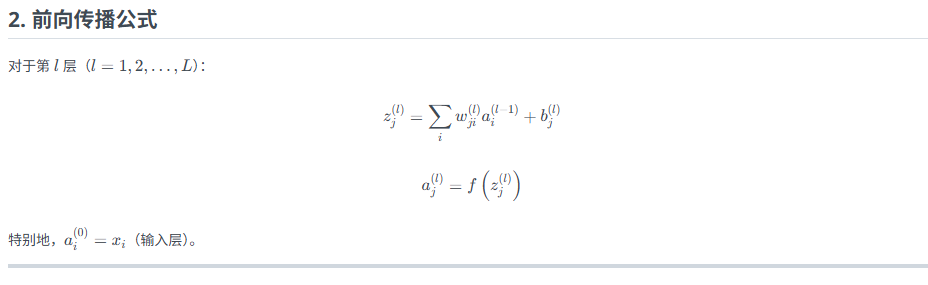

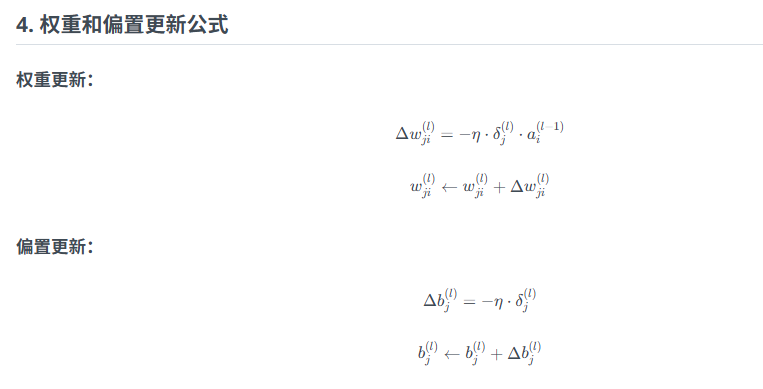
4、注意
4.1 特点
前馈神经网络初始权重是随机的,后续权重更新是在前一个样本更新后的权重基础上,
即每个样本更新一次权重。
迭代次数=训练轮数*样本数量
1.反向传播顺序:从输出层开始,逐层向后计算δ,再用前向传播时保存的 a (l)和旧权重 计算梯度。
2.在线学习(随机梯度下降):每个样本更新一次权重。
批量学习:所有样本前向传播后,累加每个样本的 Δw 和 Δb然后求平均(或总和)再更新。
3.logsig 特性:导数可用激活值直接计算,无需重新计算 z
4.2 优化
如果想要更精确的收敛,可以:
1降低学习率
2 增加迭代轮数
3*使用批量梯度下降(多个样本的总误差一起求平均再更新)
4.3 隐藏层数怎么选:
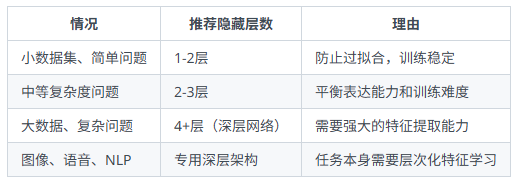
层数过多的问题:
1*梯度消失/爆炸问题
梯度我理解为权重变换量
2*过拟合风险
过拟合,即训练误差小,测试误差大
3*训练难度和计算成本
层数越多,参数越多
4*单层隐藏层已经可以拟合任何连续函数。