【人工智能】【深度学习】 ⑦ 从零开始AI学习路径：从Python到大模型的实战指南

📖目录

前言
[1. 为什么你需要系统学习？（不是随便找个教程就能学会的）](#1. 为什么你需要系统学习？（不是随便找个教程就能学会的）)
[2. 学习路径总览（一张图看懂全流程）](#2. 学习路径总览（一张图看懂全流程）)
[3. 第一阶段：Python基础（1-2个月）](#3. 第一阶段：Python基础（1-2个月）)
- [3.1 Python核心基础](#3.1 Python核心基础)
- [3.2 为什么学Python？（不是因为"简单"，而是因为"生态"）](#3.2 为什么学Python？（不是因为“简单”，而是因为“生态”）)
[4. 第二阶段：数学基础（2-3个月） - 为什么数学是AI的"地基"？](#4. 第二阶段：数学基础（2-3个月） - 为什么数学是AI的“地基”？)
- [4.1 微积分：变化的艺术（速度、加速度、最优点）](#4.1 微积分：变化的艺术（速度、加速度、最优点）)
- - [4.1.1 导数：变化率（速度计）](#4.1.1 导数：变化率（速度计）)
  - [4.1.2 积分：累积效应（里程表）](#4.1.2 积分：累积效应（里程表）)
  - [4.1.3 极限：无限逼近（无限接近但不接触）](#4.1.3 极限：无限逼近（无限接近但不接触）)
- [4.2 概率论：不确定性的数学（猜拳、抽奖、天气预报）](#4.2 概率论：不确定性的数学（猜拳、抽奖、天气预报）)
- - [4.2.1 概率分布：可能性的分布（彩票中奖率）](#4.2.1 概率分布：可能性的分布（彩票中奖率）)
  - [4.2.2 贝叶斯定理：更新信念（根据新信息调整判断）](#4.2.2 贝叶斯定理：更新信念（根据新信息调整判断）)
  - [4.2.3 期望与方差：平均与波动（投资回报率 vs 风险）](#4.2.3 期望与方差：平均与波动（投资回报率 vs 风险）)
- [4.3 线性代数：矩阵的世界（网格地图 + 数据表格）](#4.3 线性代数：矩阵的世界（网格地图 + 数据表格）)
- - [4.3.1 矩阵乘法：多步骤运算（快递配送路径）](#4.3.1 矩阵乘法：多步骤运算（快递配送路径）)
  - [4.3.2 矩阵分解：拆解复杂关系（快递分拣）](#4.3.2 矩阵分解：拆解复杂关系（快递分拣）)
[5. 第三阶段：机器学习（3-4个月）](#5. 第三阶段：机器学习（3-4个月）)
- [5.1 机器学习核心概念](#5.1 机器学习核心概念)
- [5.2 机器学习实战：房价预测](#5.2 机器学习实战：房价预测)
[6. 第四阶段：深度学习（3-4个月）](#6. 第四阶段：深度学习（3-4个月）)
- [6.1 深度学习核心概念](#6.1 深度学习核心概念)
- [6.2 深度学习实战：MNIST手写数字识别](#6.2 深度学习实战：MNIST手写数字识别)
[7. 第五阶段：大模型（3-4个月）](#7. 第五阶段：大模型（3-4个月）)
- [7.1 大模型核心概念](#7.1 大模型核心概念)
- [7.2 大模型实战：用Hugging Face实现文本生成](#7.2 大模型实战：用Hugging Face实现文本生成)
[8. 经典书目推荐（真正有用的）](#8. 经典书目推荐（真正有用的）)
[9. 附录：数学公式与代码对照表](#9. 附录：数学公式与代码对照表)
[10. 总结：AI学习不是"学技术"，而是"学思维"](#10. 总结：AI学习不是“学技术”，而是“学思维”)
[11. 附：系列博文链接](#11. 附：系列博文链接)

前言

【写在前面】

作为一个在AI领域摸爬滚打十年的老码农，我见过太多人想学AI却无从下手。不是因为技术太难，而是因为没有一条清晰、可执行的学习路径。

本文不是"速成指南"，而是真正从零开始的系统学习路线 ，包含每个阶段的核心内容、学习资源、避坑建议和实战代码。

为什么这篇文章值得你认真读？因为我亲自走过这条路，也帮过身边的数位朋友规划学习路径。下面，让我们一起踏上这段旅程。

1. 为什么你需要系统学习？（不是随便找个教程就能学会的）

很多人以为AI就是"调用API"、"写几个神经网络"，但事实是：

90%的AI项目失败，是因为基础不牢（数据、特征、模型选择）
AI不是魔法，是工程（需要扎实的数学+编程+业务理解）
没有系统路径，你会在"学Python"和"学Transformer"之间反复横跳

任正非说 ："不要幻想一步登天，要小步快跑，先在一个点上打穿。 "

------ 这句话同样适用于AI学习。

2. 学习路径总览（一张图看懂全流程）

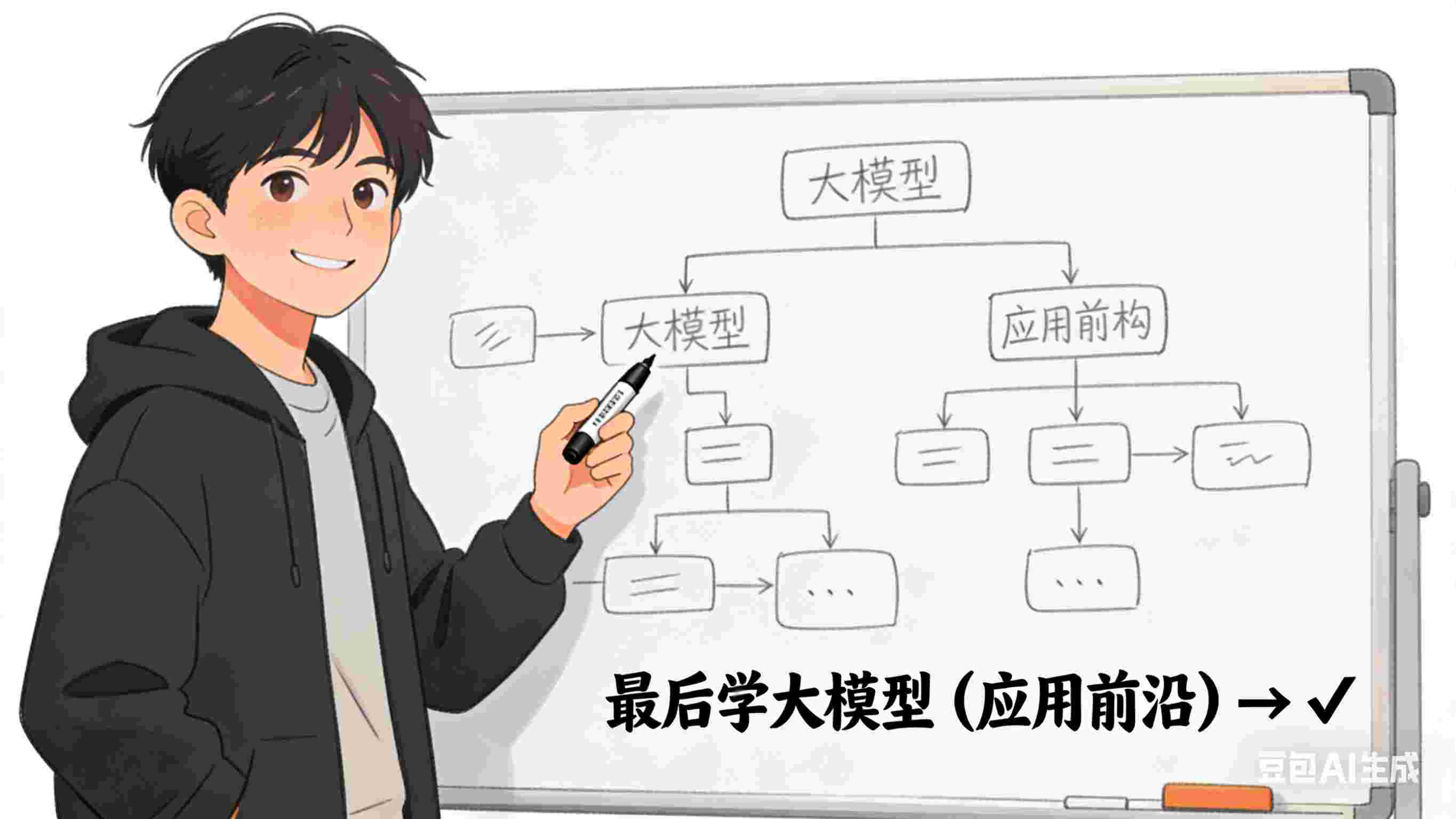
（图1：AI学习路径总览。从基础到大模型，每一步都是下一站的基础）

核心思想 ：

✅ 先打好基础 （数学、编程）→ ✅ 再学机器学习 （理解原理）→ ✅ 再学深度学习 （掌握工具）→ ✅ 最后学大模型（应用前沿）

3. 第一阶段：Python基础（1-2个月）

为什么从Python开始？

因为90%的AI框架（TensorFlow、PyTorch）都用Python，而且Python语法简单，适合初学者。

3.1 Python核心基础

python 复制代码

# 1. 变量与数据类型（就像超市货架上的商品）
name = "小明"  # 字符串：代表人名
age = 25       # 整数：代表年龄
height = 1.75  # 浮点数：代表身高
is_student = True  # 布尔值：代表是否是学生


# 2. 条件语句（就像过红绿灯）
if age >= 18:
    print("可以开车了！")  # 绿灯：执行
else:
    print("还需要等几年")  # 红灯：不执行


# 3. 循环（就像每天重复做早餐）
for i in range(7):  # 重复7天
    print(f"第{i+1}天，吃鸡蛋饼")

3.2 为什么学Python？（不是因为"简单"，而是因为"生态"）

语言	适用场景	AI生态	学习曲线
Python	数据科学、AI	⭐⭐⭐⭐⭐	简单
Java	企业级应用	⭐⭐	中等
C++	系统级开发	⭐	困难

结论：Python是AI的"通用语言"，就像英语是国际交流的通用语言。

4. 第二阶段：数学基础（2-3个月） - 为什么数学是AI的"地基"？

数学不是障碍，而是桥梁。它帮你把"直觉"转化为"算法"，把"经验"转化为"模型"。

4.1 微积分：变化的艺术（速度、加速度、最优点）

4.1.1 导数：变化率（速度计）

核心公式：

f ′ ( x ) = lim ⁡ h → 0 f ( x + h ) − f ( x ) h f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} f′(x)=h→0limhf(x+h)−f(x)

大白话解释：

想象你在开车，仪表盘上的"速度计"显示的是瞬时速度（导数）。

f ( x ) f(x) f(x)：你当前位置

f ( x + h ) f(x+h) f(x+h)：你向前开了一小段路后的位置

h h h：开的这段路有多短（趋近于0）

实战场景：

优化问题：梯度下降法中，导数告诉我们"该往哪个方向走"才能最快下山。

4.1.2 积分：累积效应（里程表）

核心公式：

∫ a b f ( x ) d x = F ( b ) − F ( a ) \int_a^b f(x) dx = F(b) - F(a) ∫abf(x)dx=F(b)−F(a)

大白话解释：

想象你在高速上匀速行驶，速度 × 时间 = 总路程。

f ( x ) f(x) f(x)：每一刻的速度

∫ a b f ( x ) d x \int_a^b f(x) dx ∫abf(x)dx：从时间a到时间b的总路程

实战场景：

计算损失函数的总面积（如交叉熵损失）
累计概率（如正态分布下的概率区域）

4.1.3 极限：无限逼近（无限接近但不接触）

核心思想：

想象你无限接近一个目标，但永远不能完全到达。比如：

分蛋糕：每次切一半，永远吃不完
无限循环小数：0.999... = 1（数学上成立）

在AI中的作用：

定义导数和积分的基础
理解神经网络训练中的收敛性（模型最终会稳定下来）

4.2 概率论：不确定性的数学（猜拳、抽奖、天气预报）

4.2.1 概率分布：可能性的分布（彩票中奖率）

核心概念：

离散分布：抛硬币（0.5概率正面，0.5反面）
连续分布：人的身高（正态分布）

实战场景：

分类问题：预测"这封邮件是垃圾邮件的概率是80%"
生成模型：GANs、VAEs依赖概率分布生成新数据

4.2.2 贝叶斯定理：更新信念（根据新信息调整判断）

核心公式：

P ( A ∣ B ) = P ( B ∣ A ) ⋅ P ( A ) P ( B ) P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)} P(A∣B)=P(B)P(B∣A)⋅P(A)

大白话解释：

你朋友说："我看到一个穿红衣服的人。"

P ( A ) P(A) P(A)：女生的概率（先验概率）

P ( B ∣ A ) P(B|A) P(B∣A)：女生穿红衣服的概率

P ( B ) P(B) P(B)：穿红衣服的总概率

P ( A ∣ B ) P(A|B) P(A∣B)：穿红衣服的人是女生的概率（后验概率）

实战场景：

医疗诊断：结合病史和检查结果更新患病概率
推荐系统：根据用户行为更新推荐策略

4.2.3 期望与方差：平均与波动（投资回报率 vs 风险）

核心公式：

期望： E [ X ] = ∑ x i p i \mathbb{E}[X] = \sum x_i p_i E[X]=∑xipi
方差： Var ( X ) = E [ ( X − E [ X ] ) 2 ] \text{Var}(X) = \mathbb{E}[(X - \mathbb{E}[X])^2] Var(X)=E[(X−E[X])2]

大白话解释：

想象你投资两个项目：

项目A：90%概率赚100元，10%概率赚0元 → 期望90元
项目B：50%概率赚200元，50%概率亏100元 → 期望50元

方差告诉你：项目A更"稳"，项目B更"刺激"。

实战场景：

强化学习：平衡探索（高方差）与利用（低方差）
模型评估：衡量预测结果的稳定性

4.3 线性代数：矩阵的世界（网格地图 + 数据表格）

4.3.1 矩阵乘法：多步骤运算（快递配送路径）

核心公式：

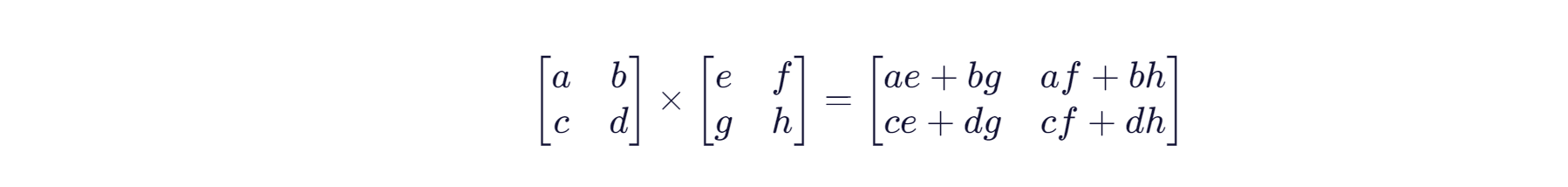
大白话解释：

想象你有两个仓库（A和B），每个仓库卖两种商品（X和Y）：

A仓：X卖1元，Y卖2元
B仓：X卖3元，Y卖4元

两位顾客分别买了：

顾客1：1个X，2个Y
顾客2：2个X，1个Y

矩阵乘法告诉你：顾客1在A仓花11+2 2=5元，在B仓花13+24=11元

实战场景：

神经网络：输入层 × 权重矩阵 = 隐藏层
图像处理：图片（矩阵） × 卷积核（小矩阵） = 特征图

4.3.2 矩阵分解：拆解复杂关系（快递分拣）

核心概念：

SVD分解：把矩阵拆解成"用户-特征-物品"三部分
QR分解：求解线性方程组的稳定方法

大白话解释：

想象你是一个快递分拣员，收到一堆包裹：

有些包裹是"大件"，有些是"易碎品"
SVD分解就像把包裹分类：用户类型 × 包裹特征 × 商家类型

实战场景：

推荐系统：用户-物品矩阵的低秩分解
PCA降维：通过特征分解保留最大方差方向

5. 第三阶段：机器学习（3-4个月）

为什么学机器学习？

因为机器学习是AI的"基础框架"，没有它，深度学习就是空中楼阁。

5.1 机器学习核心概念

概念	大白话解释	代码示例
监督学习	有标签的数据学习（如：已知"猫"和"狗"的图片）	`model.fit(X_train, y_train)`
无监督学习	无标签的数据学习（如：只给图片，不告诉是什么）	`kmeans.fit(X)`
过拟合	模型太"聪明"，记住了训练数据，但不通用	`模型在训练集上99%准确，测试集上50%`

5.2 机器学习实战：房价预测

python 复制代码

# 导入必要的库
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
import matplotlib.pyplot as plt

# 1. 加载数据（假设我们有房价数据）
data = pd.read_csv('housing_data.csv')  # 读取房价数据

# 2. 数据预处理（清理数据，去掉缺失值）
data = data.dropna()

# 3. 特征选择（我们用"面积"预测"房价"）
X = data[['area']]  # 特征：面积
y = data['price']   # 目标：房价

# 4. 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 5. 创建线性回归模型
model = LinearRegression()

# 6. 训练模型
model.fit(X_train, y_train)

# 7. 预测
predictions = model.predict(X_test)

# 8. 评估模型
print(f"模型准确率: {model.score(X_test, y_test):.2f}")

# 9. 可视化结果
plt.scatter(X_test, y_test, color='blue', label='真实房价')
plt.plot(X_test, predictions, color='red', label='预测房价')
plt.xlabel('房屋面积')
plt.ylabel('房价')
plt.legend()
plt.show()

大白话解释：

我们用"房屋面积"预测"房价"，就像你看到"房子有多大"，就能猜出"大概多少钱"。

线性回归是机器学习中最简单的模型，但它是理解更复杂模型的基础。

6. 第四阶段：深度学习（3-4个月）

为什么学深度学习？

因为深度学习能处理更复杂的问题（如图像识别、自然语言处理）。

6.1 深度学习核心概念

概念	大白话解释	代码示例
神经网络	模仿人脑的计算结构	`model = Sequential()`
卷积神经网络（CNN）	专门处理图像的神经网络	`Conv2D(32, (3,3), activation='relu')`
循环神经网络（RNN）	专门处理序列数据（如文本）	`LSTM(64)`

6.2 深度学习实战：MNIST手写数字识别

python 复制代码

# 导入必要的库
import tensorflow as tf
from tensorflow.keras import layers, models
import matplotlib.pyplot as plt

# 1. 加载MNIST数据集（手写数字数据集）
(train_images, train_labels), (test_images, test_labels) = tf.keras.datasets.mnist.load_data()

# 2. 数据预处理（归一化）
train_images = train_images / 255.0
test_images = test_images / 255.0

# 3. 构建CNN模型
model = models.Sequential([
    layers.Conv2D(32, (3,3), activation='relu', input_shape=(28,28,1)),
    layers.MaxPooling2D((2,2)),
    layers.Conv2D(64, (3,3), activation='relu'),
    layers.MaxPooling2D((2,2)),
    layers.Flatten(),
    layers.Dense(64, activation='relu'),
    layers.Dense(10, activation='softmax')
])

# 4. 编译模型
model.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])

# 5. 训练模型
history = model.fit(train_images.reshape(-1, 28, 28, 1), train_labels, 
                    epochs=5, 
                    validation_split=0.2)

# 6. 评估模型
test_loss, test_acc = model.evaluate(test_images.reshape(-1, 28, 28, 1), test_labels, verbose=2)
print(f'测试集准确率: {test_acc:.2f}')

# 7. 可视化训练过程
plt.plot(history.history['accuracy'], label='训练准确率')
plt.plot(history.history['val_accuracy'], label='验证准确率')
plt.xlabel('轮次')
plt.ylabel('准确率')
plt.legend()
plt.show()

大白话解释：

我们用CNN（卷积神经网络）识别手写数字。

卷积层：像"扫描仪"一样扫描图片，找出边缘、线条等特征

池化层：压缩特征，减少计算量

全连接层：把特征组合起来，做出最终判断

7. 第五阶段：大模型（3-4个月）

为什么学大模型？

因为大模型是当前AI的最前沿，也是未来5-10年的核心。

7.1 大模型核心概念

概念	大白话解释	代码示例
Transformer	处理序列数据的新型架构	`model = T5Model.from_pretrained('t5-small')`
自注意力机制	模型能"关注"输入中的关键部分	`attention_scores = Q @ K.T / sqrt(d_k)`
提示工程（Prompt Engineering）	通过"提示词"引导模型输出	`prompt = "翻译成英文：你好"`

7.2 大模型实战：用Hugging Face实现文本生成

python 复制代码

# 导入必要的库
from transformers import pipeline

# 1. 加载预训练模型（GPT-2）
generator = pipeline('text-generation', model='gpt2')

# 2. 生成文本
prompt = "今天天气真好，"
output = generator(prompt, max_length=50, num_return_sequences=1)

# 3. 打印结果
print("生成的文本：", output[0]['generated_text'])

大白话解释：

我们用GPT-2模型生成文本。

GPT-2是大模型的一种，能根据提示生成连贯的文本

max_length=50：生成最多50个字

num_return_sequences=1：生成1个结果

8. 经典书目推荐（真正有用的）

书名	作者	适合人群	为什么推荐
《普林斯顿微积分读本》	Adrian Banner	微积分入门	用生活案例讲解极限、导数、积分，适合零基础
《普林斯顿概率论读本》	Steven J. Miller	概率论入门	结合赌徒问题、彩票案例，通俗易懂
《线性代数及其应用》	David C. Lay	线性代数入门	强调矩阵在工程、计算机中的应用
《Introduction to Linear Algebra》	Gilbert Strang	线性代数进阶	MIT经典教材，矩阵分解、特征值讲解清晰
《机器学习》	周志华（西瓜书）	机器学习入门	最全面、最易懂的中文机器学习教材
《深度学习》	Ian Goodfellow（花书）	深度学习入门	深度学习的"圣经"，理论扎实
《动手学深度学习》	阿斯顿·张等	深度学习实践	代码+理论，边学边练
《Hugging Face Transformers》	Hugging Face团队	大模型实践	大模型实战的"官方指南"

9. 附录：数学公式与代码对照表

概念	公式	Python代码示例
导数	f ′ ( x ) = lim ⁡ h → 0 f ( x + h ) − f ( x ) h f'(x) = \lim_{h \to 0} \frac{f(x+h) - f(x)}{h} f′(x)=limh→0hf(x+h)−f(x)	`from sympy import * x = symbols('x'); f = x**2; diff(f, x)`
积分	∫ a b f ( x ) d x \int_a^b f(x) dx ∫abf(x)dx	`from sympy import * x = symbols('x'); f = x**2; integrate(f, (x, 0, 1))`
贝叶斯定理	$P(A	B) = \frac{P(B
矩阵乘法	A × B A \times B A×B	`import numpy as np; A = np.array([[1,2],[3,4]]); B = np.array([[5,6],[7,8]]); np.dot(A, B)`

10. 总结：AI学习不是"学技术"，而是"学思维"

不要只学API，要学原理（为什么这个模型有效？）
不要只看教程，要动手实践（写代码、调模型、跑数据）
不要追求"最新"，要追求"最懂"（先掌握基础，再学前沿）

最后送你一句话 ：

"AI不是魔法，是工程。 "

------ 你不需要成为"AI天才"，只需要系统地学习、持续地实践、真实地解决问题。

【写在最后】

这条学习路径，是我亲自走过的，也是我帮过上百个朋友走过的。
AI不是高不可攀，而是可以一步步学的。

从今天开始，每天学一点，每天做一点，你也能成为AI领域的专业人士。

记住：
不是"我不会"，而是"我还没开始"。
不是"太难了"，而是"我需要更多时间"。

从今天开始，你就是AI学习者。

11. 附：系列博文链接

技术极客小毅：专注于深度学习与AI前沿技术，致力于将复杂的技术用简单易懂的方式分享给读者。欢迎关注我的博客，一起探索AI的无限可能！